基于SHPB实验的挤压AZ91D镁合金动态力学行为数值模拟

周 霞，赵昌美，李 利，黄宏军

(1. 大连理工大学 运载工程与力学学部 工业装备结构分析国家重点实验室，大连 116024;2. 沈阳工业大学 材料科学与工程学院，沈阳 110870)

镁合金由于具有密度低、比强度高、比弹性模量大、散热好、消震性好等优点而被广泛应用于航空航天、汽车、化工等领域[1-3]。AZ91D 镁合金是目前工业上应用最广泛的镁合金之一，在其工作过程中除了承受准静态荷载外，还不可避免地会受到爆炸、冲击等动态荷载的作用，为了更好地分析和设计这些镁合金结构，有必要进一步研究 AZ91D镁合金在动态荷载下的力学行为。

目前，对 AZ91D镁合金力学行为的研究主要集中在对其准静态压缩和拉伸力学性能方面[4-8]，较少涉及由低到高应变速率(1×102~1×103s-1)范围的动态力学行为[9]。对AZ91D镁合金在高应变率时的动态力学行为的研究主要是通过霍普金森杆实验进行的，该实验技术可以宏观地研究镁合金的动态响应及其本构特性、强度特征和破坏机理。沙桂英等[10]和赵峰等[11]研究了AZ91镁合金的动态压缩应力应变行为、应变率效应及其破坏机理，发现镁合金AZ91在高应变率时表现出明显的应变率敏感性，材料动态破坏断口形貌与准静态破坏断口相比也有很大不同；廖慧敏等[12]对 AZ91D压铸镁合金分别进行了静态和动态拉伸实验，研究了不同应变速率对 AZ91D镁合金力学行为的影响规律，并确定了其 Johnson-Cook (J-C)本构关系；GUPTA等[13]使用分离式 SHPB压杆测试方法对AZ91D镁合金在中等应变速率下的压缩力学行为和反复压缩失效机理进行了试验分析，得出在中等应变速率下试样的失效表现为基体开裂和沉积相破碎，这两种失效机理导致试样在初始变形时的高能吸收；AHMAD等[14]对铸造 AZ91D镁合金在应变速率为300~1250 s-1之间的动态拉伸力学行为进行了实验研究，发现AZ91D镁合金在应变速率高于1000 s-1时具有较高的应变速率敏感性，而当应变增大时应变速率敏感性下降。进一步地，AHMAD等[15]对铸造AZ91D镁合金在应变速率为300~1250 s-1之间的动态压缩力学行为进行了实验研究，并与AM50镁合金进行了对比，发现 AZ91D镁合金的应变速率敏感性随着应变率增大先增大后减小，而AM50镁合金在实验范围内具有正应变速率敏感性，同一应变速率时 AZ91D镁合金具有较高的应力。此外，毛萍莉等[16]还对挤压态Mg-Gd-Y 稀土镁合金沿不同方向的动态压缩力学性能与失效行为进行了实验研究，发现随应变速率的提高，该材料具有正应变速率强化效应，沿挤压方向材料的动态压缩性能较好，动态压缩载荷下的断裂呈准解理断裂特征，其变形方式表现为孪生和滑移共同作用。

尽管霍普金森杆实验是描述材料在高应变率下动态力学性能的重要方法，但除了实验测试手段以外,采用数值模拟方法可以较好地再现实验现象、减少实验量, 验证实验获得的相关材料参数[17]。众所周知，同铸造AZ91D镁合金相比，挤压AZ91D镁合金由于晶粒细化和沉积相的均匀分散，其强度和塑性得到很大提高。少数研究者[18-21]对其准静态力学性能和腐蚀性能进行了研究，但有关其动态力学性能的研究还鲜见报道[22]。本文作者采用 ANSYS-LS-DYNA 动力学分析软件，对AZ91D镁合金在3种不同应变速率下沿挤压方向的动态压缩本构行为进行数值模拟，分析镁合金应力的应变速率相关性，探讨Johnson-Cook模型描述一维应力状态下镁合金相关本构关系的可行性，同时与实验对比验证镁合金SHPB实验的有效性。

1 动态压缩力学性能实验及结果

将标准成分的AZ91D合金铸锭先在200 ℃保温时效处理2 h，再在410 ℃固溶处理22 h，然后随炉冷却直到室温，最后将热处理后的样品在 380 ℃时以18.3:1的挤压比和 2.5 mm/s的挤压速度进行热挤压，挤压 AZ91D合金棒材横截面的原始金相显微组织如图1所示，其组织由等轴晶和细小的再结晶晶粒组成，平均晶粒度在10 μm左右。

图1 挤压AZ91D镁合金的显微组织Fig. 1 Microstructure of extruded AZ91D Mg alloy

用线切割从棒材上切取实验压缩试样，试样尺寸分为d8 mm×12 mm和d8 mm×6 mm两种，大尺寸试样用于准静态实验，小尺寸试样用于应变率在400~1000 s-1之间的动态实验。常温准静态实验在Instron材料试验机上进行，准静态压缩试验采用的加载应变率为0.001 s-1。常温动态压缩实验采用霍普金森压杆(SHPB)装置完成(见图 2)，所选实验条件为 3种应变率(440、760及1050 s-1)。上述所有试样的压缩方向都与挤压方向相同，并在进行压缩试验前，需将试样端面打磨光滑，以减少端面与压头的摩擦。

通过上述实验方法，获得的部分不同应变率下的实验结果见图3。其中，试样中的应变率、应变

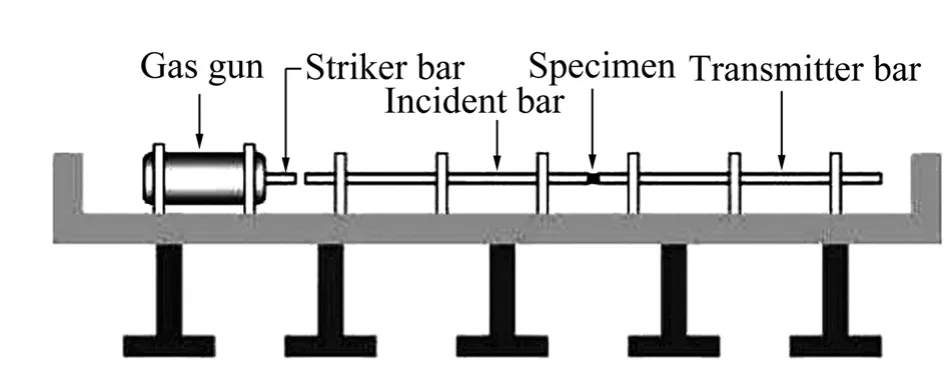
图2 SHPB实验原理图Fig. 2 Schematic diagram of SHPB system

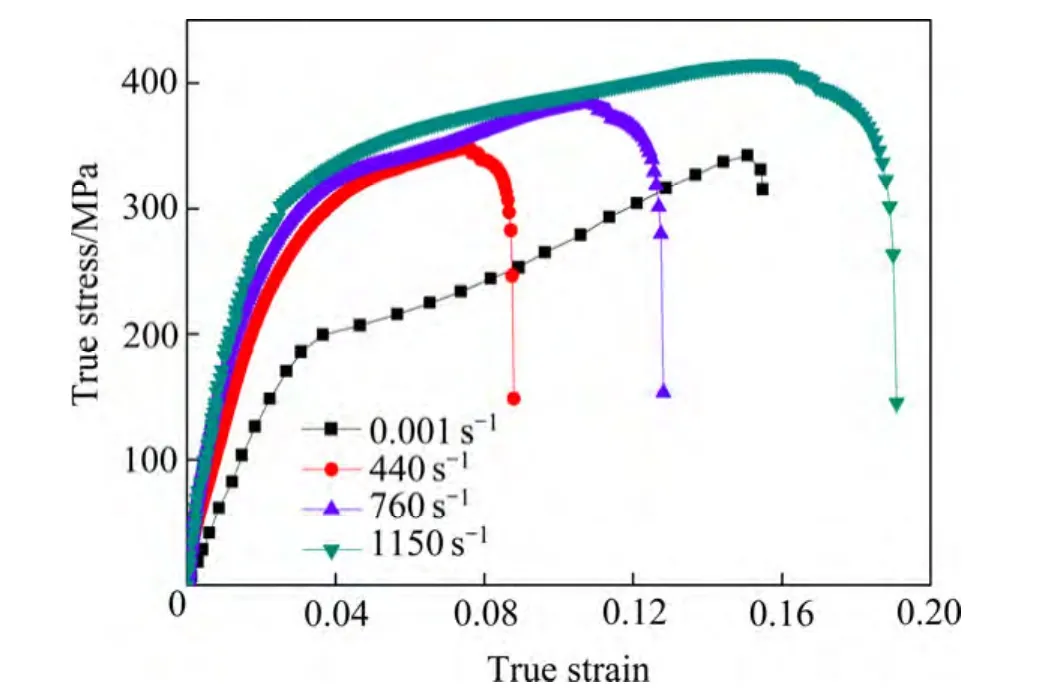
图3 不同应变率下挤压AZ91D合金压缩应力-应变曲线Fig. 3 Stress-strain curves of extruded AZ91D alloy under different strain rates

式中：iε、rε和tε分别为入射杆上和透射杆上应变片测得的应变值；C0为压杆波速；As和ls分别为复合材料试件的横截面积和试验段长度；E和A分别是压杆的弹性模量和横截面积。

由图3可以看到，在实验中由于采用波形整形器，实验获得的应力-应变曲线比较光滑，其动态下的屈服极限最大可达170 MPa。与挤压AZ91D在准静态下的压缩力学性能相比，当应变率由400 s-1至1000 s-1变化时，材料的塑性流变应力呈逐渐上升趋势，且随着应变的增大而增大，该材料在常温下显示出正应变率效应和应变硬化效应，且其在高应变速率下的应力均高于准静态时的应力。

2 Johnson-Cook本构拟合

Johnson-Cook 强度模型的简单形式包含了应变率和温度效应的影响，并且可以对金属材料的本构关系给出比较理想的预测。本文作者尝试在 J-C 强度模型的基础上描述 AZ91D镁合金的常温动态压缩力学行为，J-C 模型表达式如下：

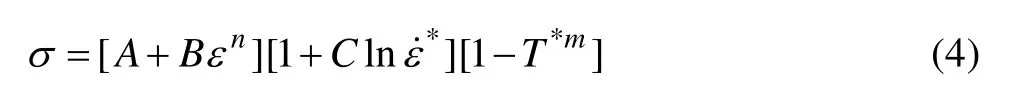
该模型包含了A、B、n、C、m这5个参数，需要通过实验来确定，公式中ε˙*=ε˙/ε˙0是通过参考应变率ε˙0无量纲化的应变率，取ε˙0为1 s-1。T*为无量纲化的温度：式中：Tr为室温；Tm为材料的熔点。Johnson-Cook模型在温度从室温到材料熔点温度的范围内都是有效的。本实验中有限元模拟不考虑温度的影响，即T*值为零。

结合挤压AZ91D镁合金静动态压缩实验下应力-应变曲线的特征，拟合出挤压AZ91D的Johnson-Cook本构关系, 拟合结果见式(6)：

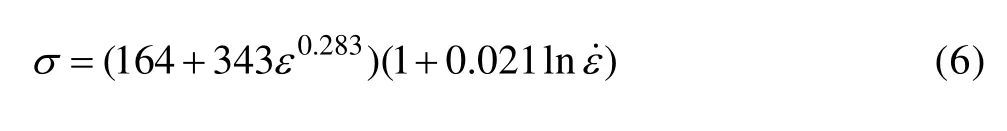
3 SHPB实验的有限元模拟

3.1 有限元模型与网格划分

有限元模型的建立主要参考SHPB实验装置，子弹、入射杆、透射杆、试样均为圆柱体，且共轴。数值模型对设备和试件尺寸进行了简化，子弹长度为 2 cm，入射杆长度为100 cm，透射杆长度为80 cm，子弹、压杆的直径均为2.5 cm，试件长度为1.5 cm，直径为 2 cm。计算单元使用 8节点六面体单元3Dsolid164，该单元可用于三维的显式结构实体，节点在X、Y、Z方向有平移、速度和加速度的自由度。因为系统为对称结构，为了减少计算量，模拟采用1/4有限元模型。采用外圆内方的方式进行网格划分，由于子弹的网格划分精度对计算结果影响很大，故本模拟中对子弹的网格进行了细分，子弹的单元边长为0.67 cm，压杆的单元边长为1 cm，试件单元边长为0.05 cm。图4和图5所示分别为计算几何模型和有限元网格模型，有限元模型单元与节点数如表1所列。

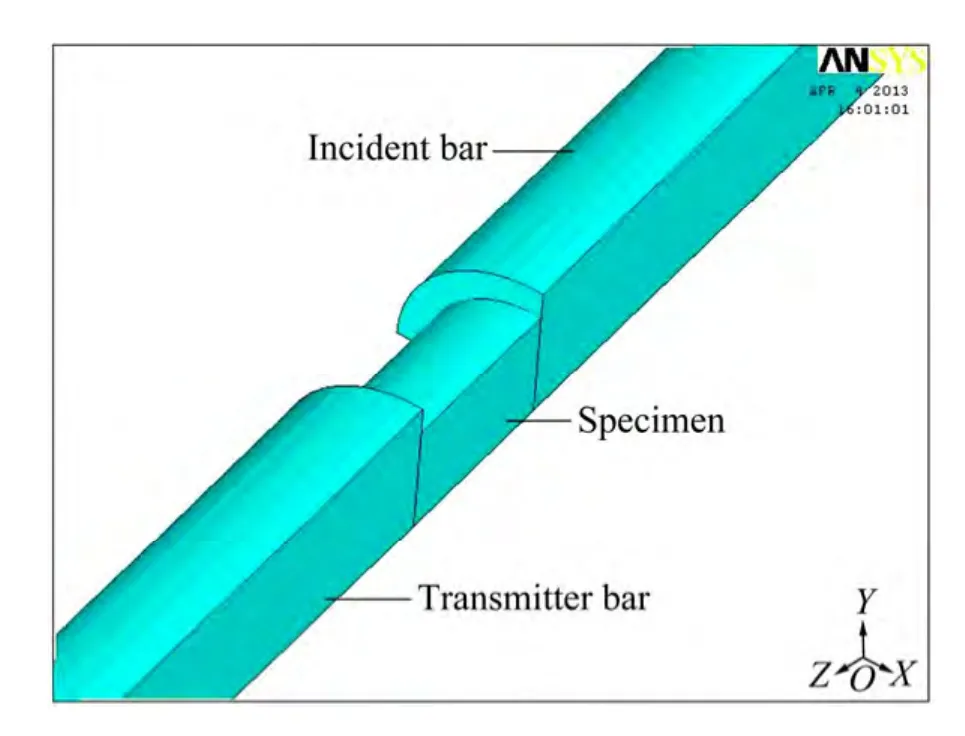
图4 SHPB几何模型图Fig. 4 Geometric model of SHPB

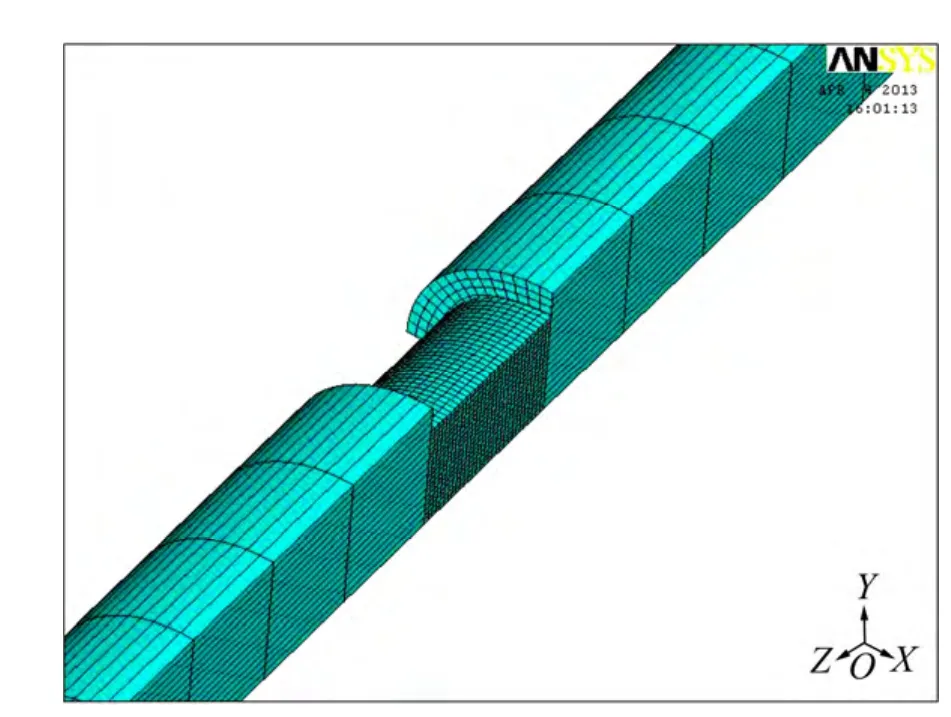
图5 SHPB有限元网格模型Fig. 5 Finite element mesh model of SHPB

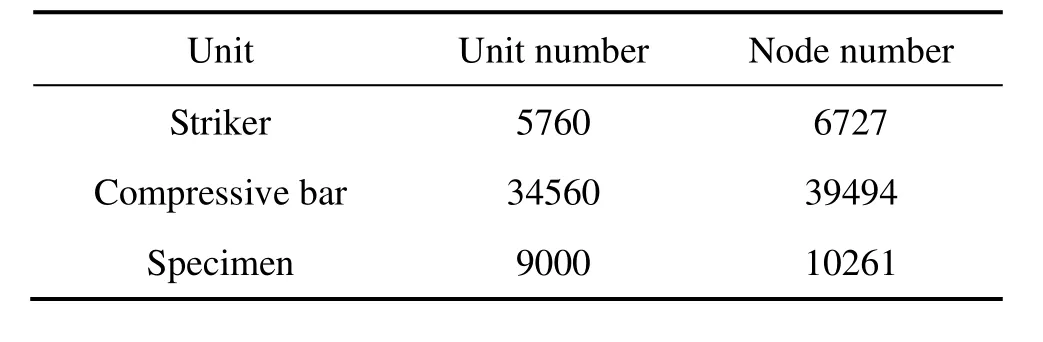
表1 SHPB有限元模型单元及节点数Table 1 Unit and node numbers of finite element model for SHPB

3.2 材料属性和边界条件

子弹和压杆均采用线弹性钢材料模型，其密度为7900 kg/m3，弹性模量为210 GPa，泊松比为0.3，试件采用Johnson-Cook材料模型以及Gruneisem状态方程来描述其动态响应过程。镁合金的密度为 1820 kg/m3，常温下弹性模量为45 GPa，泊松比为0.35，J-C本构参数如表2所示。

表2 AZ91D镁合金的Johnson-Cook (J-C) 本构参数Table 2 Johnson-Cook (J-C) constitutive model parameters for AZ91D magnesium alloy

对于边界条件的设置，与X轴垂直的平面施加X方向的位移约束，与Y轴垂直的平面施加Y方向的位移约束，接触类型选择面面自动接触，忽略各接触面之间的摩擦。依据SHPB试验，采用直接对子弹设定加载速度的方式进行动态模拟。

3.3 数值模拟计算结果与讨论

为了确定计算时间，必须满足入射杆应力波的输入端不能出现入射波和反射波的重叠这一条件[23]，也就是在输入应力脉冲的时间内，应力波的传播距离不能超过两倍的入射杆长度，经过计算应力波的传播时间ts≤400 μs，因此，计算时间取400 μs就可以得到完整的波形图。

选择入射杆中心位置附近的单元(15873)，其入射波与反射波应变波曲线如图6所示。在计算结果的入射杆及透射杆中点附近位置选取对称的两点(15873单元和32873单元)，获得入射波和透射波应变波曲线，如图 7所示。根据该位置处的应变-时间曲线按两波法重构得到镁合金的应力-应变曲线。

当子弹入射速度为10 m/s时，经过计算应变率为440 s-1，在时间t=186 μs左右时，应力波还未到达试件，试件上Mises应力基本为零，如图8所示。在时间t=264 μs时，经过应力波的反射和透射，试件达到均匀变形阶段，其单元上的应力如图9所示。随着应力波在压杆中的扩散，试件进入卸载阶段，如图10 所示。

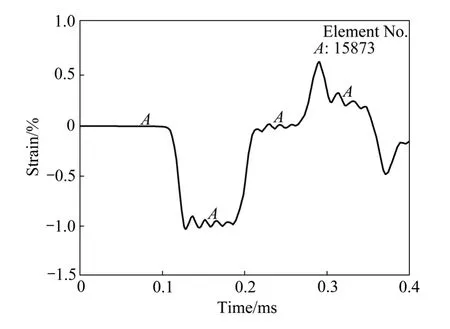
图6 入射杆中心外围单元入射波与反射波Fig. 6 Incident and reflected strain waves at input bar

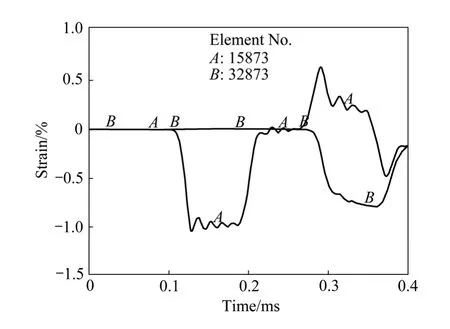
图7 入射杆与透射杆上对称位置单元上的入射与透射波形Fig. 7 Incident and transmitted strain waves at symmetrical units of input and output bars

选择试件上同一横截面上的5个单元(见图11)，其等效应力和应变随时间的变化曲线分别如图 11和图12所示。

按照上述同样的计算方法可以分别计算子弹冲击速度分别为15和20 m/s时试件的动态力学响应，最后根据模拟得到的波形图对不同子弹速度冲击时试件上的应力和应变进行计算便可以得到应力-应变曲线，图13显示了子弹冲击速度分别为10、15及20 m/s或对应应变速率分别为440.7、762.9及1101.4 s-1时试件应力-应变曲线的对比。

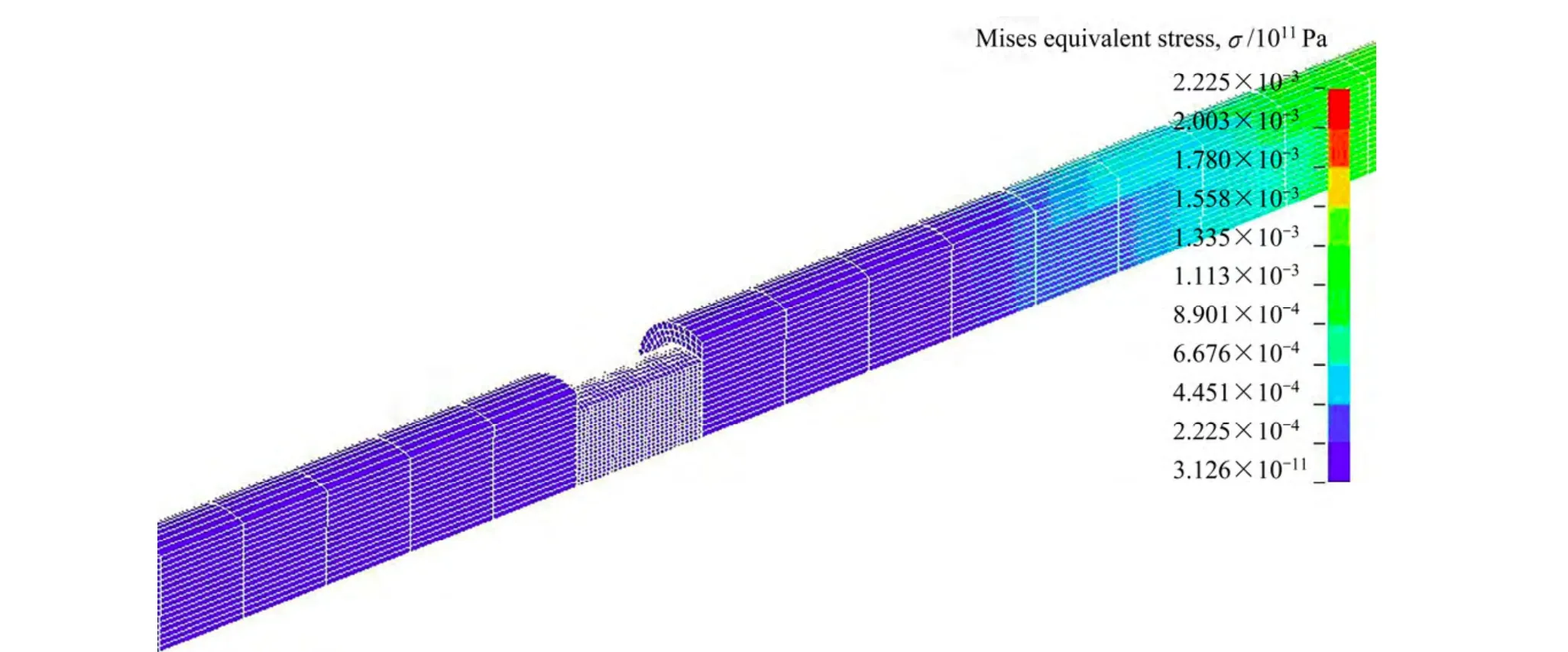
图8 应力波前沿在186 μs到达试件时的Mises等效应力Fig. 8 Mises equivalent stress when stress wave reaching specimen at 186 μs

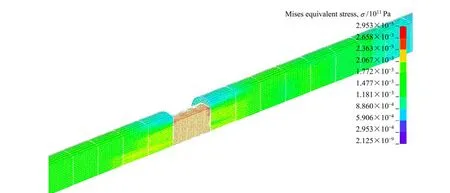
图9 试件在264 μs经历均匀变形时的Mises应力分布Fig. 9 Mises stress distribution after specimen experiencing uniform deformation at 264 μs

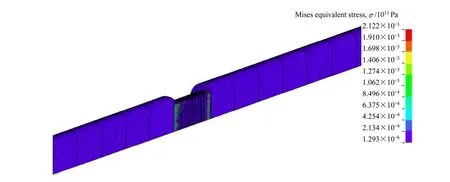
图10 试件在372 μs处于卸载阶段的Mises应力Fig. 10 Mises equivalent stress during unloading period of specimen at 372 μs

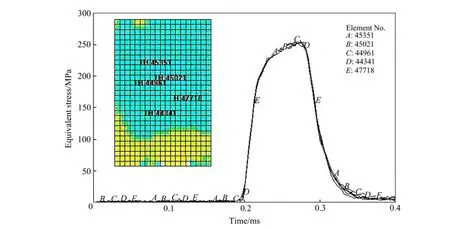
图11 试件上不同单元的应力-时程曲线Fig. 11 Stress vs time curves of different units on specimen

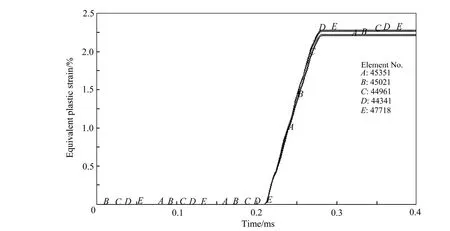
图12 试件上5个单元等效应变随时间的变化曲线Fig. 12 Equivalent strain vs time curves for five units on specimen

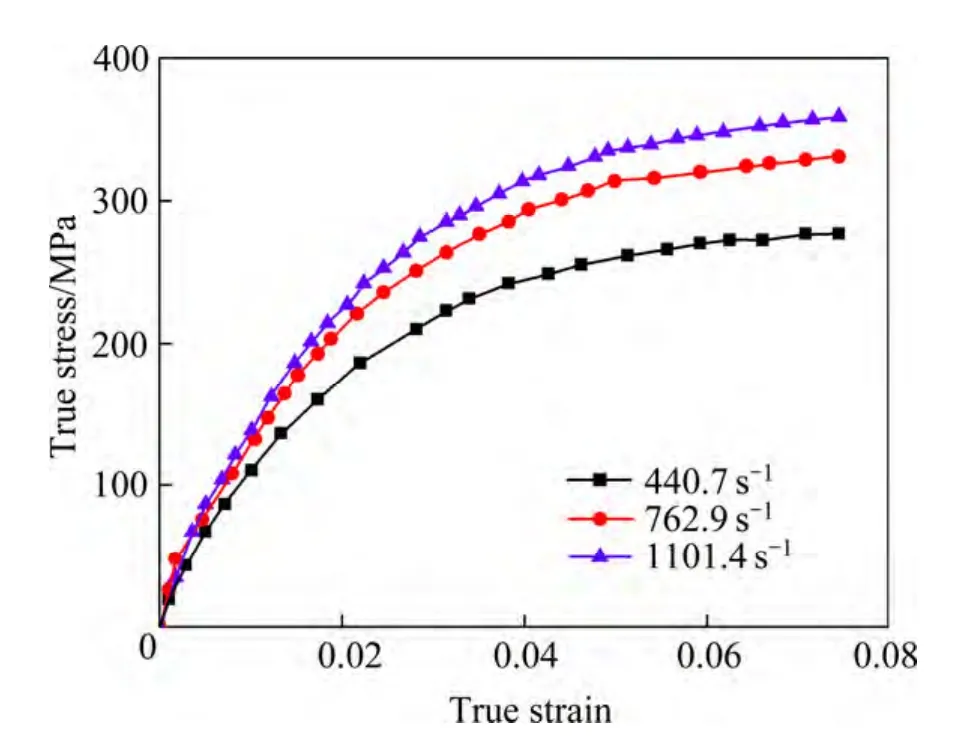
图13 3种应变率下试件的应力-应变曲线Fig. 13 Stress-strain curves for specimen under three kinds of strain rates

应变率对试件的应力-应变曲线有很大影响，应变率越高，试件的变形越大，产生的应力也越大。为了验证数值模拟的有效性，将子弹入射速度为20 m/s即冲击速率为1101.4 s-1时的数值模拟结果、拟合数据及试验结果进行了对比，结果如图14所示。可以看出，使用Johnson-Cook本构模型来模拟挤压AZ91D 镁合金在受到动态压缩荷载时的力学响应是合理的。

从拟合结果来看，在中等应变大小情况下，数值模拟结果与实验结果以及基于 Johnson-Cook 本构模型的拟合结果吻合得较好。但是在应变比较大时，因材料的应变率效应和温度效应耦合在一起，采用解耦的 Johnson-Cook 模型描述材料的应变率效应将会存在一定的不足。

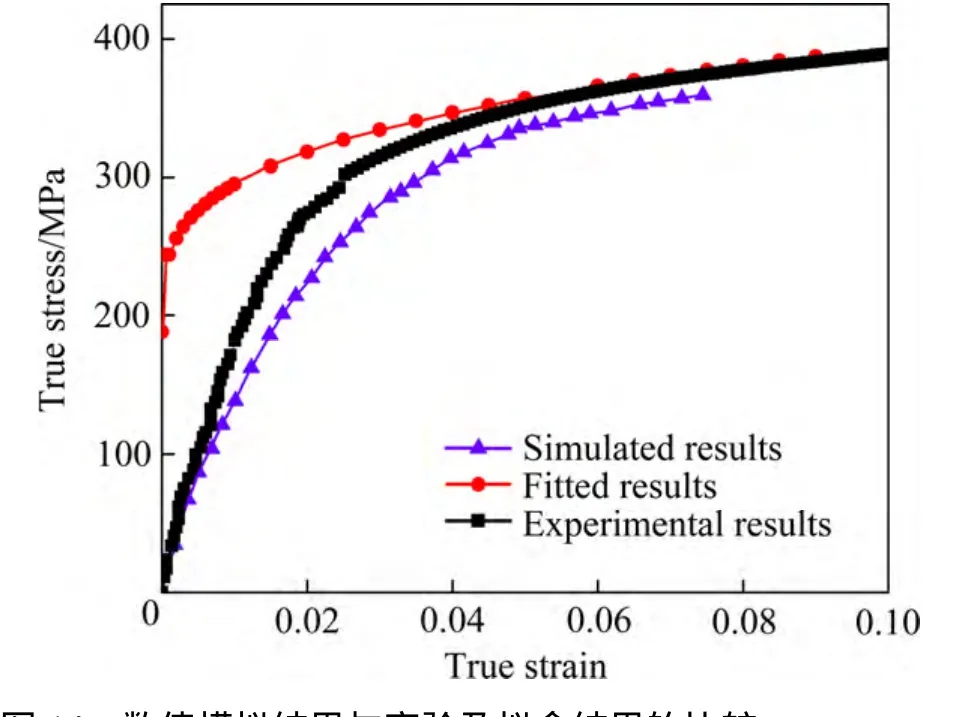
图14 数值模拟结果与实验及拟合结果的比较Fig. 14 Comparison among numerical simulation, experimental and fitted results

4 结论

1) 在 1×10-3~1×103s-1应变率范围内对挤压AZ91D镁合金进行了压缩实验，获得了其在不同应变率下的压缩应力-应变数据，且基于实验拟合了该挤压合金的 Johnson-Cook 本构关系表达式。发现挤压AZ91D 镁合金在室温应变速率条件下，随着应变速率增加表现出较强的应变速率强化效应，其动态塑性流变应力均高于准静态时的应力。挤压镁合金较好的动态压缩性能与镁合金变形后出现拉伸孪晶导致二次硬化有关。

2) 在实验基础上，建立了挤压镁合金试样SHPB压缩实验的有限元模型，模拟分析了应变速率在400~1000 s-1范围内的压缩应力-应变行为，模拟结果、拟合结果与实验结果基本一致，研究结果为金属高应变率力学行为的研究提供了重要的手段和理论指导。

[1] MORDIKE B L, EBERT T. Magnesium: Propertiesapplications-potential[J]. Materials Science and Engineering A,2001, 302(1): 37-45.

[2] HONO K, MENDIS C L, SASAKI T T, OHISHI K. Towards the development of heat treatable high-strength wrought Mg alloys[J]. Scripta Materialia, 2010, 63(7): 710-715.

[3] ISHIHARA S, TANEGUCHI S, SHIBATA H, GOSHIMA T,SAIKI A. Anisotropy of the fatigue behavior of extruded and rolled magnesium alloys[J]. International Journal of Fatigue,2013, 50: 94-100.

[4] LI R G, XU Y, QI W, AN J, LU Y, CAO Z Y, LIU Y B. Effect of Sn on the microstructure and compressive deformation behavior of the AZ91D aging alloy[J]. Materials Characterization, 2008, 59(11): 1643-1649.

[5] KIM B H, LEE S W, PARK Y H, PARK I M. The microstructure, tensile properties, and creep behavior of AZ91,AS52 and TAS652 alloy[J]. Journal of Alloys and Compounds,2010, 493(1/2): 502-506.

[6] MAHMUDI R, KABIRIAN F, NEMATOLLAHI Z.Microstructural stability and high-temperature mechanical properties of AZ91 and AZ91+2RE magnesium alloys[J].Materials & Design, 2011, 32(5): 2583-2589.

[7] NAMI B, RAZAVI H, MIRDAMADI S G, SHABESTARI S G,MIRESMAEILI S M. Effect of Ca and rare earth elements on impression creep properties of AZ91 magnesium alloy[J].Metallurgical and Materials Transactions A, 2010, 41(8):1973-1982.

[8] SHAHZAD M, QURESHI A H, WAQAS H, Rafi-ud-din.Influence of pre- and post-extrusion heat treatments on microstructure and anisotropy of mechanical properties in a Mg-Al-Zn alloy[J]. Materials and Design, 2013, 51: 870-875.

[9] 杨勇彪, 王富耻, 谭成文, 才鸿年. 镁合金动态力学行为研究进展[J]. 兵器材料科学与工程, 2008, 31(3): 71-73.YANG Yong-biao, WANG Fu-chi, TAN Cheng-wen, CAI Hong-nian. Research progress in dynamic mechanical properties of magnesium alloy[J]. Ordnance Material Science and Engineering, 2008, 31(3): 71-73.

[10] 沙桂英, 徐永波, 于 涛, 张修丽, 韩恩厚, 刘 路. AZ91镁合金的动态应力-应变行为及其应变率效应[J]. 材料热处理学报, 2006, 27(4): 77-81.SHA Gui-ying, XU Yong-bo, YU Tao, ZHANG Xiu-li, HAN En-hou, LIU Lu. Dynamic stress-strain behavior of AZ91 magnesium alloy and its dependence on strain rate[J].Transactions of Materials and Heat Treatment, 2006, 27(4):77-81.

[11] 赵 峰, 李玉龙, 索 涛, 黄卫东, 刘建睿. 高应变率下铸造镁合金 AZ91 的动态压缩性能及破坏机理[J]. 中国有色金属学报, 2009, 19(7): 1163-1168.ZHAO Feng, LI Yu-long, SUO Tao, HUANG Wei-dong, LIU Jian-rui. Dynamic compressive behavior and damage mechanism of cast magnesium alloy AZ91[J]. The Chinese Journal of Nonferrous Metals, 2009, 19(7): 1163-1168.

[12] 廖慧敏, 龙思远, 蔡 军. 应变速率对 AZ91D镁合金力学行为影响[J]. 材料科学与工艺, 2010, 18(1): 120-123.LIAO Hui-min, LONG Si-yuan, CAI Jun. Influence of high strain-rate on the mechanical behavior of Mg-alloy AZ91D[J].Materials Science & Technology, 2010, 18(1): 120-123.

[13] GUPTA N, LUONG D D, ROHATGI P K. A method for intermediate strain rate compression testing and study of compressive failure mechanism of Mg-Al-Zn alloy[J]. Journal of Applied Physics, 2011, 109(10): 103512.

[14] AHMAD I R, WEI S D. Mechanical behaviour of magnesium alloy AZ91D using split hopkinson tensile bar (SHTB)[C]// Proc of SPIE. Bellingham: SPIE Press, 2010: 75222C-1-75222C-7.

[15] AHMAD I R, WEI S D. Compressive properties of AM50 and AZ91D alloys using split hopkinson pressure bar[C]// Proc of SPIE, 2009: 7493.

[16] 毛萍莉, 于金程, 刘 正, 董 阳, 席 通. 挤压态 Mg-Gd-Y镁合金动态压缩力学性能与失效行为[J]. 中国有色金属学报,2013, 23(4): 889-897.MAO Ping-li, YU Jin-cheng, LIU Zheng, DONG Yang, XI Tong.Dynamic mechanical property and failure behavior of extruded Mg-Gd-Y alloy under high strain rate compression[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(4): 889-897.

[17] 王焕然, 谢书港, 陈大年, 俞宇颖, 刘国庆. 试论镁铝合金高应变率单轴压缩拟合本构关系的代入校核[J]. 工程力学,2006, 23(9): 179-183.WANG Huan-ran, XIE Shu-gang, CHEN Da-nian, YU Yu-ying,LIU Guo-qing. On the checking of fitted constitutive relation of an Mg-alloy under uniaxial compression at high strain rates[J].Engineering Mechanics, 2006, 23(9): 179-183.

[18] ZHAO Z, CHEN Q, WANG Y, SHU D. Microstructures and mechanical properties of AZ91D alloys with Y addition[J].Materials Science and Engineering A, 2009, 515(1/2): 152-161.

[19] PARAMSOTHY M, CHAN J, KWOK R, GUPTA M. The overall effects of AlN nanoparticle addition to hybrid magnesium alloy AZ91/ZK60A[J]. Journal of Nanotechnology,2012, Article ID 687306, doi:10.1155/2012/687306.

[20] SONG D, MA A, JIANG J, LIN P, YANG D, FAN J. Corrosion behaviour of bulk ultrafine grained AZ91D magnesium alloy fabricated by equal-channel angular pressing[J]. Corrosion Science, 2011, 53(1): 362-373.

[21] 陈永哲, 柴跃生, 孙 钢, 陈 睿, 周俊琪, 张敏刚. AZ91D镁合金棒材挤压过程的数值模拟研究[J]. 精密成形工程,2011, 3(3): 10-14.CHEN Yong-zhe, CHAI Yue-sheng, SUN Gang, CHEN Rui,ZHOU Jun-qi, ZHANG Min-gang. Numerical simulation study of the extrusion process of AZ91D magnesium alloy bar[J].Journal of Net Shape Forming Engineering, 2011, 3(3): 10-14.

[22] SRIVATSAN T S, GODBOLE C, QUICK T, PARAMSOTHY M, GUPTA M. Mechanical behavior of a magnesium alloy nanocomposite under conditions of static tension and dynamic fatigue[J]. Journal of Materials Engineering and Performance,2013, 22(2): 439-453.

[23] LU J F, ZHUANG Z, SHIMAMURA K, SHIBUE T.Application of numerical simulation to SHPB test to investigate the dynamic compressive behavior of material with failure[J].Key Engineering Materials, 2003, 243/244: 433-438.