AZ31镁合金板材冲压成形制耳的晶体塑性模拟

唐伟琴，李大永，彭颖红

(上海交通大学 机械与动力工程学院，上海 200240)

塑性各向异性是造成金属板材冲压制耳现象的主要根源[1]。晶体塑性理论以晶体学织构及其在成形过程中的不断演化作为分析塑性应变问题的基础，比经典塑性理论更忠实于各向异性性能的物理本质，能够更好地预测金属板材冲压制耳行为。随着计算机技术的发展，晶体塑性理论已被广泛应用于模拟金属板材的冲压成形过程。董湘怀课题组[2-4]开发了相关晶体塑性模型，研究了不同初始织构对面心立方结构(FCC)板材深冲成形制耳的影响。NAKAMACHI等[5-6]利用弹-黏塑性有限单元方法成功模拟了体心立方结构(BCC)板材深冲时的4个和6个制耳现象。KIM等[7]、ENGLER 等[8]、耿小亮等[9]和李大永等[10]分别将晶体塑性本构模型与有限元相结合，研究FCC、BCC金属板材冲压成形过程中的织构演化及其对制耳的影响。

然而，目前晶体塑性理论在冲压成形制耳方面的应用大都集中在立方结构(FCC和BCC)金属，其主要塑性变形机制为滑移，且滑移系和滑移方向确定。镁合金为密排六方结构(HCP)，主要滑移系有基面滑移、柱面滑移、锥面滑移和锥面滑移，中常温下孪生也是协调c轴方向应变的主要机制。孪生为单向切变机制，其激活不仅与加载方向有关，而且还与变形温度、合金成分和晶格结构等密切相关，使得滑移与孪生的相互作用十分复杂[11]。AL-SAMMAN等[12]和HUANG等[13]分别对不同织构的镁合金进行了平面应变压缩实验和拉深实验，结果表明，不同的初始织构将导致塑性变形过程中启动的变形机制不同。近年来，基于晶体塑性模型模拟镁合金的变形行为及其在变形过程中的织构特性得到越来越多的关注。对于镁合金多晶体模拟，主要采用基于Taylor模型的模拟[14-16]和基于自洽模型(Self consistent, SC)的模拟[17-20]两种方法。Taylor模型比较简单，数值上容易实现，但是该模型没有考虑晶粒间的相互作用，不能描述变形过程中由于各向异性引起的变形不均匀现象[21]。自洽模型在处理孪生的问题上具有物理意义上的优势，至今已发展成为弹塑性自洽模型(Elastic-plastic self-consistent, EPSC)、黏塑性自洽模型(Viscoplastic self-consistent, VPSC)和弹黏塑性自洽模型(Elastic-viscoplastic self-consistent, EVPSC)，适用于小变形、大变形、蠕变行为等多种变形条件，但是当本构模型比较复杂时，需要反复迭代求解应力-应变关系，计算过程繁杂[22]。另一种方法是将晶体塑性模型与商用有限元软件(如ABAQUS)结合，即采用晶体塑性有限元(Crystal plasticity finite element method,CPFEM)对镁合金的塑性变形过程进行模拟[23-25]，该方法为解决复杂边界条件下的织构特性及对宏观力学行为的影响提供了有效途径。镁合金变形机制的多样性和不确定性，以及冲压过程本身的复杂性，使得从晶体塑性理论角度预测镁合金的冲压成形比立方结构金属复杂得多。目前，仅WALDE等[23]建立了黏塑性自洽多晶体本构模型(VPSC)，并嵌入 ABAQUS有限元对镁合金冲压过程进行了模拟，但是该模型假设初始织构为简单的理想织构，如(0°, 0°, 0°)或(0°, 90°,0°)，没有对实际轧制镁板的冲压性能进行研究。

本文作者首先将滑移主导的晶体塑性理论扩展到耦合滑移、孪生的晶体塑性理论，建立适合密排六方金属的晶体塑性本构模型；在此基础上，构建镁合金板材大变形晶体塑性有限元模型，预测AZ31轧制板材的杯形件冲压制耳行为，并对该预测方法进行试验验证。

1 密排六方单晶体塑性模型

1.1 滑移与孪生的耦合方法

建立 HCP晶体塑性本构模型主要是要解决滑移与孪生的耦合方法，而滑移和孪生两种变形方式耦合的关键问题是确定孪生对塑性应变的贡献以及孪生引起的晶体转动。

1.1.1 孪生对塑性应变的贡献

由于孪晶的极性，所以孪生只能沿着孪晶方向进行。本模拟中假定孪生为特定的滑移系，将塑性应变增量 Δ εp分解为孪生和滑移变形两部分的加权平均，单个晶粒的塑性应变增量表达式如下[26]：

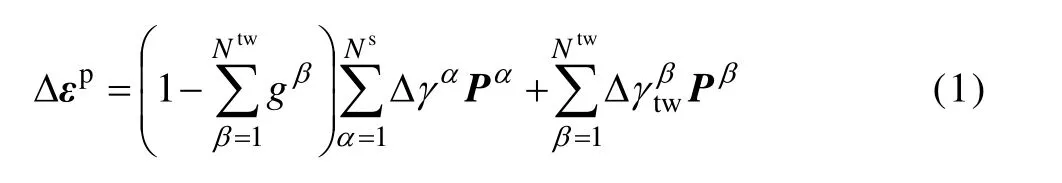
式中：∑ gβ为孪晶体积分数，Ns和 Ntw分别为开动滑移系和孪晶系的数目，Δ γα和分别为滑移系和孪晶系的剪切应变增量，采用TAKAHASHI等[27]提出的应变速率无关的“连续迭代法”求解，P为Schmid张量，它根据滑移面法向n和滑移方向m定义如下：

1.1.2 孪生引起的晶体转动

孪生导致晶体转动的模式与滑移不同，本文作者采用主导孪晶旋转(PTR)模型[28]，即根据占主导地位的孪晶系来计算孪生对于晶体转动的贡献。计算步骤归纳如下。

在每一个变形步，第n个晶粒第β个孪晶系的孪晶体积分数增量为

对所有晶粒、所有孪晶系进行求和得到总的孪晶分数(FR)：

式中：n

f为晶粒n的体积分数。对所有已发生孪晶旋

转的晶粒进行求和得到有效孪晶分数(FE)：

孪生引起旋转的临界值定义为

式中：A1、A2是材料常数。在每一个变形步里，若最活跃的孪晶系的累积孪晶分数β,ng 超过临界值TF，则整个晶粒就根据该孪晶系的取向进行旋转，同时将已发生旋转的孪晶分数加入有效孪晶分数。

根据下式更新发生孪晶旋转的取向：

式中：R和R′分别为发生孪晶旋转前后的晶体旋转矩阵；Rtw为孪晶与母体的旋转关系；n为孪晶切变方向。

1.2 单晶体本构方程

首先考虑单晶体的变形，现时构型即t+Δt时刻的Cauchy应力为

应力增量σΔ由材料本构关系确定：

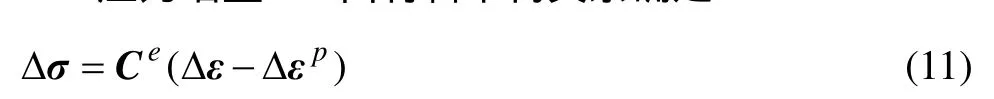
式中： Ce为4阶弹性张量；总应变增量Δε可由宏观变形转换得到，塑性应变增量 Δ εp由式(1)计算得到。

1.3 开动滑移/孪生系的确定

判断滑移/孪生系是否开动，即判定某一晶粒是发生滑移变形还是孪生变形，是计算晶体塑性变形的前提。根据拉伸实验，晶体滑移/孪生系能否开动取决于拉应力在滑移/孪生系上的切应力分量的大小。第α滑移/孪生系上的剪切应力为

根据 Schmid临界切应力定律：切应力分量达到临界值是滑移/孪生系处于塑性屈服状态的必要条件。但是临界滑移/孪晶系并非一定是活动滑移/孪晶系，塑性流动的产生不仅要求滑移/孪生系处于临界状态，而且要求一致性条件得到满足。因此，滑移/孪生系是否开动可由以下条件进行判断：

1.4 硬化模型

式中：N为晶体滑移系的数目；αβh 为硬化模量，表

示滑移系β中的滑移剪切应变对滑移系α所产生的硬化，可表示为

式中：αβ

q 为描述自硬化和潜在硬化行为的矩阵，可表示为

式中：q为通过潜在硬化实验确定的潜在硬化与自硬化的比值。δαβ为Kronecher符号。hα可以通过求解：

1.5 晶体取向的确定

晶体在塑性变形过程中的取向转动导致织构演化，它由两部分组成：晶格旋转和孪生引起的晶体转动，后者根据式(8)和(9)进行求解，而晶格旋转引起的取向变化为

式中：R为发生晶格旋转前的晶体旋转矩阵，Δω*为晶格旋转增量，可由下式计算：

式中：Δω为总体旋转增量，可由宏观变形转换得到，Δωp为塑性旋转增量，可由下式求解：

式中：W为Schmid张量，它根据滑移面法向n和滑移方向m定义如下：

2 镁合金多晶体塑性模型

HCP多晶体模型主要有泰勒模型、自洽模型和有限单元模型(Finite element model, FEM)。文献[29]通过对比模型单元数及每个单元代表晶粒数的不同组合分析得出如下结论：只要总的晶粒个数(单元个数和每个单元代表的晶粒个数的乘积)达到一定数量，就可以获得比较稳定的统计结果；该文献也指出耦合有限元的弹塑性自洽模型比较耗时。泰勒模型虽然简单，但将孪生作为一个连续体，与实际情况不相符合，对孪生进行模拟时需采取一些特殊处理手段，如考虑晶界滑移等晶间相互作用，以提高模拟精度。因此，本模拟中采用有限元方法耦合晶体塑性模拟镁合金板材大变形，其中每个单元代表一个晶粒，因为用有限单元方法模拟多晶体能够同时满足相容条件和平衡条件，而无需泰勒或自洽多晶体假设，降低了对计算机的性能要求，模拟精度也得到了保证。

镁作为 HCP金属，塑性变形时启动的滑移/孪生系组合及其各自的临界剪切应力(CRSS)存在不确定性及复杂性，并且随着合金成分及温度的变化而不同[11,15]，因此，对于给定的镁合金材料及变形温度，变形机制及模型参数的确定是建立晶体塑性有限元模型的关键。

本文作者基于以上 HCP单晶体塑性模型编制了用户材料子程序，嵌入到 ABAQUS有限元中，根据各变形机制的特性及镁板变形过程中的织构演化特征确定微观变形机制，通过拟合拉伸或压缩变形的应力-应变曲线及各向异性参数r值获得模型参数，从而建立了AZ31板材大变形晶体塑性有限元模型。

AZ31轧制板材的织构如图 1所示，初始织构为大部分晶粒c轴平行于板材法向的基面织构。在进行有限元模拟时将测得的反映该织构的一组欧拉角(Φ1,Φ,Φ2)作为镁板多晶体初始取向赋给各个晶粒。

2.1 变形机制的确定

对于纯镁，可启动的变形机制有基面滑移，柱面滑移，锥面滑移，锥面滑移和拉伸孪生[28]，如图2所示。

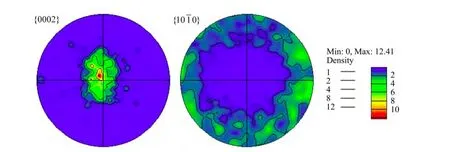
图1 AZ31镁合金轧制板材的初始织构Fig. 1 Initial texture of hot rolled magnesium alloy sheet: {0001} and {1 010} pole figures

图2 镁合金的主要变形机制Fig. 2 Main slip/twinning systems in magnesium alloy: (a) Basal slip; (b) Prismatic slip; (c) Pyramidal slip;(d) Pyramidal slip; (e) Tensile twinning

由拉伸孪生启动条件及AZ31板材的初始织构可知：当沿着镁板平面内任何方向进行拉伸时，拉伸孪晶处于硬取向而几乎不能启动，因此，晶粒c轴方向的变形只能由锥面滑移来协调，即锥面滑移在拉伸变形过程中必不可少；基面滑移的CRSS比其他滑移系的小很多，在变形过程中通常都会启动；根据文献[19, 30]可知，镁合金板材单向拉伸后转变为{0 001}〈10 1 0〉单一织构，而柱面滑移是导致镁板该织构形成的因素。

鉴于此，本文作者将AZ31板材150 ℃变形时的变形机制取为基面滑移、柱面滑移、锥面滑移和拉伸孪生。此处没有考虑锥面滑移，因为锥面滑移引起的变形和织构演化可由基面滑移和柱面滑移组合作用代替。

2.2 模型参数的拟合

镁合金作为各向异性材料，硬化参数的拟合须同时满足各个方向的应力-应变曲线和表征塑性各向异性特征的塑性应变比r值。本模拟中分别沿着轧向(RD)、45°方向、横向(TD) 3个方向进行单轴拉伸或压缩，根据拉伸方向8%的伸长量计算塑性应变比r值，计算公式如下：

式中：lε、wε和tε分别为长度、宽度和厚度方向的塑性应变。

由于AZ31板材沿着面内单向拉伸时拉伸孪生不启动，所以一方面可排除孪生的作用而先确定滑移系的参数，从而使得问题简化；另一方面，孪生的参数无法根据面内单向拉伸来确定，本文作者根据沿 RD方向压缩来确定，由于实验条件的限制，该实验值由文献[19]获得。

以沿RD方向拉伸和压缩为例，图3所示为实验测试和模拟计算的应力-应变曲线。由图3可知，AZ31轧制板材除了平面各向异性外，还显示了拉压不对称性，这是由于变形孪晶将引起进一步滑移/孪生的变形阻力，该效应通过设置潜在硬化系数(表1中“Latent”)来体现。图4显示了镁板沿RD、45°、TD这3个方向拉伸变形过程中的r值演化，其中曲线为模拟结果，3个数据点为应变0.08时对应的实验结果。由图可知，沿3个方向加载时r值均随着应变的增加而增大；应变为0.08时，模拟所得的r值与实验测试值趋势一致，即r值从RD到TD方向逐渐增大。表1所列为拟合得到的多晶体模型的硬化系数。

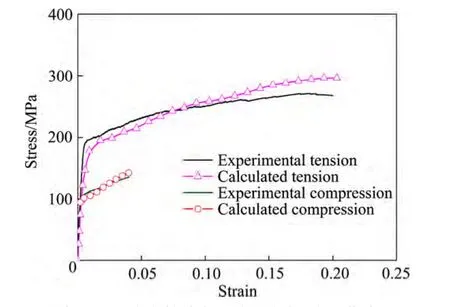
图3 镁板沿RD方向拉伸和压缩的应力-应变曲线Fig. 3 Simulated stress-strain curves for tension or compression along RD together with experimental measurements

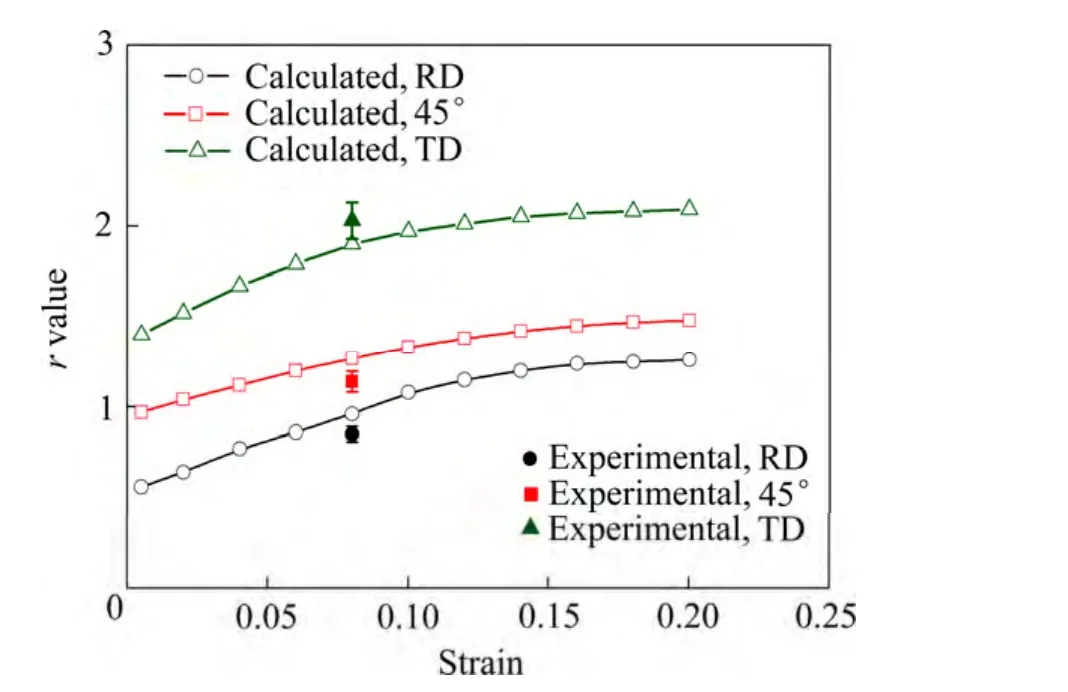
图4 镁板拉伸变形过程中r值的变化Fig. 4 Simulated evolution of r value during tension together with experimental measurements

表1 AZ31板材多晶体模型的硬化系数Table 1 Hardening coefficients for polycrystal model of AZ31 Mg alloy sheet

3 AZ31镁板的冲压制耳行为

3.1 制耳行为的模拟与分析

图5所示为杯形件冲压成形示意图，模型几何尺寸如表2所列。板材采用两层C3D8R单元，冲头、压边圈、凹模都定义为解析刚体，冲压件与冲头、压边圈、凹模之间的摩擦因数均为0.1，所用压边力为5 kN。将测得的AZ31板材的一组欧拉角(Φ1,Φ,Φ2)通过VUMAT子程序赋给各个晶粒，作为有限元模型的初始输入条件。

图5 杯形件冲压成形示意图Fig. 5 Geometric sketch for deep cup drawing tools of AZ31 Mg alloy (Dp—Punch diameter; Dd—Die diameter; Rp—Round radius of punch; Rd—Round radius of die; Db—Sheet diameter;tb—Sheet thickness)

表2 冲压模具尺寸Table 2 Dimensions for cylindrical cup drawing tools (mm)

根据冲压过程及冲压件性能可知，杯底的变形几乎可忽略，其微观组织和织构与初始轧板相似，本模拟中仅考虑杯壁的织构变化情况。对 AZ31板材在150 ℃条件下杯形件冲压进行有限元仿真，冲压行程为30 mm。图6所示为AZ31板材冲压杯形件模拟结果。从图 6(a)可以看出，杯形件呈现出显著的偏离轧向45°制耳，图6(b)显示出显著的(0 001)〈10 1 0〉织构组分和拉伸孪晶组分。

不同变形机制对变形的贡献按下式来计算：

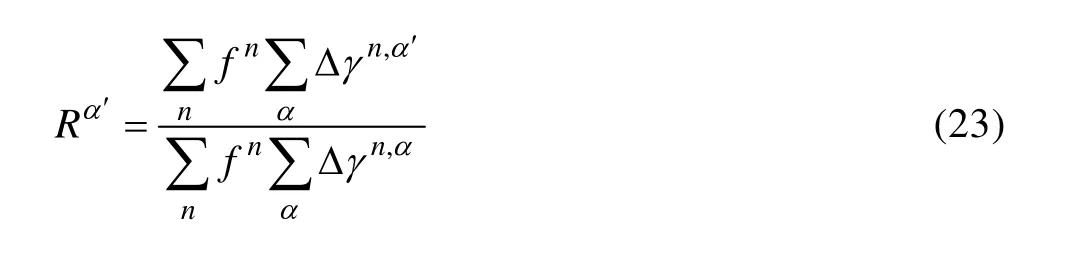
图6 AZ31板材150 ℃冲压杯形件模拟结果Fig. 6 Simulation results for deep-drawn cup of AZ31 alloy sheet formed at 150 ℃: (a) Earing profiles; (b) Pole figures

式中：fn表示第n个晶粒的体积分数； Δγn,α表示第n个晶粒中第α个滑移/孪生系上的剪切应变增量；α′表示所要计算的各个变形机制；α表示考虑的所有的变形机制。计算结果如图7所示。可以看出，冲压初始阶段拉伸孪生是主要的变形机制，柱面滑移也启动，随着

孪生的进行，晶粒转到易滑移方向，基面滑移和锥面滑移也变得活跃。

图7 150 ℃冲压过程中各种变形机制的相对活动率Fig. 7 Relative activity of each deformation mode as function of strain during deep drawing at 150 ℃

3.2 制耳行为的试验验证

对AZ31板材在150 ℃条件下进行杯形件冲压实验，所得冲压件如图8所示，图中箭头所示方向为轧制方向。冲压件呈现出显著的45°方向制耳。

图8 AZ31板材150 ℃冲压杯形件实验结果Fig. 8 Experimental results for deep-drawn cup of AZ31 alloy sheet formed at 150 ℃: (a) Photo of bottom; (b) Whole photo

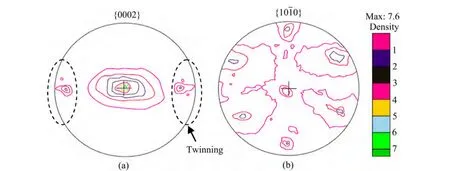
图9 冲压杯形件的织构分布实验结果Fig. 9 Measured texture for deep-drawn cups of AZ31 alloy sheet: (a) {0001} pole figures; (b){1010}pole figures

图9所示为杯形件织构的测试结果，极图中显示了拉伸孪晶织构组分的大量存在，如图 9(a)中虚线部分所示。拉伸孪生主要是由沿圆周的压应变引起的，因为AZ31板材的初始织构为大部分晶粒c轴平行于板厚方向，当沿着圆周进行压缩时，板厚增加，即提供了板厚方向的拉应力，从而晶粒c轴受拉，满足拉伸孪生启动的条件。此外，图 9同样显示出了(0 001)〈10 1 0〉织构组分，该织构组分的形成可归结为柱面滑移的启动。

综上所述，模拟所得的冲压杯形件制耳轮廓和变形织构均与实验结果吻合得较好。

4 结论

1) 建立了耦合滑移和孪生的晶体塑性有限元模型，该模型同时满足各个方向的力学性能曲线和表征塑性各向异性特征的塑性应变比r值，充分体现了镁合金板材与织构相关的各向异性性能。

2) 基于所开发的晶体塑性有限元模型对AZ31板材冲压成形过程进行有限元模拟，模拟的杯形件制耳轮廓和变形织构均与实验结果具有较好的一致性。

[1] 毛卫民. 金属材料的晶体学织构与各向异性[M]. 北京: 科学出版社, 2002.MAO Wei-min. Crystallographic texture and anisotropy of metals[M]. Beijing: Science Press, 2002.

[2] 郑 莹, 董湘怀, 李志刚. 晶体方位对钣料成形制耳的影响[J]. 中国机械工程, 2001, 12(9): 1070-1072.ZHENG Ying, DONG Xiang-huai, LI Zhi-gang. The effect of crystal orientation on earing in sheet metal forming[J]. China Mechanical Engineering, 2001, 12(9): 1070-1072.

[3] 章海明, 董湘怀. 一种适用于率相关晶体塑性模型的准隐式积分算法[J]. 精密成形工程, 2011, 3(6): 1-5.ZHANG Hai-ming, DONG Xiang-huai. An semi-implicit integration scheme for rate dependent crystal plasticity[J].Journal of Netshape Forming Engineering, 2011, 3(6): 1-5.

[4] ZHANG H M, DONG X H, WANG Q, ZENG Z. An effective semi-implicit integration scheme for rate dependent crystal plasticity using explicit finite element codes[J]. Computational Materials Science, 2012, 54: 208-218.

[5] NAKAMACHI E, XIE C L, HARIMOTO M. Drawability assessment of BCC steel sheet by using elastic/crystalline viscoplastic finite element analyses[J]. International Journal of Mechanical Sciences, 2001, 43(3): 631-652.

[6] XIE C L, NAKAMACHI E. Investigations of the formability of BCC steel sheets by using crystalline plasticity finite element analysis[J]. Materials & Design, 2002, 23(1): 59-68.

[7] KIM E Y, CHOI S H, SHIN E J, YOON J W. Simulation of earing behaviors in bake hardening steel exhibiting a strong off-γ-fiber component[J]. International Journal of Solids and Structures, 2012, 49(25): 3573-3581.

[8] ENGLER O, HIRSCH J. Polycrystal-plasticity simulation of six and eight ears in deep-drawn aluminum cups[J]. Materials Science and Engineering A, 2007, 452/453(15): 640-651.

[9] 耿小亮, 张克实, 郭运强, 秦 亮. 非均质材料微成形过程的晶体塑性模拟[J]. 材料科学与工艺, 2010, 18(3): 297-301.GENG Xiao-liang, ZHANG Ke-shi, GUO Yun-qiang, QIN Liang.Crystal plasticity simulation study on the micro-forming of heterogeneous materials[J]. Materials Science & Technology,2010, 18(3): 297-301.

[10] 李大永, 张少睿, 彭颖红, 刘守荣, 仇素萍. 板材冲压成形的晶体塑性有限元模拟[J]. 机械工程学报, 2008, 44(1): 190-194.LI Da-yong, ZHANG Shao-rui, PENG Ying-hong, LIU Shou-rong, QIU Su-ping. Finite element simulation of sheet metal stamping with polycrystalline plasticity[J]. Chinese Journal of Mechanical Engineering, 2008, 44(1): 190-194.

[11] PRANTIL V C, JENKINS J T, DAWSON P R. Modeling deformation induced textures in titanium using analytical solutions for constrained single crystal response[J]. Journal of the Mechanics and Physics of Solids, 1995, 43: 1283-1302.

[12] AL-SAMMAN T, GOTTSTEIN G. Room temperature formability of a magnesium AZ31 alloy: Examining the role of texture on the deformation mechanisms[J]. Materials Science and Engineering A, 2008, 488: 406-414.

[13] HUANG X, SUZUKI K, CHINO Y, MABUCHI M. Influence of initial texture on cold deep drawability of Mg-3Al-1Zn alloy sheets[J]. Materials Science and Engineering A, 2013, 565:359-372.

[14] STYCZYNSKI A, HARTIG CH, BOHLEN J, LETZIG D. Cold rolling textures in AZ31 wrought magnesium alloy[J]. Scripta Materialia, 2004, 50(7): 943-947.

[15] STYCZYNSKI A, HARTIG CH, BOHLEN J, LETZIG D. Cold rolling textures in AZ31 wrought magnesium alloy[J]. Scripta Materialia, 2004, 50(7): 943-947.

[16] LÉVESQUE J, INAL K, NEALE K W, MISHRA R K.Numerical modeling of formability of extruded magnesium alloy tubes[J]. International Journal of Plasticity, 2010, 26(1): 65-83.

[17] CLAUSEN B, TOMÉ C N, BROWN D W, AGNEW S R.Reorientation and stress relaxation due to twinning: Modeling and experimental characterization of Mg[J]. Acta Materialia,2008, 56(11): 2456-2468.

[18] HUANG S, ZHANG S, LI D, PENG Y. Modeling texture evolution during rolling process of AZ31 magnesium alloy with elasto-plastic self consistent model[J]. Transactions of Nonferrous Metals Society of China, 2011, 21: 1348-1354.

[19] AGNEW S R, DUYGULU Ö. Plastic anisotropy and the role of non-basal slip in magnesium alloy AZ31B[J]. International Journal of Plasticity, 2005, 21(6): 1161-1193.

[20] WANG H, WU P D, TOMÉ C N, HUANG Y. A finite strain elastic-viscoplastic self-consistent model for polycrystalline materials[J]. Journal of the Mechanics and Physics of Solids,2010, 58(4): 594-612.

[21] POLMEAR I J. Magnesium alloys and applications[J]. Materials Science and Technology, 1994, 10(1): 1-16.

[22] 王 娜, 雷丽萍, 方 刚, 曾 攀. 镁合金变形的晶体塑性有限元分析[J]. 稀有金属, 2008, 32(6): 766-773.WANG Na, LEI Li-ping, FANG Gang, ZENG Pan. Deformation analysis of magnesium alloy based on crystal plasticity theory[J].Chinese Journal of Rare Metals, 2008, 32(6): 766-773.

[23] WALDE T, RIEDEL H. Simulation of earing during deep drawing of magnesium alloy AZ31[J]. Acta Materialia, 2007,55(3): 867-874.

[24] CHOI S H, KIM D H, LEE H W, SHIN E J. Simulation of texture evolution and macroscopic properties in Mg alloys using the crystal plasticity finite element method[J]. Materials Science and Engineering A, 2010, 527(4/5): 1151-1159.

[25] HUANG S, ZHANG S, LI D, PENG Y. Simulation of texture evolution during plastic deformation of FCC, BCC and HCP structured crystals with crystal plasticity based finite element method[J]. Transactions of Nonferrous Metals Society of China,2011, 21: 1817-1825.

[26] WANG X M, XU B X, YUE Z F. Micromechanical modelling of the effect of plastic deformation on the mechanical behaviour in pseudoelastic shape memory alloys[J]. International Journal of Plasticity, 2008, 24(8): 1307-1332.

[27] TAKAHASHI H, MOTOHASHI H, TOKUDA M, ABE T.Elastic-plastic finite element polycrystal model[J]. International Journal of Plasticity, 1994, 10(1): 63-80.

[28] YI S B, DAVIES C H J, BROKMEIER H G, BOLMARO R E,KAINER K U, HOMEYER J. Deformation and texture evolution in AZ31 magnesium alloy during uniaxial loading[J]. Acta Materialia, 2006, 54(2): 549-562.

[29] 黄诗尧. AZ31镁合金挤压成形微观组织演化的试验研究与数值模拟[D]. 上海: 上海交通大学, 2010.HUANG Shi-yao. Numerial and experimental research on the microstructure evolution of magnesium alloy AZ31 during extrusion process[D]. Shanghai: Shanghai Jiao Tong University,2010.

[30] DEL VALLE J A, RUANO O A. Effect of annealing treatments on the anisotropy of a magnesium alloy sheet processed by severe rolling[J]. Materials Letters, 2009, 63(17): 1551-1554.