Mg-2Al合金的高温拉伸性能和变形机制

乔 军，边福勃，何 敏

(辽宁科技大学 材料与冶金学院，鞍山 114051)

镁合金具有质轻、比强度和比刚度高、导热和导电性好、电磁屏蔽性强、易回收等优异性能，成为航空、汽车、通讯电子等领域，特别是汽车工业构件的优选材料[1-2]。然而，镁合金为密排六方晶体结构，室温变形条件下的滑移系少，塑性低且变形困难，这已成为阻碍镁合金板材深加工的瓶颈问题。因此，近年来关于镁合金高温变形行为尤其是高温超塑性的研究已成为国内外学者的研究热点。镁合金获得超塑性的传统方法主要是细化晶粒，使平均晶粒尺寸小于 10 μm，并利用晶界滑移机制获得超塑性，即细晶超塑性。然而，细晶超塑性不仅需要特殊的冶金和加工工艺来细化晶粒，而且通常以较慢的速度变形，因此增加了生产成本并降低了生产效率。研究发现，平均晶粒尺寸大于10 μm的镁合金也有可能呈现超塑性。例如，刘满平等[3]研究了晶粒尺寸为37.5 μm的AZ31镁合金在温度623~723 K和应变速率1×10-5~1×10-3s-1范围内的超塑性行为，发现该合金的最高伸长率达到314%。因此，近几年来针对粗晶粒镁合金的超塑性研究得到了广泛关注。一般认为，在粗晶粒镁合金的高温变形中，晶界滑移对应变的贡献较小，而晶粒内部的位错运动对应变的贡献较大，因此，变形机制也更为复杂，涉及非基面滑移系的热激活、位错蠕变、动态再结晶等机制。ITO等[4]发现粗晶粒Mg-2.7Al(摩尔分数，%)和 Mg-4.5Al(摩尔分数，%)合金的伸长率大于 250%，并指出非基面滑移系在高温下的启动起到了重要作用。WU等[5]和BLANDIN等[6]研究发现，粗晶粒AZ31和AZ91合金在适当温度和应变速率条件下的伸长率大于 100%，并认为位错蠕变发挥了主要作用。位错蠕变主要包括溶质牵制位错蠕变和位错攀移蠕变。溶质牵制位错蠕变常见于合金中，是指固溶于基体中的溶质原子基于尺寸效应在位错的应力场中形成原子气团，并对位错滑移产生牵制作用，使位错发生黏性滑动，从而使材料呈现较低的应力指数(n≈3)和较高的应变速率敏感性指数(m,m=1/n)，并延缓颈缩发生和提高塑性，蠕变激活能为溶质原子在基体中的扩散激活能[7]。位错攀移蠕变是指应变速率由位错攀移控制的蠕变过程，常见于纯金属或无溶质牵制作用的合金，应力指数较高，n约为 5~8，蠕变激活能为基体原子的自扩散激活能[8]。

粗晶粒 AZ系(Mg-Al-Zn)镁合金具有超塑性，其中Al是最重要的合金添加元素，具有提高强度和增强溶液流动性等作用。然而，溶质Al原子对高温变形机制的影响，尤其是对位错蠕变的影响尚不明确。以往研究多选用AZ系商业镁合金，溶质Al原子的作用易受其他杂质元素的干扰而难以明确。因此，本文作者针对实验室制备的粗晶粒Mg-2Al合金，利用拉伸至失效实验和变化应变速率拉伸实验研究高温拉伸性能，通过计算应力指数和激活能分析变形机制，并与纯Mg对比，研究溶质Al原子对高温变形性能和机制的影响。

1 实验

本研究中Mg-2Al合金(质量分数，%)是以99.98%高纯Mg和99.99%高纯Al为原料，在电阻炉中进行熔炼而得。在熔炼过程中采用了 RJ-2作为保护剂，以防止镁合金发生氧化和燃烧。熔炼后在厚壁铁铸模中浇铸成圆柱状铸锭，利用刨床和线切割机加工成厚度为20 mm、直径为85 mm的圆饼状铸锭。然后加热到400 ℃左右进行多道次的热轧，得到3 mm厚的板材。在400 ℃进行10 h的均匀化热处理后，沿轧制方向切取高温拉伸试验的试样，形状与几何尺寸如图 1所示。

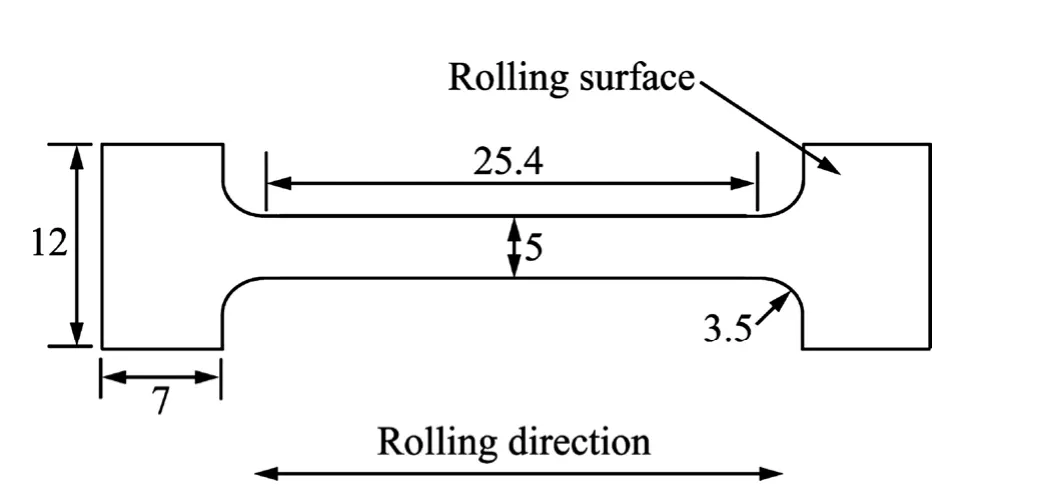
图1 高温拉伸试样的几何尺寸及形状Fig. 1 Dimension of specimen for high temperature tensile test (Unit: mm)

利用SUNS公司的UTM-5305电子万能试验机进行了高温拉伸试验，即拉伸至失效(Elongation-to-Failure, EF)实验和变化应变速率 (Strain-rate-change,SRC)实验。在EF实验中，分别在300、350、400和450 ℃下，以恒定拉伸速率1×10-2和1×10-3s-1拉伸试样至断裂，以断裂后的变形区长度减去初始变形区的长度，再除以初始变形区的长度求得伸长率。在SRC实验中，分别在300、350、400和450 ℃下，将试样在 4.98×10-5~2.02×10-2s-1的应变速率范围进行拉伸。首先，对试样进行30 min的低速率预拉伸变形，使拉伸系统处于稳定状态，且该速率下的显微组织趋于稳定。然后，连续进行9个阶段的应变速率递增的拉伸，在每一阶段以恒定拉伸速率进行一定的变形。利用每一阶段的稳定变形区末端的力和位移数据计算真实应力和真实应变速率，用于计算应力指数和蠕变激活能，并分析变形机制。

为观察 Mg-2Al合金板材在轧制后(热处理前)和热处理后的显微组织，将材料沿轧制方向制成金相试样，经机械研磨和抛光后，用苦味酸(5 g)、乙酸(25 mL)、酒精(100 mL)和去离子水(10 mL)的混合液腐蚀，之后利用JVC TK-350EG光学显微镜观察显微组织，其结果如图2所示。热处理前的平均晶粒尺寸为18.87 μm，热处理后晶粒发生长大，平均晶粒尺寸为48.35 μm。

图2 Mg-2Al合金板材的金相照片Fig. 2 Optical micrographs of Mg-2Al alloy sheet: (a) Before heat treatment; (b) After heat treatment

2 结果与分析

2.1 拉伸至失效(EF)实验

在不同温度下Mg-2Al合金的EF实验的真应力-真应变曲线如图 3所示，其中图 3(a)的拉伸速度为0.0254 cm/s，换算为拉伸速率为ε˙=(0.0254 cm/s)/(2.54 cm)=1×10-2s-1，图 3(b)的拉伸速率为 1×10-3s-1。在每个拉伸速率下，合金的峰值应力均随着温度的增加而降低，稳态变形区域和伸长率均随温度升高而增大。试样在300和350 ℃屈服后呈现明显的强化现象，这是由于屈服后位错运动并发生缠结，但回复和再结晶在较低的变形温度下作用有限。在400和450 ℃则明显不同，出现较长的稳态变形区。

图4所示为经EF实验后Mg-2Al合金的试样对比照片。当ε˙=1×10-2s-1，伸长率均低于 100%(见图4(a))。当ε˙=1×10-3s-1，在各温度下的伸长率均有所提高，在400 ℃和450 ℃下的伸长率均超过100%，在450 ℃达到最高值，为179.5%(见图4(b))。

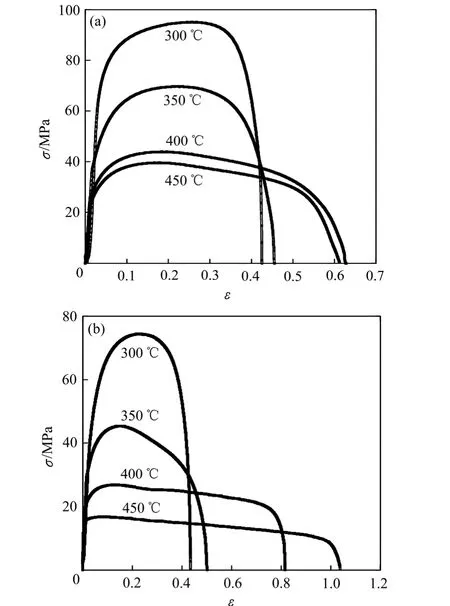
图3 不同温度下Mg-2Al合金的EF实验的真应力-真应变曲线Fig. 3 Stress-strain curves of elongation-to-failure test for Mg-2Al alloy at different temperatures and tensile rates: (a)ε˙=1×10-2 s-1; (b) ε˙=1×10-3 s-1

图4 经EF实验后的Mg-2Al合金试样照片Fig. 4 Photos of Mg-2Al alloy specimens after elongation-tofailure test: (a) ε˙=1×10-2 s-1; (b) ε˙=1×10-3 s-1

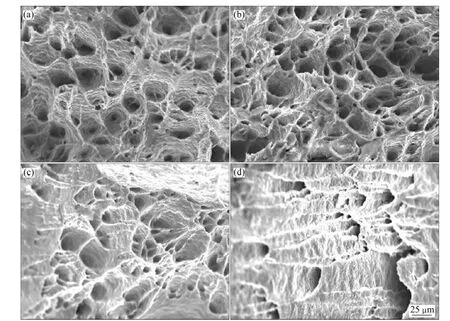
图5 拉伸速率为1×10-2 s-1时EF实验后Mg-2Al合金的断口形貌Fig. 5 Fracture morphologies of Mg-2Al alloy after EF test at 1×10-2 s-1 and different temperatures: (a) 300 ℃; (b) 350 ℃;(c) 400 ℃; (d) 450 ℃

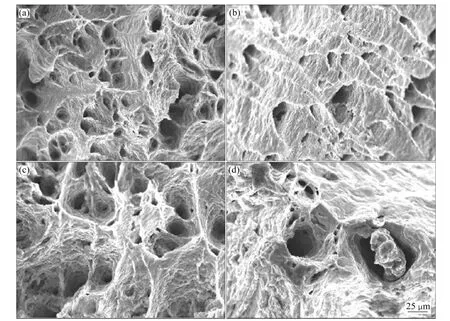
图6 拉伸速率为1×10-3 s-1时EF实验后Mg-2Al合金的断口形貌Fig. 6 Fracture morphologies of Mg-2Al alloy after EF test at 1×10-3 s-1 and different temperatures: (a) 300 ℃; (b) 350 ℃;(c) 400 ℃; (d) 450 ℃

图5和6所示分别为Mg-2Al合金在拉伸速率分别为ε˙=1×10-2s-1和ε˙=1×10-3s-1下 EF 实验后断口的SEM像。断口总体呈韧窝状，且韧窝边有撕裂棱，是典型的沿晶韧性断裂[9]。此外，随着温度的升高，原子扩散能力增强，在应变较大的断口处出现了空洞长大和相互连接现象(见图 5(c)、(d)和图 6(c)、(d))。空洞长大和相互连接会使试样横截面上的受力面积减小和应力增加。因此，图 4中，Mg-2Al合金在450 ℃的伸长率比400 ℃低的现象可能与空洞演变的剧烈程度有关。

2.2 变化应变速率(SRC)实验

金属材料的蠕变主要由应变速率、蠕变应力、晶粒尺寸和变形温度等因素影响，一般遵循如下本构关系[10]：

式中：ε˙为真实应变速率；A为只与材料本身特性有关的常数；G为剪切模量；b为柏氏矢量；k为波尔兹曼常量；T为绝对温度；σ为真实应力；E为弹性模量；n为应力指数；d为晶粒度；p为晶粒度指数(粗晶粒p=0)；D为扩散系数，D=D0exp[-Q/(RT)]，其中D0为指前因子，Q为蠕变激活能，R为摩尔气体常数。

为对比分析溶质Al原子对高温变形机制的影响，对纯Mg也做了相同实验条件下的SRC拉伸实验。图7所示为根据Mg-2Al合金和纯Mg的SRC实验数据在对数坐标中做出的真实应变速率和弹性模量归一化应力曲线，其线性关系说明应变速率和流变应力呈幂律关系。然而与图 7(a)中的纯 Mg不同，图 7(b)中Mg-2Al曲线的斜率随着应变速率的增加而增大，且呈偏离线性关系的趋势，即幂律失效现象。表1所列为利用线性回归计算得到的Mg和Mg-2Al在不同温度下的应力指数n。当温度由300 ℃升高到450 ℃时，Mg的应力指数由5.9降低到5.1，Mg-2Al的应力指数由9.0降低到4.7，变化更为显著，说明溶质Al对高温变形机制产生了较为重要的影响。

2.3 高温变形机制

为进一步研究材料在不同温度和应变速率下的变形行为，引入扩散系数补偿的真实应变速率，即D/ε˙。ROBINSON 等[11]认为有效扩散系数(Effective diffusion coefficient，Deff)适于描述以位错攀移蠕变为主要机制的合金或纯金属中的扩散过程。Deff包括晶格扩散系数(Lattice diffusion coefficient)DL和管扩散系数(Pipe diffusion coefficient)Dp的共同作用，即

式中：DL和Dp的值列于表2中。

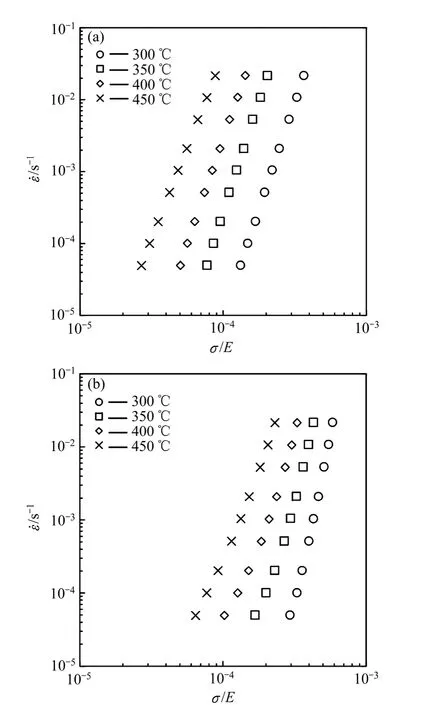
图7 纯Mg和Mg-2Al合金的SRC拉伸实验的真实应变速率与弹性模量补偿的真实应力Fig. 7 True strain rate versus modulus-compensated flow stress in SRC tensile tests for pure Mg(a) and Mg-2Al(b)

表1 不同温度下的应力指数n值Table 1 Calculated stress exponents n at different temperatures

将式(2)代入式(1)进行补偿后，得到如图8所示的ε˙/{Deff[kT/(Gb)]}-σ/G曲线，图中还包含Mg-Al-Zn合金[12]和纯镁[13-14]在不同变形温度(200~350 ℃)下的数据。虽然各种材料在高温和低温变形中的激活能、剪切模量和应力不同，但是应力指数基本接近于n=5，因此变形机制可能为典型的位错攀移蠕变。然而，由表1和图7可知，随着温度升高，Mg-2Al的应力指数降低，并呈现偏离线性关系的趋势，其变形机制可能与纯Mg的有所不同。纯金属的高温变形以位错攀移蠕变为主，而固溶体合金在高温变形中则可能发生溶质牵制蠕变。因此，分别将图7中纯Mg和Mg-2Al的应变速率用Mg的自扩散系数Dsd和Al原子在Mg基体中的扩散系数Dsol补偿(Dsd和Dsol的值见表 2)，得到如图9所示的ED//σε-˙关系曲线。

表2 纯镁的扩散系数Table 2 Diffusion coefficients of pure Mg

图 8 由 SRC实验数据得出的有效扩散系数补偿的真实应变速率和剪切模量补偿的真实应力Fig. 8 SRC test data plotted as strain rate compensated by effective diffusion coefficient versus flow stress compensated by modulus (Data of other work on AZ31, AZ61, AZ91[12] and pure Mg[13-14] are included)

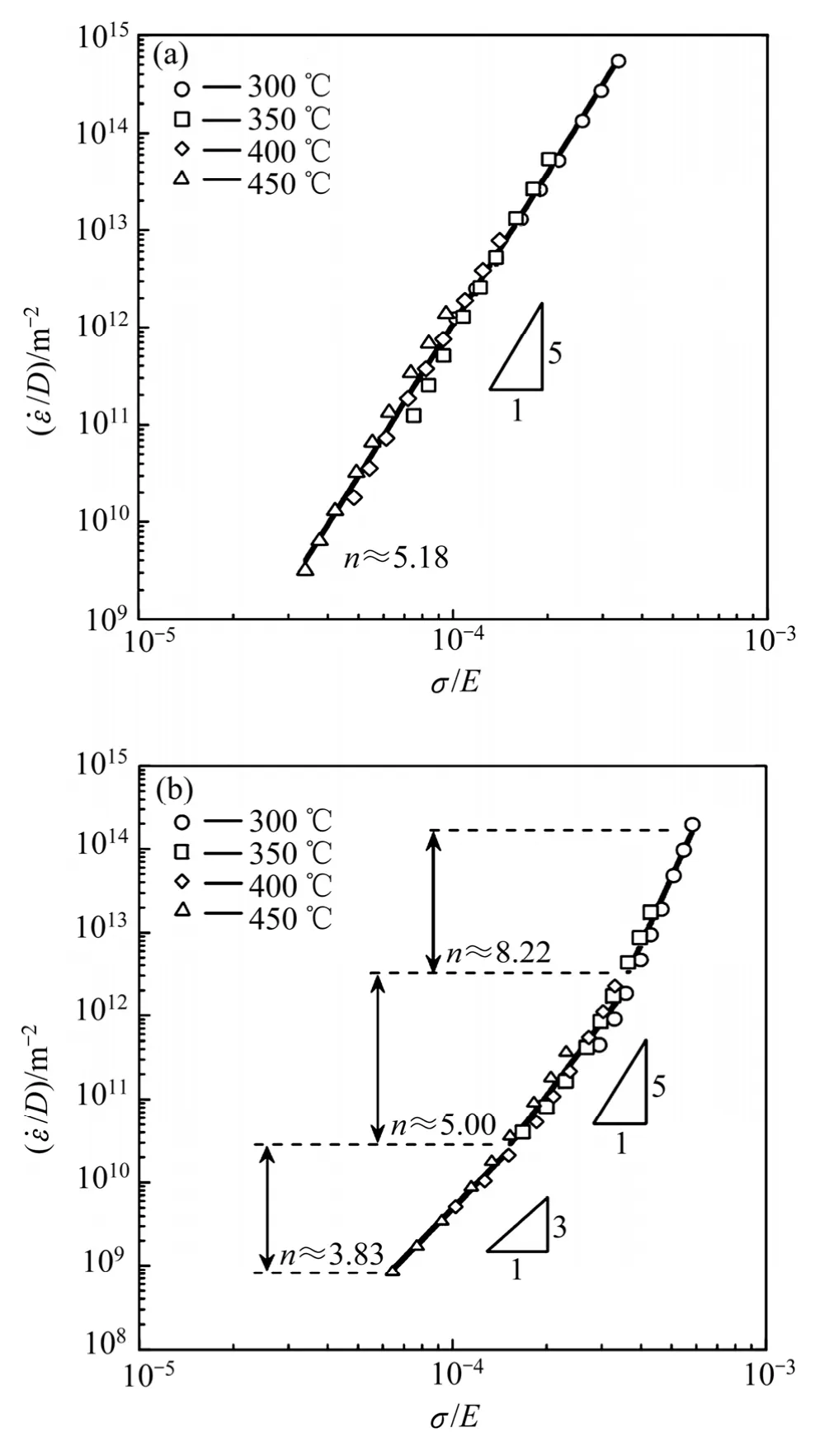
图 9 由 SRC实验数据得出的扩散系数补偿的真实应变速率和弹性模量补偿的真实应力Fig. 9 SRC test data plotted as diffusivity-compensated true strain rate versus modulus-compensated flow stress: (a) Pure Mg; (b) Mg-2Al

如图9(a)所示，纯Mg呈现了较好的线性关系，应力指数为n≈5.18，表明在所采用的SRC实验条件下具有稳定的变形机制，即位错攀移蠕变。相反地，如图9(b)所示，Mg-2Al的应力指数发生明显变化，说明添加2%Al使纯Mg的变形机制发生了改变。根据应力指数的不同将曲线分为3个阶段，即n≈3.83时的高温和低应变速率阶段、n≈5时的中间阶段和n≈8.22时的低温和高应变速率阶段。在Mg-Al固溶体合金的高温变形中，基于使弹性应变能降低的尺寸效应，在适当的温度和应变速率条件下铝原子可在刃位错处形成溶质气团，并与位错应力场发生弹性交互作用。当溶质原子的扩散速率低于位错滑移速率，溶质对位错滑移产生牵制力，使位错发生黏性滑移且速率降低。位错的滑移和攀移是顺序过程。如滑移速率低至一定程度时，则成为变形的主要控制因素，即变形机制由位错攀移蠕变转变为溶质牵制位错蠕变，相应的应力指数由n约为5~8变为n≈3.83，而变形激活能应由Mg原子自扩散激活能转变为溶质Al原子在Mg基体中的扩散激活能[12]。

材料的蠕变激活能公式[18]，

根据式(3)绘制斜率k值计算曲线，如图10所示，横坐标为温度的倒数，纵坐标为EF实验的峰值应力σ的对数，σln。在EF实验中，当拉伸速率为1×10-3s-1、且温度为300 ℃时，稳态流变区间很小，故只计算350、400和450 ℃下的数据，得出k≈ 4.41。

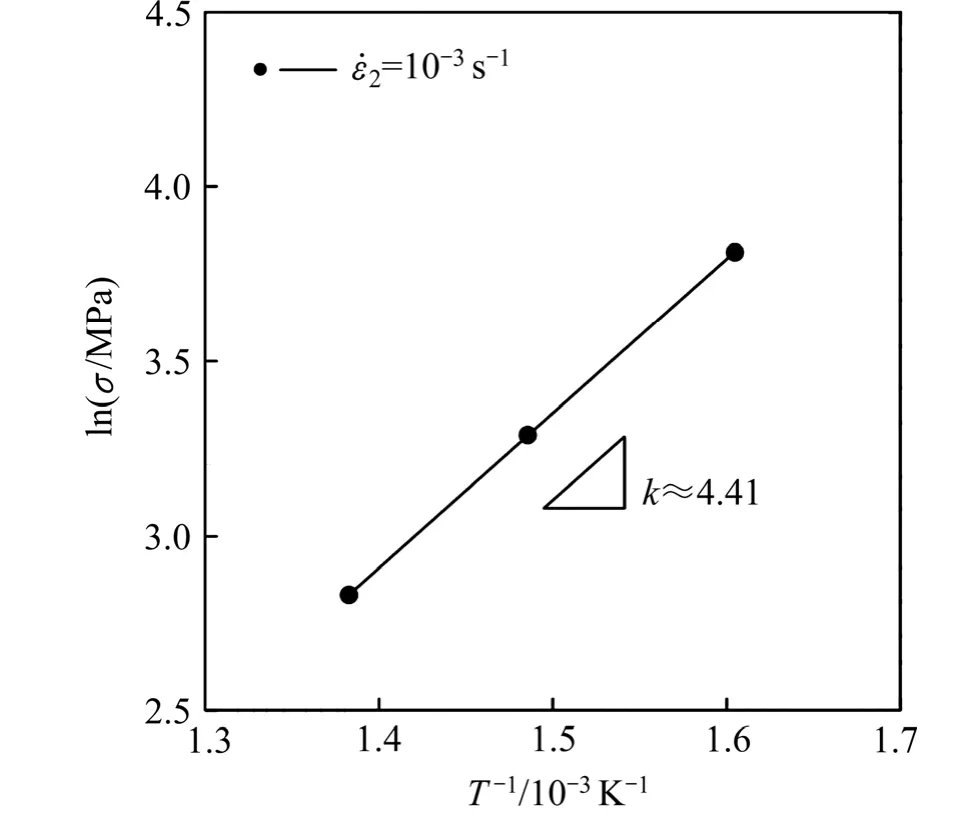
图10 蠕变激活能公式中的k值计算Fig. 10 Calculation of k value in equation of creep activation energy

如图4(b)中的EF实验数据所示，在高温(400和450 ℃)和低拉伸速率(1×10-3s-1)下获得了超过100%的伸长率，即D/ε˙的范围约为8.84×108~2.11×1010m-2，属于图 9(b)中的n≈3.83阶段。因此，将n≈3.8和k≈4.41代入式(3)中，计算得出蠕变激活能为141.46 kJ/mol，接近于溶质原子Al在Mg基体中的扩散激活能，Qsol=(143 ±10) kJ/mol[19]。

因此，综合对应力指数和蠕变激活能的分析，添加2%的Al可使纯Mg的变形机制由位错攀移蠕变向溶质牵制位错蠕变转变。在高温和低拉伸速率的 EF实验条件下，溶质Al原子对于粗晶粒Mg-2Al合金的应力指数的降低和呈现超过 100%的高伸长率起到了重要作用。

3 结论

1) 在所采用的实验条件下，粗晶粒纯Mg只有一种变形机制，即应力指数为n≈5的位错攀移蠕变。

2) 在所采用的实验条件下，粗晶粒Mg-2Al合金中溶质 Al使变形机制由位错攀移蠕变向溶质牵制位错蠕变发生了转变，呈现n≈3.83时的高温和低应变速率阶段、n≈5时的中间阶段和n≈8.22时的低温和高应变速率阶段。在n≈3.83的高温(400和450 ℃)和低拉伸速率(1×10-3s-1)条件下，Mg-2Al的伸长率超过100%，激活能为141.46 kJ/mol，接近于Al在Mg基体中的扩散激活能。

3) 粗晶粒Mg-2Al合金在300和350 ℃屈服后呈现明显的强化现象，在400和450 ℃则呈现了较长区间的稳态变形和较大的断裂伸长率，高温断口为韧窝状韧性断裂，且随着温度的升高，出现了空洞和相互连接。

[1] 李 轶, 程培元, 华 林. 镁合金在汽车工业和 3C产品中的应用[J]. 江西有色冶金, 2007, 21(2): 30-33.LI Yi, CHENG Pei-yuan, HUA Lin. Current application of magnesium alloy in automotive industry and 3C product fields[J].Jiangxi Nonferrous Metals, 2007, 21(2): 30-33.

[2] YU Kun, RUI Shou-tai, SONG Jue-min, LI Wen-xian, GUO Long. Effects of grain refinement on mechanical properties and microstructures of AZ31 alloy[J]. Transactions of Nonferrous Metals Society of China, 2008, 18(S1): s39-s43.

[3] 刘满平, 马春江, 王渠东, 吴国华, 朱燕萍, 丁文江. 工业态AZ31 镁合金的超塑性变形行为[J]. 中国有色金属学报, 2002,12(4): 797-801.LIU Man-ping, MA Chun-jiang, WANG Qu-dong, WU Guo-hua,ZHU Yan-ping, DING Wen-jiang. Superplastic deformation behavior of commercial magnesium alloy AZ31[J]. The Chinese Journal of Nonferrous Metals, 2002, 12(4): 797-801.

[4] ITO T, SAEKI J, OTSUKA M. Superplastic-like behavior in coarse grained Mg-Al solid solutions[J]. Journal-Japan Institute of Metals, 2003, 67(2): 85-92.

[5] WU Xin, LIU Yi. Superplasticity of coarse-grained magnesium alloy[J]. Scripta Materialia, 2002, 46(4): 269-274.

[6] BLANDIN J J, GIUNCHI D, SUERY M. Effect of thermal treatments on mechanical behavior of thixoformed magnesium alloy[J]. Materials Science and Technology, 2002, 18(2):333-340.

[7] WATANABE H, TSUTSUI H, MUKAI T. Deformation mechanism in a coarse-grained Mg-Al-Zn alloy at elevated temperatures[J]. International Journal of Plasticity, 2001, 17(3):387-397.

[8] SPIGARELLI S, CABIBBO M, EVANGELISTA E. Analysis of the creep behavior of a thixoformed AZ91 magnesium alloy[J].Materials Science and Engineering A, 2000, 289(1): 172-181.

[9] 陈洪美, KANG Suk-bong, 于化顺, 闵光辉. AZ451镁合金薄带的组织和力学性能研究[J]. 金属学报, 2008, 44(4): 397-402.CHEN Hong-mei, KANG Suk-bong, YU Hua-shun, MIN Guang-hui. Study on microstructures and mechanical properties of AZ451 magnesium alloy sheets[J]. Acta Metallurgica Sinica,2008, 44(4): 397-402.

[10] 王智祥, 刘雪峰, 谢建新. AZ91镁合金高温变形本构关系[J].金属学报, 2008, 44(11): 1378-1383.WANG Zhi-xiang, LIU Xue-feng, XIE Jian-xin. Constitutive relationship of hot deformation of AZ91 magneium alloy[J].Acta Metallurgica Sinica, 2008, 44(11): 1378-1383.

[11] ROBINSON S L, SHERBY O D, SALAMA A. Mechanical behavior of polycrystalline tungsten at elevated temperature[J].Acta Metallurgica, 1969, 17(2): 109-125.

[12] SOMEKAWA H, HIRAI K, WATANABE H, TAKIGAWA Y,HIGASHI K. Dislocation creep behavior in Mg-Al-Zn alloys[J].Materials Science and Engineering A, 2005, 407(1/2): 53-61.

[13] VAGARALI S S, LANGDON T G. Deformation mechanisms in hcp metals at elevated temperatures-Ⅰ. Creep behavior of magnesium[J]. Acta Metallurgica, 1981, 29(12): 1969-1982.

[14] SHI L, NORTHWOOD D O. Strain-hardening and recovery during the creep of pure polycrystalline magnesium[J]. Acta Metallurgica et Materialia, 1994, 42(3): 871-877.

[15] FROST H J, ASHBY M F. Deformation mechanism map[M].Oxford: Pergamon Press, 1982: 44.

[16] MCNELLEY T R, MICHEL D J, SALAMA A. The Mg-concentration dependence of the strength of Al-Mg alloys during glide-controlled deformation[J]. Scripta Metallurgica,1989, 23(10): 1657-1662.

[17] FUNAMIZU Y, WATANABE K. Interdiffusion in the Al-Mg system[J]. Transactions of the Japan Institute of Metals, 1972,13(4): 278-283.

[18] CHEN Hui-qin, CAO Chun-xiao, GUO Ling, HAI Lin. Hot deformation mechanism and microstructure evolution of TC11 titanium alloy in-field[J]. Transactions of Nonferrous Metals Society of China, 2008, 18(5): 1021-1027.

[19] VAGARALI S S, LANGDON T G. Deformation mechanisms in h.c.p. metals at elevated temperatures-II. Creep behavior of a Mg-0.8%Al solid solution alloy[J]. Acta Metallurgica, 1982,30(6): 1157-1170.