基于西门子Simatic Manager平台的冷轧板形控制神经网络效率自学习的实现及效果

包头钢铁集团薄板坯连铸连轧厂自动化部 周 鑫

西门子Simatic Manager软件是西门子公司开发的自动化控制软件。使用STEP7组态工具进行图形化组态：连续功能图(CFC)和顺序功能图(SFC)。控制器硬件平台使用西门子装有64位CPU的TDC控制器，TDC(Techonlogy and Drive Control)是工艺和驱动自动化系统的简称。该系统具有模块化的系统结构，硬件可扩展。采样时间间隔短，可达100sμ，特别适用动态控制任务。中央处理器采用64位结构，可同步多处理器运行，而且具有分时多任务功能，可将运行任务分派到不同的时间片内运行。由于平直度控制涉及大量高实时性的运算，所以单独使用一个双64位CPU的处理单元。

CFC编程工具是标准的图形编程环境，具有强大的功能和使用便捷性，在设计时遵循模块化设计的理念，有非常丰富的功能模块，如位控逻辑、数学运算、通讯功能、输入输出通道、内存管理、特殊的数据处理、物料追踪处理、控制传动模块等。但对于平直度控制，由于其标准库并没有相应的功能模块，所以必须先开发。然后将控制功能封装成标准模块，在CFC编程环境中调用。在Simatic Manager平台上，将NNI神经网络初始化、NNI自学习效率、从NNI中获取效率以及计算执行机构设定值等功能实现后，封装到功能库fbaflc中，在西门子Simatic Manager开发平台的CFC软件设计工具中调用，以完成控制功能。

1.平直度神经网络控制结构

图1-1所示为平直度神经网络控制详细结构框图。NNI为系统辨识器，用于识别执行机构改善的平直度偏差；Y为平直度检测值，Ysr为平直度设定值；Y及Ysr均为包含80个元素的向量。Δσ为当前的平直度偏差；Δiσ为前次激活控制时的平直度偏差；Nσ为NNI辩识的该执行机构能够改善的平直度偏差；P-P为先验的执行机构效率，是80个元素的向量；F为当前的轧制力；W当前轧制板带的宽度；LP为执行机构的实际位置变化；g和P分别为平直度偏差加权因子和执行机构在板带宽度方向上的效率，均为包含80个元素的向量。NCC为用数学方法构成的控制器，向执行机构发出最优设定值。E1为实际改善的平直度偏差，E为网络辨识值输出与实际期望值之间的偏差，用于训练网络。

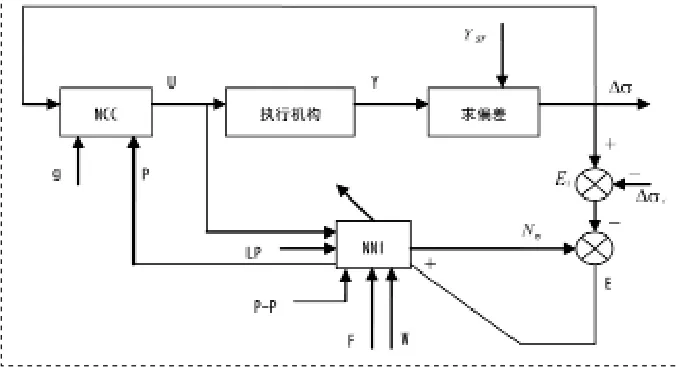
图1 -1 平直度神经网络控制详细结构框图

1.1 执行机构效率

因为平直度测量和第五架轧机之间存在着空间距离，所以必须预先计算出执行机构改善板形的能力。执行机构效率是指执行机构改善板形的能力，其数学公式为其中Niσ，为神经网络NNI计算的执行机构能够改善的板带宽度方向上第i位置的平直度偏差，U为在改善了Niσ偏差时的执行机构输出值。因为在板带宽度方向上共划分了80个区域，所以执行机构效率是一个包含80个元素的向量。pi并不是网络的直接输出，是在网络输出的基础上计算出来的。执行机构效率送入NCC用于计算执行机构的最优设定值。[2]

1.2 NNI效率自学习算法

执行机构效率辩识器NNI采用的是BP算法下面介绍NNI的特征函数和改进的权值调节方法。

(1)特征函数。特征函数取S型函数，即：

F(x)=1/(1+e-x)

(2)改进的权值调节算法

网络采用的BP算法是前向计算输出和反向误差传播的权值调节过程。设网络中第I层某个神经元i与后一层第J层的连接权值为wij，对节点i来说，设输入为xi，输出为xi，xj为后一层中节点j对第I层神经元1的输入。由图1-1可得：

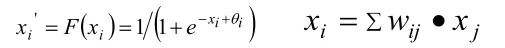
误差反传用改进的Delta权值调整公式：

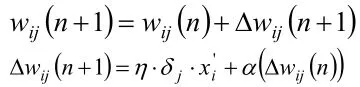
式中：η为学习率(取η=0.1-0.9)；α为动量系数(取α=0.1-0.8)；jδ为神经元输出误差。[3]

2.执行机构效率自学习NNI的实现

2.1 执行机构自学习效率的获取

执行机构效率在神经网络的自学习作用下，逐步得到改善。但是，在CFC软件内怎样取得效率呢?FBAFLC模块库提供了几个此类模块，用来完成这类任务。这个过程分为两步，第一步，从NWA和NWE指向的数据区取得所有执行机构的效率，第二步，根据执行机构数目和每个执行机构效率的离散点数目取得每个执行机构的效率。上述第一步如图2-1所示。上述第二步如图2-2所示。

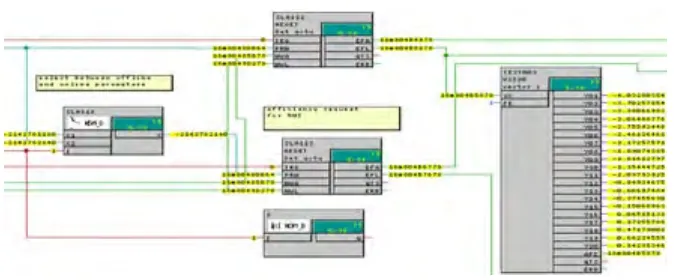
图2 -1 根据类型取得所有执行机构效率

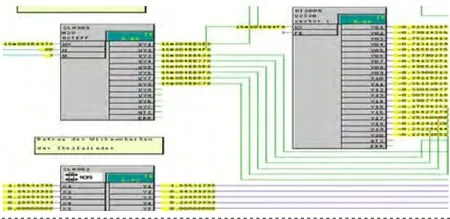
图2 -2 取得某个执行机构效率

在图2-1中，通过功能块AEGET获得所有执行机构的效率，当输入端TRG激活为1时，触发此功能块。输入PRM是一个向量指针，该向量有两个元素：当前获取效率板带的宽度和轧制力类型。NWA和NWL是指向所有执行机构效率的指针。EFA输出为指向所有执行机构先验效率的指针，EFL输出为指向所有执行机构自学习效率的指针。V2S20模块输出首地址为VX输入，而偏移值从FE开始的20个向量元素值。其中离线和在线参数是指：当前正在轧制的板带类型参数是手工通过HMI输入的还是接收二级系统设定的。

功能块M2V从输入端MX指向的向量空间取得各个不同执行机构的效率向量，此效率向量的元素数目为80，并将向量地址输出到VY2-VY8上。它的输入MX是图2-1中的AEGET的输出EFA或EFL，根据从HMI上选择是使用先验效率还是学习效率，将AEGET的输出EFA或EFL连接到此处。图中NOP8块将输入发送到输出。

2.2 执行机构效率自学习的实现

执行机构效率自学习的实现也是通过在CFC软件设计工具中调用封装的学习算法模块实现的。如图2-3所示。

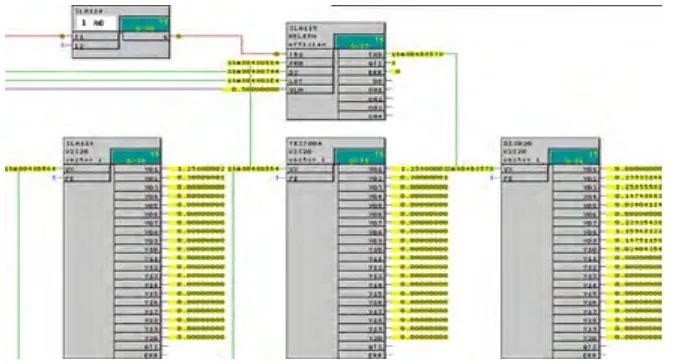
图2 -3 执行机构效率的自学习

在图2-3中，AELERN模块实现了平直度执行机构效率的自学习，它内部封装了BP网络的学习过程。当触发端TRG的输入为1时，激活自学习功能。PRM为包含两个元素向量，表明当前学习执行机构效率时的板带宽度和轧制力。DS为指向执行机构位置变化向量的指针，LDT为指向平直度变化向量的指针。VLN为执行机构效率自学习速度，在此处经过调试设定为0.5。而自学习使用的执行机构最优值通过内部数据结构获得。TDH是一个向量指针，通过它可以在程序内部查看学习效率，如图2-3中的DIS020模块。但更重要的是，它是一个内部使用的全局数据指针，指向执行机构效率学习初始化模块AECONF的MWA和MWL数据区。所以在开发CFC软件时，必须注意AECONF和AELERN之间的一一对应的关系和他们的唯一性。通过平直度的变化和执行机构的位置，AELERN模块自学习对应板带宽度和轧制力类的执行机构效率，并把他们写入TDH指向全局数据区的对应位置。

3.平直度控制效果及总结

图3-1所示的两幅图为经过神经网络自学习进行辨识，控制执行机构，不断改善的板形质量对比，颜色越深为板形质量越不好的区域。可见板形质量得到了明显改善，但从第二幅图目前的板形质量图可以看出带钢边部板形仍存在较大缺陷，所以板形的神经网络控制仍有提高精度的潜力。

图3 -1 带钢板形质量改善情况对比

带钢平直度偏差经过计算分析，可以表现为以下几种(这几种因素可能同时存在)。

(1)偏差值呈由大到小(或由小到大)顺序的线性分布；(2)偏差值呈两边对称的二次曲线分布；(3)偏差值呈对称的四次曲线分布；(4)非对称的局部偏差值。

支撑辊压下倾斜仅影响平直度偏差的线性部分。中间辊的轴向窜动影响平直度偏差的二次曲线部分。而弯辊系统主要影响平直度偏差的四次曲线部分，这主要是因为弯辊调节时，对带钢的边缘影响要比中间大的多。工作辊多区冷却影响不对称的局部的平直度偏差，但多区冷却由于热传导的滞后性，所以控制结果在秒级才能生效，因而在设计它的控制器时将采用PI调节器。

采用神经网络控制方法对冷轧板形进行控制，较好的实现了控制精度和效果。

[1]Flantness Control FLC System Reference Manual for Cont.Pickling Line＆Tandem Mill[Z].Section 5.3.3.10.2004:1-128.

[2]周鑫.五机架CVC冷轧机板形检测与神经网络控制[D].内蒙古工业大学工程硕士学位论文,2008.

[3]徐丽娜.神经网络控制[M].北京:电子工业出版社,2003:55-72.