基于中位参数等价权回归法的谐波阻抗分析

苏攀,郭成,易东

(1.西南交通大学电气工程学院,成都 610031; 2.云南电网公司电力研究院,昆明 650217)

基于中位参数等价权回归法的谐波阻抗分析

苏攀1,郭成2,易东1

(1.西南交通大学电气工程学院,成都 610031; 2.云南电网公司电力研究院,昆明 650217)

为了更好的克服回归法估计谐波阻抗时样本中异常数据的干扰,提出了一种改进算法。通过同步测量公共连接点的谐波电压和电流,将其按照实部虚部进行分解,可以得到以系统谐波阻抗以及谐波电压为回归系数的回归方程。利用中位参数法得到系统谐波阻抗的初步估计,再根据等价权迭代计算谐波阻抗最终估计,进而得到用户谐波发射水平估计。该方法改进了普通稳健回归法以最小二乘解为迭代初值的缺点,具有更好的抗差性,对谐波阻抗的估计更加准确。通过实验分析验证了该方法的准确性。

谐波发射水平;谐波阻抗;中位参数;等价权回归法;稳健性

1 前言

电网中的谐波含量不断增大,谐波污染日益严重,对整个电力系统包括电网中的发供电设备和用户的用电设备均会产生不良的影响[1]。为了解决谐波问题,合理评估用户谐波发射水平和对即将投入的容量较大用户进行谐波源评估显得尤为重要[2]。目前国内外对于谐波发射水平的评估方法还是主要围绕对系统和用户谐波阻抗的估算来展开[3]。

现有的谐波阻抗测量方法可以分为注入式和非注入式两种。注入式方法需要强功率的信号发生器,并且很有可能影响系统的正常运行。非注入式方法主要包括波动量法[3-4]、开关元件法[5],回归法[6-9]等。回归法由于对系统的正常安全运行完全没有干扰,得到了广泛的关注和研究。二元线性回归法[7]采用最小二乘法受异常值的干扰较大;基于等价权的回归法[8]虽然在一定程度上能够减少异常数据的干扰,但是其以最小二乘估计为初值会降低抗差估计性能;中位数回归法[9]有较强的抗差能力,但由于未考虑异常数据的权重仍然会有较大误差。

针对上述情况,综合考虑中位参数法与等价权回归法各自的优点,提出基于中位参数初值的等价权稳健回归法[10]进行谐波阻抗以及用户谐波发射水平的评估。首先选择不同的样本组合计算得到估计值并得到参数的中位数,从中选择最接近中位数的一组估计值作为迭代初值,之后进行等价权回归估计得到最终结果。

2 中位参数等价权回归法基本原理

在谐波阻抗评估分析中,经过实部虚部分解,回归方程一般为二元回归方程。其最基本的回归方程为：

y=b0+b1x1+b2x2(1)

其中样本为 (y,x1,x2),回归系数为 (b0, b1,b2)。假设一共有m组样本观测值,即有m个观测方程,从中选择n个方程估计回归系数,则可以得到p=Cnm组回归系数解。提取每组解向量中的第i(i=0,1,2)个元素,构成新的p维向量bi= [b1i,b2i, b3i…,bpi],求取向量bi中位数,将其median(bi)设为,则三组p维向量b0, b1,b2的中位数构成中位参数向量为

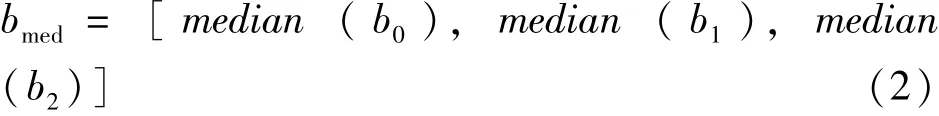
计算p组解向量与中位参数向量的差值Δbk= bk-bmed,(k=1,2… p),对于p组差值向量,求各组差值向量的二范数,有

则最小值min(Δb)所对应的解向量即为所求的中位参数解。根据中位参数解 (^b0,^b1,^b2)利用δai=yi-^b0-^b1x1-^b2x2可得到m组样本观测值的残差向量δa=(δa1,δa2,…δam)取单位权中误差δ= 1.438median(|δa1|,|δa2|,…|δam|)。

将中位参数法得到的解向量作为回归估计的初值解,再根据等价权法进行迭代回归计算。在本文中选取应用最广泛的IGGⅢ方案[11],其相关等价权函数为：

式中,k0=1.0～1.5,k1=2.5～3.0。

基于中位参数等价权回归法的具体计算步骤如下：

1)根据中位参数法得到初始估计值^b0;进而可得初始残差δa0;

2)根据δa0计算啄0;

3)利用IGGⅢ方案计算得到等价权函数P1,得到初始权重,回归计算得到估计值^b1;

4)将步骤 (3)中的估计值代替步骤 (1)的估计值,得到新的残差以及单位权中误差;

5)返回步骤 (3)中,计算得到新的估计值,以此类推进行迭代回归计算。如果新的估计值与前一个估计值的绝对值之差最大值小于给定的某一个误差参考值,则迭代结束。

3 基于中位参数等价权回归法谐波阻抗评估

采用回归法对系统谐波阻抗进行评估,通常电路等效为系统侧和用户侧两部分,其等效电路如图1所示。

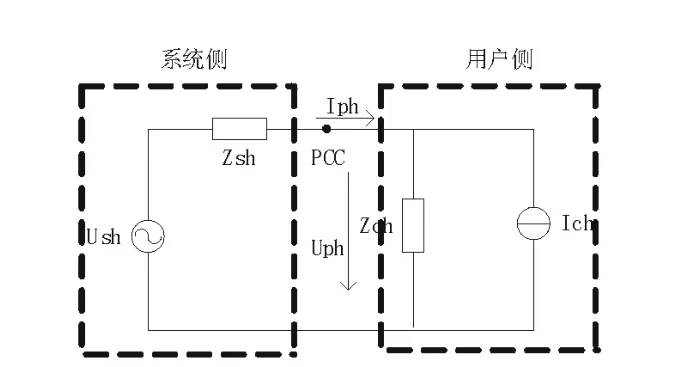
图1 计算谐波阻抗等值电路

图1中,U·sh为系统侧h次谐波等效电压源,·Ich为用户侧h次谐波等效电流源,Zsh和Zch分别

··为系统侧和用户侧等值谐波阻抗。Uph和 Iph分别为公共连接点的h次谐波电压和电流。根据等值电路可以得到方程：

···

Uph=Ush-ZshIph(5)

按照实部虚部展开,以x表示实部,y表示虚部,可得：

式中,Uphx,Uphy分别为PCC处h次谐波电压的实部和虚部;Iphx,Iphy分别为PCC处h次谐波电流的实部和虚部;Ushx,Ushy分别为系统h次谐波等效电压源的实部和虚部;Zshx,Zshy分别为系统h次谐波阻抗的实部和虚部。

在通常情况下,用户侧谐波阻抗远远大于系统侧谐波阻抗,因此根据得到的系统谐波电压源可以近似求得用户谐波发射水平：

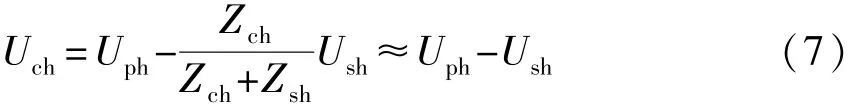
4 实验数据分析

根据图1等效电路搭建仿真模型进行计算,

·系统侧3次谐波等效电压源Ush为200∠45°V,用户侧3次谐波等效电流源·I均值为10+j17 A,系

ch统侧等值谐波阻抗Zsh均值为5+j23 Ω,用户侧等值谐波阻抗Zch均值为50+j310 Ω。

采样1 440个PCC的电压电流数据模拟实测数据,为了验证算法的性能,令PCC谐波电压的采样数据在 (10,100,300,400,600,700, 800,1 000,1 200)点产生异常值,如图2所示。在进行回归计算时取60组数据作为样本空间即样本分别为1～60,2～61,3～62,……,1 381～1 440,可得1 381个回归系数解,分别利用二元回归法,普通等价权法,中位参数等价权法进行计算,得三组不同结果。如图3所示。

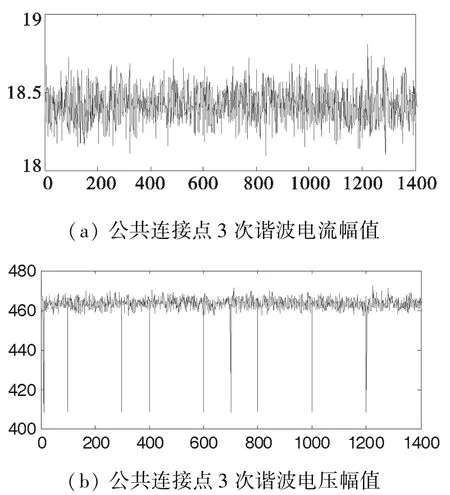
图2 公共连接点3次谐波电压电流幅值

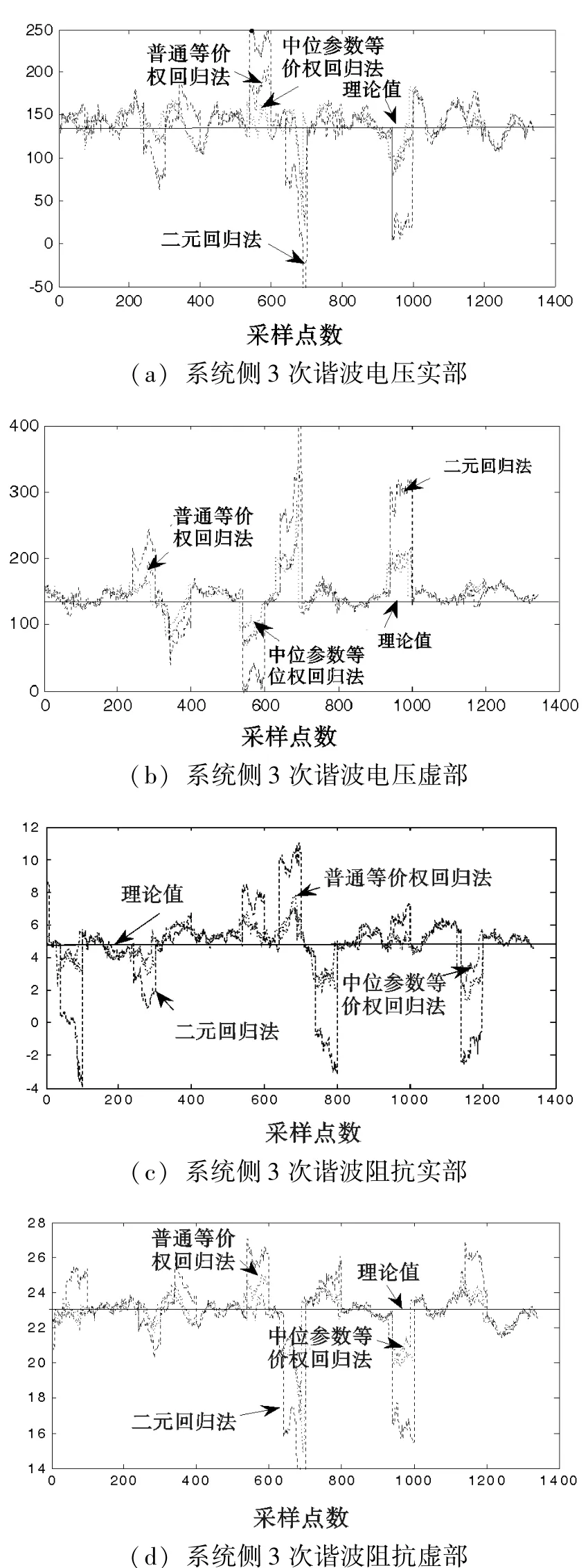
图3 三种方法分析计算系统谐波电压与谐波阻抗结果

根据图3的仿真结果可以看出,在正常点时,二元线性回归法,普通等价权法以及中位参数等价权法计算结果均接近理论值。但在异常值(10,100,300,400,600,700,800,1 000,1 200)点,可以看到二元线性回归法稳健性最差,因为其并未考虑异常数据的干扰;基于中位参数的等价权法稳健性要好于普通等价权法,其结果更接近理论值。将图3中系统谐波电压与谐波阻抗估计值求平均,可以得到三种方法估计均值与理论值的误差,如表1所示。

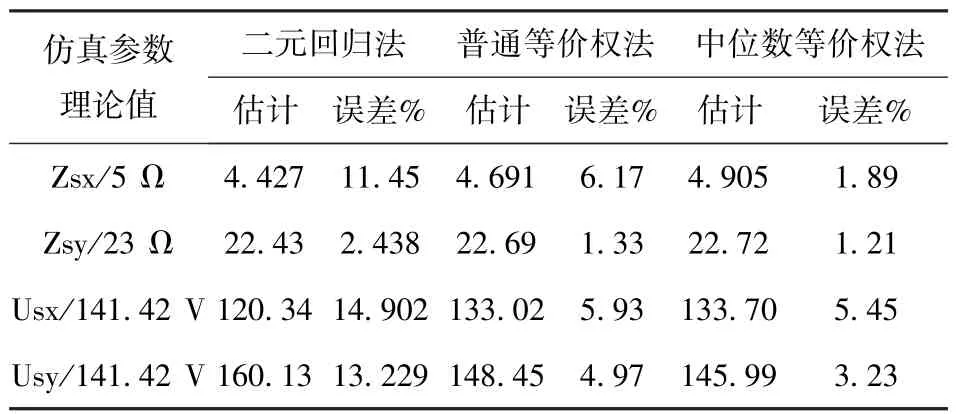
表1 系统谐波电压源与谐波阻抗估计平均值

从表1及图3结果可得出,基于中位参数的等价权回归法所得结果最接近理论值,估计精度最高。

根据式 (7)计算用户谐波发射水平为

Uch≈Uph-Ush=265.5(V) (8)

用户谐波电压占公共连接点总的谐波电压的57.28%,与理论计算结果基本吻合。

5 结束语

文中提出运用中位参数等价权回归进行系统谐波电压源和系统侧谐波阻抗估计的方法,通过理论仿真分析证明以下结论：

1)该方法改进了普通稳健回归法以最小二乘解为迭代初值缺点,具有更强的抗差性,计算结果更接近于真值。

2)该方法迭代初值已经具有抗差性,因此相对于普通稳健回归法所需计算时间较短,实时性更好,适用于在线谐波阻抗测量。

3)由于抗差性更好,该方法适合对波动性较大的系统如牵引供电系统等进行分析。

[1] 王晓亮,李娜.基于加窗插值FFT算法的间谐波检测方法研究 [J].现代电力,2012,29(5)：28-31.

[2] 祝石厚,侯世英,吕厚余.电力系统谐波分析的有效方法-谐波状态估计技术综述 [J].现代电力,2007,24(3)：6-10.

[3] 龚华麟,肖先勇,刘亚梅,等.基于主导波动量筛选原理的用户谐波发射水平估计方法 [J].中国电机工程学报, 2012,30(4)：22-27.

[4] Jin Hui,Honggeng Yang,Shunfu Lin,Maoqing Ye.Assessing Utility Harmonic Impedance Based on the Covariance Characteristic of Random Vectors[J].IEEE Transactions on Power Delivery,2010,25(3)：1778-1785.

[5] 吕洋,徐政.投切电容器时的电网谐波阻抗测量方法 [J] .高电压技术,2009,35(7)：1780-1784.

[6] XU W,LIU Yilu.A method for determining customer and utility harmonic contribution at the point of common coupling[J]. IEEE Transactions on Power Delivery,2000,15(2)：3-16.

[7] 张巍,杨洪耕.基于二元线性回归的谐波发射水平估计方法 [J].中国电机工程学报,2004,24(6)：50-54.

[8] 车权,杨洪耕.基于稳健回归的谐波发射水平估计方法[J].中国电机工程学报,2004,24(4)：39-44.

[9] Rousseeuw P,WagnerJ.Robust Regression with a Distribution Intercept Using Least Median of Squares[J].Computational Statistics&Data Analysis.1994,17：65-76.

[10] 杨玲,沈云中,楼立志.基于中位参数初值的等价权抗差估计方法 [J].测绘学报,2011,40(1)：28-31.

[11] 刘经南,姚宜斌,施闯.基于等价方差-协方差阵的稳健最小二乘估计理论研究 [J].测绘科学,2000,25(3)：2-5.

Harmonic Impedance Analysis Based on Median Parameter Equivalent Weight Regression Method

SU Pan1,GUO Cheng2,YI Dong1

(1.School of Electrical Engineering,Southwest Jiaotong University,Chengdu 610031; 2.Yunnan Electrical Power Experiment Institute,Kunming 650217)

In order to overcome the interference of abnormal data in samples when use regression method to estimate harmonic impedance,a new method was proposed.By simultaneous measurement of the harmonic voltage and harmonic current of PCC,decomposition in accordance with the real part and the imaginary part,regression equation which system harmonic impedance and harmonic voltage as regression coefficient could be get.Median parameter method was used to get the system harmonic impedance preliminary estimate and equivalent weight regression was used to compute the final results,consequently the harmonic emission level of customer could be calculated.This method is the combination of the respective merits of median parameter method and weighted regression method,which has better robust ability and is more accurate estimates of harmonic impedance.The validity of the method is verified by simulation analysis.

harmonic emission level;harmonic impedance;median parameter;equivalent weight regression method;robust abilit

TM81

B

1006-7345(2014)01-0005-04

2013-09-10

苏攀 (1989),男,硕士研究生,西南交通大学,主要研究方向为电能质量分析与控制 (e-mail)supan07@163.com。

郭成 (1978),男,博士,云南电网公司电力研究院,主要研究方向为电力系统分析、电能质量控制。

易东 (1971),男,讲师,西南交通大学,主要研究方向为电气化铁道电能质量分析与控制,电力系统继电保护。