基于预防性成组维修的人字门船闸大修周期

陈一梅 李少斌 金彬彬

(东南大学交通学院，南京210096)

船闸大修涉及专业多、工期长、耗用资金大，大修周期的合理性直接影响船闸维护费用和交通效益.文献[1]对船闸底枢的可靠性进行分析，计算了底枢平均故障间隔时间.文献[2]从一个大修期内年均费用最低的角度建立船闸经济寿命模型，但忽略了船闸的系统性和维修策略对大修的影响.

在设备维修研究中，国内外许多学者[3-5]从故障相关性、结构相关性和功能相关性等方面研究多部件系统成组维修优化问题，并建立了以最小系统维修成本为目标的数学模型.本文基于设备成组维修理论，建立人字门船闸大修周期优化模型，研究人字门船闸在成组维修策略下的最优大修周期.

1 船闸的成组维修

1.1 成组维修优化策略

成组维修分为修复性成组维修、预防性成组维修和机会成组维修3类[6].船闸维修需在满足工时、人力、备件等维修资源条件下进行，国内外船闸维修以预防性维修为主，即以可靠性和经济性为目标，预先制定维修计划，以确保维修工作顺利完成.

预防性成组维修分为直接成组和间接成组[7].本文采用直接维修成组与间接成组相结合的方式，将所有部件按照其维修间隔期分成不同的组，每组都有各自的维修间隔期，当某个时刻存在多组维修任务时，可将多组维修任务结合在一起进行.系统维修最为经济时，将全部维修任务同步进行，即进行大修.如图1 所示，t1，t2，t3，t4为各组的维修间隔期，t3=2t1，在 2t1，4t1，6t1，8t1时间点时可同时进行部件第1组和第3组的维修，在6t1时刻可同步进行部件第2组的维修，在10t1时维修效益到达最优，对系统进行大修.

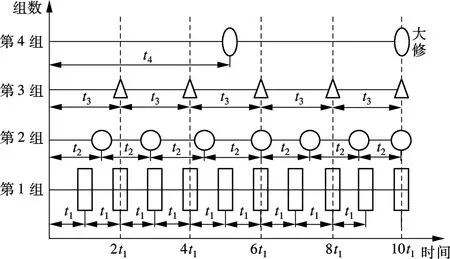
图1 船闸成组维修示意图

1.2 船闸成组维修部件构成分析

船闸系统由土建、机械和电气3部分组成.土建部分设计寿命长，破损没有明显的周期性，一般在大修工程中视情维修，可不列入多部件成组维修系统.电气部分的故障可在日常维修中安排，也不列入成组维修系统.机械部分的部件工作环境复杂、工作强度大、易腐蚀、易磨损，寿命相对较短，维修难度大，是否正常工作对船闸运行有重要影响，因此将机械部分作为船闸系统成组维修的主要控制子系统.

船闸机械部分包括底枢、顶枢、阀门、支承件、闸门门体和启闭机.根据故障调查，在现有维修技术下启闭机故障排除不需停航，纳入常态维修.闸门门体在现有材料和加工技术下，其使用寿命远大于其余部件，做好相关运转件的维修工作可保证门体的正常工作，因此启闭机和门体不列入成组维修的部件.底枢、顶枢、阀门、支承件相关性较强，底枢发生较严重磨损不及时维修，会导致承压条偏磨，从而引起系列故障(如承压条破损、旋转轴线及支承轴线的偏移、顶枢拉杆超载等).顶枢、支承件失效对其余部件也产生相应的影响，因此本文选取底枢、顶枢、阀门和支承件作为船闸大修周期研究的4个控制部件组，并对其进行成组维修优化.

1.3 船闸成组维修费用分析及计算

船闸成组维修费用CW由直接维修费用CZ和维修停航所导致的过闸损失费CS构成，表达式为

1)直接维修费用 考虑时间对现金流的影响，将直接维修费用折算到基准年，则 CZ的表达式为

式中，q为年利率;tj为第j组预防性维修间隔期;M为船闸系统维修可分成的总组数;N为第j组预防性维修的维修次数，N=INT(T/tj)，INT(T/tj)为取整函数，T为大修周期;N(j，tj)为预防性维修状态函数，表示T内第j组部件是否经过维修，可用下式表示:

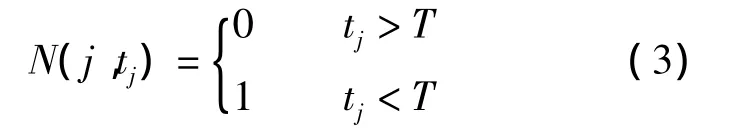
式中，tj＞T，表示未进行预防性维修，记为0;tj＜T，则部件在tj时进行预防性维修，记为1.Cpj为第j组的预防性维修费用，此费用受市场因素的影响逐年变化.

2)过闸损失费用 CS的表达式为

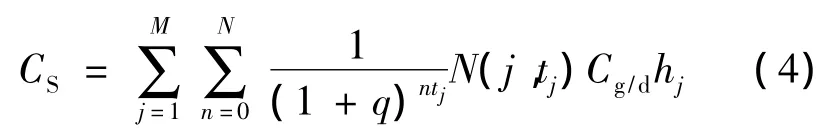
式中，Cg/d为停航每天损失的过闸费用;hj为第j组预防性维修所需天数.

将式(2)～(4)代入式(1)，可得CW的表达式为

2 基于预防性成组维修的船闸大修周期模型

2.1 模型基本假设

1)维修资源足以满足所有维修任务的要求，不需要在优化时考虑资源的限制.

2)船闸部件在大修后为全新状态.

3)假设船闸每天运行的闸次基本相同.

4)船闸部件属于专用部件，更换过的旧部件的残值为零.

2.2 船闸大修周期模型建立

一个大修期的船闸系统总费用分为初始投资CC、成组维修费用Cw和折算到初始年的年养护费用总和CY;船闸大修后状态恢复如初，因此CC为上次大修总费用.年养护费用的总和为

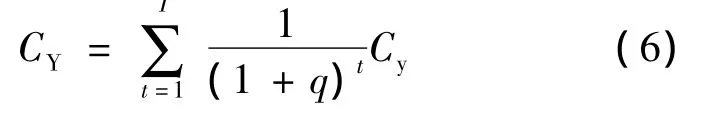
式中，Cy为年养护费用，因部件的劣化和市场因素呈逐年增强.

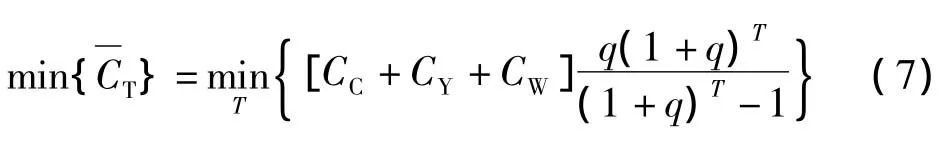
3 实例计算

以苏北处的人字门船闸为例，计算人字门船闸最优大修周期.

3.1 维修间隔期的确定

为了使控制部件的维修间隔期具有可比性，同时又符合船闸管理维护习惯，引入标准年概念.根据京杭运河苏北段人字门船闸通过水平，取每日运行45闸次，年通航天数320 d，则根据闸次折算后的标准年A为

式中，A为标准年;n为运行闸次.

对京杭运河苏北段所辖16个人字门船闸控制部件的寿命周期进行调查统计，各控制部件更换时运行闸次调查统计结果见表1.

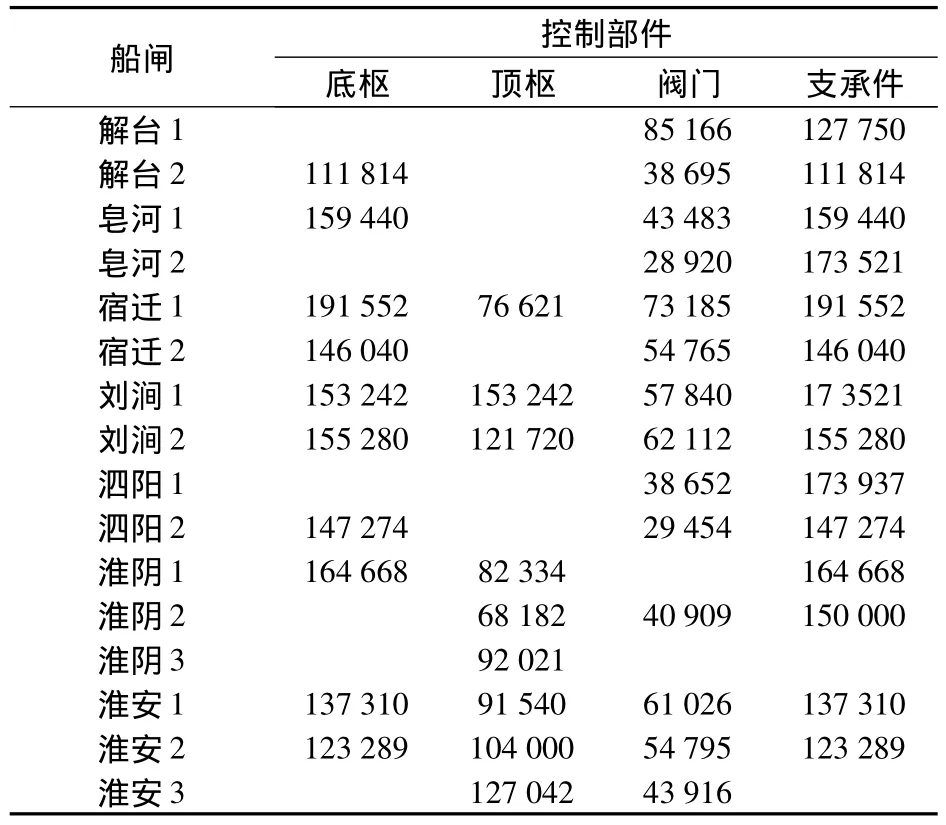
表1 京杭运河苏北段人字门船闸控制部件更换数据表

调查统计发现，京杭运河苏北段人字门船闸系统大修时存在未故障的部件也同时更换的情况，因此若对表1的数据笼统地以完全寿命数据处理，则会造成参数估计的不准确.本文结合人字门船闸的大修检测报告与运转件实验报告，将控制部件的可靠性数据分为2种类型进行处理:① 底枢的摩擦副和支承件更换时磨损轻微，未达到故障状态，作为无故障数据处理，采用多层贝叶斯法估计故障率[8];②顶枢的轴、轴衬和阀门的主滚轮系为视情维修，调查的可靠性数据可作为完全寿命数据分析，采用平均秩次法估计故障率.依据表1对各部件寿命分布选型并进行参数估计(见表2).

表2 各控制部件可靠度函数和分布概率密度函数

顶枢和阀门的维修方式为更换，属于不可修复部件，平均寿命采用失效前平均时间，即

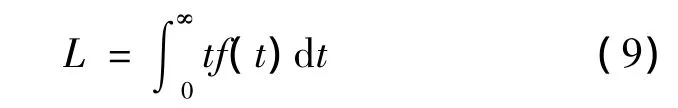
将表2中顶枢和阀门的f(t)分别代入式(9)，计算得到顶枢的平均寿命L=8.6×104闸次，阀门的平均寿命L=5.0×104闸次，维修间隔期(按标准年计)分别为6和3年.

底枢和支承件的寿命采用可靠性模型[9]，按效益费用比最大原则确定可靠度为0.8.依据表2底枢和支承件在达到可靠度标准时，其维修间隔期分别为19.6×104闸次和20.5×104闸次，维修间隔期(按标准年计)为14年.

3.2 经济参数确定

经济参数 CC，Cy，Cpj，Cg/d通过现有船闸维修、抢修和运营记录等资料进行统计确定.

①根据苏北处船闸2011—2012年的4个船闸大修统计资料，大修工程费用CC取700万元.2012年16个船闸Cy平均值为25万，假定由于部件老化与市场价格变动等因素，年养护费用以10%逐年递增.

②Cpj根据2012年刘老涧二号大修工程和专项工程维修费确定初年值，以后每年按照生产价格指数PPI=5%递增;hj根据2002—2011年专项工程时间和刘老涧二线2012年大修工程施工进度表确定;各维修组的Cpj和hj如表3所示.

③船闸施工一般安排在货运通过较少的2月份进行，Cg/d根据2月份船闸每天的过闸费确定，统计可得2011年2月份京杭运河苏北处单个船闸每天通过量为12×104t左右，因此停航期间Cg/d为7.2万元(12万元×0.6，过闸费用征收规定每次每吨征收0.6元).

④年利率取8%进行现值折算，大修时部件的残值取0.

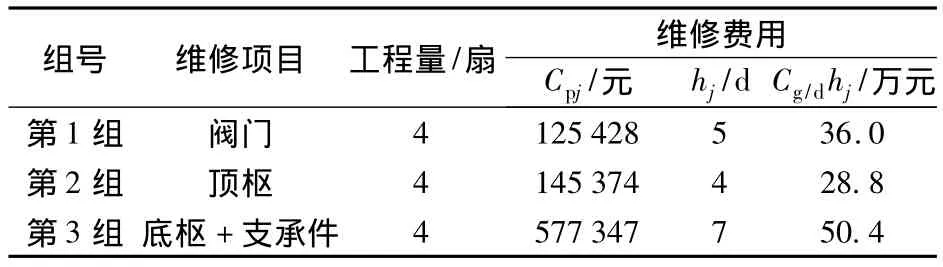
表3 各维修组的Cpj和hj值

3.3 计算结果

3.3.1 大修周期

将3.2节中的成组维修间隔期与各经济参数代入模型，可得表4和图2.由图2和表4可看出，当T=14时最小;当T＞14时随着T增加而增加.图2曲线中的凸点是某时间节点进行成组维修费用突增造成的，凸点与各组维修间隔期同步.由此可确定船闸大修周期为14年.

表4 模型计算过程表

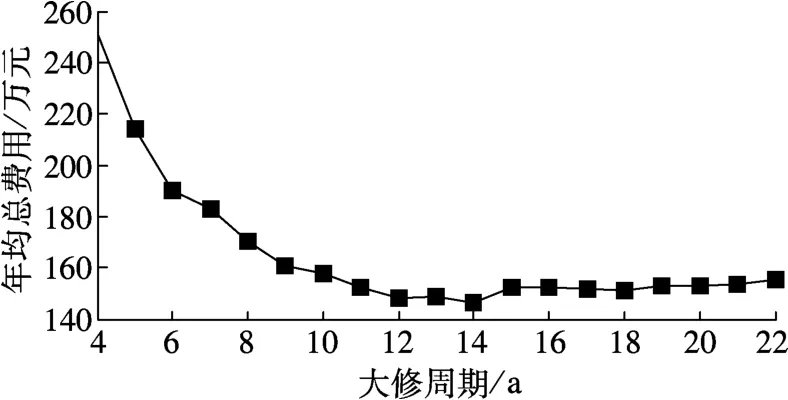
图2 年均总费用与大修周期T关系图

3.3.2 敏感性分析

CC和Cy的确定受市场经济价格变动和人为主观因素等影响，存在不准确性，因此采用敏感性分析方法[10]分析CC和Cy对T的影响程度.

评价指标T对于费用的敏感度系数D为

式中，ΔC为费用的变化率;ΔT为费用发生ΔC变化率时，评价指标T的相应变化率.

根据式(10)可得敏感性分析结果，见表5.

表5 CC和Cy对T的敏感度系数

由表5可见，T对CC和Cy的敏感度系数在0.02～0.12之间，CC和Cy的不确定性对T的影响不大，模型计算结果稳定.

3.3.3 成组维修间隔期对大修周期的影响

目前京杭运河苏北段人字门船闸阀门更换年限为2～6年，顶枢更换年限为5～9年，底枢和支承件平均更换年限为10年.根据实际调查表1和理论计算表3，取第1组阀门的维修间隔期为2～6年，第2组顶枢为5～9年，第3组底枢和支承为10～14年.

令其中一组维修间隔期改变，另2组维修间隔期不变，分析对T的影响，计算结果(见表6)表明:

1)第1、第2组维修间隔期变化对大修周期T的最终结果没有影响.

2)当第3组维修间隔期为10年时，成组维修费用CW较低，初始投资和养护费用所占比例较重，大修周期主要是CC及CY的函数，最佳经济大修周期应为18年，采用10年大修，是不经济的.

3)当第3组维修间隔期为12～14年时，随着第3组维修间隔期的延长，最佳大修周期T也相应延长，并与第3组维修间隔期同步.

表6 各组维修间隔期对T影响表

4 结论

1)人字门船闸是一个综合性较高的系统，其运行环境复杂，组成设备众多，但是，船闸机械部分是影响船闸大修的主要控制子系统，其中底枢、支承件、顶枢和阀门是4个控制部件.基于可靠性理论，底枢和支承件的寿命采用可靠性模型，维修间隔期为14标准年;顶枢和阀门属于不可修复部件，采用失效前平均时间计算模型，维修间隔期分别为6和3标准年.

2)成组维修策略对京杭运河苏北处所辖的人字门船闸大修周期影响明显，随着主要控制部件底枢和支承件的维修间隔期延长，船闸大修期也随着延长.因此，管理者可通过提高底枢和支承件的维修工艺和养护水平延长其维修间隔期，从而延长船闸的大修周期，实现经济最优的目标.

3)按照京杭运河苏北段目前的底枢材料、维修工艺和管理水平，从系统成组维修的可靠性和经济性来看，人字门船闸的最优大修周期为14标准年.

References)

[1] 陈一梅，马丽佳，王建民.船闸底枢可靠性模型及其应用[J].东南大学学报:自然科学版，2011，41(1):205-209.Chen Yimei，Ma Lijia，Wang Jianmin.Reliability model of lock bottom assembly and its application[J].Journal of Southeast University:Natural Science Edition，2011，41(1):205-209.(in Chinese)

[2] 马丽佳，陈一梅.一种基于经济寿命理论的船闸大修周期确定方法[J].水运工程，2010(3):121-125.Ma Lijia，Chen Yimei.Determineation of cycle of lock overhaul based on the theory of economical life[J].Port＆ Waterway Engineering，2010(3):121-125.(in Chinese)

[3] 蔡景，左洪福，刘明，等.复杂系统成组维修策略优化模型研究[J].应用科学学报，2006，24(5):533-537.Cai Jing，Zuo Hongfu，Liu Ming.Optimal group preventive maintenance model for complex systems[J].Journal of Applied Sciences，2006，24(5):533-537.(in Chinese)

[4] Radouane L，Alaa C，Djamil A.Opportunistic policy for optimal preventive maintenance of a multi-component system incontinuous operating units[J].Computers and Chemical Engineering，2009，33(99):1499-1510.

[5] Sheu Sheyhuei，Jhang Jhyping.A generalized group maintenance policy[J].European Journal of Operational Research，1996，96(2):232-247.

[6] 杨元，左黎放，刘振宇，等.基于相关性的系统预防性维修任务成组优化[J].武汉大学学报:工学版，2012，45(4):539-544.Yang Yuan，Zuo Lifang，Liu Zhenyu，et al.Optimal grouping preventive maintenance of a system under dependencies[J].Engineering Journal of Wuhan University:Engineering Edition，2012，45(4):539-544.(in Chinese)

[7] Mobley R K.An introduction to predictive maintenance[M].New York:Elsevier Science，2002:10-12.

[8] Dekker R，Vander D F，Wildeman R.A review of multicomponent maintenance models with economic dependence[J].Mathematical Methods of Operations Research，1996，45(45):411-435.

[9] 王灵芝，徐宇工，张家栋，等.铁路设备关键零部件的可靠性分析模型及其应用研究[J].铁道学报，2008，30(4):93-97.Wang Lingzhi，Xu Yugong，Zhang Jiadong，et al.Research on reliability analysis model for key components and parts of railway equipment and its application[J].Journal of the China Railway Society，2008，30(4):93-97.(in Chinese)

[10] Borgonovo E，Peccati L.Uncertainty and global sensitivity analysis in the evaluation of investment projects[J].Journal of Production Economics，2006，104(1):62-73.