基于双层规划的应急救援车辆调度模型

夏红云 江亿平 赵林度

(东南大学系统工程研究所，南京210096)

近年来，大规模灾难性事件频发，给人类造成了巨大的生命与财产损失.2013年的雅安地震造成196人死亡，11 470人受伤.在地震发生后的短时间内，各灾区医疗资源极度匮乏，全国各地对雅安灾区迅速实施了医疗资源支援.由此发现，大规模灾难性事件会产生对应急医疗资源突发的、迫切的、大量的需求，而现实背景下医疗资源供应点的可用物资量与物资配送车辆受应急准备限制，在灾害发生后的短时间内通常会供不应求，运输车辆也必须承担多次、分阶段的调度任务.因此，如何在特定时间域内，通过多阶段车辆调度将应急医疗资源从多个供应点配送到多个需求点，以最大化灾区需求满足量是应急救援中亟待解决的关键问题.

应急物资车辆调度是传统车辆路径问题(vehicle routing problem)在应急情境下的一种演化.传统车辆路径问题用以解决最小化运输成本目标下将m个供应点的物资运送到n个需求点的车辆路径规划.自1959年Dantzing等[1]提出车辆路径问题以来，该基本问题已有各种各样的变化与拓展.基于车辆路径问题中各参数的特征，可将拓展类型简单归纳为以下几种:多路径(multi-trip)车辆调度、分批到达(split delivery)车辆调度、带取送的(pickup and delivery)车辆调度、多阶段车辆调度(multi-period)等[2-7].上述问题多以最小化总成本为目标，而应急情境下必须以时效性为第一准则，弱化调度过程中的经济性.

关于应急救援车辆调度，Yuan等[8]考虑车辆受灾害影响的速度，构建了应急物流管理路径选择模型.Wohlgemuth等[9]在物资拥有量小于车容量的假设下，建立了灾害救援中的动态车辆调度模型.应急救援车辆调度问题受时间域的限制，会产生多次、多阶段的调度任务.关于多阶段车辆调度，石彪等[10]建立了基于车辆紧缺假设的两阶段应急物资运输车辆调度模型.Wen等[7]针对动态多阶段车辆调度问题，建立了混合整数线性规划模型.文献所提的多阶段车辆调度中，每一阶段车辆的可用数量基本上是已知的，而应急背景下的实时调度中，每阶段可用车辆数量随时间及上一阶段的决策而动态变化.

本文考虑在大规模突发事件爆发后的有限时间域内，针对应急救援车辆不足，需要多次、分阶段将应急医疗资源从多个供应点配送到多个需求点的情形，以最大化需求点收益、最小化延迟成本为目标，采用网络流理论及双层规划建模方法，构建了含时间窗的应急救援车辆多阶段调度模型，并应用基于动态规划的两阶段启发式算法进行求解.算例结果验证了该算法的可行性，上下层相互制约与合作推动了全局最优的实现.

1 问题描述

从网络流的角度来看车辆调度问题，假设整个有向图为G=(I∪J，A)，其中I为供应点的集合，J为需求点的集合，A为弧的集合.假定离散有限决策时间域为集合{0，1，…，T}.时间域T内，每个供应点的医疗物资存储量为固定量si，每个供应点i的车辆拥有量为ki，所有车的车载量均为Q，车辆集合为K.各需求点的需求量为dj，根据灾情给定的收益权重为βj，每个需求点的物资保障最低标准为αj.需求点j的最低标准保障量应在bj时刻到达(设为bj整数时刻)，否则会产生延迟成本.每条弧a(i，j)∈A 的运输时间为 cij，其中 i∈I，i∈J.

本文构建的应急救援车辆调度模型基于如下基本假设:

①每辆车一次只访问一个需求点;

②装卸时间小于车辆运输行驶时间，暂不考虑;

③每辆车完成任务后立即返回原出发点待命;

④时间域T内，除每个需求点最后一次运输或者供应点物资匮乏外，每辆车都必须满载.

2 双层规划模型

本文采用双层规划方法对问题进行建模.上层规划用以决策供应点到需求点的最优配送量，下层规划用以决策在给定最优配送量基础上的各阶段车辆调度方案.上层规划与下层规划的相互制约与合作推动了整体优化的实现.

2.1 上层规划

上层规划的目标函数为

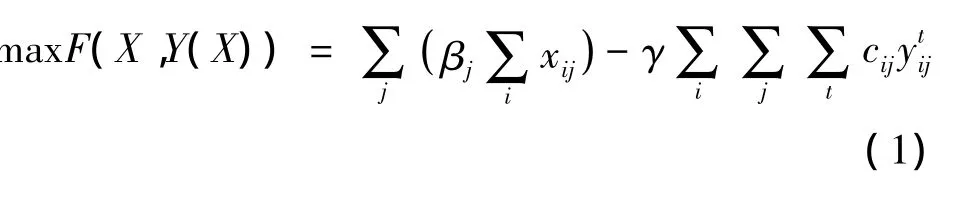
式中，X为上层规划中的上层决策解集;xij为上层决策变量，表示时间域T内需要从供应点i配送到需求点j的医疗资源总量;Y为上层规划中的下层决策解集为下层决策变量，表示t时刻从供应点i调配到需求点j的车流量;γ为权重系数.

约束条件为

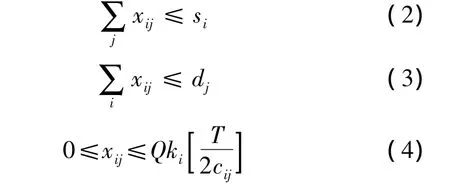
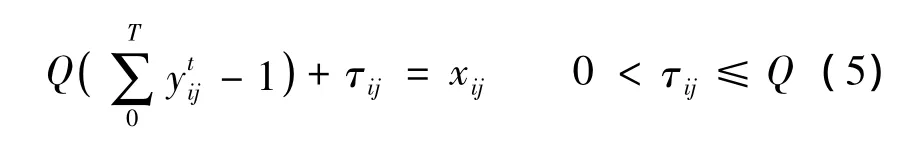
式中，τij为松弛变量，表示供应点i到需求点j最后一次的运输量.

上层规划中以最大化需求点收益、最小化时间域T的总时间成本为目标，满足式(2)和(3)的供应约束条件与需求约束条件，即供应点i配送的医疗资源总量不能超过其可供应量，需求点j所获得的总资源量不能超过其需求量.式(4)表明，供应点i配送到j个需求点的医疗资源量不能超过供应点i所拥有车辆能够配送的数量上限.式(5)反映了与xij的关系，是下层规划对上层规划的反应函数.

2.2 下层规划

下层规划的目标函数为

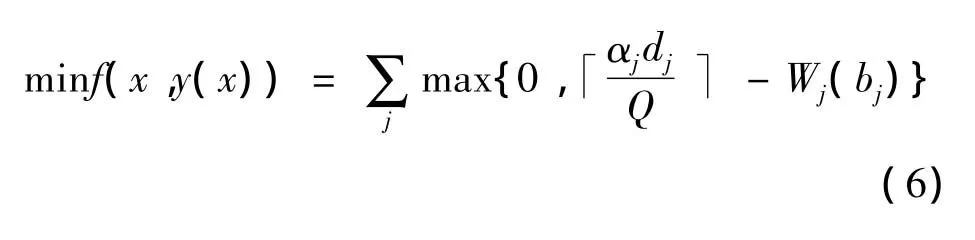
约束条件为

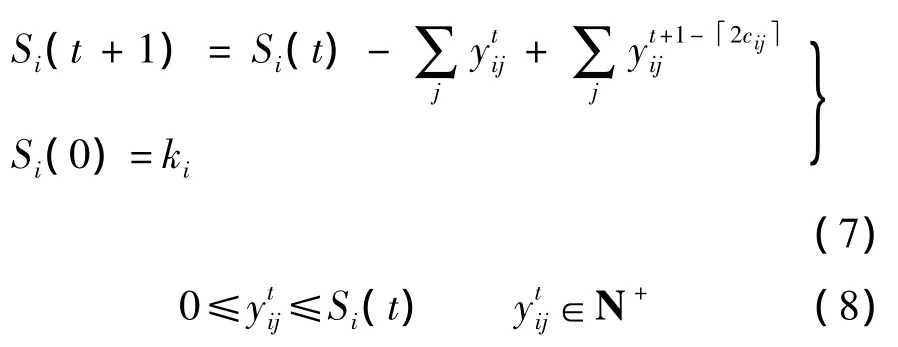
式中，Si(t)为t时刻供应点i拥有的车辆数.

下层规划的目标是在满足上层规划设定的物资量分配的基础上最小化车辆延迟成本.本文的延迟惩罚函数是关于bj时刻需求点j所累积到达的物资量的线性函数.由于t时刻从供应点i调配到需求点j的辆车将在时刻到达需求点j，故可以得到式(6)的关于需求点j车辆的流量守恒公式.

3 算法与算例

3.1 算法

本文双层规划的求解类型是对上下两层反复求线性规划，在上层收敛时得到上层最优解，从而引诱下层最优解.对于上层线性规划，本文利用Matlab软件中线性规划求解函数进行求解;对于下层整数规划，本文采用基于动态规划的两阶段启发式算法求得整数最优解.具体步骤如下.

1)设定初始解X0，令迭代次数r=0.

2)对于给定的Xr，找出由供应点i覆盖的Ni个需求点，将其分为2类:第1类是只由供应点i覆盖需求点j的需求;第2类是除了供应点i还有其他供应点覆盖需求点j的需求.然后，分别按照bj的大小将需求点从小到大进行排序，且第1类中需求点集体优先.因此，下层最优解分2个阶段进行:①将Ni个需求点的车辆调度分为Ni个有序阶段进行，令 ni=1，V(0)=0.如果 t≥bj，则停止迭代;否则，令在时间域T内，以为需求点j每阶段车流量分配的整数基准，在其中a∈N+)的整数范围内设定)'，使得 V(ni)=，令.如果 ni=Ni，则停止迭代;否则，令ni=ni+1，继续迭代.②将Ni个需求点的车辆调度分为Ni个有序阶段进行，令ni=1，V(0)=0，t=bj.如果t=T－1，则停止迭代;否则，令在时间域T内，以每阶段车流量分配为整数基准，在整数范围内设定，令，使得需求点j的总到达物资满足上层分配量.

3)根据式(5)计算τij，将关系式－)/Q+1代入上层目标函数，求解上层问题，得到一组新的Xr+1值.

3.2 算例

为了更好地理解上述模型，本文考虑某地突发大规模灾害性事件，共计8个灾情严重的区域急需医疗资源，而此时只有3个资源供应点存有有限的医疗物资与可调度车辆.通过算例描述并求解在灾害发生后的12个单位时间内的救援车辆调度问题.表1～表3为各资源供应点与需求点的参数现状.

表1 供应点参数

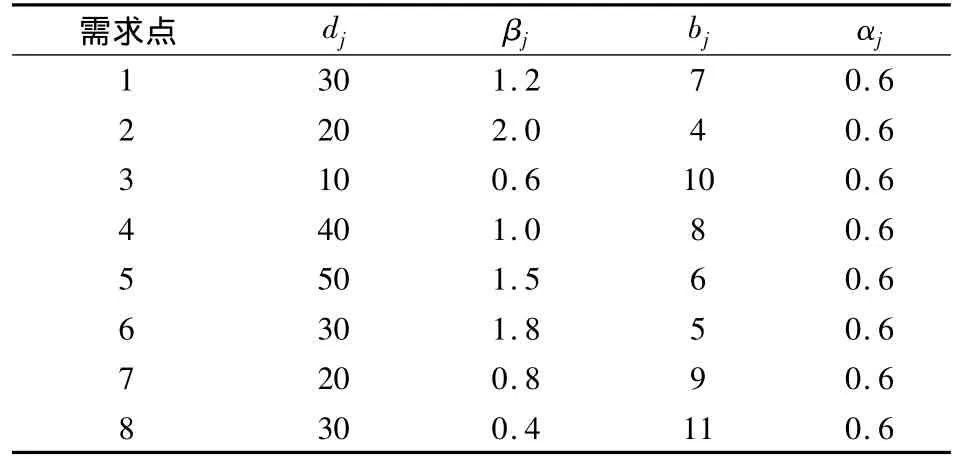
表2 需求点参数

表3 时间距离表

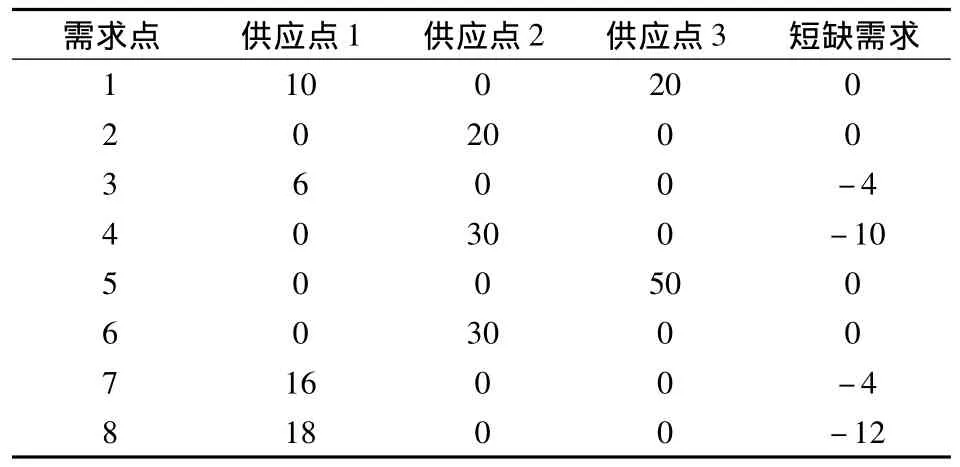
表4 上层最优解

由表4可计算得上层最优解的目标函数值为F=177.12.根据上层最优解可求得下层最优解，结果见表5.在本算例中，鉴于下层目标函数的特征，最优解不唯一.

由表5可知，最优解形成了集覆盖调度方案，即供应点1出发的车辆覆盖需求点(1，3，7，8)，供应点2出发的车辆覆盖需求点(2，4，6)，供应点3出发的车辆覆盖需求点(1，5).由此可以计算出下层目标函数最优值为0，也即无延迟发生.总的来说，该算例体现了算法中以时间窗为重要衡量标准的指派特征.基于动态规划的两阶段启发式算法，在第1阶段以满足时间窗为目标，在第2阶段以最快完成配送任务为目标，算例结果验证了算法的可行性.从管理学角度来讲，应急管理部门先行决策各供应点到需求点的最优配送量，可以提高各阶段车辆调度效率，战术层决策依赖于战略层的规划部署.鉴于本算例的特殊性，故存在一些缺陷:① 上层目标的最优解没有能够验证算法的收敛性;②算例中车辆对于时间域来讲相对充足，现实情境下车辆可能在时间域无法完成供应点的配送任务.

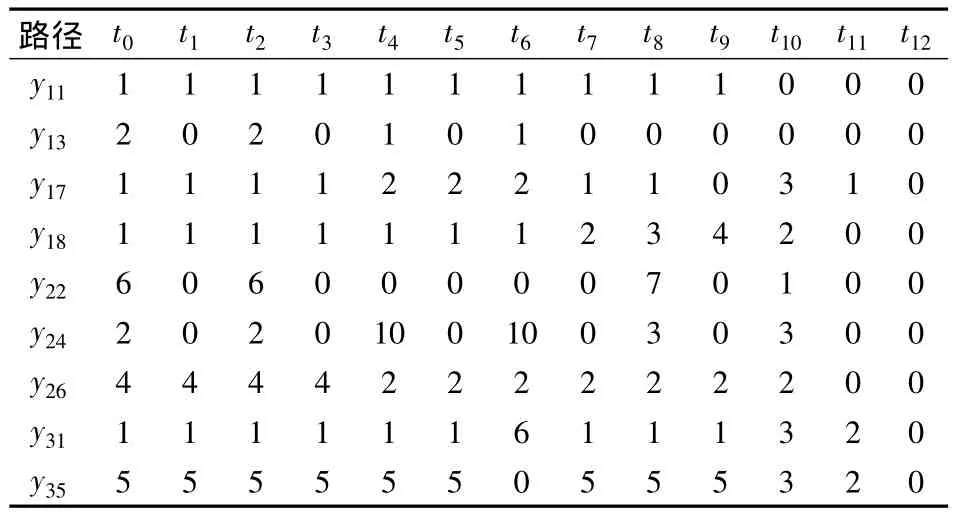
表5 车辆调度计划

4 结语

本文考虑了应急背景下车辆多次、分阶段调度以实现资源优化配置的问题.在针对多阶段应急车辆调度、车辆动态决策的研究上，这种基于双层规划的应急救援车辆调度模型表现出较大的创新性.与此同时，双层规划降低了整个问题求解的维度，算例较好地验证了双层规划算法实现全局最优的可行性.总体来说，本文提出的应急救援车辆调度优化方案拟合了现实应急情境，能够为应急管理部门的车辆调度与应急资源配置提供辅助决策.

应急情景下各类信息往往是动态的，需求的种类与数量会随着时间的变化而变化，整个应急物资配送的网络应该是一个动态网络.本文设定的应急需求与供应都是常量，在未来的研究中可以考虑物资供应是随时间而变化的.本文假定车辆返回后必须返回原出发点，而在实践中车辆可能返回任意资源供应点，可能会产生更优的解.此外，本文考虑的车辆返回是空返，为了加强应急环境下车辆使用的有效性，在未来可以考虑车辆返回时能够转移受伤人群，将应急资源配置与人群疏散结合起来.

References)

[1] Dantzing G，Ramser J.The truck dispatching problem[J].Management Science，1959，6(1):80-91.

[2] Brandão J.A tabu search algorithm for the heterogeneous fixed fleet vehicle routing problem[J].Computers＆ Operations Research，2011，38(1):140-151.

[3] Belfiore P C，Yoshizaki H T Y.Scatter search for a reallife heterogeneous fleet vehicle routing problem with time windows and split deliveries in Brazil[J].European Journal of Operational Research，2009，199(3):750-758.

[4] Bettinelli A，Ceselli A，Righini G.A branch-and-cutand-price algorithm for the multi-depot heterogeneous vehicle routing problem with time windows[J].Transportation Research Part C:Emerging Technologies，2011，19(5):723-740.

[5] Azi N，Gendreau M，Potvin J.An exact algorithm for a single-vehicle routing problem with time windows and multiple routes[J].European Journal of Operational Research，2007，178(3):755-766.

[6] Xu L Y.A heuristic algorithm for the multi-period vehicle routing problem with simultaneous pickup and delivery service[D].Hong Kong:Hong Kong University of Science and Technology，2010.

[7] Wen M，Cordeau J，Laporte G，et al.The dynamic multi-period vehicle routing problem[J].Computers＆Operations Research，2010，37(1):1615-1623.

[8] Yuan Y，Wang D W.Path selection model and algorithm for emergency logistics management[J].Computers ＆ Industrial Engineering，2009，56(3):1081-1094.

[9] Wohlgemuth S，Oloruntoba R，Clausen U.Dynamic vehicle routing with anticipation in disaster relief[J].Socio-Economic Planning Sciences，2012，46(4):261-271.

[10] 石彪，池宏，祁明亮，等.应急物资运输的两阶段车辆调度模型[J].系统工程，2012，30(7):105-111.Shi Biao，Chi Hong，Qi Mingliang，et al.A two-stage vehicle scheduling model of transportation of emergency resources[J].Systems Engineering，2012，30(7):105-111.(in Chinese)