Experimental study on desorption of soluble matter as influenced by cations in static water
2014-03-15WenshengXULiCHENXiaoxiaTONGXiaopingCHENPingcangZHANG
Wen-sheng XU*, Li CHEN, Xiao-xia TONG, Xiao-ping CHEN, Ping-cang ZHANG
1. Division of Soil and Water Conservation, Changjiang River Scientific Research Institute, Wuhan 430010, P. R. China
2. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, P. R. China
Experimental study on desorption of soluble matter as influenced by cations in static water
Wen-sheng XU*1, Li CHEN2, Xiao-xia TONG1, Xiao-ping CHEN1, Ping-cang ZHANG1
1. Division of Soil and Water Conservation, Changjiang River Scientific Research Institute, Wuhan 430010, P. R. China
2. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, P. R. China
With variation of drainage basin environments, desorption of soluble matter has become one of the significant erosion processes in rivers. It has a considerable impact on flow and sediment transport, as well as processes of river bed deformation and landform evolution throughout a watershed. In this study, considering influences on sediment movement, especially on cohesive sediment transport, Ca2+and H+were chosen as characteristic ions of soluble matter, and the total desorption quantity of Ca2+and pH value when the desorption equilibrium is reached were employed as two indexes representing the desorption of soluble matter. By means of an indoor experiment, desorption of soluble matter as influenced by cations in static water was investigated. The results show that the total desorption quantity of soluble matter increases with the initial cation concentration until a maximum desorption quantity value is obtained and maintained. The total desorption quantity of soluble matter depends on properties of the specific cations in static water, and the stronger the affinity is between the cation and sediment surface, the higher the total desorption quantity will be. Finally, a strong approximate linear relationship between desorption quantities for different kinds of soluble matters was obtained, which means that variation of pH values can accurately reflect the desorption results of soluble matter.
soluble matter; desorption; cation; sediment; static water; indoor experiment
1 Introduction
Erosion of soluble matter occurs along with sediment erosion. These are the two main erosion processes of land surfaces induced by runoff. Due to variation of the drainage basin environment, a large amount of soluble matter is eroded by water flow and transported into rivers, where it interacts with river flow, sediment transport, and river bed topography, resulting in considerable impacts on flow and sediment transport, as well as the processes of river bed deformation and landform evolution throughout the basin (Wang et al. 2009a; Xu et al. 2010; Semenov and Zimnik 2010; Reczynski et al. 2010). In China, the average erosionmodulus of soluble matter actually reaches 52 × 109kg/(km2·a) for rivers flowing into oceans, putting it at the highest level in the world (Yang et al. 2000). Therefore, substantially eroded soluble matter has become one of the important factors in river systems, and it is necessary to investigate the erosion of soluble matter.
On account of its considerable impact on water quality of rivers, soluble matter has caught the attention of many hydrochemists and geochemists around the world (Meybeck and Helmer 1989; Wang et al. 2009b; Viers et al. 2009; Hurwitz et al. 2010; Li et al. 2011; Soumya et al. 2011). However, in these studies the soluble matter was more associated with river environment evolution, rock weathering, geo-chemical cycles, and global climate change, and took less consideration of the processof erosion. In general, soluble matter mainly includes Na+, K+, Ca2+, Mg2+, Cl-, SO42-, HCO3-, CO32-, as well as a small quantity of dissolved heavy metal ions (Chen et al. 2005). According to the characteristics of soluble matter release, the erosion of soluble matter contains two kinds of processes: one is soluble matter being desorbed from sediment surfaces into water, and the other is the desorbed soluble matter subsequently being transported by water flow (Shaw 1992; Xu et al. 2009). Therefore, investigation of desorption will provide a reliable basis for further understanding the erosion mechanism of soluble matter.
In terms of hydro-chemical principles (Chen 2006), water quality is one of the most important factors in desorption of soluble matter, which has been studied by many researchers. For instance, Tran et al. (2002) compared the effects of the pH value on desorption of Cd2+in sandy soils with and without infiltration. Singh et al. (2006) investigated the desorption of Zn2+under the influences of Ca2+inthe soils of Canterbury Plain, New Zealand. Arias et al. (2005) experimentally studied the effects of the pH value and concentration of electrolytes in solutions on desorption of Cu2+and Zn2+. Nevertheless, the previous achievements mainly focused on the desorption of heavy metal ions, and the desorption conditions for heavy metal ions differed greatly from the environment of a single actual desorption process.
Water quality parameters mainly involve electrolyte type, concentration, composition in solution, and so forth. The authors have already investigated the desorption of soluble matter as influenced by Na+in static water (Xu et al. 2009). However, because of the complexity of effects of water quality on desorption, the influences of cations on desorption of soluble matter were further explored in this study through static indoor experiments. For experiments, Ca2+, which has a significant impact on movement of sediment, especially sediment with fine sizes and a high concentration in natural water bodies, and H+, which has a remarkable influence on surface charge properties of fine-size sediment, were chosen as the representative ions of soluble matter, and the total desorption quantity of Ca2+and pH values when desorption equilibrium is acquired were correspondingly employed as the two indexes representing the desorption of soluble matter. This study reasonably simulated the desorption process of solublematter, supplying a theoretical basis for understanding the erosion mechanism of soluble matter in overland flow. Moreover, it is helpful to establish an erosion model of soluble matter in overland flow and to forecast variation of the water environment in a basin.
2 Experiment design
2.1 Materials and methods
Experiments were conducted in the State Key Laboratory of Water Resources and Hydropower Engineering Science at Wuhan University. Considering that the main objective of this study was to explore the erosion mechanism of soluble matter in overland flow in the Yangtze River Basin, and soluble matter mostly comes from accumulated loose surface materials on slopes, sediment (top soil) on hillslopes was chosen for testing samples. Two kinds of sediment, A and B, were sampled from the different locations in the Yangtze River Basin. Both of them were brown red loam soil. Sampling locations (A: 30°32′36″N, 114°21′56″E; B: 30°32′12″N, 114°20′34″E) were west of Luojia Hill at Wuhan University. In the region, temperature ranges from −17.3℃ (January 31, 1969) to 41.3℃ (August 10, 1934), with an annual average temperature of around 16.8℃. The annual average precipitation is 1 284.0 mm. The southwestern monsoon brings very distinct wet and dry seasons, with the majority of precipitation falling in the summer, and an annual average moisture content of 77% (Zhou et al. 1999). The sampling locations were relatively pristine, densely vegetated, and hardly disturbed by human activities. For sampling, the surface sediments from two locations with a depth of less than 20 cm were collected after the leaves, sticks, and stones had been removed with a plastic scoop. Collected samples were stored in large plastic bags and transported to the laboratory. Before the test, the samples were naturally air dried, thoroughly mixed, and passed through a 4-mm sieve to remove the coarser particles. The pH value of sediment was considered that of a mixture with a sediment-to-deionized water mass ratio of 1:5. The pH value of the mixture was measured after shaking for one hour on an end-over-end shaker followed by one hour of equilibration. The pH values of samples A and B were 4.60 and 5.70, respectively, and the grain size distribution curves for samples A and B are shown in Fig. 1.

Fig. 1 Grain size distribution curves for sediment samples A and B
For experiments, a series of sediment samples with a mass of 100 g and 500 ml of solution were added into crystallizing dishes with volume capacities of 1 000 ml. The solution was composed of deionized water and electrolytes with a predetermined concentration. In order to reduce the impact of deionized water on the desorption of soluble matter, the deionized water was filtrated with an ultrapure-water machine before use. It was shown that the ultrapure deionized water had a pH value of 7.4 and could be considered not to contain Ca2+or H+.
Then, the dishes were placed on a magnetic stirrer and stirred for 20 minutes at the same speed, after which the dishes were sealed with plastic film and stored in a glass tank for desorption equilibration so that the soluble matter could be fully desorbed from sediment surfaces. The tank was half-filled with water whose temperature was maintained at 25℃. The equilibration time is very important in determining whether soluble matter was fully desorbed or not. In this study, the equilibrationtime was determined to be 23 hours through several iterations of experiments, which agreed with the results of previous studies (Tran et al. 2002; Arias et al. 2005; Singh et al. 2006).
After equilibration, the dishes were carefully taken out of the tank. Next, the supernatant solution in the dish was poured into a glass beaker with a volume capacity of 500 ml and collected. After filtration with a medium-speed quantitative filter paper seated on the filter holder, a clear sample solution was obtained. Then, according to the Ethylene Diamine Tetraacetic Acid (EDTA ) titration method introduced in the Monitoring and Analysis Method Guide for Water and Waste Water (Wei et al. 1997), we could easily detect the concentration of Ca2+in a predetermined volume of sample solution using an automatic potential titrator. Therefore, the total desorption amount of Ca2+could be obtained through a simple calculation, which reflected the desorption results of soluble matter. In addition, the pH value of the filtrated sample solution was detected with a portable pH measuring instrument.
2.2 Experiment parameters
The parameters used in this experiment mainly included initial concentrations and types of cations in solution. Three types of cations were used: Na+, NH4+, and H+. For each cation, we chose seven initial concentrations corresponding to the seven experimental conditions of case 1 to case 7. All parameters are presented in Table 1.

Table 1 Initial concentration of each cation in solution unit: mmol/L
3 Effects of initial cation concentrations on total desorption quantity of soluble matter
The total desorption quantity of soluble matter is an obvious indicator of the amount of soluble matter released from sediment surfaces to a solution when equilibrium between desorption and adsorption is attained on the interface of the sediment surface and solution. The pH value of a solution directly reflects the concentration of H+, with a lower pH value corresponding to a higher concentration of H+in a given volume of solution (Xu et al. 2009).
Taking Na+as an example, Fig. 2 presents the variation of the total desorption quantity of Ca2+with the initial concentration of Na+in the solution. It is observed that Ca2+is least desorbed when there is no Na+in the solution. As the initial Na+concentration increases, the total desorption quantity of Ca2+increases, and the increase rate of the desorption quantity falls. This implies that there exists a maximum desorption quantity of Ca2+as the initial Na+concentration increases. In addition, the total desorption quantity of Ca2+is higher for sample B than for sample A.
Fig. 3 shows the relationship between the initial concentration of Na+and the pH value when desorption equilibrium is achieved. It can be seen that the pH value has the greatest value when there is no Na+in the solution, and that it decreases at a falling speed with the increase of the initial concentration of Na+, with the result that the pH value tends toward a certain minimum value as the initial Na+concentration continuously increases. In addition, the pH value of sample A is generally lower than that of sample B.
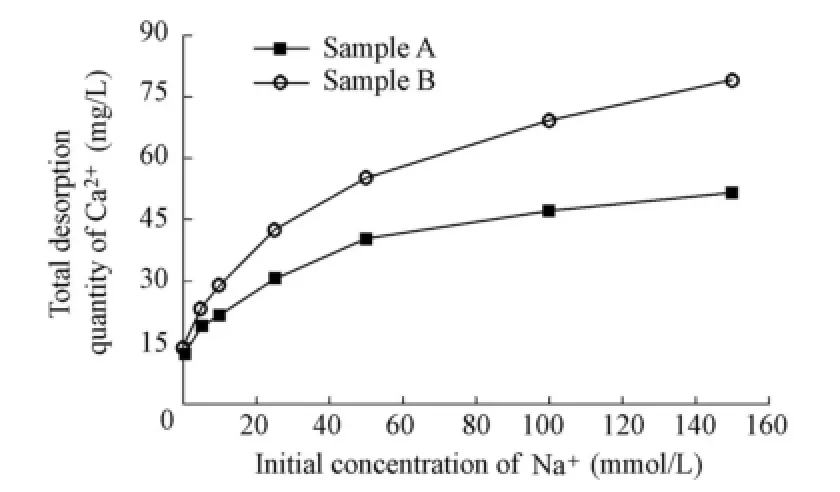
Fig. 2 Variation of total desorption quantity of Ca2+with initial Na+concentration
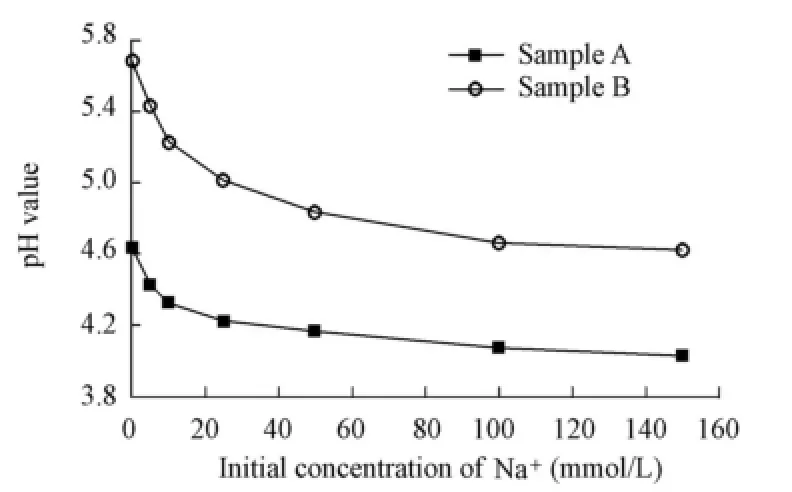
Fig. 3 Variation of pH value with initial Na+concentration
This discussion on the variation of both the total desorption quantity of Ca2+and the pH value with the initial concentration of cations in the solution is easily summarized by saying that soluble matter is least desorbed when there is no initial cation in the solution and its total desorption quantity increases at a falling speed as the initial concentration of cations increases. This is due to the desorption of soluble matter consisting of two processes: diffusion and ion exchange (Li 2001; Xu et al. 2010). In a solution that is initially without cations, soluble matter is desorbed through a process of diffusion, in which soluble matter directly diffuses from sediment surfaces into a solution due to a concentration gradient of soluble matterbetween sediment surfaces and the solution. However, as it is attracted by molecular and electrostatic attraction forces induced by the inner sediment particle core, soluble matter is consequently less desorbed.
In a solution with a low concentration of cations, the cations are found to have a greater chance of both diffusing to sediment surfaces from a solution and subsequently exchanging ions with soluble matter originally attracted on sediment surfaces when cations’ initial concentration increases. As a result, more soluble matter is desorbed from sediment surfaces and then diffused into a solution, which manifests as the total desorption quantity of soluble matter in the solution increasing. However, the total amount of exchangeable soluble matter on the sediment surfaces is finite, and the ion exchange process between the soluble matter originally adsorbed on the sediment surfaces and the cations in a solution is reversible, so, as the soluble matter is continually exchanged, the exchange intensity gradually weakens. As a result, it can be seen that the total desorption quantity of soluble matter gradually increases to a maximum constant amount at a falling speed, with the increase of the initial concentration of cations in the solution.
4 Effects of different cations on total desorption quantity of soluble matter
When soluble matter is naturally desorbed into overland flow, more than one type of cation is usually contained in the water body at the same time, with each type having individual special chemical properties, inducing different influences on the desorption process, and consequently causing different effects on the total desorption quantity of soluble matter. This is discussed below.
Because the results of sediment samples A and B are similar, only one of them is randomly selected for illustration here. As an example, Fig. 4 shows the relationship between the total desorption quantity of Ca2+released from sediment sample A and the initial concentration of different types of cations. It can be seen that there is a similar variation of the total desorption quantity of Ca2+with the initial concentration of different types of cations. At the same initial concentration, the total desorption quantity of Ca2+differs for different types of cations, with the highest total desorption quantity of Ca2+in the solution with H+, and the lowest one in the solution with Na+.
Fig. 5 shows the variation of the pH value with the initial concentrations of different types of cations when desorption equilibrium is attained. It can be observed that the pH value still has a similar variation profile with the initial concentrations of different types of cations. At the same initial concentration, the pH value is highest in the solution with Na+, and lowest in the solution with H+. As the initial concentration of cations increases, the difference in the pH value between the solutions with different types of cations increases, and, finally, a constant value is maintained between the solutions with Na+and NH4+.
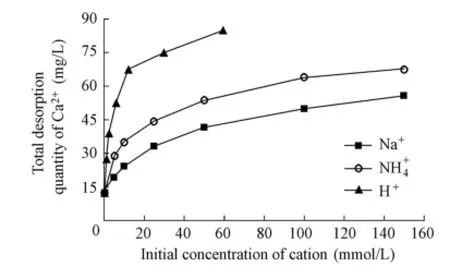
Fig. 4 Variation of total desorption quantity of Ca2+with initial concentration of different kinds of cations

Fig. 5 Variation of pH value with initial concentration of different kinds of cations
In order to further explore the effects of cation type on the desorption of soluble matter, the variation of the total desorption amount of soluble matter with the initial concentration of different cations was fitted with the Langmuir equation, which is mostly used with high precision (Tran et al. 2002; Arias et al. 2005; Xu et al. 2010). The Langmuir equations for the total desorption amount of Ca2+and pH value are as follows:

where C is the initial concentration of cations in solution (mmol/L), T is the total desorption quantity of Ca2+(mg/L), P is the pH value, Tmaxis the maximum desorption amount of Ca2+(mg/L), Pminis the minimum pH value, K1is the desorption coefficient, and K2is the equilibrium coefficient .
Table 2 shows the fitted parameters of Eq. (1) and Eq. (2). From the fitted results it can be seen that the maximum desorption amount of Ca2+is different for different types of cations, with an ascending order of Na+, NH4+, to H+, which is similar to the variation of desorption coefficients, but is entirely opposite to the variation of the minimum pH value. The results given in Table 2 are in considerably good agreement with those presented in both Fig. 4 and Fig. 5.

Table 2 Fitted parameters of Eq. (1) and Eq. (2)
Desorption coefficient K1and equilibrium coefficient K2are two extremely significant factors influencing the total desorption quantity of Ca2+and the pH value when desorption equilibrium is reached. They are dominated by the properties of soluble matter, cation type, sediment characteristics, and the interface action between sediment and solution (Li 2001). Inour experiment K1and K2were mainly determined by the type of cations contained in the solution. The hydrochemistry properties of Na+, NH4+, and H+are remarkably different. As a result, the desorption coefficient K1and equilibrium coefficient K2present considerable variation along with the cation type.
From the analysis above it can be concluded that the total desorption quantity of soluble matter has similar variation with the initial concentration of cations for both different sediment samples and various types of cations. However, the total desorption quantity of soluble matter is entirely different for various types of cations, with the result that the desorption amount is highest in the solution with H+, lowest in the solution with Na+, and in between the two former values in the solution with NH4+, due to the diversity of affinity between the cation and sediment surface. The affinity differs for different cations because of the difference of their special hydrated ionic radii, which results in the number of cations joining in the exchange with soluble matter being different, and then adifferent amount of soluble matter being desorbed for different cations (Shaw 1992). According to Li’s experimental results (Li 2001), the affinity for H+, NH4+, and Na+with sediment surfaces follows an order of H+〉 NH4+〉Na+, which leads to the same order of the influences on the total desorption quantity of soluble matter. Therefore, the stronger the affinity is, the greater the ability of cations to exchange ions with the soluble matter originally adsorbed on sediment surfaces, which can subsequently cause more soluble matter to be released into the solution: a stronger affinity will give rise to a higher total desorption quantity of soluble matter.
5 Analysis of relationship between total desorption quantity of soluble matter and pH value
Natural sediment surfaces are covered by many types of soluble matter. When desorption is complete, a dynamic equilibrium between desorption and adsorption of soluble matter on the interfaces between the sediment surface and solution will be obtained, which subsequently induces the existence of a certain quantitative relationship among the total desorption amounts for different types of soluble matter.
Fig. 6 presents the variation of the pH value against the total desorption quantity of soluble matter for (a) different sediment samples with a cation type of Na+and (b) different types of cations with sediment sample A. As shown in Fig. 6, the pH value decreases with the increase of the total desorption quantity, irrespective of the sediment sample type and cation type. The pH value was observed to have similar variation with the total desorption amount of soluble matter for different sediment samples (Fig. 6(a)), resulting in sediment sample A being randomly selected to be further analyzed as an example (Fig. 6(b)). Fig. 6(b) shows that the rate of decrease of the pH value changes dependingon the specific cation type. The figure also shows that, as the total desorption quantity of Ca2+increases, the pH value decreases at a falling rate in the solutions with Na+and NH4+, and it decreases at an approximately invariable rate in the solution with H+. With the same total desorption amount of Ca2+, the difference inpH values for different types of cations is negligible with a low desorption amount of Ca2+, whereas it gradually increases when the total desorption quantity of Ca2+increases. During this process, the difference in pH value between the solutions with Na+and NH4+cations gradually increases and finally stabilizes. With a high total desorption amount of Ca2+, the pH value is greatest in the solution with Na+, lowest in the solution with H+, and in between these two values in the solution with NH4+.
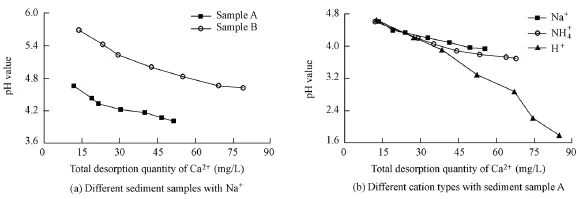
Fig. 6 Variation of pH value with total desorption quantity of Ca2+
To further examine the relationship between the total desorption quantity of soluble matter and the pH value, a regression analysis was conducted. The regression equation we used is as follows:
《公约》要求各缔约国采取强有力的措施,保障举报人的安全。但我国现有关于举报人保护的法律规定过于原则,不利于保护举报人。因此,亟需作出专门保护举报人的如下规定:第一,在检察机关、公安机关内部成立专门的举报人保护机构并明确其职责;第二,完善对举报人损害补偿制度,应至少包括举报人为举报所支付的交通费、住宿费、生活费等相关费用。而且“对举报人直接或间接损失的补偿支出,应列入国家财政予以保障”。[13]

where T′ is the logarithm of the total desorption quantity of Ca2+, and a and b are coefficients.
The results are shown in Table 3. It can be seen that the logarithm of total desorption quantity of Ca2+has a strong linear relationship with the pH value, and the correlation coefficients (r2) between T′ and P are mostly greater than 0.99, except for H+, where r2= 0.86. This proves that desorption of Ca2+and H+are two companion processes. It can be concluded that the variation of the pH value can accurately represent the desorption quantity of soluble matter.

Table 3 Parameters of fitted equations used for simulating relationship between pH value and desorption quantity of Ca2+
Based on these analyses, it can be concluded that, under influences of cations, the desorption processes for different types of soluble matter originally adsorbed on sediment surfaces occur simultaneously, and that they correlate with one another. This is not surprising, because for any specific cation there is a similar chance of diffusing to different adsorption sites on sediment surfaces. Thus, for different cations, there is a similar chance of a specificcation exchanging with different types of soluble matter originally adsorbed on sediment surfaces, which results in a strong correlation between desorption processes of different types of soluble matter. Nevertheless it should be noted that competition for desorption exists, and the exchange energy for different types of soluble matter changes with cations, meaning that the chances for different types of desorbed soluble matter to be adsorbed to sediment surfaces again are different. Therefore, in the same desorption environment, different types of soluble matter will show different desorption amounts.
6 Conclusions
As one of the significant erosion processes in rivers, desorption of soluble matter has considerable influence on flow and sediment transport. In order to understand the erosion mechanism of soluble matter from sediment in overland flow, based on indoor experiments on desorption of soluble matter as influenced by cations in static water, the following conclusions can be drawn:
(1) The higher the initial concentration of cations is in the solution, the larger the total desorption quantity of soluble matter will be. A maximum value of the total desorption quantity of soluble matter will be reached asymptotically.
(2) The type of cations has a considerable effect on the total desorption quantity of soluble matter. The stronger the affinity is between cations and sediment surfaces, the higher the total desorption quantity of soluble matter will be. The experimental results show that the total desorption quantity of Ca2+for H+, NH4+, and Na+follows an order of H+〉 NH4+〉 Na+.
(3) Strong correlation was observed for the desorption processes of different types of soluble matter, as exemplified by the relation between the pH value and the total desorption quantity of Ca2+, although the total desorption quantity varies from one to another. As the total desorption quantity of soluble matter increases, the pH value decreases. This suggests that the variation of the pH value can be used to represent the extent and quantity of desorption of soluble matter.
While soluble matter is naturally desorbed in overland flow with dynamic water environments, the present experiments were only conducted in static water conditions, without consideration of the action of water flow. Therefore, further investigation of desorption of soluble matter as influenced by dynamic water flow is warranted.
We wish to thank Dr. Hu Peng of Zhejiang University, China for his valuable suggestions.
Arias, M., Pérez-Novo, C., Osorio, F., López, E., and Soto, B. 2005. Adsorption and desorption of copper and zinc in the surface layer of acid soils. Journal of Colloid and Interface Science, 288(1), 21-29. [doi: 10.1016/j.jcis.2005.02.053]
Chen, J. S., Wang, F. Y., Meybeck, M., He, D. W., Xia, X. H., and Zhang, L. T. 2005. Spatial and temporal analysis of water chemistry records (1958-2000) in the Huanghe (Yellow River) basin. GlobalBiogeochemical Cycles, 19(3), 1-24 (GB3016). [doi:10.1029/2004GB002325]
Chen, J. S. 2006. Principle of Water Quality in Rivers and Water Quality of Rivers in China. Beijing: Science Press. (in Chinese)
Hurwitz, S., Evans, W. C., and Lowenstern, J. B. 2010. River solute fluxes reflecting active hydrothermal chemical weathering of the Yellowstone Plateau Volcanic Field, USA. Chemical Geology, 276(3-4), 331-343. [doi:10.1016/j.chemgeo.2010.07.001]
Li, S. Y., Lu, X. X., He, M., Zhou, Y., Bei, R. T., Li, L., and Ziegler, A. D. 2011. Major element chemistry in the upper Yangtze River: A case study of the Longchuanjiang River. Geomorphology, 129(1-2), 29-42. [doi:10.1016/j.geomorph.2011.01.010]
Li, X. Y. 2001. Soil Chemistry. Beijing: Higher Education Press. (in Chinese)
Meybeck, M., and Helmer, R. 1989. The quality of rivers: From pristine stage to global pollution. Palaeogeography, Palaeoclimatology, Palaeoecology, 75(4), 283-309. [doi:10.1016/0031-0182 (89)90191-0]
Reczynski, W., Jakubowska, M., Golas, J., Parker, A., and Kubica, B. 2010. Chemistry of sediments from the Dobczyce Reservoir, Poland, and the environmental implications. International Journal of Sediment Research, 25(1), 28-38. [doi:10.1016/S1001-6279(10)60025-X]
Semenov, M. Y., and Zimnik, E. A. 2010. Use of chemical composition of surface waters in estimating contributions from dissolved matter sources. Geography and Natural Resources, 31(2), 170-176. [doi: 10.1016/j.gnr.2010.06.013]
Shaw, D. J. 1992. Introduction to Colloid and Surface Chemistry. 4th ed. New York: Elsevier Scientific Publishing Company.
Singh, D., McLaren, R. G., and Cameron, K. C. 2006. Zinc sorption-desorption by soils: Effect of concentration and length of contact period. Geoderma, 137(1-2), 117-125. [doi:10.1016/j.geoderma. 2006.08.002]
Soumya, B. S., Sekhar, M., Riotte, J., Audry, S., Lagane, C., and Braun, J. J. 2011. Inverse models to analyze the spatiotemporal variations of chemical weathering fluxes in a granito-gneissic watershed: Mule Hole, South India. Geoderma, 165(1), 12-24. [doi:10.1016/j.geoderma.2011.06.015]
Tran, Y. T., Barry, D. A. and Bajracharya, K. 2002. Cadmium desorption in sand. Environment International, 28(6), 493-502. [doi:10.1016/S0160-4120(02)00077-6]
Viers, J., Dupré, B., and Gaillardet, J. 2009. Chemical composition of suspended sediments in World Rivers: New insights from a new database. Science of the Total Environment, 407(2), 853-868. [doi: 10.1016/j.scitotenv.2008.09.053]
Wang, J. S., Chen, L., Fan, B. L., and Chai, X. L. 2009a. Relationship between ion transport and sediment discharge in river. Advances in Water Science, 20(5), 658-662. (in Chinese)
Wang, R. M., You, C. F., Chu, H. Y., and Hung, J. J. 2009b. Seasonal variability of dissolved major and trace elements in the Gaoping (Kaoping) River Estuary, Southwestern Taiwan. Journal of Marine Systems, 76(4), 444-456. [doi:10.1016/j.jmarsys.2007.11.012]
Wei, F. S. 1997. Monitoring and Analysis Method Guide for Water and Wastewater. Beijing: China Environmental Science Press. (in Chinese)
Xu, W. S., Chen, L., Liu, J., and Jiang, L. 2010. Analysis on models for predicting the desorption quantity of soluble matters in rivers. Journal of Sichuan University (Engineering Science Edition), 42(4), 42-47. (in Chinese)
Xu, W. S., Chen, L., Zhao, D. Z., and Liu, X. T. 2009. Experimental study of the effects of Na+on the desorption of soluble chemicals in rivers. Advances in Water Science, 20(4), 537-543. (in Chinese)
Yang, S. Y., Liu, S. G., and Li, C. X. 2000. Chemical fluxes of asian rivers into the ocean and their controlling factors. Marine Science Bulletin, 19(4), 22-28. (in Chinese)
Zhou, J., Liu, G. H., Pan, M. Q., Zhai, B., and He, J. L. 1999. Study on vegetation and its succession on Luojia Hill, Wuhan, Wuhan I: Status quo of vegetation. Plant Science Journal, 17(3), 231-238. (in Chinese)
(Edited by Yan LEI)
This work was supported by the National Natural Science Foundation of China (Grant No. 51209014) and the Fundamental Research Funds for the Changjiang River Scientific Research Institute (Grant No. CKSF2013012/TB).
*Corresponding author (e-mail: wenshengxu521@aliyun.com)
Received Sep. 16, 2013; accepted Sep. 1, 2014
猜你喜欢
杂志排行
Water Science and Engineering的其它文章
- Water Science and Engineering ISSN 1674-2370, CN 32-1785/TV Vol. 3, Nos.1-4 2010 TOTAL CONTENTS
- Design formulas of transmission coefficients for permeable breakwaters
- Sea level change under IPCC-A2 scenario in Bohai, Yellow, and East China Seas
- Simulation-optimization model of reservoir operation based on target storage curves
- Comparison between dynamic programming and genetic algorithm for hydro unit economic load dispatch
- Optimal early refill rules for Danjiangkou Reservoir