Comparison between dynamic programming and genetic algorithm for hydro unit economic load dispatch

Bin XU, Ping-an ZHONG*,, Yun-fa ZHAO, Yu-zuo ZHU, Gao-qi ZHANG

1. College of Hydrology and Water Resources, Hohai University, Nanjing 210098, P. R. China

2. National Engineering Research Center of Water Resources Efficient Utilization and Engineering Safety, Hohai University, Nanjing 210098, P. R. China

3. China Three Gorges Corporation, Beijing100038, P. R. China

4. Datang Yantan Hydropower Corporation, Nanning 530022, P. R. China

5. Yellow River Engineering Consulting Co., Ltd., Zhengzhou 450003, P. R. China

Comparison between dynamic programming and genetic algorithm for hydro unit economic load dispatch

Bin XU1, Ping-an ZHONG*1,2, Yun-fa ZHAO3, Yu-zuo ZHU4, Gao-qi ZHANG5

1. College of Hydrology and Water Resources, Hohai University, Nanjing 210098, P. R. China

2. National Engineering Research Center of Water Resources Efficient Utilization and Engineering Safety, Hohai University, Nanjing 210098, P. R. China

3. China Three Gorges Corporation, Beijing100038, P. R. China

4. Datang Yantan Hydropower Corporation, Nanning 530022, P. R. China

5. Yellow River Engineering Consulting Co., Ltd., Zhengzhou 450003, P. R. China

The hydro unit economic load dispatch (ELD) is of great importance in energy conservation and emission reduction. Dynamic programming (DP) and genetic algorithm (GA) are two representative algorithms for solving ELD problems. The goal of this study was to examine the performance of DP and GA while they were applied to ELD. We established numerical experiments to conduct performance comparisons between DP and GA with two given schemes. The schemes included comparing the CPU time of the algorithms when they had the same solution quality, and comparing the solution quality when they had the same CPU time. The numerical experiments were applied to the Three Gorges Reservoir in China, which is equipped with 26 hydro generation units. We found the relation between the performance of algorithms and the number of units through experiments. Results show that GA is adept at searching for optimal solutions in low-dimensional cases. In some cases, such as with a number of units of less than 10, GA’s performance is superior to that of a coarse-grid DP. However, GA loses its superiority in high-dimensional cases. DP is powerful in obtaining stable and high-quality solutions. Its performance can be maintained even while searching over a large solution space. Nevertheless, due to its exhaustive enumerating nature, it costs excess time in low-dimensional cases.

hydro unit; economic load dispatch; dynamic programming; genetic algorithm; numerical experiment

1 Introduction

The economic load dispatch (ELD) is one of the major functions in automatic generation control (AGC), in which the objective is to meet the required load at the least cost through optimal load dispatch among units. It is of great importance in saving energy and reducing emission. Algorithms for solving ELD problems, including mathematical programming, stochastic optimization algorithms and hybrid algorithms (Bahmanifirouzi et al. 2012;Hemamalini and Simon 2011; Somasundaram et al. 2006), have received increasing attention in recent years.

Most studies have developed conventional mathematical programming methods in early stages (Yamin 2004). Of these achievements, the equal lambda approach prevailed for a certain period of time due to its simplicity and computational advantages. However, it requires the cost function to be continuous and differentiable, and this requirement is hard to meet as the feasible range of unit power output is usually discontinuous considering the impact of the prohibited operation zone. Later, the Lagrangian relaxation (Benhamida and Abdelbar 2010; Ngundam et al. 2000) was introduced. It relaxes the load balance constraint using a Lagrange multiplier, and converges to the optimal solution through a multiplier-modifying procedure. Nevertheless, a duality gap (Ongsakul and Petcharaks 2004) might block it from reaching the global optimum. Besides, both the initialization and iteration formulation have important roles in leading to convergence. In recent years, dynamic programming (DP) (Howard 1960) has become the most widely used algorithm for ELD. However, DP suffers from the curse of dimensionality; that is, its computation expense grows exponentially with the dimensionality of the problem. To avoid the curse of dimensionality, Liang and Glover (1992) applied incremental dynamic programming (IDP) to ELD. IDP reduces the size of required memory, but is unable to guarantee a global convergence. Yang (1995) proposed dimension-reduction dynamic programming that includes offline initialization and online dispatching. The initialization synthesizes the units of the same type to an equivalent virtual unit and provides the optimal cost curve for that virtual unit before the online dispatching. After that, the required load is dispatched among the virtual units first. Then, the dispatched load on the virtual units is reallocated to each real unit. A significant problem of DP and its modified versions is seeking a compromise between the solution quality and the computation expense.

Increasing numbers of studies have tried to use stochastic algorithms to solve ELD problem (Coelho and Mariani 2009; Sinha et al. 2003). The genetic algorithm (GA) (Holland 1975) is a commonly used stochastic algorithm due to its advantages in global optimization and parallelism. However, it has the deficiencies of poor local searching ability and premature convergence. In order to overcome these deficiencies, Hrstka and Kucerov (2004) proposed the concept of a radiation zone. Radiation zones are defined as adjacent regions of local optimums. If some chromosomes are trapped in these zones, their mutation probability will increase suddenly, which helps them to jump out the local optimum. Ongsakul and Ruangpayoongsak (2001) added a simulated annealing operator to GA to refine the elitist solutions and conducted numerical experiments to dispatch the load among 40 units. The results show that, although the quality of solutions has been improved, they require excessive computation time. Li et al. (1997) presented a hybrid GA combined with the gradient method, and validated its effectiveness in a 25-unit case.

Assessing the performance of each available method for solving the ELD problem is animportant issue. Although some studies have examined the performance of GA and DP, no consensus has been reached. Baskar et al. (2003) made a comparison between DP and a modified GA in a 10-unit system. The modified GA, which incorporates a shrinking solution space technique, outperforms DP in solution quality. Orero and Irving (1996) employed a binary code GA considering a crowd mechanism. The numerical results indicate that the modified GA is inferior in solution quality to DP for a 15-unit ELD problem. Bakirtzis et al. (1994) conducted numerical experiments in a system including 72 units. The results of the experiments show that GA is always superior in CPU time in all cases, but the convergence ratio and solution quality will decrease when the number of units surpasses 18. However, these conclusions necessitate further validation for the following reasons: First, the evaluation indexes in these studies were insufficient. Basically, they should at least include the following terms: CPU time, solution quality, and convergence ratio, which are used for assessing the computation expense, optimizing ability, and stability of algorithms, respectively. In addition, these experiments were not conducted in the same simulation environment (with the same experimental scheme, programming techniques, or computer hardware and software conditions), which is the major reason for the diversity of conclusions.

In this study, we formulated the ELD problem and used DP and GA, respectively, to solve it. For comparing the performances of the two algorithms, we introduced two experimental schemes and conducted numerical experiments. We applied the methodology to the Three Gorges Reservoir. Finally, we assessed the performance of DP and GA in different dimensions of the ELD problem through numerical experiments.

2 Hydro unit economic load dispatch

(1) Objective function:

The objective of ELD is to minimize the operating cost through optimal load dispatching among units. The operating cost for a hydropower station is usually evaluated by the power release. Therefore, the objective function can be expressed as

(2) Constraints:

System load balance:

Unit power output limits:

where Q is the total power release from the reservoir (m3/s); n is the number of units; qi(⋅) is the power release of turbine unit i (m3/s), and is specifically obtained through interpolation using the power output curve of unit i; Niis the power output of unit i (MW); H is theaverage water head (m); Ndis the required load (MW); Nimax(H ) is the maximum power output of unit i at water head H (M W);Ni,jand Ni,jdenote the lower bound and upper bound of power output of unit i in the jth prohibited zone of Ωi( H) (MW), respectively; and Ωi( H) is the set of prohibited zones of unit i at water head H.

3 Methodology

3.1 Dynamic programming

By introducing the principle of optimality, DP converts a mathematical model into a multi-stage decision-making problem. In this study, DP included the following steps:

(1) Determining stage and state variables:

We selected the sequence number of unit (i) as the stage variable, and set the accumulated power output of unitsas the state variable. The accumulated power output is discretized with the increment of dN:

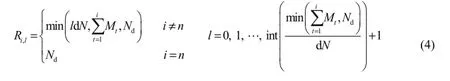
where Ri,lis the value of the lth state variable at stage i, Mtis the designed capacity of unit t, and int(⋅) is the Gaussian rounding function.

(2) Constraint handling:

We used a penalty function to handle the power output constraint. It penalizes the objective function of infeasible solutions by adding extra discharge terms into the objective function:

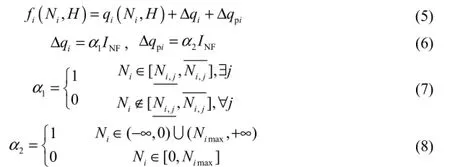
where fi(Ni, H )is the synthetic discharge of unit i at water head H (m3/s), Δqiis the penalty term for incre asing the discharge of unit i if its power output violates the prohibited zone constraint (m3/s), Δqpiis another penalty term if the power output of unit i violates the power output limit constraint (m3/s), α1and α2are binary coefficients, and INFis an extremely large coefficient (m3/s).

(3) Recursive equation:

The changing of status from stage i-1 to stage i can be characterized using the following equation:

The value of accumulated power release from unit 1 to i is updated using a forward recursive function

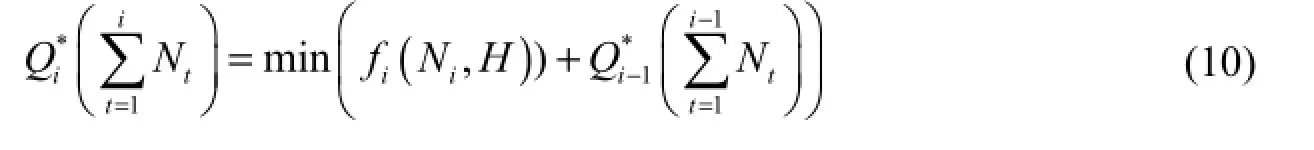
3.2 Genetic algorithm

To keep in accordance with DP in a similar solution space, an integer-coded GA was used in this study.

3.2.1 Constraints handling

The penalty function method (Chiang 2007; Kumar and Naresh 2009) and operator modification method (Michalewicz and Janikow 1996) are two conventional constraint-handling techniques. With the introduction of penalty functions, the original constrained optimization problem can be turned into an unconstrained problem. Unlike the penalty function method, the operator modification method is designed to make infeasible solutions feasible, which turns out to be a more efficient way of generating feasible solutions.

We combined the two techniques in the integer-coded GA. The operator modification method was used to handle the load balance constraint and unit power output constraint, while the penalty function method was used to deal with the prohibited zone constraint as given by Eq. (3).

3.2.2 Procedures

(1) Encoding and decoding:

We discretized the accumulated power output using Eq. (4) with an increment of dN'. pk,i(k =1,2,… ,Pop; i =1,2,… ,n ) is defined as the ith gene of the kth chromosome, where Popis the population size. pk,irepresents the column index of the accumulated power output matrixcan be used to get the accumulated power output of units 1 to i from R, as given by:

(2) Chromosome initialization:

To ensure the efficiency of the algorithm in producing feasible solutions, we used aheuristic method introduced by Zheng et al. (2013) to initialize the power output series. This method ensures that the load balance and power output limit constraints are strictly obeyed, using some linear transformation procedures during the initialization process.

(3) Fitness function:

The fitness function is used for evaluating the performance of a chromosome. Usually, a superior chromosome has a larger fitness function value. The fitness function Fitis given by

(4) Crossover operator:

The arithmetic crossover is used and can be characterized as

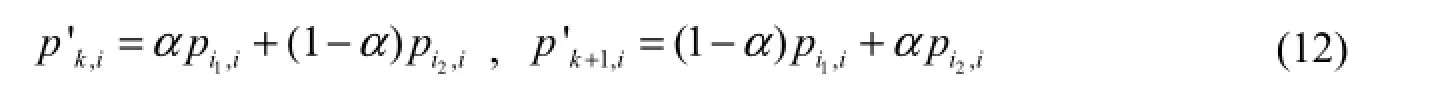
where pi1,iand pi2,iare the ith genes of the i1th and i2th parent chromosomes, respectively, and are selected to perform a crossover with the crossover probability Pc; p'k,iand p'k+1,iare the ith genes of the kth and (k+1)th child chromosomes, respectively; and α is a uniform random number in the range between 0 and 1.

(5) Mutation operator:

The mutation operator usually serves as a local search technique for the GA. A specific designed heuristic approach (Zheng et al. 2013) was used to facilitate the efficiency of GA in searching out the feasible space. The mutation probability is Pm.

(6) Selection operator:

We used the tournam ent selection to select those superior chromosomes from the entire chromosome set. After that, the selected ones were guided into the next generation, until the stopping criteria were met.

(7) Stopping criteria:

The algorithm stops when the number of generations in which the best chromosome remains unchanged is greater than a threshold (Snum) or the total number of generations reaches its expected value (Gen).

4 Numerical experimental schemes

4.1 Performance metrics

Three indices were selected for assessing the performances of DP and GA: the difference between objective functions, the difference between CPU times, and the convergence ratio. Note that the results of DP were selected as the benchmark, against which the differences were evaluated.

(1) Difference between objective functions:

We used the difference between the objective function values obtained by the GA and DP to assess the optimization ability, which is given by

where ODPand OGAare the optimal objective function values (in m3/s) obtained by DP and GA, respectively. If ΔPC＞0, this demonstrates that DP outperforms the GA in solution quality. Otherwise, GA outperforms DP.

(2) Difference between CPU times:

where TDPand TGAare the CPU times (in s) of DP and GA, respectively.

(3) Convergence ratio of GA:

The convergence ratio is an index for illustrating the robustness of a stochastic algorithm. It equals the number of successful trials divided by the total number of trials:

where nTis the total number of trials, and nSis the number of successful trials. When the optimal solution of GA is close to any one of optimal solutions of DP within a given tolerance, it is defined as a successful trial:

where NDPis one of the optimal solutions obtained by DP and recorded in the optimal solution set of DP ΨDP, NGAis the optimal solution obtained by GA, and ε is the tolerance.

4.2 Steps for numerical experiments

In general, the quality of the optimal solution obtained by an algorithm can be improved by increasing the CPU time. For instance, GA may obtain a better solution if a larger population size is provided or a larger number of generations is given. Likewise, DP can obtain a better solution on the condition that the solution space is discretized with a smaller increment. Therefore, in consideration of the fairness principle, evaluation of simulations involving an efficiency comparison should concern both the solution quality and CPU time (Cheng et al. 2009; Panigrahi et al. 2008). Accordingly, we established two schemes:

(1) Scheme A: comparing the CPU times required to obtain identical solutions.

We set the increment of GA equal to that of DP, so that the two algorithms had the same solution spaces. We then solved the problem using DP, and adjusted GA parameters to obtain the same solution as what DP found. Since the population size was the most sensitive factor of GA (Zhong and Tang 2010), we calibrated it carefully by introducing some predefined criteria. After we solved the same model using a calibrated GA, we compared the difference between CPU times.

(2) Scheme B: comparing the solution quality values within the same CPU time.

We solved the ELD problem with DP and recorded its CPU time. Then, we controlled the CPU time of GA; that is, we stoped GA when it consumed the same amount of time as DP.

Note that the increment of GA in scheme B needed to be smaller than that in scheme A. Otherwise, GA could not obtain a better solution than DP.

5 Case study

Numerical experiments were conducted using the case of the Three Gorges Reservoir in China. The Three Gorges Reservoir, which is located in the middle reach of the Yangtze River, is one of the largest water conservancy projects in the world. It has an effective storage capacity of 1.65 × 1010m3in order to regulate an average annual runoff of 4. 510 × 1011m3. The Three Gorges Reservoir has 26 hydro units of five different types, and generates 8.47 × 107MW·h of electric power annually. The characteristics of the Three Gorges Reservoir are given in Table 1.

Table 1 Characteristics of hydro units of Three Gorges Reservoir

We set the increments of both DP and GA to be 14 MW for scheme A. For scheme B, the increment of GA was set to be 1.4 MW. In addition, parameters determining GA’s performance were optimized with the trial and error method. As a result, the crossover probabilitycP was 1, the mutation probability Pmwas 0.1, and the convergence threshold Snumwas 5. We set the expected number of generations Genat 100, and the tolerance ε at 2dN n. Other parameters associated with different schemes were set as follows:

(1) For scheme A, the lower bound of the convergence ratio CRewas set at 40%. (2) For scheme B, the population size satisfied the condition Pop=5n.

5.1 Model validation

We selected a typical day from the historical records of the Three Gorges Reservoir. We conducted two set of experiments, where the required load Ndwas set as the peak load and off-peak load of that day, respectively. We ran the model for each of the required loads to find the optimal dispatch. Table 2 lists the results. The mean CPU times of DP and GA are 213.5 s and 169.3 s, respectively.

The simulated results show the following:

(1) For the off-peak load, both DP and GA have reached the same objective function value (6 331 m3/s), but the solutions of DP and GA are not the same. There are multiple optimal solutions to the ELD problem.

Table 2 Optimal load dispatch for a peak and off-peak load of a typical day

(2) For the peak load, although GA obtains a larger objective function value (6 756 m3/s) than DP (6 749 m3/s), GA consumes less CPU time. Therefore, there can be a tradeoff between solution quality and CPU time. To analyze the efficiency of algorithms, we have to conduct comparisons systematically through numerical experiments.

5.2 Results from numerical experiments

We ran the model repetitively in the Windows XP operating system using Visual Basic 6.0 programs. The computer was equipped with an Intel Core 2 Duo E7500 CPU and 2 GB of RAM. The results are listed in Table 3 and through Fig. 1 to Fig. 3.

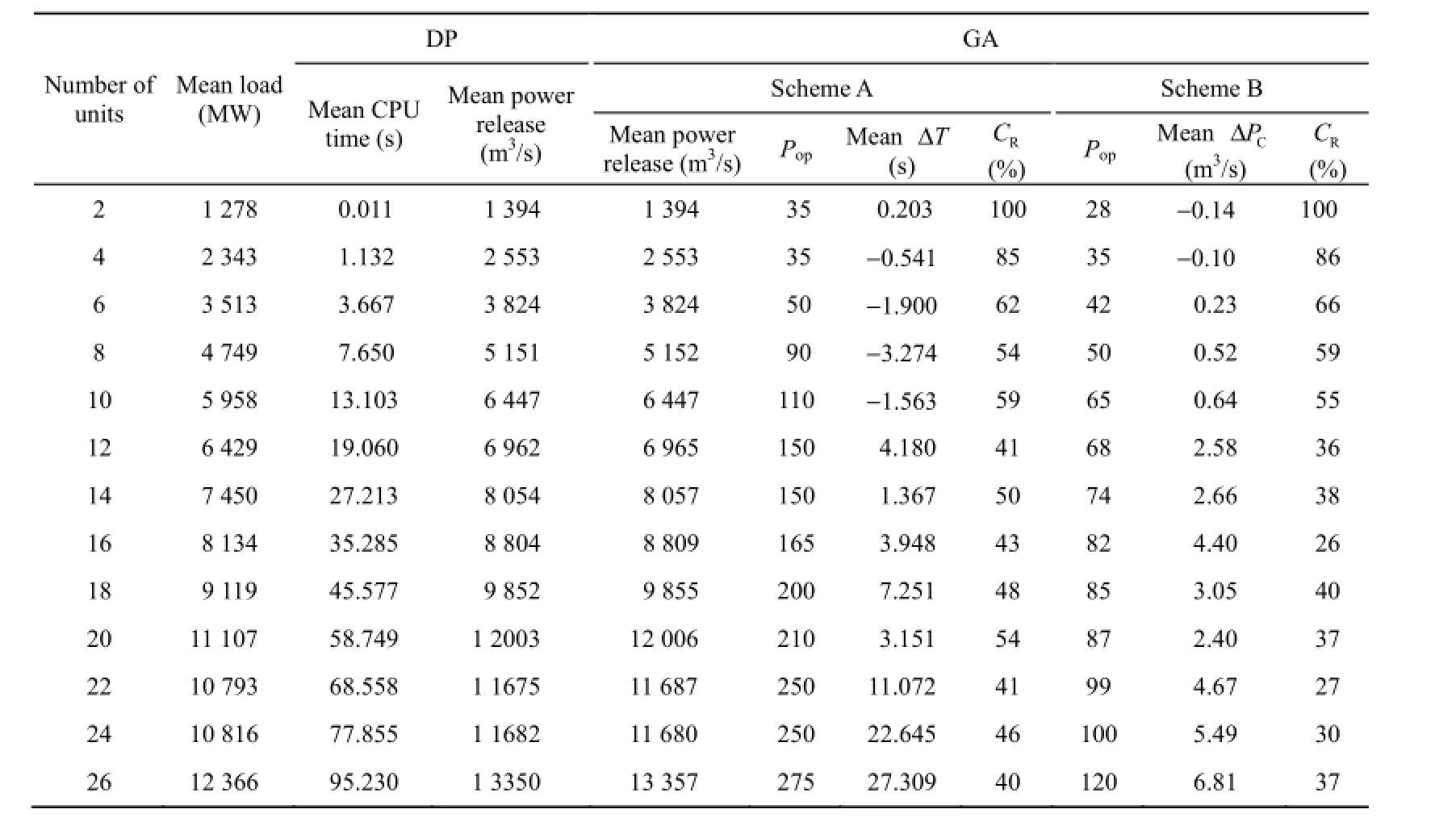
Table 3 Results of performance metrics from numerical experiments

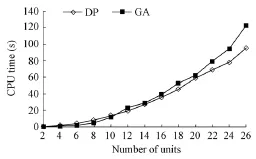
Fig. 1 CPU times of algorithms for scheme A

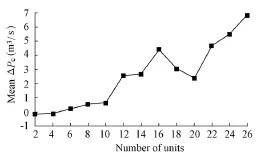
Fig. 2 Median value of difference of objective functions for scheme B

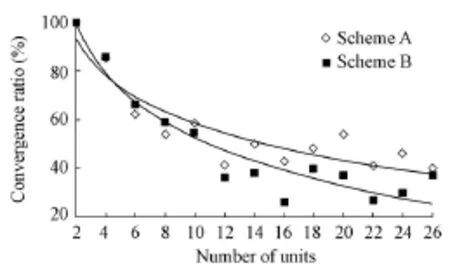
Fig. 3 Convergence ratio of solution obtained by GA for two schemes

From the results, the following can be inferred:

(1) According to Fig. 1, given the condition that the two algorithms acquire identical solutions, GA outperforms DP in CPU time when the number of units is less than 10. Otherwise, the results are reversed.

(2) As shown in Fig. 2, on the condition that the two algorithms consume the same CPU time, GA can obtain a better solution than DP if the number of units is less than or equal to 4.However, the performance of GA is inferior to that of DP with the increase of the number of units, especially when the number of units is greater than 10.

(3) As Fig. 3 shows, the convergence ratio of GA decreases with the increase of the number of units in both schemes. This is because the prematurity problem limits the performance of GA.

As discussed above, the performance of an algorithm can be improved if more CPU time is given. For instance, DP can find a better solution if we use a smaller increment while GA can improve its solution quality as well if a larger population size is used. For the conditions and parameters discussed here, it is clear that both DP and GA can perform well in either CPU time or solution quality. There then exists a tradeoff between CPU time and solution quality, which helps to identify how much computation is necessary to improve the solution quality. Therefore, we conducted a perturbation analysis to obtain the tradeoff by varying the major parameters of GA and DP. The relationships between the power release and CPU time for different numbers of units are shown in Fig. 4.

Fig. 4 Power release vs. CPU time for different numbers of units

Note that we fit the scatters in Fig. 4 with exponential curves. Fig. 4 shows that the solution quality can be improved for both algorithms with the increase of CPU time, but the improvement decreases gradually. This rule demonstrates that it is not worthwhile to pursue a minor improvement at the expense of consuming a large amount of CPU time.

GA has an advantage over DP in finding better solutions for solving low-dimensional problems when the CPU time is very limited. For instance, for solving an ELD problem for a 16-unit system, GA is not as efficient as DP. This is because GA is a heuristic search method; it will lose its efficiency when finding a global optimum in a large solution space. Also, GA’sdeficiency in performing local searches limits its performance in refining solution quality. In contrast, DP searches the solution space thoroughly by enumerating the discretized grids. Although it costs significant CPU time, the solution quality can be guaranteed.

6 Conclusions

In this study, we conducted numerical experiments to compare the efficiency of DP and GA in hydro unit economic load dispatch. The experiments were applied to the Three Gorges Reservoir, which has 26 hydro units. Specifically, we introduced the performance metrics and designed two experimental schemes for conducting a performance comparison. The results of the experiments show the following:

(1) The performances of the two algorithms are strongly affected by their parameters as well as their applications. GA is adept at searching for optimal solutions in low-dimensional cases. In some cases, such as with a number of units of less than 10, the performance of GA is superior to that of DP. However, as a heuristic search method, GA loses its superiority in high-dimensional cases.

(2) DP has a good performance in obtaining stable and high-quality solutions, even in searching through large solution space. However, due to its exhaustive enumerating nature, it costs excess time in low-dimensional cases.

Bahmanifirouzi, B., Farjah, E., and Niknam, T. 2012. Multi-objective stochastic dynamic economic emission dispatch enhancement by fuzzy adaptive modified theta particle swarm optimization. Journal of Renewable and Sustainable Energy, 4(2), 0231052. [doi:10.1063/1.3690959]

Bakirtzis, A., Petridis, V., and Kazarlis, S. 1994. Genetic algorithm solution to the economic dispatch problem. IEE Proceedings: Generation, Transmission and Distribution, 141(4), 377-382.

Baskar, S., Subbaraj, P., and Rao, M. V. C. 2003. Hybrid real coded genetic algorithm solution to economic dispatch problem. Computers and Electrical Engineering, 29(3), 407-419. [doi:10.1016/S0045-7906(01)00039-8]

Benhamida, F., and Abdelbar, B. 2010. Enhanced Lagrangian relaxation solution to the generation scheduling problem. International Journal of Electrical Power and Energy Systems, 32(10), 1099-1105. [doi:10.1016/j.ijepes.2010.06.007]

Cheng, C. T., Liao, S. L., Tang, Z. T., and Zhao, M. Y. 2009. Comparison of particle swarm optimization and dynamic programming for large scale hydro unit load dispatch. Energy Conversion and Management, 50(12), 3007-3014. [doi:10.1016/j.enconman.2009.07.020]

Chiang, C. L. 2007. Genetic-based algorithm for power economic load dispatch. IET Generation, Transmission and Distribution, 1(2), 261-269. [doi:10.1049/iet-gtd:20060130]

Coelho, L. D. S., and Mariani, V. C. 2009. An improved harmony search algorithm for power economic load dispatch. Energy Conversion and Management, 50(10), 2522-2526. [doi:10.1016/j.enconman. 2009.05.034]

Hemamalini, S., and Simon, S. P. 2011. Dynamic economic dispatch using artificial bee colony algorithm for units with valve-point effect. European Transactions on Electrical Power, 21(1), 70-81. [doi:10.1002/etep.413]

Holland, J. H. 1975. Adaptation in Nature and Artificial System. The University of Michigan Press: Ann Arbor.

Howard, R. A. 1960. Dynamic Programming and Markov Process. Cambridge: Technology Press of Massachusetts Institute of Technology and John Wiley and Sons, Inc.

Hrstka, O., and Kucerova, A. 2004. Improvements of real coded genetic algorithms based on differential operators preventing premature convergence. Advances in Engineering Software, 35(3-4), 237-246. [doi: 10.1016/S0965-9978(03)00113-3]

Kumar, S., and Naresh, R. 2009. Nonconvex economic load dispatch using an efficient real-coded genetic algorithm. Applied Soft Computing, 9(1), 321-329. [doi:10.1016/j.asoc.2008.04.009]

Li, F., Morgan, R., and Williams, D. 1997. Hybrid genetic approaches to ramping rate constrained dynamic economic dispatch. Electric Power Systems Research, 43(2), 97-103. [doi:10.1016/S0378-7796 (97)01165-6]

Liang, Z. X., and Glover, J. D. 1992. A zoom feature for a dynamic programming solution to economic dispatch including transmission losses. IEEE Transactions on Power Systems, 7(2), 544 - 550. [doi: 10.1109/59.141757]

Michalewicz, Z., Janikow, C. Z. 1996. GENOCOP: A genetic algorithm for numerical optimization problem with linear constraints. Communications of the ACM, 39(12), 175-201. [doi:10.1145/272682.272711] Ngundam, J. M., Kenfack, F., and Tatietse, T. T. 2000. Optimal scheduling of large-scale hydrothermal power systems using the Lagrangian relaxation technique. International Journal of Electrical Power and Energy Systems, 22(4), 237-245. [doi:10.1016/S0142-0615(99)00054-X]

Ongsakul, W., and Petcharaks, N. 2004. Unit commitment by enhanced adaptive Lagrangian relaxation. IEEE Transactions on Power Systems, 19(1), 620-628. [doi:10.1109/TPWRS.2003.820707]

Ongsakul, W., and Ruangpayoongsak, N. 2001. Constrained dynamic economic dispatch by simulated annealing/genetic algorithms. Proceedings of the 22nd IEEE Power Engineering Society International Conference on Power Electric Energy, 207-212. [doi:10.1109/PICA.2001.932349]

Orero, S. O., and Irving, M. R. 1996. Economic dispatch of generators with prohibited operating zones: A genetic algorithm approach. IEE Proceedings: Generation, Transmission and Distribution, 143(6), 529-534. [doi:10.1049/ip-gtd:19960626]

Panigrahi, B. K., Pandi, V. R., and Das, S. 2008. Adaptive particle swarm optimization approach for static and dynamic economic load dispatch. Energy Conversion and Management, 49(6), 1407-1415. [doi:10.1016/ j.enconman.2007.12.023]

Sinha, N., Chakrabarti, R., and Chattopadhyay, P. K. 2003. Evolutionary programming techniques for economic load dispatch. IEEE Transactions on Evolutionary Computation, 7(1), 83-94. [doi:10.1109/ TEVC.2002.806788]

Somasundaram, P., Kuppusamy, K., and Kumudini Devi, R. 2006. Fast computation evolutionary programming algorithm for the economic dispatch problem. European Transactions on Electrical Power, 16(1), 35-47. [doi:10.1002/etep.63]

Yamin, H. Y. 2004. Review on methods of generation scheduling in electric power systems. Electric Power Systems Research, 69(2-3), 227-248. [doi:10.1016/j.epsr.2003.10.002]

Yang, K. 1995. Multiple dynamic model used in economic operation of large hydroelectric station. Journal of Hohai University, 23(4), 85-90. [doi:10.3321/j.issn:1000-1980.1995.04.014 ] (in Chinese)

Zheng, J., Yang, K., and Lu, X. Y. 2013. Limited adaptive genetic algorithm for inner-plant economical operation of hydropower station. Hydrology Research, 44(4), 583-599. [doi:10.2166/nh.2012.198]

Zhong, P. A., and Tang, L. 2010. Sensitive analysis on the parameters of genetic algorithm applied in optimal operation of reservoir. Water Power, 36(11), 13-16. (in Chinese)

(Edited by Yan LEI)

This work was supported by the National Basic Research Program of China (973 Program, Grant No. 2013CB036406), the National Natural Science Foundation of China (Grant No. 51179044), and the Research Innovation Program for College Graduates in Jiangsu Province of China (Grant No. CXZZ12-0242).

*Corresponding author (e-mail: pazhong@hhu.edu.cn)

Received Mar. 5, 2013; accepted May 10, 2014