一类在幼年时期传播的SIS传染病模型分析

苏丹丹

（罗定职业技术学院教育系, 广东 罗定 527200）

一类在幼年时期传播的SIS传染病模型分析

苏丹丹

（罗定职业技术学院教育系, 广东 罗定 527200）

利用微分方程的稳定性理论与传染病模型的理论知识,研究了一类仅在幼年时期传播的SIS传染病模型,讨论了系统在平衡点处的稳定性态.并通过构造Liapunov函数, 得到了系统在无病平衡点与地方病平衡点处全局渐近稳定的阈值.

传染病模型; 平衡点; 局部渐近稳定; 全局渐近稳定

1 引言

近年来, 流行病模型的研究越来越受到重视.目前已有大量的文献研究传染病模型[1-3],然而大多数的文献都是假设传染病对所有人都具有相同的传染性.而事实上并非如此,有些传染病只在不同年龄阶段的人群中进行传播.如麻疹、水痘、幼儿急诊等传染病多发于幼年(儿童)阶段;而伤寒、副伤寒、血吸虫病、钩端螺旋体病、白喉、流行性脑脊髓炎等则多在成年人之间传染流行.因此考虑具有不同传染率的不同年龄阶段结构的传染病模型更具有其必要性和实际意义.

文献[4]讨论了具有幼年和成年两个阶段结构的SI传染病模型;文献[5-6]讨论了具有阶段结构的SIS传染病模型;文献[7]讨论了一类具有阶段结构和非线性接触率的SI传染病模型的渐近性态,但这些文献主要研究的是仅在成年个体中传播的传染病模型,而对仅在幼年时期传播的传染病模型的研究鲜见.因此，本文着重讨论了一类仅在幼年时期传播的SIS传染病模型.并结合文献[6,8,9,10]的理论方法得到了系统在平衡点处全局渐近稳定的阈值.

2 引理

引理 1［8］考虑一阶常系数线性微分方程组

的根(E为单位矩阵),li为零或正整数,由根λi的初级因子的次数决定.

若特征方程（2）的根均具有负实部,则方程组（1）的零解是渐近稳定的. 若特征方程（2）具有正实部的根, 则方程组（1）的零解是不稳定的. 若特征方程（2）没有正实部的根,但有零根或具零实部的根,则方程组（1）的零解可能是稳定的也可能是不稳定的,这要看零根或具零实部的根其初级因子的次数是否等于1而定.

引理 2［8］设给定常系数的n次代数方程

其中ai=0(对一切i>n ),那么方程（3）的一切根均有负实数部分的充要条件是下列不等式同时成立:

引理 3［8］假设微分方程组

3 模型建立

将所考虑的人群按年龄结构分为幼年和成年两个阶段,而传染病仅发生在幼年阶段,故将幼年人群分为易感人群和染病人群两类,假设该传染病不具有免疫性,即感染病人治愈后仍可再次受到感染.为此我们建立以下数学模型:

初始条件:

其中,S1（t）,S2（t）,I （t）分别表示t时刻幼年易感人群、成年人群和幼年染病人群的密度,α为出生率,r为幼年死亡率,β为成年死亡率,Ω为幼年转化为成年的转化率,b为因病死亡率,a为疾病传染率,c为治愈率,此外假设所有参数皆为正数.

定理 1是系统（5）的正不变集.

证 明对任意的（S1,S2,I）∈R+3,由（5）式可知

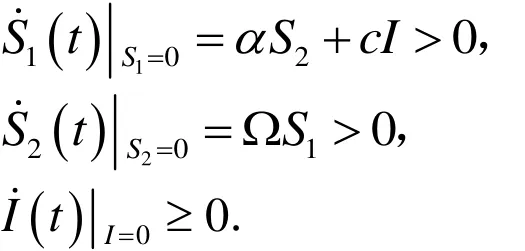
从而结论成立.

4 平衡态的稳定性分析

[1] YANNI XIAO,LANSUN CHEN. Analysis of a three species eco-epidemiological model[J]. J Math Anal Appl,2001, 258(2): 733-754.

[2] HETHCOTE H W,VAN-DEN-DRIESSCHE P. Two SIS epidemiologic models with delays[J]. Math Biol, 2000, 40(1): 3-26.

[3] MICHAEL Y LI,MULDOWNEY J S. Global stability for the SEIR model in epidemiology[J]. Math Bilsci ,1995, 125(2): 155-164.

[4] 原存德, 胡宝安. 具有阶段结构的SI传染病模型[J]. 应用数学学报,2002, 25(2): 193-203.

[5] 胡宝安, 陈博文, 原存德. 具有阶段结构的SIS传染病模型[J]. 生物数学学报, 2005, 20(1): 58-64.

[6] 张双德, 郝海, 李宏伟. 一类具有两阶段结构的自治SIS传染病系统[J]. 大学数学, 2004, 20(1): 7-11.

[7] 邱志鹏, 王开发. 具有阶段结构和非线性接触率的SI传染病模型的渐近性态[J]. 生物数学学报, 2004, 19(2): 156-160.

[8] 王高雄, 周之铭, 朱思铭, 王寿松. 常微分方程[M]. 北京:高等教育出版社, 2003: 240-302.

[9] 马知恩, 周义仓.常微分方程定性与稳定性方法[M]. 北京:科学出版社, 2001: 41-96, 296-300.

[10] 马知恩. 种群生态学的数学建模与研究[M]. 合肥: 安徽教育出版社, 1996: 51-55.

Analysis of a kind of SIS epidemic model disseminated in childhood

SHU Dan-dan
(Department of Education, Luoding Polytechnic College, Luoding 527200, P.R.C.)

The stability and the epidemic model theory of the differential equation are used in this paper, and a kind of SIS epidemic model only disseminated in childhood is studied. The stable condition of system in equilibrium point is discussed. In addition, by constructing Liapunov function, the global asymptotic thresholds of disease free and the endemic equilibrium are obtained.

epidemic model; equilibrium point; local asymptotic stability; global asymptotic stability

O175

A

1003-4271(2014)02-0249-07

10.3969/j.issn.1003-4271.2014.02.16

2013-12-06

苏丹丹(1980-), 女, 湖北随州人, 讲师, 硕士; 研究方向: 应用数学.(E-mail:sudandan@163.com)

国家自然科学基金重大项目(10990011).