波浪在不平坦海岸底床上传播的平面二维数学模型
2014-03-15彭延建刘应中时钟
彭延建,刘应中,时钟
(上海交通大学 船舶海洋与建筑工程学院 港口与海岸工程系,海洋工程国家重点实验室,上海 200030)
波浪在不平坦海岸底床上传播的平面二维数学模型
彭延建,刘应中,时钟*
(上海交通大学 船舶海洋与建筑工程学院 港口与海岸工程系,海洋工程国家重点实验室,上海 200030)
基 于线性波 浪 理论,利用摄动 理 论 中 的 多 重 尺度 法 , 以坡度 ε 为小 参 数 , Liu 和 Shi[1]推导出 波 浪 在不 平 坦底床传播的波幅方程,以及一阶势函数的解析解。为验证该模型是否可用于平面二维波浪传播问题,利用有限差分法,分别对波幅方程和边界条件进行离散和求解,得到因折射、绕射引起的波幅和波向的变化。通过引入绕射因子,使该 模型的应用范围更为广泛,并且计算精度得到提高。将计算得到 的波向和波 高与 Berkhoff[2]、Berkhoff 等[3]椭圆形浅滩试验值进行比较,表明该模型可以应用于平面二维问题。
多重尺度法;波浪传播;不平坦底床
0 引言
波浪在不平坦海岸底床上的传播是波浪研究的重要课题之一。波浪在从深水区向近岸传播过程中,因为海岸地形变化等诸多因素,会发生浅化、折射与绕射等现象,波况也随之变化,比如:波长变短、波速变慢、波高先减小后增大、波向也会趋于与岸线垂直。本文拟对线性波浪在不平坦海岸底床上的传播进行初步研究,对海岸工程学科具有科学意义。
对波浪在不平底床传播问题的研究[4-9],大体有两种研究方法:
第一种是基于缓坡方程和 Boussinesq 方程等已经较为成熟的模型,寻求数学模型和数值求解方法的改进,比如在缓坡方程中引入底摩擦、波浪破碎、非线性、波流相互作用等效应,以及对缓坡方程的简化和近似,例如双曲形缓坡方程、抛物形缓坡方程等,国内外众多学者在这方面的努力使基于缓坡方程和 Boussinesq 方程的模型在计算精度、计算速度、稳定性等方面有了较大的提高,已经能够较为成功地应用于某些工程案例。这类模型也存在一些缺点,比如有的只适合大面积计算区域,有的只适合小面积计算区域,求解短周期波浪场需要较高的网格密度,需要较大的计算机内存,求解过程也较为耗时等。
第二种是理论解析的方法,例如通过直接求解底部边界条件、线性自由表面条件来推导波浪势函数的解,或通过摄动展开求波浪势函数的近似解。这类模型存在的问题是,给出的解析解形式一般是局限在某些特定条件下,例如二维的斜坡床底等特定水深地形。
根据以上论述,对波浪在不平底床传播问题的研究,多数研究还是基于缓坡方程和Boussinesq 方程,进行模型的改进和数值方法完善,而在进一步发展波浪在不平岸滩传播的数学模型方面的研究较少。所以,进一步发展波浪在不平底床传播的数学模型,对波浪在不平底床传播的研究是有意义的。
本文的目的为通过引入绕射因子,进一步扩展 Liu 和 Shi[1]提出的模型,并对其进行验证。
1 数学模型
本文采用的是 Liu 和 Shi[1]中的数学模型,为了全文的完整性,本章将数学模型的推导过程在此做简要介绍。本文数学模型的推导基于经典的线性波理论。以笛卡尔坐标系为参考坐标,水平x轴位于静水面,与岸线的交点为坐标原点,指向外海。z轴垂直于静水面,向上为正。静水水深为(x,y)的函数,即 h=h(x,y)。假设外海入射波为单色波,无穷远处水深不变,比如 z=-h0,h0是常数。其速度势函数如下:

式中:φ 为速度势;g为重力加速度;a0为深海波幅;i为虚数单位,ω 为波浪频率;k0为深海波数。
ζ为波面函数,代表自由水位高程,表达式为:

波浪的频率 ω 与波数 k0满足色散关系式:

波浪在向近岸传播过程中会因地形的变化发生变形效应,引起折射和绕射,如果地形变化剧烈还可能发生反射。
假设海底地形为缓变海底,(|▽h|/(kh))为一小量ε,即在一个波长范围内,h的变化很小。引入两种尺度,长尺度 (x˜,y˜)= ε (x,y) 和 短尺度(x,y),前者对应于地形变化的尺度,后者对应于波浪传播的尺度。利用多重尺度法,可以得到:
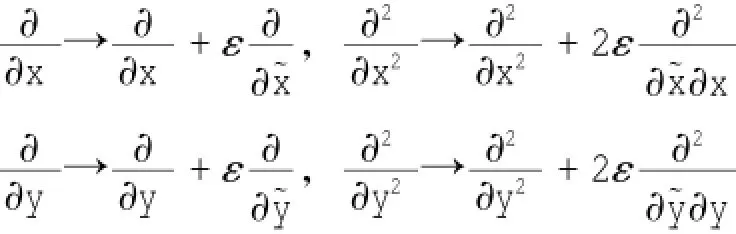
z方向只有一种尺度。假设解具有以下形式:

其中:φ0为零阶近似解;φ1为一阶近似解。将这些关系代入通常的线性波浪问题的控制方程和边界条件,可以得出:φ0满足拉普拉斯方程和自由表面边界条件及底部边界条件:

φ1满足:

无穷远处:

式 (6d) 说明,在无穷远处只存在零阶近似解。此处的一阶近似解是在线性波理论框架下考虑缓坡的高阶近似。
从式 (6a) ~ (6d) 可解得一阶近似解。对 x求偏导:

对 y,y˜的推导和 x,x˜类似。线性色散关系两边分别对 x˜和y˜求偏导,得到:
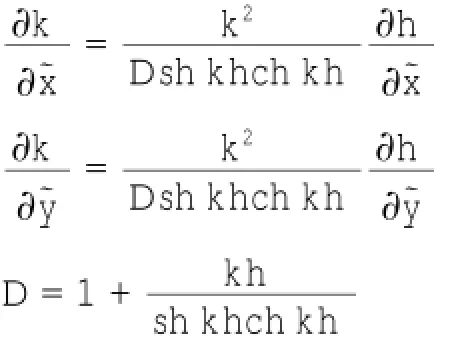
代入式(6a)~(6d),一阶近似解的方程和条件变为:
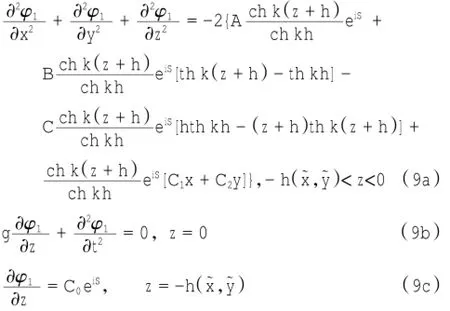
无穷远处,φ1=0。
其中:

以上推导中的参数均为关于水平尺度(x,y)的函数。假设一阶解的形式为:
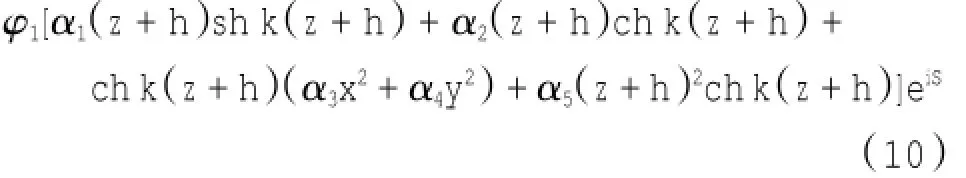
将式 (10) 代入式 (9a),比较等式两边的系数,得到:

需要指出的是,系数 αi,(i=1,2,3,4,5)均为实数,零阶近似解的波幅函数也在实数域内,所以一阶势函数 φ1= φa1meiS,幅值函数 φa1m也是实数。
结合色散关系式,将式 (10) 代入式 (9b),自由表面边界条件为:

将 αi(i=1,2,5)代入式 (12):

将 A ,C1,C2的表达式代入式 (13),得到波幅方程:

这里的波幅函数是零阶近似解的波幅。
2 计算方法
在每 个网 格点 ,k(x˜,y˜,t)与当地 深度 h(x˜,y˜,t)的关系是如同 h 为常数一样的色散关系。根据已知每个网格点的水深,及波浪在此传播过程中周期不变,可求得每个网格点的波数 k。波数无旋性条件还可写成如下形式:
式 (15) 为一阶的非线性偏微分方程,通过有限差分可以求得其数值解。
差分格式采用以下形式:
可用迭代法求解。w为权重因子,α为松弛因子,用以加速数值迭代之速度。当 w=1.0 时,方程为全隐格式。因为式 (16) 中,x 方向为向前差分,y方向为中心差分,引进权重因子 w,考虑第 i行 y方向中心差分的影响。松弛因子 α的作用是考虑 j-1 列和 j+1 列的影响。波浪传播方向的初值用 Snell定律求解,然后用迭代的方法求解式 (16),当两次求解的波向角相差小于某个小参数δ时,迭代停止。
下面为构造方程式 (14) 的 Crank-Nicolson[10]格式离散方程:
k1(i,j)代表 k1在 (i,j)处的值,k2(i,j)代表 k2在 (i,j)处的值。式 (17) 在波数 k 的离散和波幅的 y 方向做的 Crank-Nicolson[10]离散,x 方向是从外海边界到海岸方向做步进求解 (a0为波幅边界条件),计算格式实现了稳定,编程的工作量也相对减轻。
y方向透射边界条件:

3 计算实例
荷兰 Berkhoff[2]、Berkhoff等[3]的椭圆形浅滩试验是缓坡方程被引用最多的试验,试验地形和测量断面如图1所示。为了验证本文模型,根据上节中的方法,将本文模型应用于上述算例。采用等间距网格,Δx 和 Δy 均取为 0.25m。
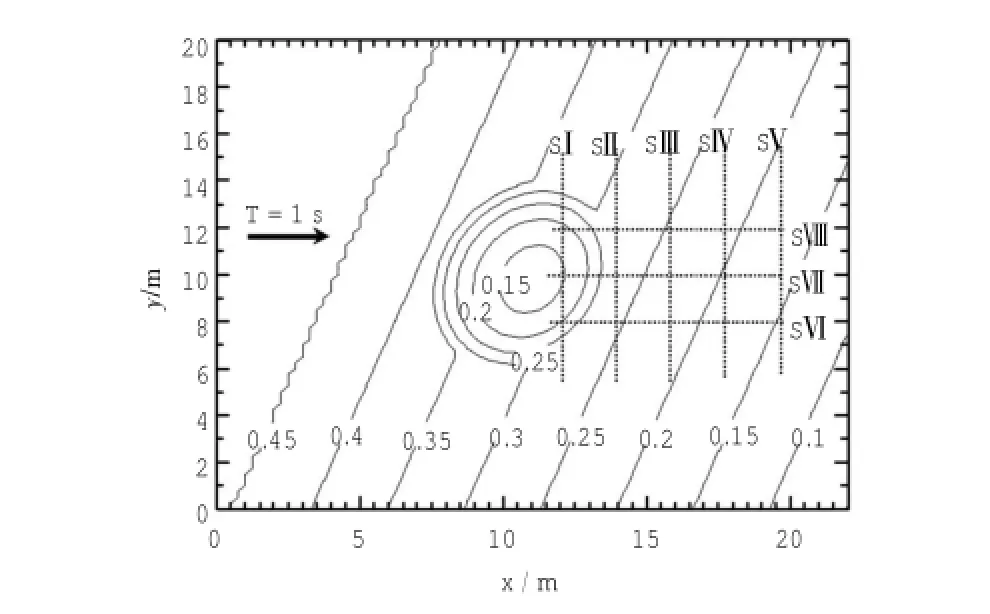
图1 Berkhoff[2]、Berkhoff 等[3]椭圆形浅滩试验水深等值线 (单位:m)及 8个波幅测量断面分布Fig.1 Contoursofwater depth(m)and distribution of eight sections for wave am p litudemeasurements of Berkhoff[2]、Berkhoff etal.[3]elliptic shoal test
根据上节中波浪传播方向的求解方法,计算得到的越过 Berkhoff[2]、Berkhoff等[3]试验椭圆形浅滩的波向角计算结果如图 2 所示。因为对 Berkhoff[2]、Berkhoff等[3]浅滩试验而言,波浪传播方向的变化主要发生在浅滩之后,浅滩之前和靠近侧边界的地方波向基本没有变化,所以,在图2中,只选取了部分区域,比如在图 2 (a) 中,取 5m 图2 本模型计算得到的波浪越过 Berkhoff[2]、Berkhoff等[3]试验中椭圆形浅滩的波向量分布Fig.2 Distributionsofwave vectorscalculated by the presentm odelover the elliptic shoalof Berkhoff[2]or Berkhoff etal.[3]’s test 因 为 波 浪 传 播 方 向 很 难 测 量 , Berkhoff[2]、Berkhoff 等[3]试验中 没有提供波向角的试验数据。本文模型计算得到的波向角结果,以及其他模型的波向角结果,均不能通过试验数据验证精确性。鉴于以上原因,本文通过与其他模型的波向角计算结果比较,分析计算结果的合理性。Maa 等[11]针对应用较为广泛的几种模型,如 REF/DIF-1、RCPWAVE 等,做了归类和比较,给出了各种不同模型关于波向角的计算结果。总结各个模型波向角计算结果的特点,波向的改变主要发生在浅滩后,并且向浅滩后的中心线相聚,这与本文的结果图 2 中 (b) 区域是符合的。 位于浅滩后的8个断面的计算值和试验值的对比如图 3。对于 Berkhoff[2]、Berkhoff等[3]的特定地形,本文计算值给出了一个较为合理的结果,波高分布与试验值较为相似。断面SⅠ的计算值与试验值非常吻合;断面SⅡ的计算值与试验值在浅滩两侧吻合的较好,在浅滩上计算值要高于试验值;断面 SⅢ、断面 SⅣ和断面 SⅤ位于浅滩后,由于折射作用,会发生波能的相聚,波高增大,某些区域达到了入射波高的两倍多,本文计算值给出了一个在波高和变化趋势上非常接近的结果,但是没有反映出两侧波高“减小—增大—减小”波动的过程。在向岸方向的3个断面中,断面SⅥ计算值与试验值吻合程度不够理想,断面 SⅦ和断面 SⅧ计算值与试验值吻合较好。 图3 本模型计算值与 Berkhoff[2]、Berkhoff 等[3]椭圆形浅滩试验 8 个断面(SⅠ、SⅡ、SⅢ、SⅣ、SⅤ、SⅥ、SⅦ和 SⅧ) 的相对波高试验值比较Fig.3 Com parison between calculated relativewave heightsby the presentmodeland experimental data for eight sections(SⅠ,SⅡ,SⅢ,SⅣ,SⅤ,SⅥ,SⅦ,and SⅧ) of Berkhoff[2]、Berkhoff etal.[3]'selliptic shoal test 本文数值结果的不足及其原因: 1) 如图 3 所示,在刚过浅滩的地方,断面SⅡ与断面 SⅢ之间,计算值略高于试验值,这可能是由于本文模型为线性模型,没有考虑非线性作用。如果考虑非线性作用,能够得到更好的结果。在本模型以后的研究中,可以引入非线性色散关系来考虑非线性效应。 2)与试验数据相比,在浅滩的后面,即入射边界 10m 之后,断面 SⅣ和断面 SⅤ缺少因绕射而引起的波高在浅滩两侧的波动,显得平滑。原因是因为引入了光程函数方程。 本文的目的是对 Liu 和 Shi[1]提出的 数学模式进行数值计算验证和扩展,使其可以应用于平面二维波浪变形问题,本文重点在于验证 Liu 和Shi[1]模型应用与平面二维问题的有效性。模拟的波高结果在部分断面上的计算精度尚需提高,今后,可以将计算结果与其它模型进行定量对比。 本文基于 Liu 和 Shi[1]的数学模型,引入绕射因子,利用有限差分法,对数学模型的波幅方程和边界条件进行数值离散,空间步进求解波浪由外海向近岸传播时,因为折射、绕射和浅化等波浪变形现象,引起的波高、波向等波浪要素的变化。将本文的数值模 型应用于经典的 Berkhoff[2]、Berkhoff等[3]椭圆形浅滩算例,并与其试验结果做比较验证,证实本文模型求解二维地形下的波浪折射、绕射是可行的,具有方程求解简单、可适用于大面积海域的优点。并且,光程函数的引入,使 Liu 和 Shi[1]的模型应用范围更广泛,在求解平面二维问题时精度得到提高。 [1]LIU Y Z,SHIJZ.A theoretical formulation for wave propagations overuneven bottoms[J].Ocean Engineering,2008,35(3-4):426-432. [2]BERKHOFF J C W.Computation of combined refractiondiffraction[C]//Proceedingsof the 13th international conference on coastalengineering.Vancouver,ASCE,1972:471-490. [3]BERKHOFF J C W,BOOIJ N,RADDER A C.Verification of numerical wave propagation models for simple harmonic linear waterwaves[J].Coastal Engineering,1982(6):255-279. [4]ECKARTC.The propagation of gravitywaves from deep to shallow water[M]//Gravitywaves.Washington DC:National Bureau of StandardsCircular 521,1952:165-173. [5]BIESEL F.Study ofwave progression in waterofgradually varying depth[M]//Gravity waves.Washington D C:National Bureau of Standards Circular521,1952:243-253. [6]BATTJESJA.Refraction ofwaterwaves[J].Journalof theWaterways,Harbors and Coastal Engineering Division ASCE,1968,WW4:437-451. [7]MEIC C,LEMEHAUTE B.Note on the equations of long waves over an uneven bottom[J].Journal of Geophysical Research,1968,71:393-400. [8]MEIC C,TLAPA G A,EAGLESON PS.An asymptotic theory for water waves on beaches of mild slope[J].JournalofGeophysical Research,1968,73:4 555-4 560. [9]LIU P L F,DINGEMANS M W.Derivation of the third-order evolution equations for weakly nonlinear water waves propagating over uneven bottoms[J].WaveMotion,1989,11:41-64. [10]CRANK J,NICOLSON P.A practical method for numerical evaluation ofsolutions ofpartialdifferentialequationsof the heatconduction type[J].Proceedings of the Cambridge Philosophical Society,1947,43:50-67. [11]MAA JP Y,HSU TW,TSAIC H,JUANG W J.Comparison of wave refraction and diffractionmodels[J].Journal ofCoastal Research,2000,16:1 073-1 082. A two-dimensional horizontal numericalmodel of wave propagation over an uneven coastal bottom PENGYan-jian,LIUYing-zhong, SHIJohn Z. Based on the linearwave theory,by using themultiple-scalemethod and a small slope parameter ε,Liu and Shi[1]obtain the first-order approximate solutions of the wave potential function,aswell aswave amplitude equation, for the problem of wave propagation over an uneven coastal bottom.This study introduces the diffraction factor,which expands Liu and Shi[1]'s application range and improves itsaccuracy.Both wave amplitude equation and boundary conditions are discretized and solved by the finite differencemethod.Variations in wave amp litude and direction ofwave propagation caused by the refraction and diffraction are obtained.The validation study hasbeenmade useing of theexperimental results of Berkhoff[2]or Berkhoff et al[3]'selliptic shoal test.It is suggested that the presentmodelbe applied to two-dimensionalwave propagation problems. multiple-scalemethod;wave propagation;uneven bottom TV139.2 A 1003-3688(2014)01-0008-06 10.7640/zggw js201401002 2013-04-12 2013-09-02 海洋工程国家重点实验室自主研究课题 (GKZD010056-9) 彭延建 (1982 — ),男,山东德州市人,硕士,工程师,港口 海岸及近海工程专业。 * 通讯作者:时钟,E-mail:zshi@sjtu.edu.cn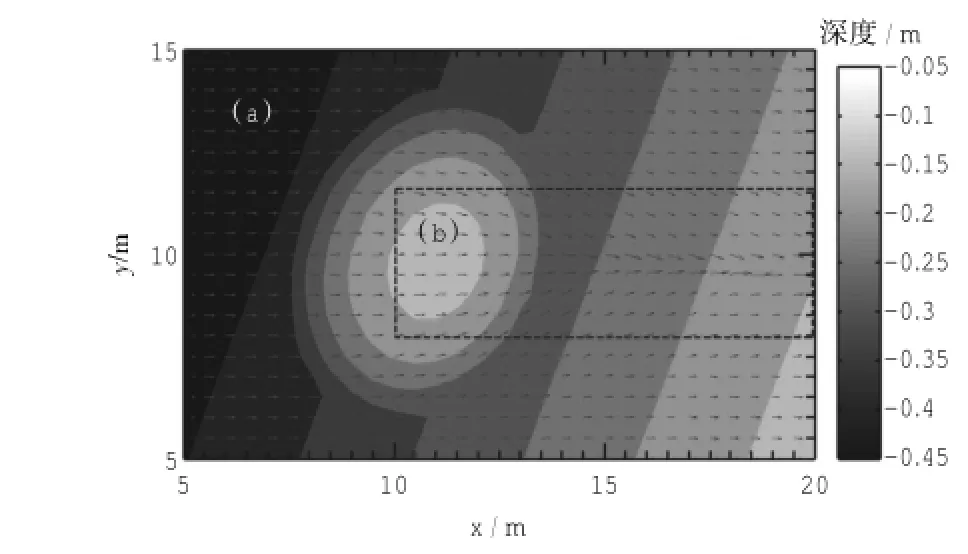

4 结语
(SchoolofNavalArchitecture,Ocean and CivilEngineering,Shanghai Jiao Tong University,Shanghai200030,China)
