基于细观力学精确建模方法的自适应底座力学性能研究①

仲健林，任 杰，马大为，聂 赟，胡建国

(1.南京理工大学 机械工程学院，南京 210094；2.北京机电工程总体设计部，北京 100854)

0 引言

自适应底座是实现筒装导弹冷弹射的关键部件，对其建立精确数值模型及其力学特性的研究能有效推动导弹冷发射技术的发展[1]。自适应底座由帘线/橡胶复合材料经多层粘接热压而成，复合材料数值模型建立方法的研究是建立自适应底座精确数值模型的前提。任旭春等[2]提出了帘线/橡胶复合材料的一种非线性数值模型，推导了该模型的有限元格式。郭国栋等[3]基于纤维增强复合材料连续介质力学理论，提出了帘线/橡胶复合材料的各项异性超弹性本构模型。刘文博等[4-5]基于复合材料细观力学采用有限元法计算了复合材料有效弹性模量。Abe A等[6-8]研究了帘线/橡胶复合材料的非线性、粘弹性等，模拟了帘线/橡胶复合材料的特性。由束纱拉伸实验可知，复合材料中帘线股数的不同会导致帘线拉伸模量的改变[9]。然而，目前涉及帘线/橡胶复合材料力学性能的数值研究中并未体现这一点；另外，目前针对自适应底座精确数值模型建立方法及其力学性能的研究也鲜见报道。

本文以自适应底座为研究对象，建立帘线/橡胶复合材料数值模型，结合自适应底座细观力学模型，建立自适应底座试验状态下数值模型，搭建试验平台测得附加载荷试验值，采用参数辨识法[10]，研究帘线组分参数对其附加载荷等力学性能的影响。研究结果能为自适应底座精确数值模型的建立提供参考，为自适应底座的结构设计与优化提供了理论依据。

1 复合材料数值模型与试验验证

自适应底座由多层帘线/橡胶复合材料单层板经粘接后在模具上热压成型，要较好地模拟自适应底座的力学性能，必须正确建立帘线/橡胶复合材料数值计算模型。帘线/橡胶复合材料为薄层结构，采用壳单元并赋予相应材料模型模拟橡胶基体，使用Rebar单元模拟帘线增强相。

1.1 橡胶材料Mooney-Rivilin模型及参数求解

在帘线/橡胶复合材料中，假设帘线与橡胶的连接界面不发生破坏，橡胶材料的变形程度受到帘线约束，属于中小变形范围，采用适用于中小变形的Mooney-Rivilin应变能密度函数对其进行描述，该模型为典型的二项三阶展开式：

(1)

式中C10、C01和D1为材料常数；I1和I2分别为变形张量的第一和第二不变量。

橡胶为不可压缩材料，J=1，则式(1)可简化为

(2)

橡胶材料的应力-应变关系可用应变能密度函数对其主伸长比求偏导表示，此应力-应变形式由Piola-Kirchhoff应力张量tij和Cauchy-Green应变张量γij之间的关系得到[11]：

(3)

由式(3)可得橡胶主应力ti与其主伸长比λi之间的关系：

(4)

对不可压缩材料和单向拉伸试验，设单轴拉伸方向伸长率为λ1，有以下关系[12]：

(5)

结合式(4)和式(5)推导出橡胶材料的主应力与主应变和变形张量不变量与主伸长比的关系：

(6)

(7)

(8)

式(8)即为拉伸试验中C10和C01关系式，可采用最小二乘法进行解算C10和C01的值。

图1 拉伸试验

自适应底座所用橡胶材料单向拉伸试验数据如图1所示，在试验曲线上取20组应力-应变值，结合式(8)采用最小二乘法解算得C10=0.774 9 MPa、C01=3.517×10-2MPa。将C10、C01值在有限元软件Abaqus中采用Mooney-Rivilin本构模型进行拟合，如图2所示。在100%应变内，拟合曲线和试验曲线符合较好，表明采用Mooney-Rivilin模型来表征橡胶材料发生中小变形时的本构关系是可行的。

图2 参数拟合曲线与试验曲线

1.2 帘线材料模量修正

在橡胶材料壳单元中，应用Rebar单元模拟帘线增强相[13]，如图3束纱拉伸模量实验曲线可知，纱线的平均拉伸模量值随纱线数量的增多而减小[9]。

图3 束纱拉伸模量实验曲线

针对图3，通过回归方法，取相关系数为0.999 8，得到回归方程[5]如式(9)所示：

En=E1n-0.052 9

(9)

式中n为束纱中纱线数量；E1为单纱拉伸模量；En为束纱的拉伸模量。

浸胶帘线中乳胶拉伸模量与纤维帘线的拉伸模量相差很大，由复合材料模量混合律可知，浸胶帘线的拉伸模量主要由纤维的拉伸模量与体积含量的乘积所决定，乳胶对浸胶帘线拉伸模量的贡献很小，可忽略乳胶的影响，认为浸胶帘线的拉伸模量也满足纤维帘线的变化规律，浸胶帘线的拉伸模量与帘线数量之间满足如下关系式：

E1n=E1nγ

(10)

式中n为浸胶帘线数量；Eln为帘线数量为n时的等效拉伸模量；γ为拉伸试验常数，与帘线本身材料特性有关。

1.3 单向拉伸试验验证

依据文献[9]中帘线/橡胶复合材料试件结构，建立其单向拉伸数值模型，求解等效弹性模量，与试验结果进行对比，验证橡胶材料Mooney-Rivilin模型参数求解和帘线模量修正公式的正确性。

图4为复合材料试件横截面示意图，试件尺寸长度l=100 mm，宽度b=25.4 mm，厚度h=6 mm，浸胶帘线直径d=0.75 mm，帘线角θ=0°，帘线在厚度方向均匀分布共分为5层，每层帘线数为19，帘线沿厚度和宽度方向的间距分别为δh=1.2 mm、δb=1.336 8 mm。

图4 试件横截面

采用1.1节中方法对文献[9]中橡胶的拉伸应力-应变曲线采样后求解得到Mooney-Rivilin模型参数C10=-0.273 MPa和C01=1.02 MPa，橡胶视为不可压缩材料，参数D=0。帘线与试件长度方向平行取θ=0°，试件厚度和宽度方向上的帘线间距δh和δb分别通过Rebar单元的间距和Rebar单元距壳单元中性面的距离设定，浸胶帘线拉伸模量为El=1 213.22 MPa，试件中含帘线数量n=95，拉伸试验常数γ=-0.052 9，将El、n和γ的值代入式(10)，求解帘线的修正拉伸模量为953.49 MPa。

复合材料等效拉伸模量的计算公式可表示为

(11)

式中Fi为第i次加载的载荷；Ei为复合材料试件的等效拉伸模量；ti为真实应力；ei为真实应变；λi为伸长率；Si为试件加载后的横截面面积；bi为试件加载后的宽度；hi为试件加载后的厚度。

橡胶为不可压缩材料，浸胶帘线由乳胶和纤维组成，乳胶为不可压缩材料，本文中纤维泊松比为0.43，可认为帘线/橡胶复合材料是近似不可压缩材料，假设拉伸过程截面变化均匀，采用加载前的截面尺寸和纵向拉伸率来表示式(11)，将其改写为

(12)

式中li为第i次加载后试件的长度；b、h分别为加载前试件的宽度和厚度。

通过数值模型仿真，得到帘线模量未修正和修正后复合材料伸长率随载荷变化曲线，如图5所示。

文献[9]中试件弹性模量实验值为257.79 MPa，将数值模型求得的伸长率代入式(10)进行计算，得到帘线模量未修正时帘线/橡胶复合材料等效弹性模量约为338 MPa，修正后约为266.6 MPa，与实物试件基本一致。可见，橡胶材料Mooney-Rivilin模型参数求解和帘线模量修正公式的正确性，可保证复合材料单层板数值模型的准确性。基于此，即可建立精确的自适应底座数值模型。

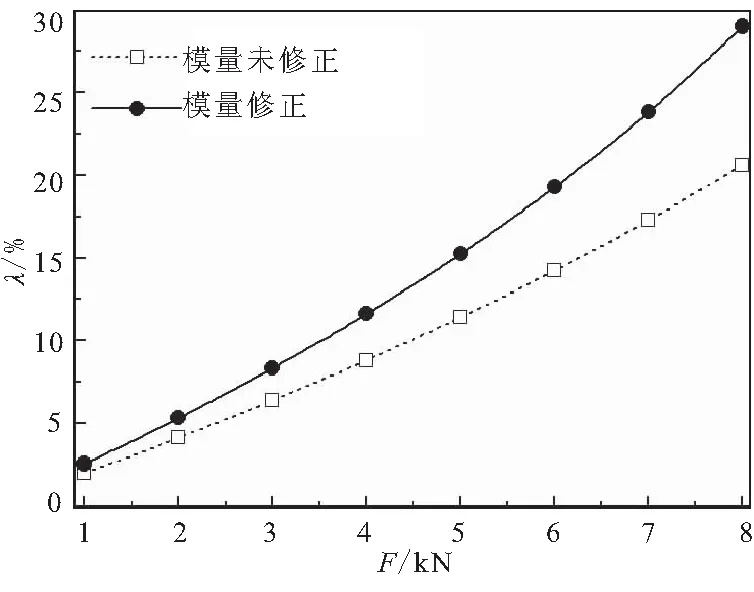
图5 伸长率变化曲线

2 自适应底座结构与细观力学模型

2.1 自适应底座结构

如图6所示，筒射导弹弹射系统主要包括导弹尾翼、弹射动力源、初容室、自适应底座。

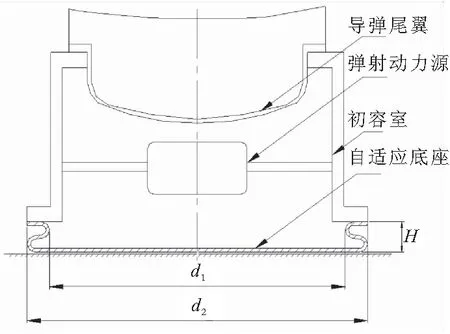
图6 导弹弹射系统

导弹弹射过程中，自适应底座在弹射气体作用下对初容室底部产生向下的拉力或向上的托力，称之为自适应底座的“附加载荷”。在初容室内高压气体作用下，自适应底座沿垂向和径向发生膨胀，与路面接触后能自动适应不同的路面状态，大幅降低弹射系统对发射场坪的要求。

自适应底座结构为轴对称结构，如图6所示，其主要特征是壁面表现为“S”形，称之为S弯。为方便描述，对涉及自适应底座几何尺寸的参数进行无量纲化处理，几何尺寸统一除以d2，壁面处最小直径为d1/d2=0.93，底座高度为H/d2=0.09。

2.2 自适应底座细观力学模型

如图7所示，某自适应底座的内、外层橡胶材料厚度均为0.5 mm，内部材料为15层帘线/橡胶复合材料层合板。如图8所示，帘线/橡胶复合材料的单层板也是轴对称结构，帘线的排列规则且分布均匀，帘线直径d=0.75 mm，复合材料单层板厚度h=1 mm，帘线间距δ=0.79 mm。

图7 底座层合示意图

图8 底座单层板截面图

底座复合材料单层板细观结构如图9所示，帘线按±45°方式对称铺层，图中有2个坐标系。其中，坐标系oxy是单层板的坐标系，另一坐标系是帘线的材料坐标系，1轴方向与帘线方向重合，帘线角θ为帘线1轴到复合材料y轴的夹角，规定逆时针为正方向。

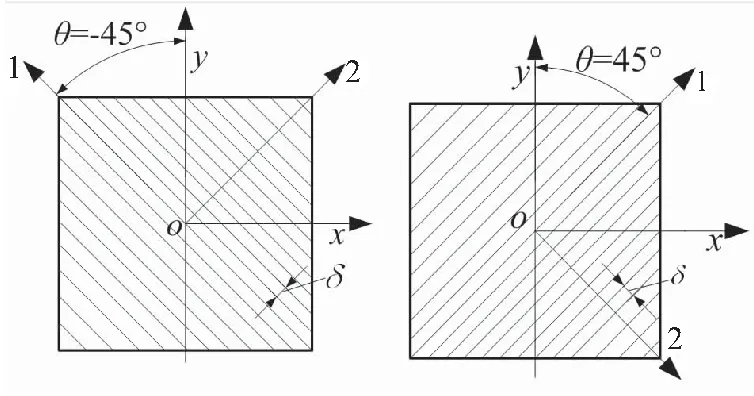
(a)45° (b)-45°

3 底座数值模型与试验验证

根据第2章中给出的自适应底座相关参数，建立试验状态下自适应底座数值模型，采用S4R单元对底座结构进行离散，Rebar单元模拟帘线增强相，通过Rebar单元的横截面面积来定义帘线的直径参数d，帘线角θ按所在层的具体位置取45°或-45°。在数值模型中定义自适应底座上端面和初容室底部固连，在初容室与自适应底座的连接界面上提取附加载荷作用力，按刚性地面建立数值模型，在自适应底座底面与地面之间建立接触关系，自适应底座数值模型如图10所示。试验中，采用夹板、密封圈以及多个螺栓将自适应底座的上端面固定在试验台安装台面上，在自适应底座内部进行加压，通过3个测力传感器来测量自适应底座产生的附加载荷，传感器分布点为测点1、测点2和测点3，如图11所示。

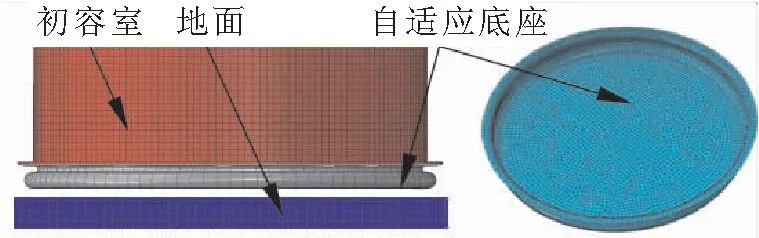
图10 自适应底座数值模型

图11 测力传感器分布

针对试验模型，将3个测点的附加载荷曲线叠加得到总附加载荷曲线。在数值模型中，提取自适应底座对初容室的作用力，即为附加载荷，对计算结果进行无量纲化处理。图12给出了无量纲化附加载荷随无量纲化时间变化曲线，数值模型解与试验测量值变化规律一致，附加载荷峰值的相对误差约为7%。可认为，所建数值模型能较好模拟自适应底座在较高压力作用下的工作特性，基于上述自适应底座数值模型，研究帘线组分对底座力学性能的影响是可行的。

图12 附加载荷对比

4 自适应底座力学特性影响分析

采用参数辨识方法[10]，基于既定结构的自适应底座，通过改变帘线模量和体积含量来研究帘线组分参数对底座的力学性能尤其是对附加载荷的影响规律，为底座的设计与优化提供理论依据。

4.1 工况规划

基于第3章中建立的底座数值模型，通过改变帘线的弹性模量和体积含量来获得相应的数值模型。由图8可知，复合材料单层板中帘线体积含量为h=πd2/4hδ，假设各工况中帘线直径不变，帘线间距δ由体积含量计算可得，数值模型中的帘线间距按其体积含量对应的值进行设定。模量E分别取60、40、20、10、5 GPa，对应于每种帘线模量，帘线体积含量η分别取50%、40%、20%和20%，共计20种工况进行数值分析，各工况对应的帘线弹性模量和体积含量如表1所示。

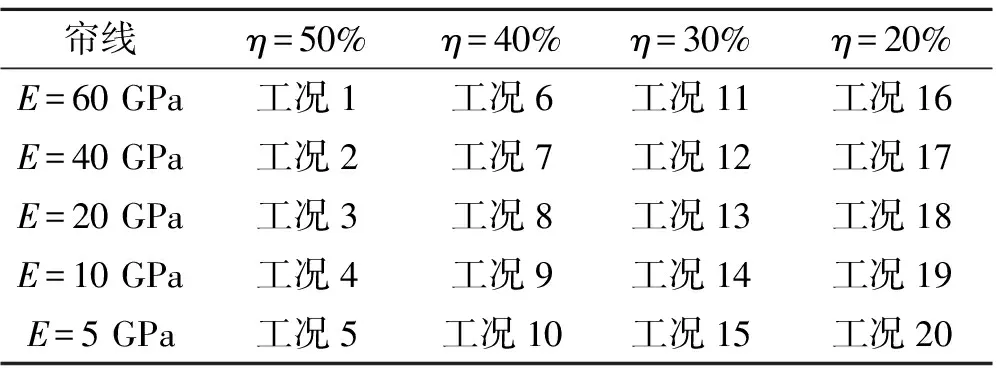
表1 帘线组分与对应工况

4.2 帘线组分对附加载荷的影响

分别对表1中的20种工况进行计算，得到了各工况对应的附加载荷曲线。限于篇幅，给出了帘线体积含量分别为40%、30%时自适应底座产生的无量纲化的附加载荷曲线，如图13所示。

各工况中附加载荷方向均向下，均在无量纲时间0.64左右达到最大值，取帘线模量E的值为x轴坐标，各工况附加载荷最大值为y轴坐标，绘制弹性模量与附加载荷关系曲线，如图14所示。

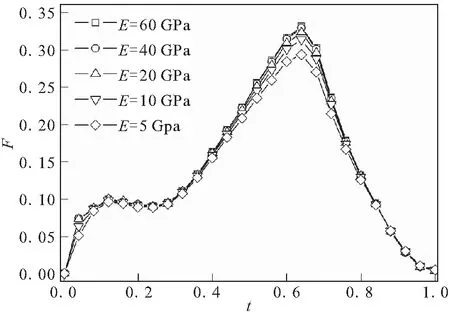
(a)η=40%

(b)η=30%

图14 帘线模量与附加载荷关系曲线

由图14可知，附加载荷不仅随帘线弹性模量的增大而增大，也随帘线体积含量的增大而增大。随着帘线弹性模量的增大，不同帘线体积含量对应的附加载荷有趋于相等的趋势。帘线弹性模量E相同时，附加载荷随帘线体积含量的增加而增加，帘线体积含量越大，附加载荷随帘线弹性模量增大的幅度就越小。帘线体积含量η相同时，附加载荷随帘线弹性模量的增大而增大，且增幅越来越小。

4.3 帘线组分对应力应变的影响

定义帘线层排列顺序为由自适应底座内部向外，第一层紧靠底座内壁面橡胶层，其余层依次向外排列，第8层为中间层，第15层与外壁面橡胶层相接。橡胶材料层从0层开始排列，0层和第16层分别为内、外壁面橡胶层，第1层至第15层与帘线层相对应。为分析帘线模量对底座应力应变的影响，取工况1和工况5的帘线和橡胶材料的最大主应力和最大主应变计算结果分析，为分析帘线体积含量对自适应底座应力应变的影响，取工况4和工况19的帘线和橡胶材料的最大主应力和最大主应变计算结果进行分析，提取以上4类工况0.64时第1层、第8层和第15层帘线/橡胶复合材料中橡胶与帘线的最大主应力和最大主应变，结果如表2所示。

表2 帘线体积含量与帘线间距对应表

由表2可知，4种工况橡胶材料的应力应变值不大，第8层帘线的应力应变值远小于第1层和第15层帘线的应力应变值，表明底座膨胀时，内外层受力状态比中间层更恶劣。帘线体积含量相同时，帘线弹性模量较高的工况，帘线的最大主应变值较小；帘线弹性模量相同时，体积含量较高的工况，帘线的最大主应力和主应变值较小。

4.4 帘线组分对剪应力与剪应变的影响

取体积分数为40%和30%的10个工况下单层板的剪应力和剪应变最大值进行分析，由于剪应力和剪应变有正值和负值，在此取绝对值较大的剪应力和剪应变，为直观体现各层复合材料单层板中最大剪应力、最大剪应变与所在层的关系，将最大剪应力、最大剪应变与所在层的对应关系分别绘制成曲线，如图15、图16所示。由图15和图16可知，复合材料层中剪应力和剪应变均表现为距中间层越远数值越大，最小值均在中间层附近出现。帘线体积含量相同时，帘线弹性模量越小，剪应力和剪应变值越大；帘线弹性模量相同时，帘线体积含量越低，剪应力和剪应变值越大。帘线弹性模量和帘线体积含量降低，会导致自适应底座的抗剪切能力下降。

(a)最大剪应力

(b)最大剪应变

(a)最大剪应力

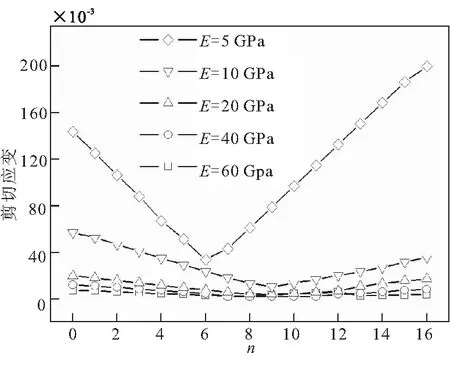
(b)最大剪应变

5 结论

(1)给出了橡胶材料Mooney-Rivilin模型参数求解方法，提出了帘线材料模量修正公式；建立了帘线/橡胶复合材料精确数值模型，仿真得到其等效拉伸模量与试验结果进行对比；数值模型所得到的等效模量和实物试件基本一致，文中给出的帘线/橡胶复合材料的精确建模方法正确，能为筒射导弹自适应底座的结构设计与优化提供技术支撑。

(2)基于自适应底座细观力学模型，建立了其试验状态下数值模型，通过数值计算和试验测得附加载荷对比验证，表明文中建立的数值模型能较好地模拟自适应底座的工作特性。

(3)采用高模量帘线时，自适应底座产生的附加载荷均很大，帘线体积含量的变化对附加载荷的影响较小。采用较低模量的帘线时，附加载荷最大值较小，帘线体积含量的变化对附加载荷的影响较大。如果仅从优化附加载荷的角度设计，采用较低的帘线体积含量，通过变化帘线弹性模量进行附加载荷优化的效果更好。

(4)自适应底座受压膨胀时，底座中橡胶材料的应力应变均不大，内外层受力状态比中间层更恶劣，提高帘线弹性模量或体积含量，均能降低帘线的应力和应变。

(5)距中间层越远剪应力和剪应变的数值越大，最小值均在中间层附近出现。帘线弹性模量和帘线体积含量降低，会导致自适应底座的抗剪切能力下降。

参考文献：

[1] Spearman M Leroy. Innovation in aerodynamic design features of soviet missiles[R].NASA 20080014230,2008.

[2] 任旭春,姚振汉.一种新的橡胶-帘线复合材料的模型及其参数识别方案[J].工程力学,2006,23(12):180-187.

[3] 郭国栋,彭雄奇,赵宁，等. 一种考虑剪切作用的各向异性超弹性本构模型[J].力学学报,2013,45(3):451-455.

[4] 刘文博,张洪涛,王荣国，等. 用有限元法对CF/ PPEK热塑性复合材料等效模量计算[J].哈尔滨工业大学学报,2006,38(4) 535-537.

[5] 焦亚男,李嘉禄,魏丽梅，等. 损伤形式对三维编织复合材料细观结构和弯曲性能的影响[J].固体火箭技术,2009,32(2):214-217,225.

[6] Abe A,Kamegava T,Kajima Y N. Optimum Young′s modulus distribution in tire design[J]. Tire Science and Technology,1996,24(3): 204-219.

[7] Padovan J.End effects in twisted cord-rubber composites[J].Tire Science and Technology,1996,24(4):321-338.

[8] Tret'yakova N A ,Khodakovo S Ya,Lyusova L R,et al.The creation of heat- and oil-resistant adhesive composites for rubber-cord products[J].International Polymer Science and Technology,2013,40(2):37-40.

[9] 高峰,姚穆.聚酰胺6帘线/天然橡胶复合材料中纤维体积含量对拉伸性能的影响[J].中国纺织大学学报,1996,22(3): 23-30.

[10] 刘君,夏智勋.动力学系统辨识与建模[M].长沙:国防科技大学出版社,2007

[11] Tian Z H ,Song H W ,Wan Z M ,et al .Fatigue properties of steel cord-rubber composite[J].Journal of Elasts & Plastics,2001,33(4):269-283.

[12] 任全彬,蔡体敏,安春利，等. 硅橡胶“O”形密封圈Mooney-Rivlin模型常数的确定[J]. 固体火箭技术,2006,29(2):130-134.

[13] 刘琥,倪晓琛,白静. 自适应底座悬垂弹射过程附加载荷分析[J].导弹与航天运载技术,2012(3)23-25.