基于DANS方程的粗糙床面明渠水力特性研究

李佳佳，李志伟，张长宽，陈永平，3

(1.河海大学港口海岸与近海工程学院，江苏南京 210098;2.香港理工大学土木及环境工程学系，香港; 3.河海大学水文水资源与水利工程科学国家重点实验室，江苏南京 210098)

在明渠湍流的研究中，人们通过具有光滑或粗糙床面的湍流模型来认识其流速、雷诺应力和紊动强度的垂线分布等复杂水力特性，这些水力特性对于明渠湍流的床面切应力、水流中泥沙起动和输移以及污染物质扩散等的研究都具有十分重要的意义。针对光滑床面明渠水流的模拟技术已较为成熟，但光滑床面是一种理想化的状态，在实际河道中，床面粗糙不平，复杂多变，因此研究粗糙床面明渠湍流水力特性更有助于认识天然河道的实际情况。

常见的计算流体力学模型多基于RANS方程(雷诺平均NS方程)，然而在实际水流中，尤其是近床区域，存在许多小尺度涡旋，使得时均流具有强烈的空间不均匀性，因而RANS方程并不适用。为了解决这一问题，有学者［1-4］提出一种基于DANS方程(双向平均NS方程)的模拟方法，先后在时间和空间上对NS方程进行平均，即在传统RANS方程的基础上再进行空间平均。该方法最初应用于气象研究［5］，后来逐渐被运用到水力学研究领域［1-4］。经过空间平均之后，DANS方程出现了一些新的物理项，如形状应力和形状阻力等。一般来讲，形状应力比雷诺应力小得多，在以往的研究中通常被忽略，但是近期的研究表明:形状应力并不是在任何情况下都可以被忽略的。Poggi等［6-7］用物理试验来研究植物分布密度对水力特性的影响，结果表明，当底部植物分布的密度很高时，形状应力可以被忽略;当底部植物分布得比较稀疏时，形状应力在植被以上的区域可以被忽略，而在植被分布层内的区域不能被忽略。Mclean等［8］用物理试验来模拟河床底部为沙丘时的明渠水力特性，给出了沙丘以上水域的试验数据，结果表明，在沙丘以上水域的形状应力可以忽略不计。Campbell等［9-10］用物理试验研究了砾石河床的相关状况，研究表明:形状应力在砾石顶部以上区域可以忽略，而在其以下区域则不能忽略，其贡献程度与雷诺应力相当。

从以上的研究成果可以看出，河床底部障碍物的材质及分布的疏密情况均会给明渠水力特性带来影响。Nikora等［3］研究发现，障碍物垂向分布的不均匀性也同样会给明渠的水力特性带来一定的影响，他将障碍物的垂向分布情况用孔隙率φ来表示，φ被定义为水的体积与总体积的比值，用以反映河床底部的地形分布状况。Nikora等［1-2］还系统地给出了考虑φ之后DANS方程推导的理论基础，并将其应用于明渠水流的模拟研究中。到目前为止，φ的相关研究成果并不多。

本文在前人研究的基础上，基于DANS方程建立粗糙面明渠水流数学模型，研究粗糙床面明渠水流的形状应力，定量探讨其存在对雷诺应力和速度分布的影响，并研究障碍物孔隙率的分布对形状应力、雷诺应力及垂线速度分布的影响。

1 数值模型的建立

为了简化模型，本文仅考虑均匀流的情形，DANS方程可以简化为一维的形式，忽略二次流影响后，其连续性方程和动量方程表述如下。

连续性方程:

动量方程:

S-A湍流模型是从经验和量纲分析出发［11］，由针对简单流动逐渐发展为适用于带有层流流动的固壁湍流流动的方程模型。

相对于两方程湍流模型，S-A湍流模型的计算量较小，稳定性好，计算网格在物面处不需要特别精细。在S-A湍流模型中，雷诺应力可表示为

于是式(2)变成:

式中:υt——湍流黏性系数，需要用S-A模型进行计算。

S-A湍流模型控制方程如下:

式中:L——流场中某点至壁面的最小距离;υ——S-A湍流模型中的黏性系数，通过S-A湍流模型控制方程给出;wz——旋转角速度。

与传统的RANS方程相比，DANS方程(式(2))多了新的一项该项的处理可以借鉴LES(大涡数值模拟)的思想［12-14］，即将形状应力视为LES内的亚格子应力项，采用与LES类似的亚格子涡黏模型来计算形状应力项:

式中:υs——亚格子涡黏系数;Cs——经验系数;Δ——网格空间步长。

将式(7)代入式(4)，DANS控制方程可改写为

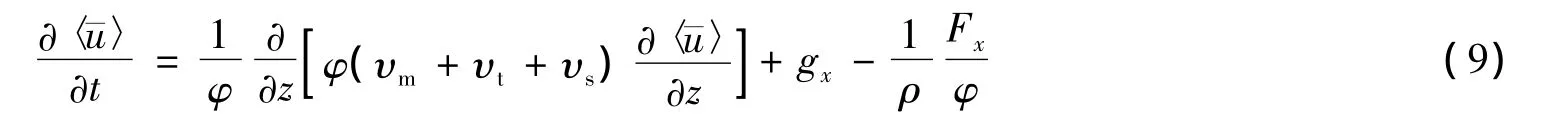
与传统的RANS方程相比，DANS方程还考虑了障碍物φ的影响［15］。对于障碍物以上的纯水区域，φ= 1;对于障碍物以下的区域，0≤φmin≤φ＜1。本文针对不同孔隙率分布状况对水流结构的影响进行研究对比。

2 形状应力对雷诺应力和垂向速度分布的影响

首先定量探讨形状应力的大小、分布及其对雷诺应力和速度分布的影响。计算值来源于本文建立的基于DANS方程的粗糙床面明渠水流数学模型模拟结果，用于验证的实测资料来源于Nikora等［3］的物理试验。该试验在一个长为12 m、宽为0.75 m的水槽内进行的，水槽底部被直径为63.9 mm的球体覆盖，采用声学多普勒流速仪(ADV)进行测量，分别测量了2种工况下的数据，见表1。表1中，Q为流量;H为水深;d0为障碍物高度;Re为雷诺数;u*为摩阻流速，反映壁面处阻力的大小，用于后续数据的无量纲化过程。

表1 文献［3］试验参数设置Table 1 Key parameters in experiment of literature［3］

图1分别为2种工况下粗糙床面明渠水流数学模型在Cs为0.05、0.10、0.15时形状应力、雷诺应力以及速度分布计算值，并与文献［3］的物理试验测量值进行对比验证。图中纵坐标由下至上代表从床底到水面的过程，0～1为障碍物分布层内，坐标1以上代表障碍物顶部以上至水面的水流区域。

从图1(a)(b)可看出，形状应力在障碍物分布层内是不可忽略的，而在障碍物上部则逐渐减小直至可忽略不计。由图1(c)(d)可见，Cs=0时，形状应力值为零，雷诺应力值最大。当z/d0=1时，即在障碍物顶部的位置时，雷诺应力达到最大值，并向水面线性减小，向底部也是逐渐减小的，计算结果与文献［3］的试验结果一致。雷诺应力由水面至障碍物顶部的线性增加是由重力分量的作用引起，而其从障碍物顶部至河床逐渐减小则是由于在障碍物层内存在拖曳力及形状应力与其共同保持与重力分量的平衡。图1(e)(f)为速度的垂向分布图，由计算值与实测值对比可知，在障碍物分布层以内，速度分布呈线性分布，而在其上部则符合对数分布规律。速度值随形状应力的增大而减小，这与理论预期是一致的，当水流中引入的阻力越大，水流速度就相应变得越小。

图1 不同Cs条件下形状应力、雷诺应力以及速度的垂向分布Fig.1 Vertical distributions form-induced stress，Reynolds stress，and velocity with different values of Cs

3 障碍物孔隙率对水流特性的影响

同样采用文献［3］的试验进行障碍物孔隙率分布的影响研究，孔隙率分布状况见图2。0.5常数分布是指在障碍物层内φ为常数0.5，在障碍物层以上即纯水区域为1;0.5线性分布是指在河床底部障碍物φ为0.5，并且在障碍物层从河床底部到障碍物顶部由0.5线性变化至1;同样，0.5分段分布指的是在河床底部至障碍物层一半高度处φ为0.5，并从障碍物一半高度处由0.5至1线性变化至障碍物顶部纯水区域;此外在研究过程中还取了1.0常数分布，指的是在计算域内忽略障碍物分布的影响。计算值与实测值的对比验证结果见图3。

图3为在不同的孔隙率分布状况下形状应力、雷诺应力以及速度的垂向分布图。从图3(a)(b)可以看出，不同的φ分布状况对形状应力分布有一定的影响，适当改变φ分布，计算值会更加接近实测值。从图3(c)(d)可以看出，当φ为0.5常数分布时，由于φ在障碍物顶端处存在突变，因而雷诺应力在此处也有一定的突变。从图3(e)(f)中看出，φ的分布对其速度分布影响并不大，并且φ分布越光滑对其影响越小。

图2 孔隙率φ的分布Fig.2 Distribution of porosity φ

图3 不同孔隙率分布条件下形状应力、雷诺应力以及速度的垂向分布Fig.3 Vertical distributions of form-induced stress，Reynolds stress，and velocity with different distributions of porosity

4 结 语

本文基于DANS方程，运用修正的S-A湍流模型，采用涡黏系数法建立了粗糙床面明渠水流数学模型，用该模型计算了速度、雷诺应力及形状应力的大小及分布并与实测值进行比较，此外还研究了底部障碍物的孔隙率分布情况对形状应力、雷诺应力以及垂线速度分布的影响，得到以下主要结论:

a.形状应力在障碍物分布层以内是不可忽略的，而在障碍物上部会迅速减小直至忽略不计。

b.形状应力的存在造成障碍物顶部附近的雷诺应力明显减小，但在障碍物顶部以上至水面区域，形状应力对雷诺应力的分布几乎无影响。

c.形状应力的存在使得速度有一定程度的减小，并且形状应力值越大，速度会随之变得越小。

d.障碍物孔隙率的分布对速度、雷诺应力及形状应力等会存在一定的影响，并且当孔隙率的分布越光滑时，其影响越小。

在实际情况中，由于地形分布十分复杂，孔隙率的分布只能用理想化模型代替，由于目前有关孔隙率分布的实测验证资料较少，在数学模型研究中采用哪一种分布状况更为合理还有待进一步研究。

［1］NIKORA V，MCEWAN I，MCLEAN S，et al.Double-averaging concept for rough-bed open-channel and overland flows: theoretical background［J］.ASCE，Journal of Hydraulic Engineering，2007，133(8):873-883.

［2］NIKORA V，MCLEAN S，COLEMAN S，et al.Double-averaging concept for rough-bed open-channel and overland flows: applications［J］.ASCE，Journal of Hydraulic Engineering，2007，133(8):884-895.

［3］NIKORA V，GORING D，MCEWAN I，et al.Spatially averaged open-channel flow over rough bed［J］.ASCE，Journal of Hydraulic Engineering，2001，127(2):123-133.

［4］SMITH J D，MCLEA S R.Spatially averaged flow over a wavy surface［J］.Journal of Geophysical Research，1977，82(12): 1735-1746.

［5］WILSON N R，SHAW R H.A higher order closure model for canopy flow［J］.Journal of Applied Meteorology and Climatology， 1977，16:1197-1205.

［6］POGGI D，KATUL G G，ALBERTSON J D.A note on the contribution of dispersive fluxes to momentum transfer within canopies［J］.Boundary-Layer Meteorology，2004，111:615-621.

［7］POGGI D，PORPORATO A，RIDOLFI L，et al.The effect of vegetation density on canopy sub-layer turbulence［J］.Boundary-Layer Meteorology，2004，111:565-587.

［8］MCLEAN S，NIKORA V.Characteristics of turbulent unidirectional flow over rough beds:double-averaging perspective with particular focus on sand dunes and gravel beds［J］.Water Resources Research，2006，42，W10409，DOI:10.1029/ 2005WR004708.

［9］CAMPBELL L，MCEWAN I，NIKORA V，et al.Bed load effects on hydrodynamics of rough bed open channel flows［J］.ASCE，Journal of Hydraulic Engineering，2005，131(7):576-585.

［10］ABERLE J.Spatially averaged near-bed flow field over rough armor layers［C］//ELSA C T，CARDOSO A H，LEAL J G，et al. Proceedings of the International Conference on Fluvial Hydraulics.Lisbon，Portugal:Taylor＆Francis，2006:153-162.

［11］SPALART P，ALLMARAS R.A one-equation turbulence model for aerodynamic flows［C］//IANNOTTA B.30th Aerospace Sciences Meeting and Exhibit.Reno，USA:AIAA，1992:439.

［12］ZENG C，LI C W.Modeling flows over gravel beds by a drag force method and a modified S-A turbulence closure［J］.Advances in Water Resources，2012，46:84-95.

［13］LI C W，YAN K.Numerical investigation of wave-current-vegetation interaction［J］.ASCE，Journal of Hydraulic Engineering，2007，133(7):794-803.

［14］LI C W，XIE J F.Numerical modeling of free surface flow over submerged and highly flexible vegetation［J］.Advances in Water Resources，2011，34:468-477.

［15］MANES C，POKRAJAC D，MCEWAN I，et al.Turbulence structure of open channel flows over permeable and impermeable beds: a comparative study［J］.Physics of Fluids，2009，21(12):5109.