一种基于合同理论的动态频谱分配模型

李方伟，吕 静，朱 江

(重庆邮电大学移动通信技术重庆市重点实验室，重庆400065)

当主用户与次用户共享频谱时，会在一定程度上造成主用户性能的下降，如何使主用户愿意与次用户共享频谱是需要解决的一个关键问题。这个问题不能单纯依靠FCC授权来解决，因为主用户可以通过一直发送垃圾信息保持信道状态忙来阻止次用户的接入［1］。在无线资源共享模型中，急需建立一些合理可行的方案，提出有效的激励机制，使主用户积极的与次用户共享频谱资源。

认知无线网络中，每个网络实体作为一个单独的智能个体独立选择自身策略，与微观经济学中的问题类似，基于微观经济学的无线资源分配机制［2-3］如:拍卖、定价、合同已经被关注，并被证明是解决无线资源分配问题的有效方法。

文献［4］建立了一个基于定价的动态频谱分配模型，该模型中频谱拥有者通过调整售出频谱的质量、价格来使利益最大化，模型侧重考虑频谱拥有者之间的竞争对价格、系统效益的影响。文献［5］建立了一个基于委托—代理合同的频谱共享模型，通过建立主次用户的合同契约关系，设计了一种激励机制，解决拍卖模型中频谱共享过程容易受主用户单方操控的问题。文献［6］建立了一个垄断市场模型，提出采用合同的方式动态分配频谱，考虑了资源的差异性，不同质量的频谱被赋予不同的价格。然而该模型中次用户的传输功率和价格全部由主用户设定，次用户完全处于被动地位。

本文提出了一种改进的基于合同的动态频谱分配方式，主次用户通过签订合同建立契约关系，达到频谱共享的合作目的。模型中，由次用户制定向主用户的付费规则，主用户决定共享资源的质量，经过交换信息双方决定是否签订合同。定义系统效用为次用户在空闲频谱上获得的信道容量的等价评估值与由于次用户的接入对主用户造成的性能下降的等价评估值之差。经仿真分析验证，本模型可以在节约资源的基础上，获得的社会效用接近其在理论上即在数学上可以达到的最大值，有效地提高了频谱资源的利用率，实际应用上具有可行性。

1 系统模型

本文考虑网络中有1个主用户和N个次用户的认知网络，其中每个次用户为1个传输接收对，次用户随机分布在网络小区内。如图1所示，为1个主用户和4个次用户的认知网络。

图1 1个主用户和4个次用户的认知网络

1.1 信道共享模型

主用户的频谱资源在某些时刻未被充分利用，即主用户在某些时刻有一些空闲频段。主用户将空闲频段划分为多个信道，设共有M个空闲信道，假设每个信道的带宽相等，1个信道同时只能被1个次用户使用，不同次用户间的干扰忽略不计［7］。若某个次用户成功接入主用户的某个信道，根据香农公式，次用户可以获得的最大信道容量为

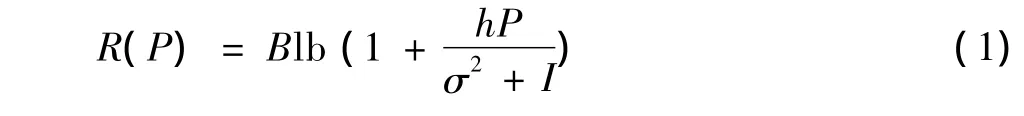
式中:B为信道带宽;P为次用户的发射功率;h为次用户的发射机到接收机的链路增益;I为主用户对次用户的干扰;σ2为信道上的其他噪声干扰。

1.2 基于合同机制的信道分配模型

为了激励主用户共享信道资源，次用户为自己获得的服务支付一定的费用以补偿激励主用户，参照经济学中的合同模型［8］，次用户的支付方式设计如下

式中:α是次用户使用主用户的信道需要支付的固定费用;β∈(0，1)是主用户分享的产出份额，即次用户获得的速率每提高一个单位，主用户的报酬增加β单位。

假设主用户在正常传输中专门划出特别时隙(或专门的认知导频信道)用于与次用户进行信息交互［9］。信道共享流程如下:

第一步:次用户有数据传输需要使用主用户的信道时，订立合同，说明其付费规则，将合同信息发送给主用户，提出使用信道申请。

第二步:主用户测量当前的信道环境，决定是否接受次用户的申请，若接受，则计算使自己效用最大时，允许次用户使用的最大发射功率，并将信息反馈次用户。

第三步:次用户计算在主用户给出的功率限制条件下，自己获得的效用，若效用为正则签订合同接入主用户的信道，否则放弃。

第四步:若主用户空闲信道全部分配完毕，则不再接收次用户的信道申请。

2 问题描述与分析

2.1 主用户分析

当次用户接入主用户的信道，会给主用户的通信增加干扰噪声，造成主用户一定程度上的性能下降，定义主用户与次用户共享信道资源的成本函数为［6］

式中:C0＞0代表主用户信道资源的固定成本花费，如购买信道资源授权许可证的花费等;aPb代表次用户的接入对主用户性能的影响，即主用户性能损失的等效评估值，如次用户的接入造成主用户系统噪声增大、信道容量减小等。a、b为成本系数，采用这种形式，体现了次用户功率越大造成主用户的性能下降越多，同时当次用户功率超过一定数值时主用户性能会急剧恶化这两个无线传输的特点。

定义主用户从每份合同中获得的收入为从次用户处获得的合同收入减去成本，由式(2)、(3)得知用户的效用函数为

主用户理性自私，其与次用户共享频谱资源的出发点为使空闲的频谱资源得到充分利用，进而获得额外的收入，其目标为最大化自身效用函数。主用户策略选择为决定允许哪个次用户接入其信道，以及次用户接入信道时的最大传输功率。

主用户目标为最大化自身效用函数，即

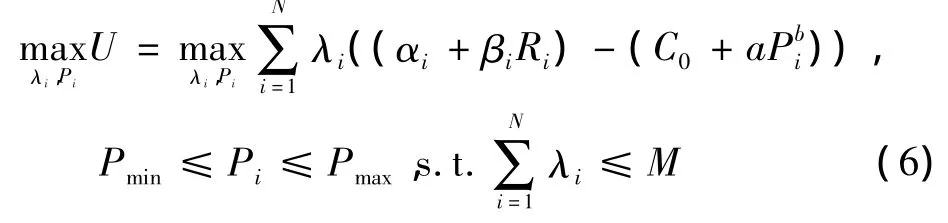
2.2 次用户模型

对于次用户i(i=1，2，…，N)，若其成功与主用户签订合同，由式(1)知，次用户i可以获得的信道容量为

定义次用户的收益为每单位的信道容量产生的等价的收入评估值［10］，即

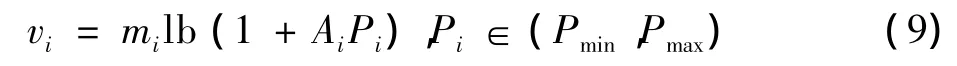
式中:mi＞0是相对于获得的每单位的信道容量的等价收益评估值，假设对于不同的次用户，这个评估值相同，下文统一用m表示。

次用户效用函数可表示为收入与成本的差值，根据式(2)、(8)和(9)，即

假设次用户为理性的，只有当使用主用户的信道后获得的效用为非负时，次用户才会使用主用户的信道。其中，当次用户效用为零时，虽然次用户未有正的收益，但是其业务得到正常进行，故此时次用户会接受合同。

由Vi≥0得:，即当次用户i允许使用的功率满足此条件时，次用户才会最终与主用户建立合同契约关系。次用户的策略可以描述为

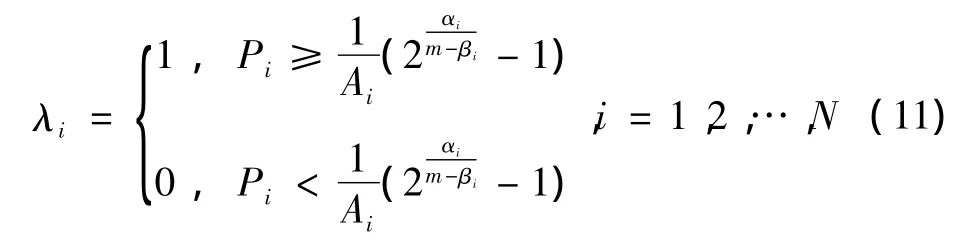
2.3 系统效用模型

次用户使用了主用户的空闲频谱资源，资源得到充分利用，提高了网络频谱利用率，增大了系统效益。定义增加的系统效用S表示为空闲信道得到使用后主、次用户产生的收益之和，由公式(5)、(10)得

增加的系统效用由两部分组成，一部分为次用户接入主用户信道业务得以进行获得的信道容量收入，另一部分为由于次用户的接入，主用户自身业务性能在一定程度上的下降，增加的系统效用即为这两部分的差值，这样定义的系统效用在一方面可以反应系统容量的大小。

分析可知，理论上系统效用最大的分配功率值为偏导数等于零的点。然而，在开放的市场中，主次用户是理性自私的，其目标为最大化自身效用而非最大化系统效用，实际情况中，主用户往往不会选择系统理论最佳功率。本文模型通过设计合理的合同机制，可以使最终系统效用较好的接近理论上的最优系统效用。

3 模型求解

由前所述，本文所提模型需要解决的问题为

模型的求解存在两种情况:

1)M≥N，即主用户信道资源足够，此时主用户可以接受所有次用户提出的信道请求，并根据每个次用户提出的合同设定允许其使用信道时的最大发射功率。2)M ＜N，即主用户信道资源有限，仅能满足部分次用户的需求，此时主用户选择接受使自己效用最大的前M个合同。则可以将问题进行简化，首先独立分析每个次用户合同下主用户的效用取值情况，然后根据信道资源充足与否情况分析主用户最终效用情况及次用户获得信道情况。则式(13)的求解可以等价变换为求解

在次用户i(i=1，2，…，N)提出的合同下，主用户获得的效用为

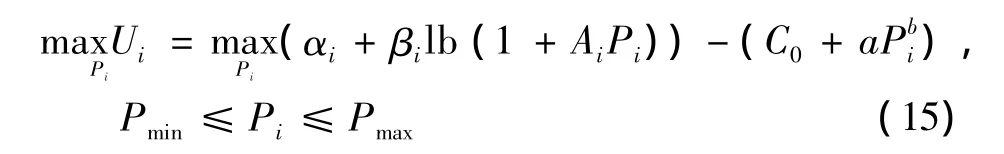
式(15)对功率求偏导数，可得

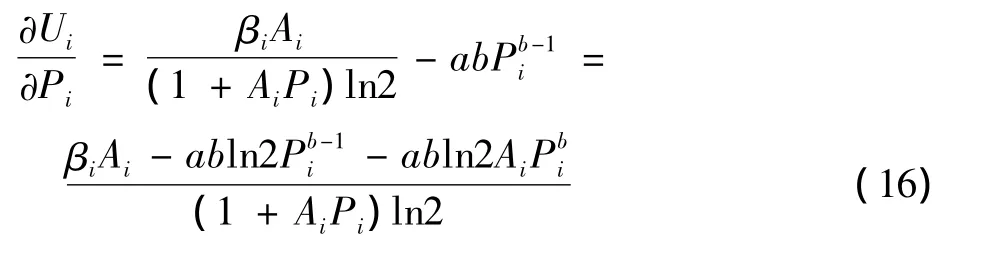
由于主用户的效用函数、效用函数对功率的偏导数均涉及到功率的小数次幂问题，采用传统的取偏导求极值的方法，很难求解，故本文引入粒子群优化算法求解主用户的策略选择问题。

粒子群优化算法［11］是根据鸟群觅食行为提出的一种基于群体智能理论的优化算法，算法采用速度-位置搜索模型，操作较简单，且具有一定记忆功能，是一种比较高效的并行搜索算法。采用粒子群算法，求解主用户的最优功率策略的算法具体流程为:

1)初始化主用户的功率策略，随机生成功率策略初始值:P=(p1，p2，…，pj，…，pJ)，更新速度初始值:Y=(y1，y2，…，yj，…，yJ)，其中 pj表示第 j个粒子的解空间的一个候选解，yj为第j个粒子的更新速度。

2)每次迭代速度和功率更新［12］为

式中:rand()为(0，1)区间的随机数，c1、c2为学习因子，一般取c1=c2=2。lj为每个粒子历史状态解中的最优功率解，g为所有粒子历史状态解中的最优功率解。

3)当达到最大迭代次数或满足最小错误标准时，算法结束，输出当前的最优功率解g，即为主用户的最优功率策略。

通过采用粒子群优化算法，可以较快、较好的找到不同次用户情况下主用户效用最大时的功率取值情况，得出主用户的功率选择策略，进而得出模型的解。

4 仿真分析

根据前面提出的网络模型，本文考虑主用户的空闲信道数M=15，有20个次用户(依次用1，2，…，20表示)的认知网络，其信道质量均匀分布在1～25之间，且随次用户编号的增大信道质量变好，假设每个次用户提出的合同相同，本文设计了三份不同的合同，仿真分析每份合同下各方面的性能。其他仿真参数设计如下:m=1.1，C=0.05，a=2，b=1.2。仿真中，粒子数取30个，迭代500次。仿真结果如图2～图5所示。

图2给出了不同情况下主用户的最终功率策略，即可以允许次用户所使用的最大传输功率，以及选择与其共享频谱的次用户。图3为对应情况下，主用户可获得的效用。图中，落在X轴上的点对应的次用户为未与主用户成功订立合同契约的次用户。由仿真图可以看出，合同系数相等的情况下，次用户信道质量越好，主用户可以允许其的传输功率越大，主用户从中获得的效用越大。因为主用户的资源限制，无法满足所有次用户的频谱申请，故主用户放弃信道质量最差的几个次用户的合同，优先与信道质量较好的次用户共享频谱资源。信道质量较差的次用户，若迫切需求频谱资源，则可以通过增大合同系数增加竞争力，进而获得频谱资源的使用权。

图2 允许次用户使用的功率

图3 主用户效用

图4 本文模型与理论值功率策略比较

图5 本文模型与理论值系统效用比较

图4、图5显示了当合同参数α=0.02，β=0.6时本文模型下策略与理论值的对比，其中图4为本模型下的功率策略与理论上功率分配方法的对比图，图5为本模型下获得的最终系统效用与理论上可获得的最大系统效用的对比。从仿真图可以看出，相比理论值，本文模型最大可节约功率41.59%，此时获得系统效用比理论值低6.04%，本模型有效地提高了频谱资源的利用率。

5 小结

本文建立了一个基于合同的频谱共享模型，主次用户通过订立合同契约达到共享资源的目的。合同的设计充分考虑次用户之间的差异性，并针对这些差异性设计不同的合同，以满足不同次用户的需求，从而达到资源的共享和合理利用。仿真分析表明，本模型在节约资源的同时，使获得的社会效用接近其在理论上的最大值，有效地提高了频谱资源的利用率，实际应用具有可行性。

［1］ATIA G，SAHAI A，SALIGRAMA V.Spectrum enforcement and liability assignment in cognitive radio systems［C］//Proc.DySpan Conference.［S.l.］:IEEE Press，2008:1-12.

［2］ZHU H，DUSIT N，WALID S，et al.Game theory in wireless and communication networks:theory，models，and applications［M］.New York:Cambridge University Press，2011.

［3］龙吟，朱江，李方伟.OFDM认知无线电系统中分布式资源分配［J］.电视技术，2013，37(1):118-121.

［4］JOYDEEP A，ROY D，YATE S.Service provider competition and pricing for dynamic spectrum allocation［C］//Proc.Game Theory for Networks，2009.［S.l.］:IEEE Press，2009:190-198.

［5］KALATHIL D，JAIN R.Spectrum sharing through contracts for cognitive radios［J］.IEEE Trans.Mobile Computing，2012(99):1-14.

［6］GAO Lin，WANG Xinbing，XU Youyun，et al.Spectrum trading in cognitive radio networks:a contract-theoretic modeling approach［J］.IEEE Journal on Selected Areas in Communications，2011，29(4):843-855.

［7］孙杰，郭伟，唐伟.认知无线多跳网中保证信干噪比的频谱分配算法［J］.通信学报，2011，32(11):111-117.

［8］张维迎.博弈论与信息经济学［M］.上海:三联出版社，1995.

［9］SUDHARMAN K，GONZALO V V，MOSQUERA C.Dynamic spectrum leasing:a new paradigm for spectrum sharing in cognitive radio networks［J］.IEEE Trans.Vehicular Technology，2010，59(5):2328-2339.

［10］JIANG Zhimei，GE Ye，LI Ye.Max-utility wireless resource management for best-effort traffic［J］.IEEE Trans.Wireless Communications，2005，4(1):100-111.

［11］JAMES K，RUSSELL E.Particle swarm optimization［C］//Proc.IEEE International Conference on Neutral Networks.［S.l.］:IEEE Press，1995:1942-1948.

［12］RUSSELL E，JAMES K.A new optimizer using particle swarm theory［C］//Proc.Sixth International Symposium on Micro Machine and Human Science.［S.l.］:IEEE Press，1995:39-43.