Detection of Supernova Neutrinos on the Earth for Large θ13∗

XU Jing(徐晶), HUANG Ming-Yang(黄明阳), HU Li-Jun(胡立军), GUO Xin-Heng(郭新恒),and YOUNG Bing-Lin(杨麟)

1College of Nuclear Science and Technology,Beijing Normal University,Beijing 100875,China

2Institute of High Energy Physics,Chinese Academy of Sciences,Beijing 100049,China

3Department of Physics and Astronomy,Iowa State University,Ames,Iowa 5001,USA

4Institute of Theoretical Physics,Chinese Academy of Sciences,Beijing 100190,China

1 Introduction

In the universe,core-collapse supernovas(SNs)are among the most energetic explosions.[1−3]They not only mark the catastrophic end of some stars,which turn into neutron stars or black holes after explosions,but also are responsible for the richness of heavy elements.[4−6]SN1987A has attracted worldwide interests and has been studied extensively since it came into our sight several decades ago.[7−8]During the explosions of the type II SN,most of the binding energy is released as neutrinos,which are very useful for acquiring information about the intrinsic properties and the explosion dynamics of SN.[3,7]

For the past few decades,in most theoretical models,it had been believed that the neutrino mixing angle θ13was smaller than 3°,or even smaller than 1.5°.In Refs.[9–10],the authors studied possible methods to measure this neutrino mixing angle while θ13＜ 3°.However,in recent years,some new experimental results indicated a large θ13(by large θ13we mean θ13≃ 9°).[11−16]Last year the Daya Bay experiment measured the value of θ13to 5.2σ accuracy and obtained the result θ13=8.8°± 0.8°,[15]which is much larger than 3°.Table 1 shows a summary of the recent experimental results about θ13.In this paper,we will study detection of SN neutrinos on the Earth in the case of large θ13.

SN neutrinos are produced from the core-collapse of SN and propagate outward to the surface of SN.Then they travel a long cosmic distance to reach the detector on the Earth. In this process,they pass through the SN matter and the Earth matter. During their propagation,SN neutrinos are subject to the Mikheyev–Smirnov–Wolfenstein(MSW)eあects,[17−18]the shock wave eあects,[19−20]the neutrino collective eあects,[21]and the Earth matter eあects.[9−10,22]Diあerent from the case in vacuum,the behavior of neutrino oscillation changes when neutrinos propagate in matter.The neutrino matter eあects,resulting from the interaction between matter and neutrinos,was found by Wolfenstein,Mikheyev,and Smirnov,then named as MSW eあects.Inside the SN,the large mixing angle solution of neutrinos results in the crossing probability,PL∼0,at the low resonance region.Therefore,we only need to consider the crossing possibility,PH,at the high resonanceregion.[18,23]Since the shock wave eあects may change the density profi le of SN as well as the position of the high resonance,and θ13is not as small as expected before,the expression of PHfor large θ13under the shock wave eあects needs to be further developed.[10,18,24]By scanning the ranges of relevant parameters in the neutrino spectra,it is possible to obtain the maximum and minimum event numbers of SN neutrinos detected on the Earth.

Table 1 Summary of experimental results about θ13.Numbers with(without)brackets are for normal(inverted)mass hierarchy.

This paper is organizedas follows.In Sec.2,we present a brief overview of SN explosions and the production of SN neutrinos.In Sec.3,we describe the four physical effects on the detection of SN neutrinos including the MSW eあects,the shock wave eあects,the neutrino collective effects,and the Earth matter eあects.In this section,how to obtain the expression of PHin the high resonance region for large θ13is presented in detail.In Sec.4,using the latest result of the Daya Bay experiment,θ13=8.8°± 0.8°,we take into account the four physical eあects and calculate the event numbers of SN neutrinos detected on the Earth.The results illustrate how the relevant SN neutrino parameters impact on the variation of event numbers and how many SN neutrinos can be detected at the Daya Bay experiment.Finally,in Sec.5 we give the summary and discussions.

2 SN Explosions and SN Neutrino Spectra

According to the presence or absence of hydrogen lines in their spectra,supernovas can be classif i ed into two types,type I and type II.In this paper,we only pay attention to the type II supernovas,one main source of neutrinos in the universe,which are also named as core-collapse supernovas having hydrogen lines in their spectra.[25]The explosion process of core-collapse supernovas can be divided into several phases,and more details about the scenario of explosion can be found in Ref.[1].In recent years,some impressive progresses have been made on the simulations of the post-bounce core-collapse SN,indicating how the luminosities and energies of SN neutrinos change in the accretion and cooling phases.[26−27]

An SN explosion approximately releases a total energy of EB=3×1053erg,about 99%of which is radiated away as SN neutrinos.[28]The relation between the total SN energy and the luminosity of diあerent f l avor neutrinos is given by[29]

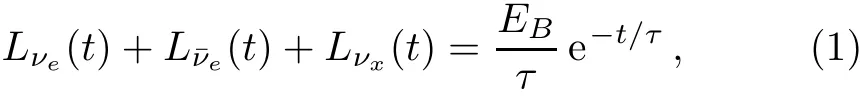
where νxrepresent νµ,ντ,¯νµ,and¯ντ.The luminosity f l ux of the SN neutrinos Lα(α=νe,¯νe,νx)decays in time as

The range of τ was obtained by f i tting the experimental data of SN1987A:τ=1.74–4.19 s.[28,30]

Basically,the SN neutrino spectra are parameterized to match the result of Monte Carlo simulations.Here,we use the “alpha f i t” distribution,which was given by the Garching group(we will call it “Garching” distribution later in this paper).It can be expressed as[31]

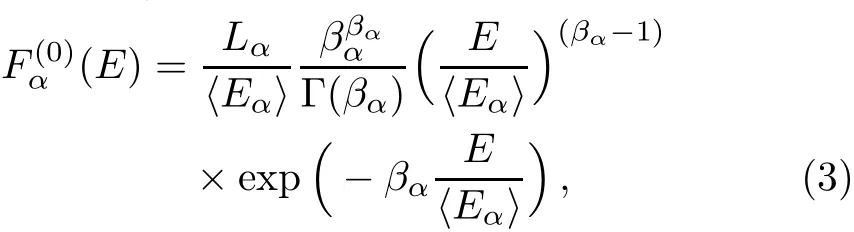
where 〈Eα〉is the average energy of neutrino and βαis the dimensionless pinching parameter.For diあerent neutrinos,their values are typically[1,32]

The ranges of luminosity ratios for diあerent f l avor neutrinos are the following in this model:

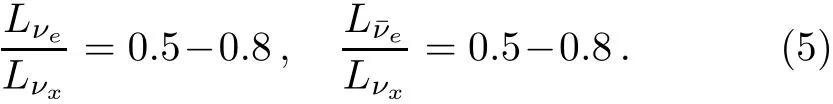
3 Four Physical Eあects on SN Neutrinos

When neutrinos propagate outward to the surface of SN,they can be subject to the SN shock wave eあects,the MSW eあects,and the collective eあects.Before arriving at the detectors,they travel through the Earth matter and are aあected by the Earth matter eあects.In this section,we will consider all the above four physical eあects on SN neutrinos.

3.1 MSW Eあects and Conversion Probability

The MSW eあects are caused by neutrino interactions with matter,which are determined by the matter den-sity prof i le and the mixing angles.By using the Landau’s method,the conversion probability PHfor neutrinos to jump from one mass eigenstate to another at the high resonance layer can be expressed as[18]

The factor F is given by

where neis the electron density,r is the distance to the center of SN,and the adiabaticity parameter γ is def i ned as[18]

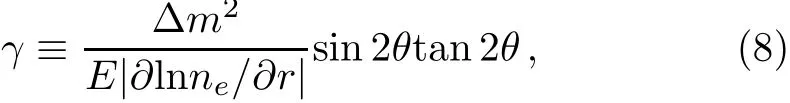
with Δm2being the mass square diあerence of two mass eigenstates.

For the SNs,n≈−3,the expression of F in the case of ne∝rnin Eq.(7)is

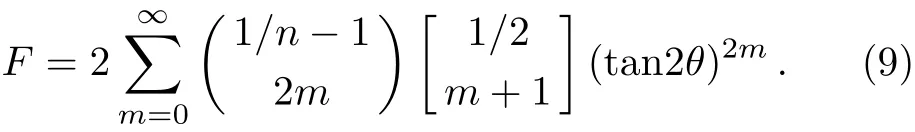
In Eq.(9)

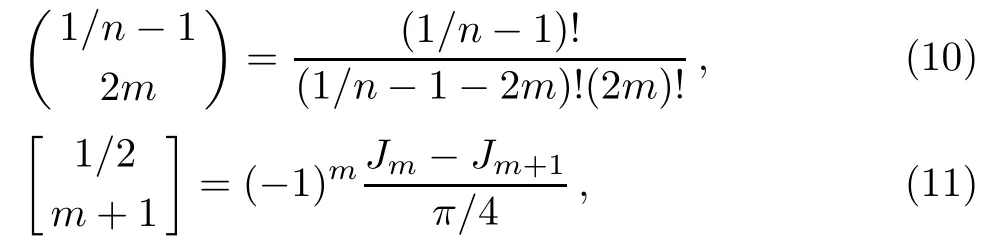
with

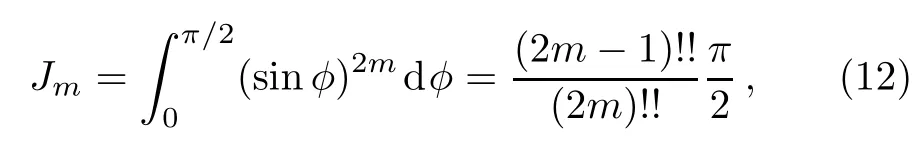
Eq.(9)can be expressed as a hypergeometric function:

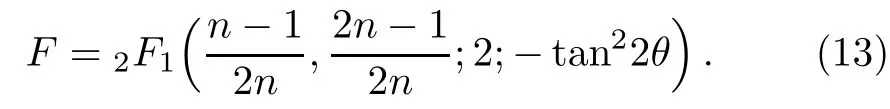
In the case of θ ∈ [0,π/8],using the Euler integral representation,[33]one has

We make the Taylor expansion for F near the point 1/n=0,

The f i rst two coeきcients in Eq.(15)can be obtained straightforwardly,

Comparing with the numerical result of the right-hand side of Eq.(14)in the case 1/n→0,we fi nd that the fi rst two terms in Eq.(15)give dominant contributions and other items are negligible,so F can be approximately written as the following equation,Eq.(17),which is identical to the expression in Ref.[18].

For the case of n=−3,the comparison between the numerical result of the right-hand side of Eq.(14)and that given by Eq.(17)is shown in Fig.1.It can be seen that for n=−3,Eq.(17)is a very good approximation to2F1in Eq.(14).

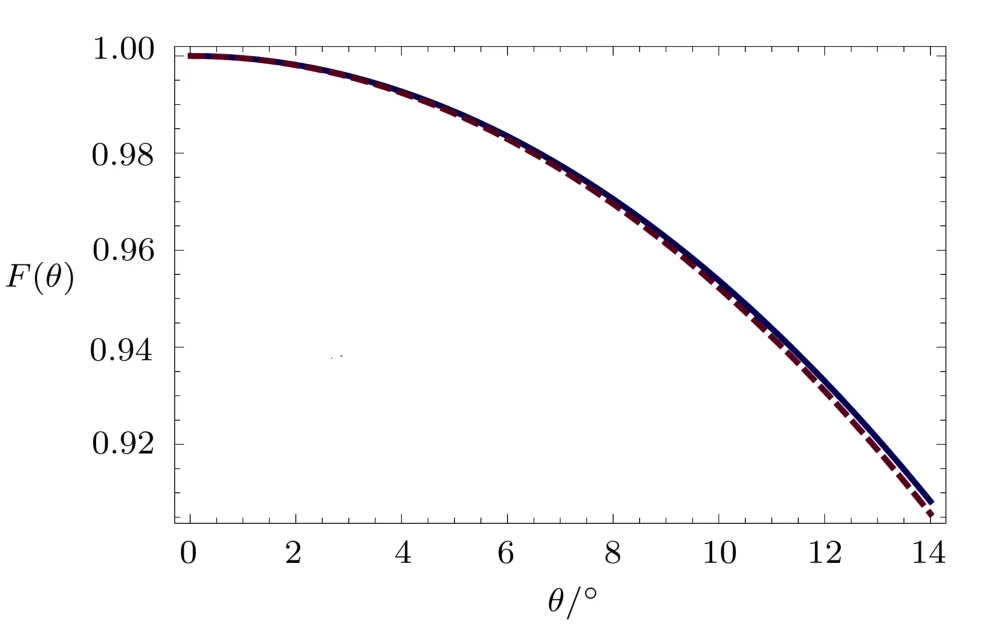
Fig.1 Numerical result of F as a function of θ for n=−3.The solid and dashed curves represent the results when F takes the expression of Eqs.(14)and(17),respectively.

3.2 SN Shock Wave Eあects and PH

The SN shock wave eあects play an important role in the SN neutrino oscillations.As pointed out in Ref.[34]and further studied in Refs.[35–37],after the core bounce,the shock wave propagates inside the SN during the period of neutrino emission and modi fi es the density profi le of the star.In several seconds,the forward shock wave may reach the resonance region where the conversion of diあerent fl avor SN neutrinos maximize,thus affecting the transition probability PHin the high resonance region.[19,23]Recent simulations indicate that reverse shock waves can be formed when the velocity of the material becomes larger than the local sound speed,therefore it can eあect the density as well.[38−39]It was also pointed out that the turbulence eあects should be included in the supernova simulations.[40]

In the following,we will consider the main character of shock wave eあects by taking into account the forward shock wave eあects,which are analytically approximated and characterized by a density jump as shown in Ref.[37].

In general,the density distribution of SN might be divided into two phases roughly by time:t＜ 1 s and t≥ 1 s.The changes of the density prof i le and the calculation expressions of PHunder the inf l uence of shock wave eあects were discussed in Refs.[10,37]in detail,and we refer the reader to these references.For post-bounce time t＜1 s,without shock wave eあects,the density prof i le can be approximated by its static limit ρ0as given by[34]

In Eq.(18)n=−2.4.It has been proven that in this case Eq.(17)is a very good approximation to Eq.(14).The diあerence between the numerical results from these two equations are negligible when θ13=8.8°.

Because the Daya Bay experimental result,θ13=8.8°± 0.8°,is quite diあerent from the condition θ13＜ 3°in Refs.[9–10],it is necessary to make clear the behavior of PHfor large θ13.In Eqs.(6)–(8),it can be found that PHdepends on F and γ,which are related to θ13and the neutrino energy E.In Figs.2,3,and 4,it is shown how the crossing probability PHchanges as a function of the neutrino energy E,the time t,and the mixing angle θ13,respectively.

Fig.2 The crossing probability at the high resonance region PHas a function of the neutrino energy E for three neutrino mixing angles at t=6 s.The solid,dashed,and dotted curves correspond to θ13=3°,6°,9°,respectively.

Fig.3 The crossing probability at the high resonance region PHas a function of the time t for three neutrino energies at θ13=9°.The solid,dashed,and dotted curves correspond to neutrino energy E=11,16,25 MeV,respectively.

Fig.4 The crossing probability at the high resonance region PHas a function of the neutrino mixing angle θ13:(a)for three diあerent times at E=11 MeV.The solid,dashed and dotted curves correspond to t=2 s,4 s,6 s,respectively;(b)for three diあerent neutrino energies at t=6 s.The solid,dashed,and dotted curves correspond to E=11,16,25 MeV,respectively.

In Fig.2,it can be seen that the value of PHdepends on the energy of SN neutrino.Whatever value θ13takes,the value of PHhas a great “jump” approximately at E=10 MeV.For θ13=3°,the curve of PHstill has obvious continuous f l uctuations from about 15 MeV to higher energy.For θ13=6°and θ13=9°,the value of PHchanges smoothly and decreases slowly when E≥30 MeV.Figure 3 shows the curves of PHfor three typical neutrino energies when the time ranges from 0 s to 10 s.We can see that as the energy increases the curve becomes fatter.In other words,the greater the neutrino energy,the longer time PHkeeps at high values.In general,the value of PHreaches the maximum value when the time is between 4–6 s.

In Fig.4(a),it is found that for a certain neutrino energy,at diあerent times,the value of PHchanges smoothly in the range of θ13=5°− 10°.However,the curve for t=6 s has rapid f l uctuations between 0°and 5°.In Fig.4(b),all the curves corresponding to three neutrino energies have obvious f l uctuations when θ13is between 0°and 5°.This is far from the real θ13value.Figures 2,3,and 4 illustrate that PHis zero near the real value of θ13(8.8°)when there are no shock wave eあects.However,when the shock wave eあects turn on PHis not zero in a range of time.

3.3 Collective Eあects and Earth Matter Eあects

The neutrino collective eあects,which mechanism is totally diあerent from that of the MSW eあects,are caused by the neutrino-neutrino interactions inside the core-collapse SN.Recently,it has been realized to be a crucial feature at very high densities of the core and can change the emitted fl uxes of diあerent fl avor neutrinos substantially.[21,32]

Up to now,there have been a signi fi cant amount of studies on the neutrino collective eあects.[21,29,32,41−45]In Ref.[32],it was shown that the collective eあects depend on the inherent features of SN neutrinos,such as their initial total energy,relative luminosities of diあerent fl avors,and the neutrino mass hierarchy.[1,46−47]In this paper,in order to study the collective eあects quantitatively,we set Pννas the survival probability that the neutrinos(antineutrinos)ν(ν¯)remain as their original states after the collective eあects.In Ref.[21]the authors introduced a simpli fi ed picture to describe the characteristics of the collective eあects:

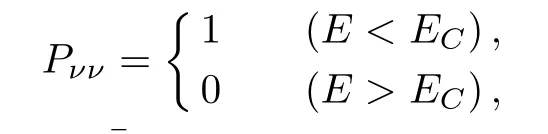
for neutrinos and¯Pνν=1 for antineutrinos,where ECis a critical energy.We take EC=10 MeV in our later calculation.[21]

When reaching the Earth,the neutrinos are mass eigenstates,then they oscillate in f l avors while going through the Earth matter.In Refs.[9–10],the authors studied Earth matter eあects in detail.For simplicity,we do not repeat it here but refer the reader to these references.

4 Detecting SN Neutrinos on the Earth

There are three reaction channels with which one may detect SN neutrinos at the Daya Bay experiment:the inverse beta decay,neutrino-electron reactions,and neutrino-carbon reactions.The reaction formulas and the means of calculation were discussed in Refs.[9–10]and the relevant eあective cross sections mentioned in Refs.[48–49]are still applicable when θ13is large.

4.1 Calculation of Event Numbers

A detailed description of the Daya Bay experiment can be found in Refs.[50–51].There are eight detectors located at diあerent sites of the Daya Bay experiment.The total detector mass is about 300 tons and the depth of the detectors h≃400 m.The Daya Bay Collaboration uses Linear Alkyl Benzene(LAB)as the main part of the liquid scintillator.LAB has a chemical composition including C and H with the ratio of the number of C and H being about 0.6.Then,the total numbers of target protons,electrons,and12C areWith all of the four physical eあects being taken into account,the SN neutrino f l uxes at the detector are expressed as

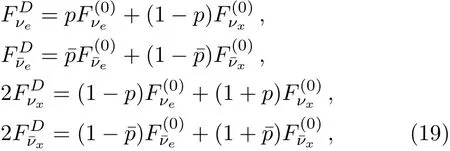
where the survival probabilities p and¯p are given by

for the normal mass hierarchy and

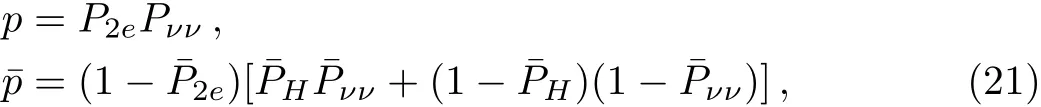
for the inverted mass hierarchy.P2eis the probability that a neutrino mass eigenstate enters the surface of the Earth and arrives at the detector as an electron neutrino νe.[52]

The event numbers N(i)of SN neutrinos in the reaction channel“i” can be calculated by integrating over the neutrino energy,the product of the target number NT,the cross section of the given channel σ(i),and the neutrino fl ux function at the detector FαD,

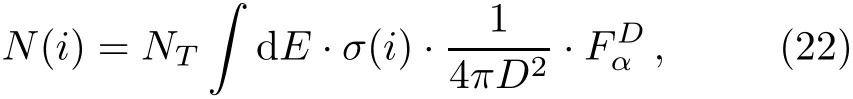
where α stands for the neutrino or antineutrino of a given fl avor,and D is the distance between the SN and the Earth.[9]

4.2 Scanning over the Relevant Parameters

In Sec.2,we gave the ranges of the average energies of neutrinos〈Eα〉and ranges of dimensionless pinching parameters βαin the parametrization of SN neutrino f l uxes as listed in Eq.(4).It is expected to obtain the maximum and minimum values of neutrino event numbers in the Daya Bay experiment from our calculation results.To achieve this objective,scanning over the ranges of all the parameters related to the calculation of four physical effects on detecting SN neutrinos is necessary.Notice that the luminosity ratios of diあerent f l avor neutrinos in Eq.(5)should be considered as well.In fact,as will be shown in the next subsection,the luminosity ratios do have eあects on neutrino event numbers.

Comparing the three reaction channels,it can be seen that the cross sections for the neutrino-electron scattering channel(∼ 10−45)are much smaller than the other two reaction channels(∼ 10−43).[9]Hence,we will only consider the inverse beta-decay and the neutrino-carbon reactions in the following analysis.It also can be seen that the inverse beta-decay does not involve any parameters about νesince νeis not involved in the inverse beta-decay.Based on simulation results the luminosity of νeand¯νecan be taken to be equal,[31]so we can def i ne

Scanning over the ranges of all the parameters in Eqs.(4)and(5),we obtain the following parameter values for the distribution in Eq.(3):

for the inverse beta decay,and

for the neutrino-carbon reactions.

From Eq.(5)it can be seen that M varies between two extreme values,1.25 and 2.In order to see the inf l uence of the luminosity ratio itself on event numbers,we only change the values of M in Eqs.(24)–(27)to the other extreme values,with keeping 〈Eα〉and βαunchanged,then we obtain the following comparison groups of parameters for Eqs.(24)–(27),respectively:

for the inverse beta decay,and

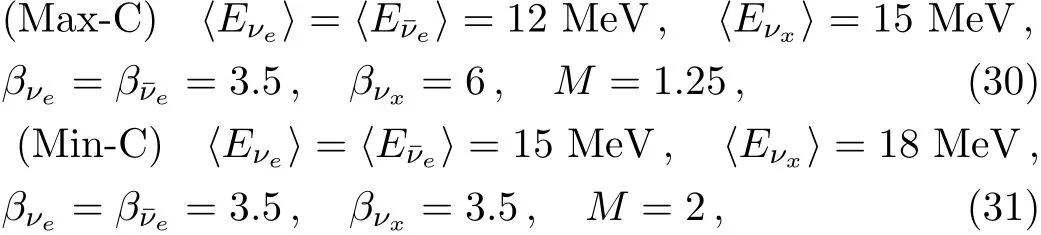
for the neutrino-carbon reactions.It is noted that no matter how the value of M changes,the total energy of all f l avor neutrinos is a constant and the results with parameters in comparison groups are always between the maximum and minimum event numbers.

4.3 The SN Neutrino Event Numbers under the Inf l uence of Four Physical Eあects

In this subsection,we give the numerical results of SN neutrino event numbers detected at the Daya Bay experiment.Consider a “standard” supernova at a distance D=10 kpc from the Earth,which releases total energy EB=3×1053erg,and take τ=3 s as the decay time of its luminosity.[28−30]The values of relevant parameters have already been given in the previous subsections.Given the Daya Bay experimental result,we take θ13=8.8°in our calculations.

With the inf l uence of all the four physical eあects being taken into account,supposing a neutrino reaches the detector with the incident angle α,[9−10]we calculate the neutrino event numbers with the neutrino spectra of the“Garching” distribution and plot the neutrino event numbers N as a function of α in Figs.5 and 6 for the inverse beta-decay and the neutrino-carbon interactions,respectively.In order to show the inf l uence of the luminosity ratio conveniently,the results of two groups with the same〈Eα〉and βαbut diあerent M are plotted in the same f i gures.For example,in Fig.5(a)there are four styles of numerical curves representing the results of“Max” (M=2)and “Max-C”(M=1.25)for both normal and inverted mass hierarchies.

Generally speaking,the maximum variation of neutrino event numbers appears at α ∼ 93°when α changes due to the Earth matter eあects for both reactions.Meanwhile,the variations in the inverse beta-decay are more obvious than those in the neutrino-carbon reactions.Also for both reactions,the numerical results show signif i cant diあerences between the normal hierarchy and the inverted hierarchy even for the same values of 〈Eα〉and βαand the same luminosity ratio M.For example,comparing the solid curve(normal)and the dashed curve(inverted)in Fig.5(a),it can be seen that the distance between the two curves are roughly 60 although they have the same parameter values as listed in Eq.(24).This point shows that event numbers largely depend on the mass hierarchy.

On the other hand,it is found that even with the same values of〈Eα〉and βαand with the same mass hierarchy,event numbers still change with the luminosity ratio M.For instance,in Fig.6(a),the solid curve(M=2)is about 15 more than the dotted curve(M=1.25)although they both correspond to the normal hierarchy and the same〈Eα〉and βαas listed in Eqs.(26)and(30).However,we should note that in Figs.5(a)and 5(b),the solid curves(normal)are very close to the dotted curves(normal)and the diあerence between them is less than about 3.By contrast,the diあerence between the dashed curves(inverted)and dot-dashed curves(inverted)in Figs.5(a)and 5(b)is signif i cantly greater,which is more than 20.This shows that for the inverse beta-decay reaction,if the mass hierarchy is normal,event numbers change in a relatively narrow range over the values of M,while if the mass hierarchy is inverted,this is not the case.For the neutrinocarbon interaction in Figs.6(a)and 6(b),it is shown that the variations of event numbers are remarkable with the changes of luminosity ratio no matter which mass hierarchy it is.Based on the above analysis,it is obvious that the luminosity ratio M plays an important role in determining the event numbers.

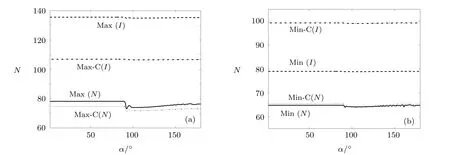
Fig.5 The event numbers for the inverse beta-decay with the parametrization form in Eq.(3). “α” is the incident angle of the SN neutrino reaching the detector. “N(I)” represents normal(inverted)mass hierarchy.In Fig.5(a)“Max” and “Max-C” correspond to parameter values listed in Eqs.(24)and(28),respectively;in Fig.5(b)“Min” and “Min-C” correspond to parameter values listed in Eqs.(25)and(29),respectively.

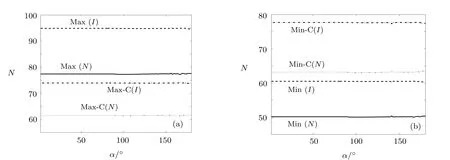
Fig.6 The event numbers for the neutrino-carbon interactions with the parametrization form in Eq.(3).“α” is the incident angle of the SN neutrino reaching the detector. “N(I)” represents normal(inverted)mass hierarchy.In Fig.6(a)“Max” and “Max-C” correspond to parameter values listed in Eqs.(26)and(30),respectively;in Fig.6(b)“Min” and “Min-C” correspond to parameter values listed in Eqs.(27)and(31),respectively.

The summary of event numbers for the two reaction channels with the“Garching”distribution are given in Tables 2 and 3.The numerical results illustrate that the event numbers and the change rates due to the Earth matter eあects depend on the parameters 〈Eα〉and βα,as well the mass hierarchy.Furthermore,the luminosity ratio M has an important inf l uence on the event numbers and the change rates while other parameters remain unchanged.Comparing the results with the “Min” and“Min-C”groups of parameters for the inverse beta-decay,for example,in the case of inverted mass hierarchy,when M=1.25 the event numbers at the incipient angle and the change rates are 78.98 and 0.18%,respectively;while when M=2 these two corresponding numbers are 99.31 and 0.30%,both of which are signif i cantly more than the former two.For another example,focusing on the results of the“Max”and“Max-C”groups of the neutrino-carbon interactions,in the case of normal mass hierarchy,when M=1.25 the event numbers at the incipient angle and the change rates are 61.49 and 0.15%,respectively;while when M=2 these two numbers are 77.4 and 0.22%,respectively,which are also much larger.

Table 2 Summary of event numbers of the inverse beta-decay for the parametrization form given in Eq.(3).“Max” and “Max-C” correspond to parameter values in Eqs.(24)and(28),respectively;“Min” and “Min-C”correspond to parameter values in Eqs.(25)and(29),respectively. “N(I)” represents normal(inverted)mass hierarchy.The numbers in the columns “Incipient” and “Min” are the event numbers when the SN neutrino incident angle is zero and is the angle in the column “Angle”,respectively.The column “Angle” gives the angles at which the event numbers are the minimum and the Earth matter eあects are the strongest. “Ratio” gives the percentages of the Earth matter eあects.

Table 3 Summary of event numbers of the neutrino-carbon interaction for the parametrization form given in Eq.(3). “Max” and “Max-C” correspond to parameter values in Eqs.(26)and(30),respectively;“Min” and“Min-C” correspond to parameter values in Eqs.(26)and(30),respectively.“N(I)” represents normal(inverted)mass hierarchy.The numbers in the columns“Incipient” and “Min” are the event numbers when the SN neutrino incident angle is zero and is the angle in the column “Angle”,respectively.The column “Angle” gives the angles at which the event numbers are the minimum and the Earth matter eあects are the strongest. “Ratio” gives the percentages of the Earth matter eあects.

Table 4 The event number ranges in the Daya Bay experiment with all the uncertainties taken into account.“N(I)” represents normal(inverted)mass hierarchy.

In Table 4 we give neutrino event numbers detected at the Daya Bay experiment when all the uncertainties are taken into account in the cases of normal and inverted mass hierarchies,respectively.We can see that the event numbers range from 63.66∼135.58 and 50.05∼94.9 for the inverse beta-decay and the neutrino-carbon interactions,respectively.

5 Summery and Discussions

Given the new experimental result about θ13from the Daya Bay Collaboration,we deduce the expression of the neutrino conversion probability in the high resonance region inside SN,PH,in the case of large θ13(≃ 8.8°),by applying the available knowledge for PH.PHis expressed in the form of hypergeometric function.In the derivation,we take the shock wave eあects into account.Furthermore,we give numerical results of PHas functions of θ13,t,and E.It is found that PHis zero near the real value of θ13when there are no shock wave eあects.However,it is not zero in a certain region of time(roughly 3 s∼8 s depending on neutino energies)if the shock wave eあects are considered.Our work is diあerent from previous studies which were usually done in the case of small θ13(＜ 3°).[9−10]

We consider the inf l uence of all the four physical eあects on the detection of SN neutrinos,including the MSW effects,the SN shock wave eあects,the neutrino collective eあects,and the Earth matter eあects.Scanning over all the relevant parameters in the form of“Garching” neutrino energy distribution,we calculate the event numbers for two reaction channels,the inverse beta-decay and the neutrino-carbon reactions,both of which can be detected at the Daya Bay experiment.It is found that the event numbers depend on the parameters 〈Eα〉, βα,and Lα,as well as the mass hierarchy.We emphasize that the event numbers depend on the luminosity ratio substantially.This point has not been discussed before.Finally,we give the range of SN neutrino event numbers detected at the Daya Bay experiment.

Although a lot of eあort has been made on identifying the four physical eあects on detection of SN neutrinos,there are still a lot of problems,which need to be solved.One example is the neutrino collective eあects in the case of large θ13.Progress in this direction will aあect the detection of SN neutrinos.Now the Daya Bay II experiment is under consideration.Its detector mass will be about 70 times of the total detector mass of the Daya Bay experiment.This will make it much more possible to detect SN neutrinos in the future.

[1]K.Kotake,K.Sato,and K.Takahashi,Rept.Prog.Phys.69(2006)971.

[2]S.Akiyama,J.C.Wheeler,D.L.Meier,and I.Lichtenstadt,Astrophys.J.584(2003)954.

[3]H.A.Bethe,Rev.Mod.Phys.62(1990)801;G.E.Brown,H.A.Bethe,and G.Baym,Nucl.Phys.A 375(1982)481.

[4]J.M.Lattimer and M.Prakash,Astrophys.J.550(2003)426.

[5]J.M.Bardeen,B.Carter,and S.W.Hawking,Commun.Math.Phys.31(1973)161.

[6]D.Lal,Earth and Planetary Science Letters 104(1991)424.

[7]W.D.Arnett,Astrophys.J.A 319(1987)136.

[8]R.M.Bionta,G.Blewitt,C.B.Bratton,D.Casper,A.Ciocio,et al.,Phys.Rev.Lett.58(1987)1494.

[9]X.H.Guo,M.Y.Huang,and B.L.Young,Phys.Rev.D 79(2009)113007.

[10]M.Y.Huang,X.H.Guo,and B.L.Young,Phys.Rev.D 82(2010)033011.

[11]F.Ardellier and I.Barabanov,et al.,[arXiv:hep-ex/0606 025].

[12]J.M.Wang,et al.,Astrophy.J.Lett.701(2009)7.

[13]K.Abe,et al.,Phys.Rev.Lett.107(2011)041801.

[14]P.Adamson,et al.,Phys.Rev.Lett.107(2011)181802.

[15]F.P.An,et al.,[Daya-Bay Collaboration],Phys.Rev.Lett.108(2012)171803.

[16]Y.Abe,et al.,Phys.Rev.Lett.108(2012)131801.

[17]L.Wolfenstein,Phys.Rev.D 17(1978)2369;ibid.20(1979)2634.

[18]T.K.Kuo and J.Pantaleone,Rev.Mod.Phys.61(1989)937.

[19]T.Takiwaki,et al.,Astrophys.J.616(2005)1086.

[20]G.L.Fogli,et al.,J.Cosmol.Astropart.Phys.0504(2005)002.

[21]B.Dasgupta and A.Dighe,Phys.Rev.D 77(2008)113002.

[22]C.Lunardini and A.Y.Smirnov,Nucl.Phys.B 616(2001)307.

[23]S.P.Mikheyev and A.Y.Smirnov,Nucl.Phys.B 42(1985)913.

[24]M.Kachelriess,A.Strumia,R.Tomas,and J.W.F.Valle,Phys.Rev.D 65(2002)073016.

[25]T.J.Loredo and D.Q.Lamb,Phys.Rev.D 65(2002)063002.

[26]L.Hudepohl,et al.,Phys.Rev.Lett.104(2010)251101.

[27]S.Chakraborty,et al.,Phys.Rev.D 84(2011)025002;Phys.Rev.Lett.107(2011)151101.

[28]D.N.Spergel,et al.,Science 237(1987)1471.

[29]G.L.Fogli,et al.,J.Cosmol.Astropart.Phys.0904(2009)030.

[30]T.J.Loredo and D.Q.Lamb,et al.,Acad.Sci.571(1989)601;T.J.Loredo and D.Q.Lamb,Phys.Rev.D 65(2002)063002.

[31]M.T.Keil and T.U.Munchen,Preprint[astro-ph/0308 228];M.T.Keil,et al.,Astrophys.J.590(2003)971.

[32]S.Chakraborty and S.Choubey,et al.,J.Cosmol.Astropart.Phys.1006(2010)007.

[33]A.P.Prudnikov,Yu.A.Brychokov,and O.I.Marichev,Integrals and Series,Gordon and Breach,New York(1990).

[34]R.C.Schirato and G.M.Fuller,Preprint[astro-ph/0205 390](2002).

[35]K.Takahashi,et al.,Astropart.Phys.20(2003)189.

[36]R.Tomas,et al.,Astropart.Phys.0409(2004)015.

[37]G.L.Fogli,E.Lisi,A.Mirizzi,and D.Montanino,Phys.Rev.D 68(2003)033005.

[38]J.P.Kneller,G.C.McLaughlin,and J.Brockman,Phys.Rev.D 77(2008)045023.

[39]S.Galais,et al.,Phys.Rev.D 81(2010)053002.

[40]T.Lund and J.P.Kneller,Phys.Rev.D 88(2013)023008,[arXiv:1304.6372[astro-ph.HE]].

[41]H.Y.Duan and J.P.Kneller,J.Phys.G 36(2009)113201.

[42]H.Y.Duan,G.M.Fuller,and Y.Z.Qian,Phys.Rev.D 74(2006)123004;ibid.76(2007)085013;ibid.75(2007)125005;Phys.Rev.Lett.99(2007)241802.

[43]S.Hannestad,G.G.Raあelt,G.Sigl,and Y.Y.Y.Wong,Phys.Rev.D 74 (2006)105010; ibid.76 (2007)029901(E).

[44]G.G.Raあelt and A.Y.Smirnov,Phys.Rev.D 76(2007)081301(R);ibid.76(2007)125008.

[45]G.L.Fogli,E.Lisi,et al.,J.Cosmol.Astropart.Phys.0712(2007)010;0910(2009)002.

[46]C.Lunardini and A.Y.Smirnov,J.Cosmol.Astropart.Phys.0306(2003)009.

[47]K.Takahashi and K.Sato,Prog.Theor.Phys.109(2003)919.

[48]L.Cadonati,F.P.Calaprice,and M.C.Chen,Astropart.Phys.16(2002)361.

[49]A.Burrows,S.Reddy,and T.A.Thompson,Nucl.Phys.A 777(2006)356.

[50]F.P.An,et al.,[Daya-Bay Collaboration],Nucl.Instrum.Meth.A 685(2012)1.

[51]X.H.Guo,et al.,[Daya-Bay Collaboration],[arXiv:hepex/0701029].

[52]A.N.Ioannisian and A.Yu.Smirnov,Phys.Rev.Lett.93(2004)241801;A.N.Ioannisian,et al.,Phys.Rev.D 71(2005)033006.