Robust Quantum Computing in Decoherence-Free Subspaces with Double-Dot Spin Qubits∗

FENG Zhi-Bo(冯志波), ZHANG Chun-Li(张春丽),and ZHOU Yun-Qing(周运清)

1School of Electric Engineering,Xuchang University,Xuchang 461000,China

2Department of Physics,Zhejiang Ocean University,Zhoushan 316000,China

1 Introduction

With theoretical signif i cance and practical applications,quantum information processing has been a fascinating research f i eld.[1]As solid-state artif i cial atom,semiconductor quantum dot can be manipulated controllably and scaled up easily,then it is one of the most promising candidates for quantum state engineering.[2−3]Based on the electronic spin degrees of freedom,double-dot qubits have made remarkable progress on coherent manipulations and precise readouts of quantum states.[4−5]In the past few years,one-dimensional transmission line resonator(TLR)on a chip has attracted particular attention.[6−7]The quantized cavity f i eld generated by the TLR can be coupled to semiconductor quantum dots,which thus forms a circuit quantum electrodynamics(QED)device.[8−12]Very recently,the strong couplings between semiconductor quantum dots and superconducting microwave cavity have been realized experimentally,[13−16]which are very helpful to perform quantum information processing with hybrid systems.

For semiconductor spin-based qubits,decoherence effect is still one of the main obstacles to build a quantum computer.[1,17−18]Many fault-tolerant strategies for removing noise eあects have been proposed,such as geometric quantum computing,[19]dynamical decoupling,[20]and optimal operation.[21]As a quantum error-avoiding way,decoherence-free subspace(DFS)encoding can be resistant to the collective noises according to the symmetry of system-bath interaction.[22−25]Especially,the DFS encoding may be a more robust approach to f i ght against quantum errors,when the decoherence eあects are caused mainly by the collective noises in a multiqubit system.However,how to physically perform the DFS-encoded logic gates on double-dot qubits is highly desirable for fault-tolerant quantum computing.

In this paper,we propose a theoretical scheme for performing robust quantum gates on the DFS-encoded qubits inside a circuit QED architecture.Through the TLR-assisted interaction,the couplings between any pair of qubits can be realized controllably and selectively,by which we construct a set of universal quantum gates on the DFS-encoded qubits.It is found that the gate f i delities can be enhanced remarkably by eliminating the collective noises.The proposal may provide the potential opportunity of implementing the robust quantum computing with solid-state hybrid systems.

The rest of paper is organized as follows.In Sec.2,many semiconductor double-dots in a circuit QED are illustrated.In Sec.3,we present the controllable interqubit couplings. Logic quantum gates on the DFS-encoded qubits are given in Sec.4.We analyze the f i delity enhancement by DFS-encoding way in Sec.5.Finally,discussion and conclusion are drawn in Sec.6.

2 Double-Dot Qubits in a Circuit QED

As schematically depicted in Fig.1(a),a high Q onedimensional TLR(of length Lxalong the x direction)has a single-mode frequency ωr.[9,26]Many semiconduc-tor double-dot systems are arranged along the x direction.The k-th double-dot is electrically coupled to the TLR via capacitance Ck,k=1,2,...,n.Through a capacitor Ci(Co),the TLR is connected to the input(output)wiring of the waveguide.[9−10]In the considered circuit QED device,the TLR generates a quantized standing-wave f i eld.Here the quantum dots are all situated at the antinodes to achieve the maximum coupling strengths between the dots and the cavity f i eld.Each double-dot includes two adjacent quantum dots,in which two electrons exist totally.And the double-dots are electrically biased to create potential diあerences Δ.[9,12]

For the operated double-dot,an external f i eld Bz(≈100 mT)is applied along the z axis.The spin parallel states[|(1,1)T+〉=|↑↑〉,|(1,1)T−〉=|↓↓〉]are split from the spin antiparallel ones[|(1,1)T0〉=(|↑↓〉+|↓↑〉)/|(1,1)S〉=(| ↑↓〉− | ↓↑〉)/],where(nu,nd)denotes nu(nd)electrons localized in the up(down)dot,T±,0stand for spin-triplet states,S denotes a spin-singlet one.[9−10]The doubly occupied state|(0,2)S〉is coupled to|(1,1)S〉only,whose tunneling energy is T,see Fig.1(b),and the potential diあerence between them is Δ.Due to the Pauli spin blockade,the coupling between|(0,2)S〉and|(1,1)T0〉is suppressed eあectively.[27−28]In the considered subspace{|(1,1)S〉,|(0,2)S〉},the system Hamiltonian is reduced to[9−10]

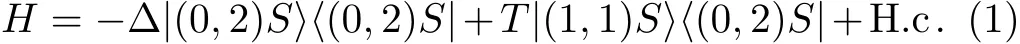
The eigenstates of Hamiltonian of Eq.(1)are|+〉=sinα|(0,2)S〉+cosα|(1,1)S〉and|−〉=cosα|(0,2)S〉−sinα|(1,1)S〉,with α =tan−1[−2T/(+ Δ)].The above Hamiltonian can be rewritten as H= ħωσz/2,in which the transition frequency between|−〉and|+〉is ω(= ω−− ω+)=/ħ,ω−(ω+)is the eigenfrequency of the level state|−〉(|+〉),and σz=|−〉〈−|−|+〉〈+|is a Pauli operator.With the experimentally available parameters,the dependences of ωjon Δ are shown in Fig.1(c),where T/2π =1.5 GHz is f i xed,j= −,+.At the optimal working point Δ=0,the states

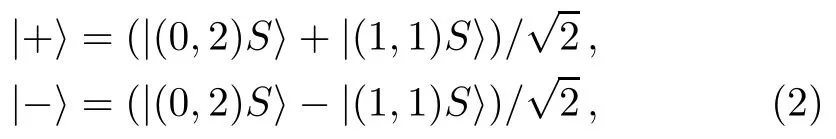
constitute the spin-based qubit states,which are insensitive to the f l uctuations of control electronics.[9]

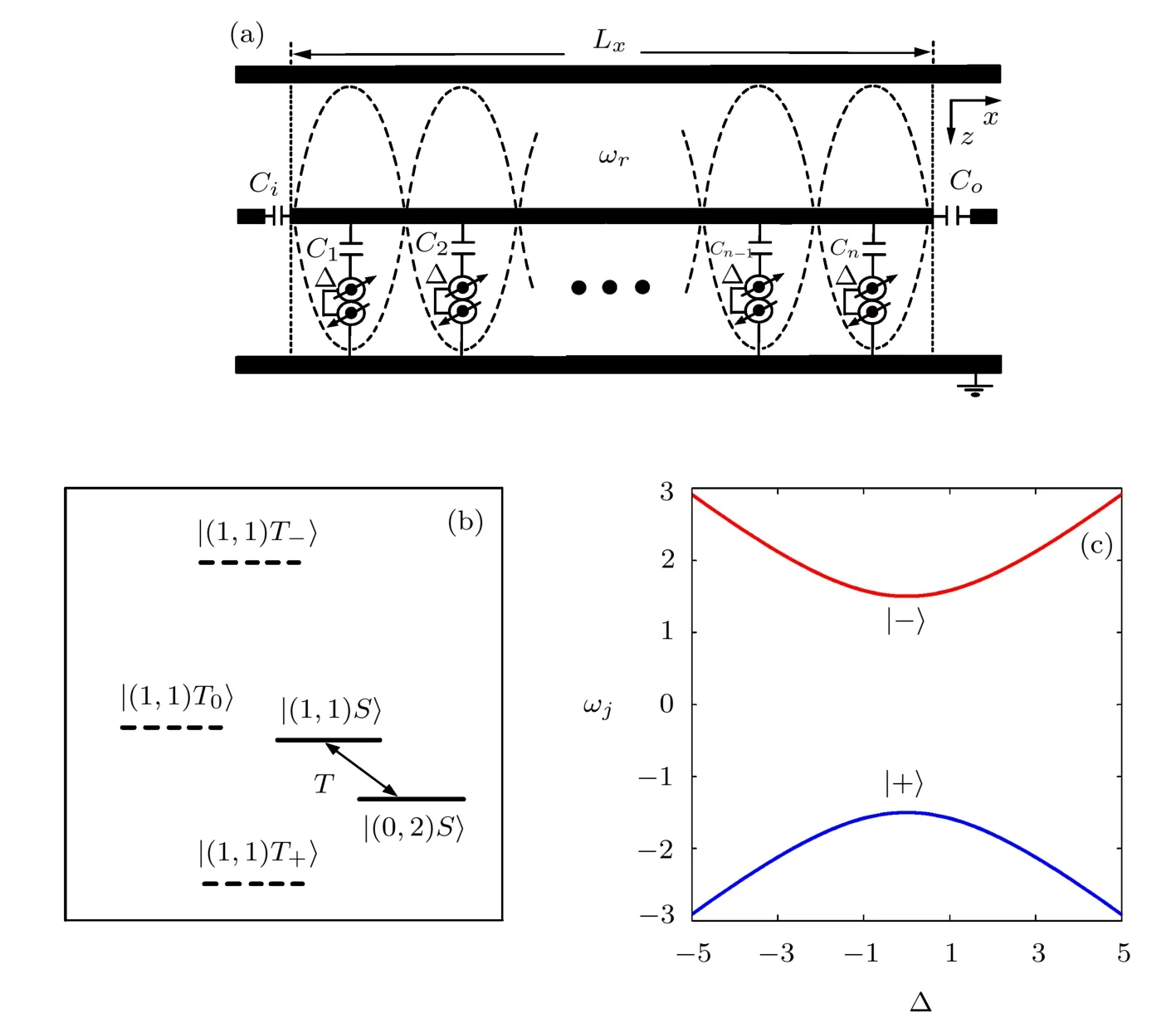
Fig.1 (a)Many double-dots are coupled to a one-dimensional TLR.(b)Level structure associated with spin states in a double-dot system.(c)Eigenfrequencies ωjof level states|j〉vs.potential diあerence Δ,with j= −,+.ωjand Δ are given in units of 2π GHz.

3 Controllable Interqubit Couplings

Through the gate capacitance Ck,the k-th double-dot situated at the antinode interacts with the quantized cavity f i eld.Under the rotating wave approximation,the interaction Hamiltonian within the basis{|+〉k,|−〉k}is given by[12,29]Hrk=ħλk(a†σ−k+aσ+k),the coupling strength is λk=(eCk/2ħCkt)with Cktbeing the total capacitance of the double-dot,a†(a)denotes the creation(annihilation)operator associated with photon,σ−k=|+〉k〈−|and σ+k=|−〉k〈+|represent the level inversion operators.For simplicity,the coupling coeきcients λkare assumed to be identical hereafter,namely,λk= λ.

Consider any two qubits,say k=1,2.The total Hamiltonian of the composite system involving the two qubits and cavity f i eld is described by HΣ=H0+H′,[29]where H0= ωra†a+ ω1σ1z/2+ ω1σ2z/2,and H′=δ12σ2z/2+ ∑k=1,2(λa†σ−ke−iδkt+H.c.),with ω1,2being the respective transition frequencies of qubits 1 and 2,a detuning is δ12= ω2− ω1,and we take ħ =1.In the dispersive regions,the detunings are much larger than coupling strengths,δ1r,2r(=|ω1,2− ωr|)≫ λ.Given the cavity f i eld is initially in the vacuum state,H′can be further transformed into the eあective Hamiltonian[30]

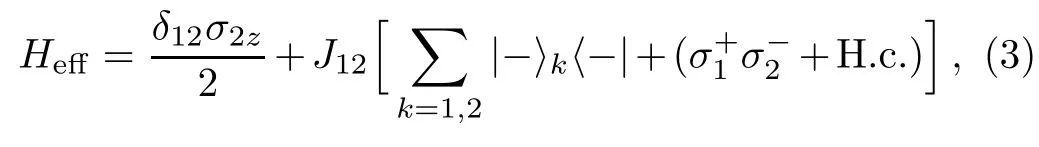
where the coupling strength isJ12= λ2(δ1r+δ2r)/(2δ1rδ2r).Through the cavity-mediated interaction,the interqubit coupling can be realized eあectively.

The states of qubits 1 and 2 span a product space as{|jj′〉},with j′=+,−.For an arbitrary state vector,it can be expressed as ψ(t)= ∑ Cjj′|jj′〉,where Cjj′ are the normalization coeきcients.The time evolution of ψ(t)is governed by the diあerential equation,i(dψ(t)/dt)=Heあψ(t).We focus on the dependence of coherent transition between|+−〉and|−+〉on the detuning δ12.Physically,with the f i xed transition frequency ω1,the changeable parameter δ12can be obtained only by tuning ω2.

Utilizing the experimentally feasible parameters,ω1/2π =5 GHz, ωr/2π =6.75 GHz[15]and λ/2π =0.125 GHz,[9]we numerically calculate the occupied probabilities of states|+−〉and|−+〉versus the detuning δ12.Note that we consider the maximum probability of|−+〉and the minimum one of|+−〉,and postulate that the initial state is|+ −〉.After a specif i c evolution time tn(=π/2J12)=28 ns,the occupied probabilities of|+−〉and|− +〉,as represented in Fig.2,depend on the detuning δ12remarkably.When δ12=0,the system is in|−+〉completely.The probability of|−+〉will be reduced greatly with increasing δ12.As demonstrated in the subf i gure,the probability of|−+〉is less than 4.25×10−3when δ12is in the large detuning region(δ12/2π ≥ 0.3 GHz).

From the viewpoint of coherent control,the interqubit coupling can be switchable eあectively by adjusting the detuning δ12.[31]When the transition frequencies are resonant with each other,the interqubit coupling exists.On the other hand,the coupling gets vanished at the large detuning δ12.At the same time,we can operate qubits selectively.Towards the practical quantum computing,the controllable and selective interqubit coupling is desirable to f l exibly manipulate the multiqubit system.

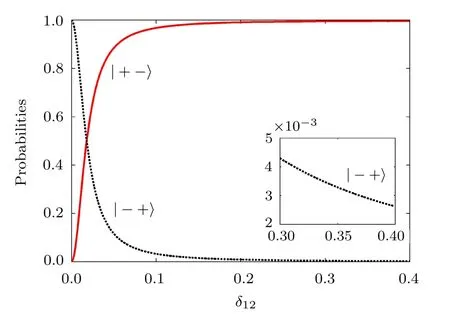
Fig.2 The occupied probabilities of states|−+〉and|+ −〉as functions of detuning δ12for a given evolution time,the unit of δ12is 2π GHz.

4 Quantum Gates on DFS-Encoded Qubits

As mentioned before,the two qubits 1 and 2 span a Hilbert space{|jj′〉},from which we select a subspace{|+ −〉,|− +〉},and encode the logic qubit states as|0〉L=|+ −〉and|1〉L=|− +〉,respectively.Owing to the symmetry of system-bath interaction,the subspace can be insensitive to certain collective noises,[22]which is thus referred to as decoherence-free subspace(DFS).The considered DFS{|+ −〉,|− +〉}is immune to σz-type collective noises.[32]Energy relaxation and dephasing are two factors that induce qubit decoherence.It is found that the dephasing eあect is dominant over the energy relaxation for the semiconductor spin qubit.Generally,the f l uctuations of nucleus spin and external f i elds with low frequencies give rise to the dephasing eあect.[30,33]The present DFS-encoded approach is just helpful to avoid the dephasing eあects caused by the collective noises.

In the following,taking advantages of the controllable interqubit coupling,we construct the universal logic gates on the DFS-encoded qubits.Firstly,we perform singlelogic-qubit gates.Adjust ω2to make ω2= ω1,and therefore the detuning is δ12=0.From Eq.(3),the evolution operator in the logic qubit basis{|0〉L,|1〉L}is obtained as[32]

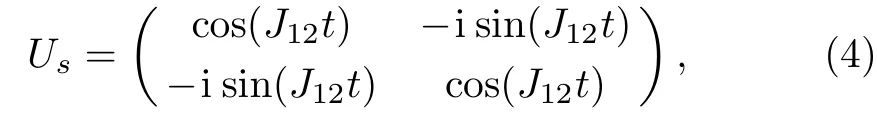
where the identical phase factors e−iJ12tregarding|0〉Land|1〉Lhave been left out.Obviously,two noncommutable single-logic-qubit gates can be achieved by controlling the diあerent evolution times.

Next we execute a two-logic-qubit conditional gate.Choosing other two physical qubits 3 and 4,we encode similarly the logic-qubit states as|0〉L=|+ −〉and|1〉L=|− +〉.Thus the DFS-encoded logic-qubit states are|00〉LL=|+ −〉|+ −〉,|01〉LL=|+ −〉|− +〉,|10〉LL=|− +〉|+ −〉,and|11〉LL=|− +〉|− +〉.By means of an auxiliary state|+〉5of qubit 5,we can perform a controlled-phase gate on the selected logic-qubits.[34]When the transition frequencies satisfy ω5= ω3= ω1,the eあective Hamiltonian of the three-qubit system is expressed as[34]

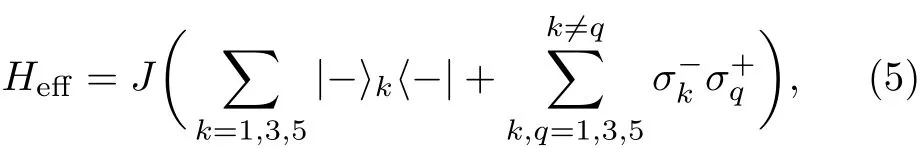
where the coupling strengths are J(=J13=J15=J35).According to Hamiltonian(5),the auxiliary qubit 5 is decoupled from the other qubits after a duration time tcp=2π/3J.Then the controlled-phase gate on the logic qubits is achieved as[32]

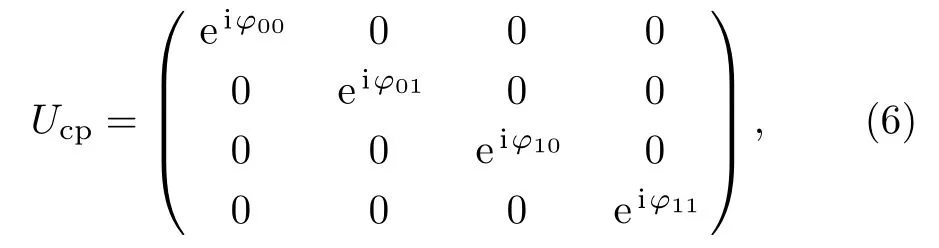
with ϕ00= ϕ01= ϕ10=0 and ϕ11= −2π/3.

So far,by virtue of the controllable interqubit couplings,we have obtained a set of universal logic gates on the DFS-encoded qubits,containing two noncommutative single-logic-qubit gates and a two-logic-qubit conditional gate.

5 Fidelity Enhancement by DFS-Encoding Qubits

In the multiqubit system,environmental noises acting upon qubits can be usually divided into the individual noises and the collective ones.[32]Since the DFS-encoded qubits are immune to the collective noises,the corresponding decoherence eあects can be eliminated naturally,which is extremely useful to obtain the fault-tolerant gate operations.The decoherence eあects on qubits can be simulated numerically by gate f i delity.As in Ref.[35],we have the f idelity F=where|ψi〉is an ideal output state without the noise eあects,ρ =|ψ〉〈ψ|indicates the reduced density matrix associated with a realistic state|ψ〉.And the time evolution of the density matrix can be addressed by the quantum theory of damping.

Here take the not-gate as an example to consider the robustness of the DFS-encoded way.The dynamical evolution of the reduced density matrix ρ is described by the Lindblad-type master equation,[36]

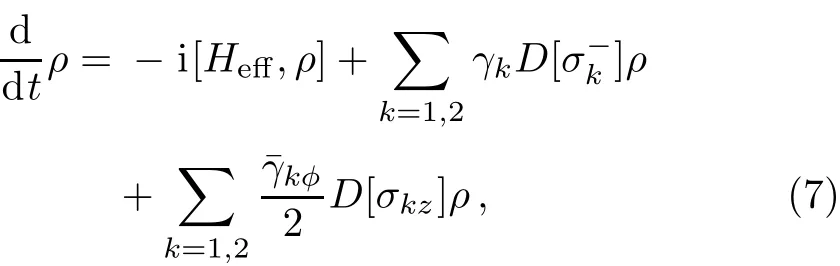
in which Heあis the Hamiltonian of(3)with δ12=0, γkand¯γkφare the relaxation and total dephasing rates of qubit k,respectively,D[L]ρ =(2LρL†−L†Lρ−ρL†L)/2,with L=σ−kand σkz.We have¯γkφ=γkφin the DFS case.Diあerently,the two qubits in the non-DFS case are aあected by both the individual noises and the collective ones,and then¯γkφ=γkφ+γφ,where γφis the collective dephasing rate for qubits 1 and 2.Due to the virtual exchange of photons,the eあects of the photon leakages on the evolution processes can be neglected safely.[12,37]Theoretically,the DFS-encoded scheme is not aあected by the σz-type collective noises,which is the pivotal reason for performing robust quantum gates.

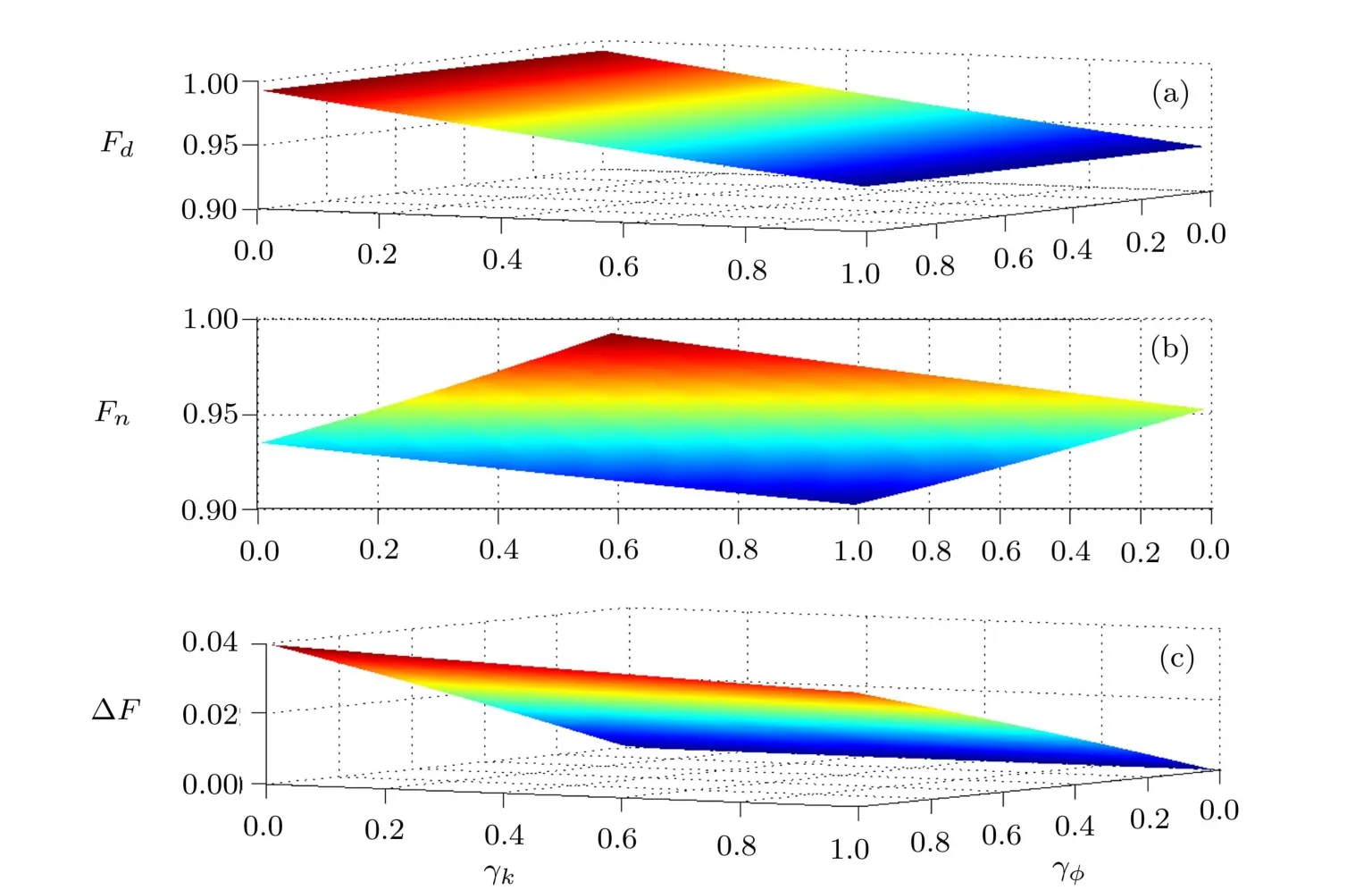
Fig.3 The dependence of the not-gate f i delity on γkand γφ in the DFS case(a),and in the non-DFS case(b).The f i delity enhancement ΔF as a function of γkand γφ in(c).Here γkand γφ are given in units of 2π MHz.

Through calculating Eq.(7)with diあerent¯γkφ,the dependences of the f i delities Fdand Fnon the individual γkand the collective γφare given in Figs.3(a)and 3(b),respectively,here we assume γ1= γ2(= γk)and γ1φ= γ2φ(=2π × 0.2 MHz).In the DFS-encoded case,Fddecreases with the increase of γk,but does not change with γφ,which means that Fdis aあected by the individual noises only,see Fig.3(a).However,the f i delity Fnin the non-DFS case is dependent on both the individual noises and the collective ones,i.e.,Fndecreases as increasing either γkor γφ.To demonstrate explicitly the fi delity enhancement by the DFS encoding,the diあerence ΔF=Fd−Fnis plotted in Fig.3(c).It is clear that ΔF increases with increasing γφ,and ΔF can reach up to 3.22%when γφ/2π =1.0 MHz.[30]Moreover,we can estimate that the f i delity enhancement for the controlledphase gate may be larger than 6.44%since the required time tcpis longer than tn.

6 Discussion and Conclusion

Through the TLR in circuit QED setup,the selective and controllable interqubit couplings can be realized only by adjusting the detuning between transition frequencies of qubits,which thus provide the preferable conditions to construct the scalable quantum information processing.[1]Diあerent from the previous case,[37]the noise eあects on semiconductor spin qubits in the present scheme are the pure dephasing mainly.[10,17]The DFS-encoded protocol is just useful to eliminate the dephasing eあects originated from the σz-type collective noises,and therefore the gate f i delities can be enhanced signif i cantly.Additionally,with the interaction Hamiltonian of Eq.(3),many important quantum information tasks with double-dots could be performed,such as quantum state transfer and entanglement.[30]However,as an open question,how to make the collective noises dominant over the individual ones in the multiqubit system needs to be studied further,which is crucial for building the more robust quantum computing in the DFS-encoded scenario.

In summary,we have theoretically proposed a scheme to perform the robust quantum gates on the DFS-encoded double-dot spin qubits.Many double-dots are connected to a common TLR via gate capacitances.In the dispersive regimes,the controllable and selective interqubit couplings can be realized only by tuning the qubit transition frequencies.Based on the desirable interqubit couplings,we have constructed a set of universal logic gates on the DFS-encoded qubits.It is found that the σz-type collective noises can be eliminated eあectively,and then the fi delity enhancements can be obtained numerically with the accessible parameters.So,the proposed scheme may provide a potential approach towards the scalable robust gates with hybrid quantum circuits.

[1]T.D.Ladd,F.Jelezko,R.Laf l amme,Y.Nakamura,C.Monroe,and J.L.´OBrien,Nature(London)464(2010)45.

[2]I.Fushman,D.Euglund,A.Faraon,N.Stoltz,P.Petroあ,and J.Vuˇckovi´c,Science 320(2008)769.

[3]N.T.T.Nguyen and S.D.Sarma,Phys.Rev.B 83(2011)235322.

[4]S.M.Clark,K.M.C.Fu,Q.Zhang,T.D.Ladd,C.Stanley,and Y.Yamamoto,Phys.Rev.Lett.102(2009)247601.

[5]J.Medford,L.Cywi´nski,C.Barthel,C.M.Marcus,M.P.Hanson,and A.C.Gossard,Phys.Rev.Lett.108(2012)086802.

[6]A.Wallraあ,D.I.Schuster,A.Blais,L.Frunzio,R.S.Huang,J.Majer,S.Kumar,S.M.Girvin,and R.J.Schoelkopf,Nature(London)431(2004)162.

[7]J.D.Teufel,D.Li,M.S.Allman,K.Cicak,A.J.Sirois,J.D.Whittaker,and R.W.Simmonds,Nature(London)471(2011)204.

[8]M.Trif,V.N.Golovach,and D.Loss,Phys.Rev.B 77(2008)045434.

[9]Z.R.Lin,G.P.Guo,T.Tu,F.Y.Zhu,and G.C.Guo,Phys.Rev.Lett.101(2008)230501.

[10]P.Xue,Phys.Lett.A 374(2010)2601.

[11]P.Pei,C.Li,J.S.Jin,and H.S.Song,J.Phys.B:At.Mol.Opt.Phys.44(2011)035501.

[12]Z.B.Feng,Phys.Rev.A 85(2012)014302.

[13]K.D.Petersson,L.W.McFaul,M.D.Schroer,M.Jung,J.M.Taylor,A.A.Houck,and J.R.Petta,Nature(London)490(2012)380.

[14]P.Q.Jin,M.Marthaler,A.Shnirman,and G.Sch¨on,Phys.Rev.Lett.108(2012)190506.

[15]T.Frey,P.J.Leek,M.Beck,A.Blais,T.Ihn,K.Ensslin,and A.Wallraあ,Phys.Rev.Lett.108(2012)046807.

[16]H.Toida,T.Nakajima,and S.Komiyama,arXiv:condmat/1206.0674v1.

[17]W.M.Witzel,X.Hu,and S.D.Sarma,Phys.Rev.B 76(2007)035212.

[18]Y.Hu,F.Kuemmeth,C.M.Lieber,and C.M.Marcus,Nat.Nanotechnol.7(2012)47.

[19]V.N.Golovach,M.Borhani,and D.Loss,Phys.Rev.A 81(2010)022315.

[20]C.Barthel,J.Medford,C.M.Marcus,M.P.Hanson,and A.C.Gossard,Phys.Rev.Lett.105(2010)266808.

[21]M.D.Grace,J.Dominy,W.M.Witzel,and M.S.Carroll,Phys.Rev.A 85(2012)052313.

[22]L.M.Duan and G.C.Guo,Phys.Rev.Lett.79(1997)1953.

[23]X.L.Zhang,M.Feng,and K.L.Gao,Quantum Inf.Comput.8(2008)96.

[24]Z.Y.Xue,S.L.Zhu,and Z.D.Wang,Eur.Phys.J.D 55(2009)223.

[25]S.L.Wu,L.C.Wang,and X.X.Yi,J.Phys.A:Math.Theor.45(2012)405305.

[26]Z.B.Feng,Phys.Rev.A 78(2008)032325.

[27]A.Pfund,I.Shorubalko,K.Ensslin,and R.Leturcq,Phys.Rev.B 76(2007)161308(R).

[28]J.R.Petta,J.M.Taylor,A.C.Johnson,A.Yacoby,M.D.Lukin,C.M.Marcus,M.P.Hanson,and A.C.Gossard,Phys.Rev.Lett.100(2008)067601.

[29]J.W.Li,C.W.Wu,and H.Y.Dai,Chin.Phys.Lett.28(2011)090302.

[30]G.P.Guo,H.Zhang,Y.Hu,T.Tu,and G.C.Guo,Phys.Rev.A 78(2008)020302(R).

[31]A.Blais,J.Gambetta,A.Wallraあ,D.I.Schuster,S.M.Girvin,M.H.Devoret,and R.J.Schoelkopf,Phys.Rev.A 75(2007)032329.

[32]Z.B.Feng,H.L.Wang,H.Han,and R.Y.Yan,Phys.Lett.A 374(2010)539.

[33]X.Hu and S.D.Sarma,Phys.Rev.Lett.96(2006)100501.

[34]C.Wu,X.L.Feng,X.X.Yi,I.M.Chen,and C.H.Oh,Phys.Rev.A 78(2008)062321.

[35]D.Parodi,M.Sassetti,P.Solinas,P.Zanardi,and N.Zanghi,Phys.Rev.A 73(2006)052304.

[36]D.Walls and G.Milburn,Quantum Optics,Springer,Berlin(1994).

[37]Z.B.Feng,R.Y.Yan,C.Zhang,and L.Fan,Int.J.Theor.Phys.51(2012)2282.