Dynamics of Light in Teleparallel Bianchi-Type I Universe

M.Salti

Physics Department,Faculty of Art and Science,Mersin University,Mersin 33342,Turkey

1 Introduction

The Duきn–Kemmer–Petiau(DKP)equation is an eligible relativistic wave equation that describes spin-0 and spin-1 bosons with the advantage over standard relativistic equations.[1]A detailed investigation of DKP equation can be found in Refs.[2–4].Next,Akhiezer and Berestetskii,[5]in 1965,discussed an application of the DKP f i eld to scalar QED.More recently,there have been new interests in DKP theory:it has been applied to QCD by Gribov[6]and to covariant Hamiltonian dynamics by Kanatchikov.[7]On the other hand,it has been studied in curved spacetime,[1]discussed in casual approach[8]and investigated with 5D Galilean covariance.[9]There also have been given detailed proofs of the equivalance between DKP and Klein–Gordon f i elds,[10]and some points regarding DKP interaction with electromagnetic f i eld.[11]

The torsion gravity(or teleparallel gravity)is an alternative approach to gravitation and corresponds to a gauge theory for the translation group based on Weitzenb¨ock geometry.[12]In this theory,gravitation is attributed to torsion,[13]which plays the role of a force,[14]and the curvature tensor vanishes identically.The interesting place of torsion gravity is that,due to its gauge structure,it can reveal a more convenient approach to consider some specif i c problems.

The wave equation for spin-0 and spin-1 bosons in torsion gravity is def i ned as[15]

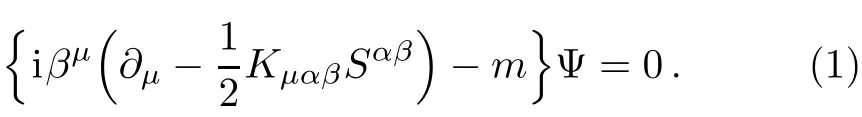
Here Kµαβand Sαβare the torsion tensor and spin tensor,respectively.Next,the β-matrices obey the following algebraic relations

Here a,b,c=0,1,2,3,and ηabis the metric tensor of Minkowski spacetime with signature(+,−,−,−).The Latin alphabet will be used to indicate Minkowski indexes,while Riemann–Cartan indexes will be indicated by Greek letters.

The DKP equation is very similar to Dirac’s equation but the algebraic properties of βamatrices,which have no inverses,make it more diきcult to deal with.These matrices are given by the def i nition:

and they are related to fl at Minkowski spacetime as βµ(x)=hµ(i)β˜(i)with a tetrad frame that satis fi es

In relativistic quantum mechanics,the counterpart of the Maxwell equations can be described by taking zero-mass limit of the DKP equation. Unal,in 1997,showed that the wave equation of massless spin-1 particle in f l at space-time is equivalent to free space Maxwell equations.[16]Then,Unal and Sucu solved the general relativistic massless-DKP(mDKP)equations in Robertson-Walker space-time written in spherical coordinates.[17]By using the same technique,in Einstein’s theory of general relativity,the mDKP equation had been solved for various spacetimes and showed the mDKP equation is equivalent to free space Maxwell equations.[18−21]In the method,the β-matrices are written as a direct product of Pauli spin matrices with unit matrix and this def i nition leads to a spinor which is related to complex combination of the electric and magnetic f i elds.On the other hand,the quantum mechanical solution is important to discuss the wave-particle duality of electromagnetic f i elds,since the particle nature of the electromagnetic f i eld can be analyzed only by a quantum mechanical equation.Furthermore,the mDKP equation removes the unavoidable usage of(3+1)D spacetime splitting formalism for the Maxwell equations.[22]

The mDKP equation in torsion gravity is given as

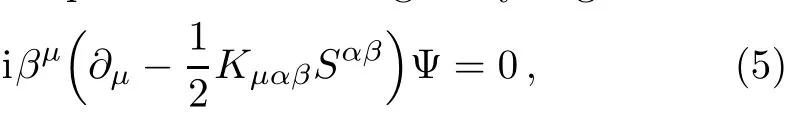
where βµare now:

with σµ=(I,→σ).Next,the spin tensor can be def i ned as

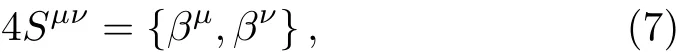
and the torsion tensor is written as

or

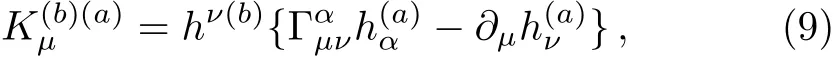
with Christoあel symbols

In the present work,we investigate the behavior of the massless spin-1 particles by examining mDKP equation in the Bianchi-type I universe in teleparallel gravity.The work is organized as follow:in the next section we investigate the mDKP equation in torsion gravity explicitly and obtain its second order form for a given geometry.In Sec.3,we discuss the free-space Maxwell equations the Bianchi-type I universe.In Sec.4,we f i nd oscillating frequency of the photon.Finally,we discuss our results.

2 Massless Spin-1 Particles in Torsion Gravity

The line-element of the Bianchi-type I universe is

where A,B,and C are functions of t alone and these expansion factors could be determined via f i eld equations in Einstein’s theory of general relativity or torsion gravity.We know that the non-trivial tetrad f i eld induces a torsion gravity structure on spacetime,which is directly related to the presence of the gravitational f i eld.Using the relation(4),we obtain the tetrad components:

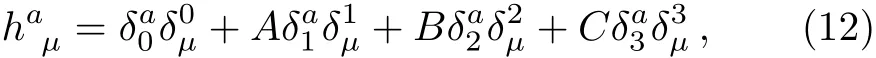
and its inverse is

The line-element given by Eq.(11)can be reduced to the fl at Friedmann–Robertson-Walker line element in a special case.De fi ning A=B=C=T(t)and transforming the line-element(11)from t,x,y,z coordinates to the spherical coordinates,we obtain

according to:

The Friedmann-Robertson-Walker spacetime has received considerable interests in the relativistic cosmology.Maybe one of the most important features of this model is,as predicted by inf l ation,[23−25]the f l atness which agrees with the observed cosmic microwave background radiation.

By using the def i nition of Christoあel symbols given by Eq.(10),the non-vanishing components are found as

where a dot indicates the derivative with respect to t.Thence,the surviving components of the torsion tensor are obtained as

or in another form we f i nd

By making use of Eq.(6)we get

Now,we obtain the mDKP equation as:

where

Then,Eq.(29)can be re-written as

Next,after using the standard representation of Pauli spin matrices,and def i ning the 4-component wave-function as

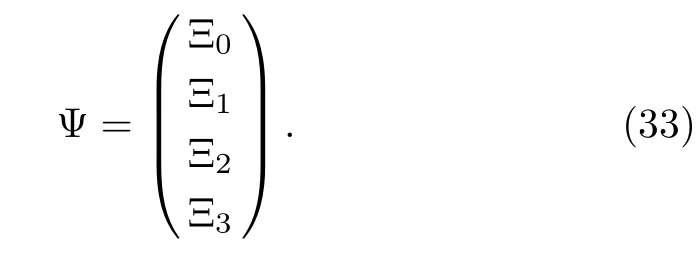
Equation(32)gives the following equations

Here,one can see that we have Ξ1= Ξ2.Then,by making use of this relation,we f i nd

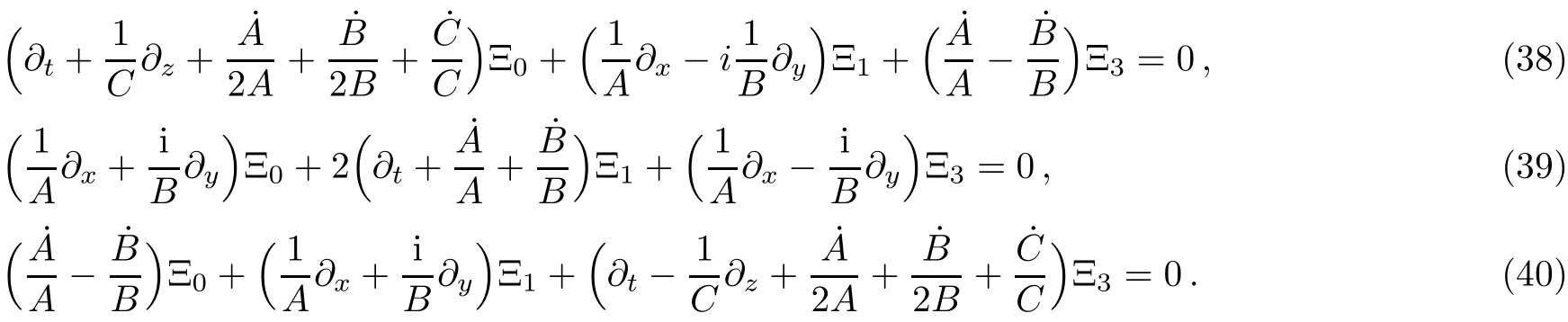
After def i ning the following new wave functions

Equations(38),(39),and(40)transform into another forms:

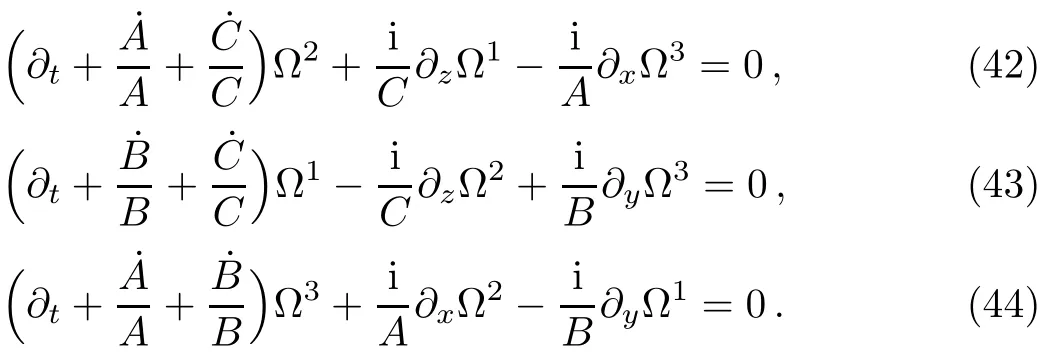
After this step,now we perform the following Fourier transformation,

where m=1,2,3.Hence,we f i nd

By def i ning

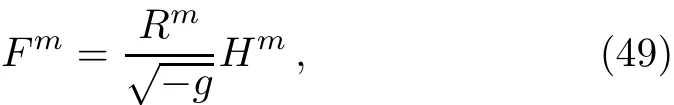
with R1=A,R2=B,and R3=C,we get

We can write these equations in a general form[26]

To solve th

is equation exactly,for suitable symmetry,we can use spherical coordinates.From this point of view,Hmshould be written in terms of spherical coordinates.The components of k in spherical coordinates are def i ned as

k1=k sinθ cosϕ, k2=ksinθsinϕ, k3=k cosθ,(54)or in matrix representations

where

On the other hand,we def i ne also

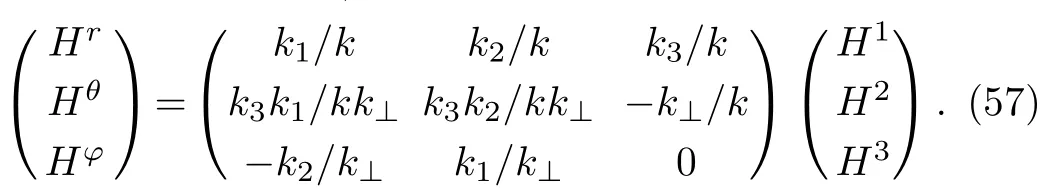
Ergo we have

and we obtain

where

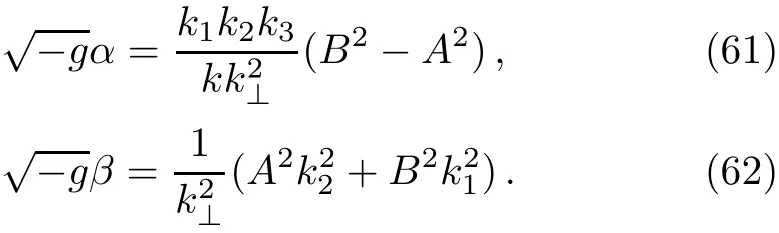
Here the parameter γ is determined by

with

Λ2is a generalization of the dispersion relation ω2=|k|2.After eliminating Hϕfrom Eqs.(59)and(60),we obtain the following second order diあerential equation:

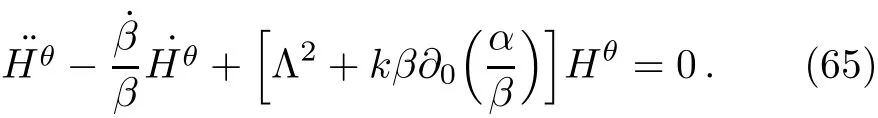
In an explicit form,this result can be re-written as

We mentioned before that if we def i ne

theBianchi-typeImodeltransformsinto thef l at Friedmann-Robertson-Walker spacetime.Hence,under this limit,Eq.(66)is reduced to

Now,by def i ning conformal time as

we get

It is easy to see that this equation has the following solution,

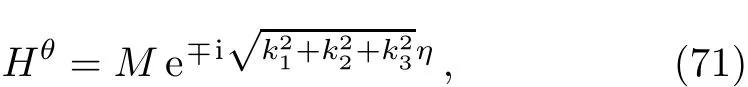
where M is a normalization constant.

3 Free-Space Maxwell Equations in the Bianchi-type I Universe

The interaction of electromagnetic and gravitational fi elds is described by the Maxwell equations in a given background and source.In the absence of an electromagnetic source these equations are written as

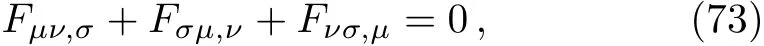
where Fµν= ∂µAν− ∂νAµ. Here we investigate the Maxwell equations for the line-element given by Eq.(11)to show the correspondence between the mDKP equation in torsion gravity and the Maxwell equations.The covariant and covariant f i eld strengths,Fµνand Fµν,in the general coordinates are

where E(i)and B(i)are the components of the electric and magnetic f i elds in the local Lorentz frame.In terms of these components,Maxwell equations can be expanded as

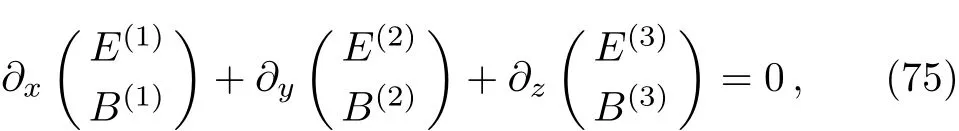
By def i ning a complex spinor Ξ:

and making a suitable Fourier transformation:

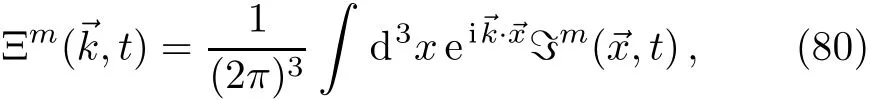
for the spinor form of the Maxwell equations we f i nd

To eliminate˙A/A+˙C/C,˙B/B+˙C/C,and˙A/A+˙B/B terms,we can def i ne:

with R1=A,R2=B,and R3=C.Thence,we get

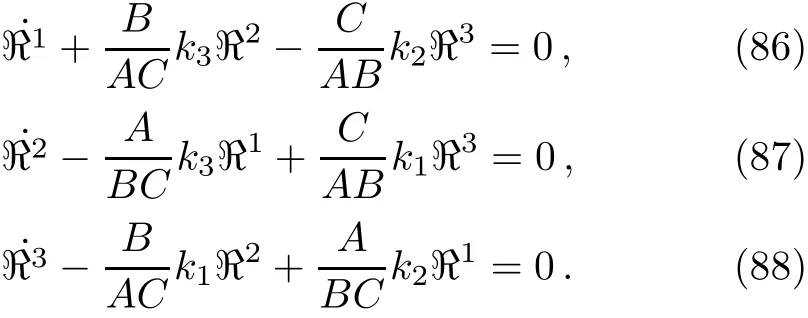
These three equations are exactly the same results as obtained torsion gravity(see Eqs.(50),(51),and(52)).

4 Oscillation Region

A general method to f i nd the frequency spectrum is to impose the condition on functions,which are the solutions of diあerential equation.The functions must be bounded for all values as usually done in quantum mechanics,this procedure gives the quantization of frequency.Since we did not solve the mDKP equation exactly,we will restrict ourselves to discuss how we can obtain the oscillation region of the photon.

The general method for obtaining the oscillation region is to write the diあerential equation that does not include the f i rst derivative and simulate this to the second order diあerential equation that describes the harmonic oscillator.Here we def i ne

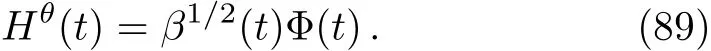
Next,by making use of this def i nition in Eq.(65),we obtain

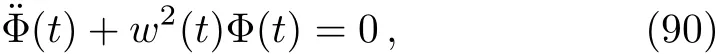
where

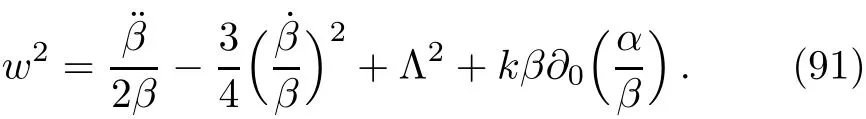
Hence the oscillation region is:

5 Conclusions

In this work we mainly focused on the Duきn–Kemmer–Petiau theory in torsion gravity for the generalized Bianchi-type I universe.We have obtained a second order relativistic wave-equation that describes massless spin-1 particles coupled to the gravitational f i eld.The method of separation of variables and the Fourier transformation has been used due to the symmetry of the generalized Bianchi-type I spacetime.Also,the oscillatory behavior of the result has been discussed.Furthermore,we show that the massless Duきn–Kemmer–Petiau equation in torsion gravity and the free-space Maxwell equations agree with each other and give the same results.This interesting feature strongly motivates us to use the massless Duきn–Kemmer–Petiau equation in torsion gravity to investigate the dynamics of light.Another motivation is that the results obtained can be used to discuss the Photon production in some special spacetime models.

[1]J.T.Lunardi,B.M.Pimentel,and R.G.Teixeria,Geometrical Aspect of Quantum Fields:Proc.(2000)Londrina Workshop(Londrina,Brazil)eds.A.A.Bytsenko,A.E.Golcaves,and B.M.Pimentel,World Scientif i c,Singapore(2001)p.111.

[2]G.Petiau,University of Paris Thesis(1936),Published in Acad.Roy.de Belg.,Classe Sci.Mem in 8o 16,No.2(1936).

[3]R.J.Duきn,Phys.Rev.54(1938)1114.

[4]N.Kemmer,Proc.Roy.Soc.A 173(1939)91.

[5]A.I.Akhiezer and V.B.Berestetskii,Quantum Electrodynamics,Interscience,New York(1965).

[6]V.Gribov,Eur.Phys.J.C 10(1999)71.

[7]I.V.Kanatchikov,Rep.Math.Phys.46(2000)107.

[8]J.T.Lunardi,L.A.Manzoni,B.M.Pimentel,and J.S.Valverde,Int.J.Mod.Phys.A 17(2002)205.

[9]M.de Montigny,F.C.Khanna,A.E.Santana,E.S.Santos,and J.D.M.Vienna,J.Phys.A 33(2000)L273.

[10]V.Ya Fainberg and B.M.Pimentel,Theor.Math.Phys.124(2000)1234;Phys.Lett.A 271(2000)16;Braz.J.Phys.30(2000)275.

[11]M.Nowakawski,Phys.Lett.244(1998)329.

[12]R.Weitzenb¨ock,Invarianttent theorie,Gronningen,Noordhoあ(1923).

[13]K.Hayashi and T.Shirafuji,Phys.Rev.D 19(1978)3524.[14]V.V.de Andrade and J.G.Pereira,Phys.Rev.D 56(1997)4689.

[15]J.T.Lunardi,B.M.Pimentel,and R.G.Teixeira,Gen.Rel.Grav.34(2002)491.

[16]N.Unal,Found.Phys.27(1997)795.

[17]N.Unal and Y.Sucu,Int.J.Mod.Phys.A 17(2002)1137.

[18]A.Havare and T.Yetkin,Class.Quant.Grav.19(2002)2783;Chin.J.Phys.41(2003)475.

[19]A.Havare,O.Aydogdu,and T.Yetkin,Int.J.Mod.Phys.D 5(2004)935.

[20]M.Salti and A.Havare,Mod.Phys.Lett.A 20(2005)451.

[21]A.Havare,M.Korunur,O.Aydogdu,M.Salti,and T.Yetkin,Int.J.Mod.Phys.D 14(2005)957.

[22]R.X.Saibabalov,Gen.Rel.Gravit.27(1995)697.

[23]A.H.Guth,Phys.Rev.D 23(1981)347.

[24]A.D.Linde,Phys.Lett.B 108(1982)389;A.D.Linde,Phys.Lett.B 129(1983)177.

[25]A.Albrecht and P.J.Steinhardt,Phys.Rev.D 48(1982)1220.

[26]K.H.Lotze,Class.Quantum Grav.7(1990)2145.