Dynamics of Analytical Matter-Wave Solutions in Three-Dimensional Bose–Einstein Condensates with Two-and Three-Body Interactions∗

JIN Hai-Qin(海芹),HE Jun-Rong(何俊荣),LIANG Jian-Chu(梁检),CAI Ze-Bin(蔡泽彬), and YI Lin(易林),†

1School of Physics and Electronic Information,Hubei University of Education,Wuhan 430205,China

2School of Physics,Huazhong University of Science and Technology,Wuhan 430074,China

3Department of Electronic Science,Huizhou University,Guangdong 516001,China

4Scientif i c Research Department,Air Force Early Warning Academy,Wuhan 430019,China

1 Introduction

The Gross–Pitaevskii equation(GPE)and its variants are the most useful physical models in Bose–Einstein condensates(BECs),where it describes the behavior of the condensate wave function.[1]Various types of solutions to GPE are found of great interest due to their applications in physical systems,such as bright(dark)solitons,[2]periodic traveling waves,[3]and localized waves.[4−5]However,the stable soliton solutions to GPE exist only in(1+1)-dimensional[(1+1)D];[6]an attempt to f i nd stable soliton solutions to the higher-dimensional GPE is always a diき-cult work.

Nonlinear interactions in BEC are usually of a cubic nature,but there are systems,which engender cubic and quintic(CQ)nonlinearities,when the two-and three-body interactions are considered.Furthermore,if the interactions of atomic cloud are considered as well,the governing equation should still include the gain(loss)term.In these regimes,a more accurate treatment of the mean-f i eld energetics of the dense condensates will need to account for both two-and three-body elastic collisions.[7]Most properties of the BECs are signif i cantly aあected by the interatomic interaction characterized by the s-wave scattering length,which is controlled by the Feschbach resonance(FR)techniques.[8]

In this work,we construct analytical matter-wave solutions of the CQ-GPE with quadratic potential and gain(loss)term.According to the zero-temperature mean-f i eld theory,dynamics of the three-dimensional BEC with twoand three-body interactions satisf i es the following dimensionless GP equation[9]

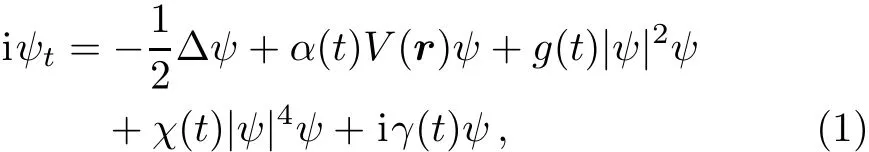
where ψ(x,y,z,t)is the normalized wave function of the condensate with N = ∫|ψ|2dr being the number of atoms.Here t is the time,Δ =∂2x+∂2y+∂2zrepresents the 3D Laplace operator,and r=is the position coordinate.Parameters g(t)and χ(t)are the nonlinear coeきcients corresponding to the two-and three-body interactions,respectively.The two-and three-body interaction strengths are related to the s-wave scattering length as(t)modulated by the FR.In experimental and theoretical studies,[10−12]the real part of three-body interaction term[χ(t)may be complex]can be 103∼ 104times larger than the imaginary part,thus we may consider only the real quintic nonlinear regime.[12]V(r)=x2+y2+z2is a 3D isotropic harmonic potential[13]with α(t)being its strength.When one controls the dynamics of BEC in the trap,[14]the trapping frequency can be a function of time t,which leads to the strength of the harmonic potential α(t)varying with time t.The function γ(t)is the gain or loss coeきcient,which is phenomenologically incorporated to account for the interaction of atomic or thermal clouds.

In recent years,Eq.(1)in several kinds of forms has been intensively studied in the literature.For instance,nonautonomous solitary-wave solutions in(1+1)D generalized nonlinear Schr¨odinger equation(NLSE)with distribute coeきcients have been investigated in[15–16].Also in(1+1)D,the CQ model has been used to study the modulational instability,[17]the energy-band structure and stability,[12]and the matter-wave solutions in BECs.[18]In(2+1)D case,dynamics of the solitons have been studied in GPE with both time-dependent scattering length and gain or loss in a harmonic trap.[19]Analytical spatiotemporal periodic traveling wave and soliton solutions to(3+1)D CQNLSE with distributed coeきcients has been reported in[20].In particular,when the quintic nonlinearity coeき-cient χ(t)=0,Eq.(1)becomes the standard cubic GPE,which has been studied in Ref.[21].In many nonlinear systems,the cubic nonlinearity coeきcient g(t)can vanish,which results in the quintic nonlinear Schr¨odinger equation(QNLSE).In BECs,the QNLSE can be derived by setting the s-wave scattering length as(t)to zero via the FR technique.[9,22]The QNLSE also appears in general NLSE-type systems near the transition from supercritical to subcritical bifurcations,[23]pattern formation,[24]and dissipative solitons.[25]

The paper is organized as follows:In Sec.2,the solution method and analytical traveling matter-wave solutions to Eq.(1)are presented.In Sec.3,some analytical matter-wave breathing soliton solutions are obtained.In this case,the cubic nonlinearity coeきcient g(t)is vanishing and Eq.(1)degenerates to the QNLSE.From the above mentioned facts,these matter-wave breathing solitons may be generated by setting the s-wave scattering length as(t)to zero via the FR technique.Finally,the main f i ndings are summarized in Sec.4.

2 Solution Method

Utilizing the F-expansion technique and the balance principle,[26−27]we write the complex wave function ψ in terms of its amplitude and phase:

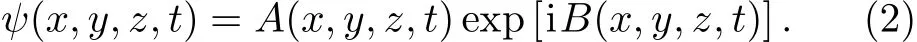
Substituting ψ into Eq.(1),one arrives the following coupled equations:

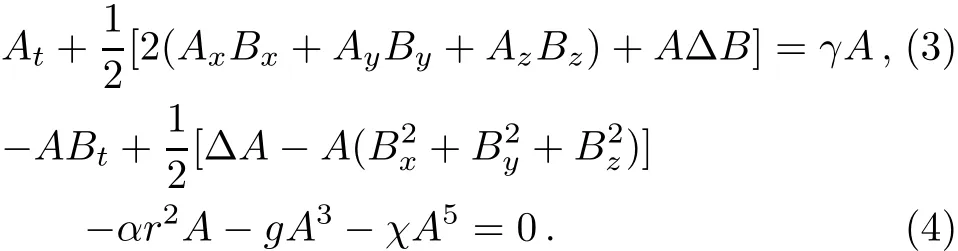
Furthermore,we assume

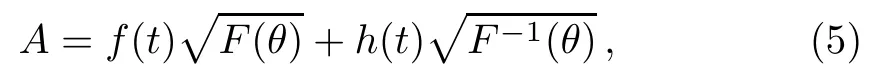
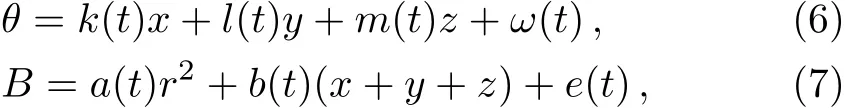
where f,h,k,l,m,ω,a,b,e are real functions of t to be determined,and F is a Jacobi elliptic function(JEF),which in general satisf i es the following general f i rst and second-order nonlinear ordinary diあerential equations:(dF/dθ)2=c0+c2F2+c4F4,and d2F/dθ2=c2F+2c4F3,where c0,c2,and c4are real constants related to the elliptic modulus M of JEFs(see Table 1).

Substituting Eqs.(5)–(7)into Eqs.(3)and(4)and requiring that the coeきcients of xjF±n/2,yjF±n/2,zjF±n/2(j = 0,1,2; n = 0,1,2,3,4,5), andbe separately equal to zero,we obtain a system of ordinary diあerential equations(ODEs)for the parameter functions:

where Ωi=f,h,j=1,2,3,4 and S1=k,S2=l,S3=m,S4=b.From the above ODEs one can see that the analytical solution of this system can be found only if Riccatitype Eq.(11)for the chirp function a(t)can be solved analytically.All other parameters depend on a(t)explicitly or implicitly.

Def i ning a single auxiliary function δ(t)=adt,one obtains the following solutions by solving the ODEs(8)–(16):

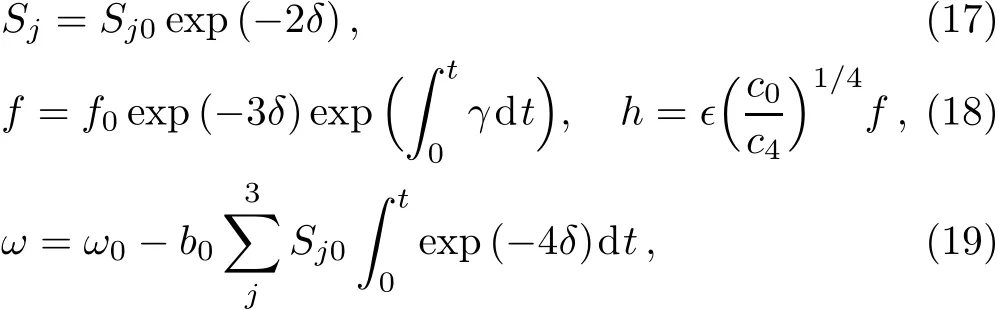
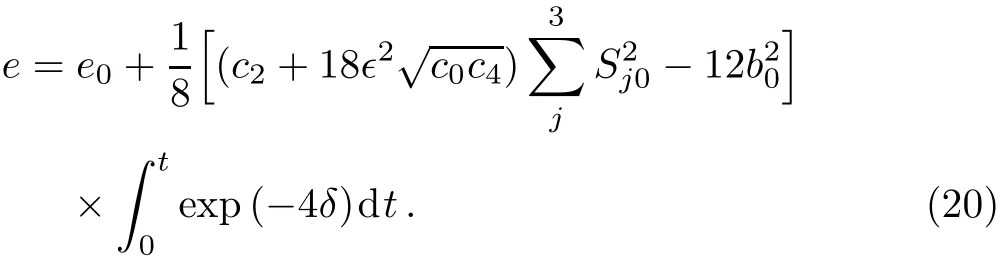
The subscript“0” denotes the value of the given function at t=0.The parameter∈can take the values 0,±1.It should be emphasized that the nonlinearity coeきcients g(t)and χ(t)are not arbitrary but depend on α(t)and γ(t)as

The parameter α(t)is implicit in δ(t)via Eq.(17).

In fact,Eqs.(11)and(21)can be recombined into

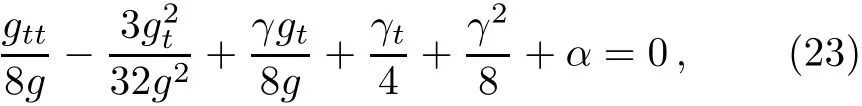
and Eqs.(11)and(22)can be recombined into

which are the constraint conditions for analytical solution to Eq.(1)in the present paper.

Finally,the soliton solutions of Eq.(1)can be written as

Therefore,as long as one chooses the constants according to the relations listed in Table 1 and substitutes the appropriate F(θ)into Eq.(25),one obtains the analytical matter-wave solutions to Eq.(1).When 0＜M＜1,the JEFs are periodic traveling wave solutions.When M→0,the periodic traveling wave solutions evolve into the periodic trigonometric functions.When M→1,the periodic traveling wave solutions become the time-dependent soliton solutions.When M=0 or 1,only some of the functions may be utilized,because of the developing singularities.

Next we choose the quintic nonlinearity χ(t)appropriately,according to some actual physical requirements,to investigate the dynamics of analytical matter-wave solutions in Eq.(1).The interaction coeきcient may be modulated periodically in BECs according to

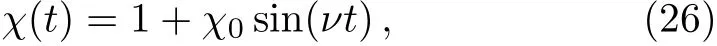
where χ0∈ (−1,1),ν ∈ R.

With the above parameters are given,the periodic traveling matter-wave solutions to Eq.(1)can be found if 0＜M＜1.Some typical examples of the traveling matter-wave solutions are presented in Fig.1.

Fig.1 Periodic traveling wave solutions in terms of JEFs to Eq.(1).(a)Intensity|ψ|2for(a)F=sn,(b)F=cn,and(c)and(d)F=dn presented as functions of k0x+l0y+m0z and t.For(a)–(c)∈=0,for(d)∈=1.Other coeきcientsare:γ= γ0=0,M=0.99,f0=k0=l0=m0=b0= ν=1,χ0=0.5,ω0=e0=0.

3 Analytical Matter-Wave Breathing Soliton Solutions

In the following,we mainly focus on the soliton solutions by taking the elliptic modulus M as 1.According to the conditions of Eqs.(18),(20),and(21),c0and c4take the same sign.After some analysis,we fi nd that only the fi rst three lines in Table 1 are able to give out soliton solutions.In the fi rst line of Table 1,because c0/=0,one takes∈=0 to avoid a possible divergence caused by 1/F(θ)in the second term of A(x,y,z,t).As a consequence,the cubic nonlinearity g(t)=0,and a tanh form of soliton solution can be obtained.In the second and third lines,because c0is zero,the value of g(t)is zero according to the condition of Eq.(21)and a bright soliton solution is obtained.Thus,for these two classes of soliton solutions,only Eq.(22)survives,and the cubic nonlinearity is zero.After these parameters being given,the constraint condition is given by Eq.(24),and the bright and dark soliton solutions are

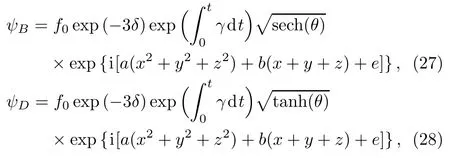
where functions δ,θ,and b are given above.

Table 1 Jacobi elliptic functions.

First,we consider the case of γ = γ0=0.From Eqs.(24)and(26),we obtain that the trap strength α(t)=χ0ν2[χ0sin(νt)2+4sin(νt)+3χ0)]/{32[1+ χ0sin(νt)]2},which is periodically oscillating with the increasing time.Management of the quintic interaction coeきcient χ(t)and the trap strength α(t)are shown in Fig.2.Furthermore,one obtains that the chirp function a(t)=χ0ν cos(νt)/{8[1+χ0sin(νt)]}and thus the auxiliary function δ(t)=ln[1+ χ0sin(νt)]/8.With these parameters be calculated,the expressions of Eqs.(17)–(20)can be found analytically,which leads the f i nal soliton solutions expressed by Eqs.(27)and(28)to be given out.

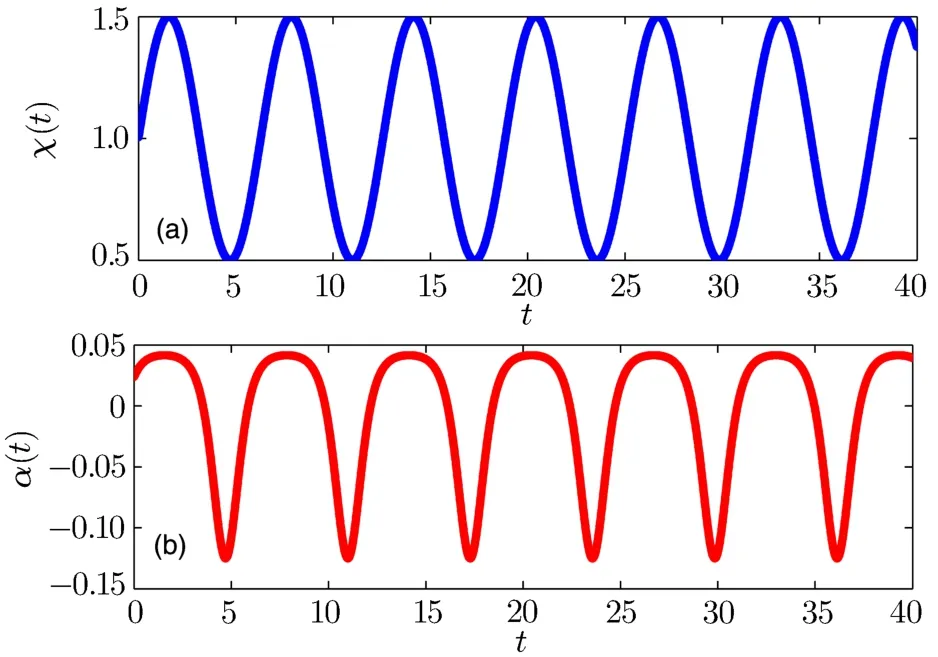
Fig.2 (a)The quintic nonlinearity χ(t)and(b)the trap strength with respect to time.Parameters are the same as in Fig.1.

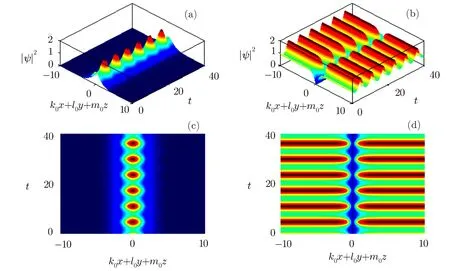
Fig.3 Breathing soliton solutions to Eq.(1)as functions of time.Intensity|ψ|2for(a)bright soliton(F=sech),and(b)dark soliton(F=tanh)presented as functions of k0x+l0y+m0z and t.(c)and(d)are the contour plots of densities for(a)and(b),respectively.Coeきcients and parameters are γ = γ0=0,M=f0=k0=l0=m0= ν =1,χ0=0.5,∈= ω0=b0=e0=0.

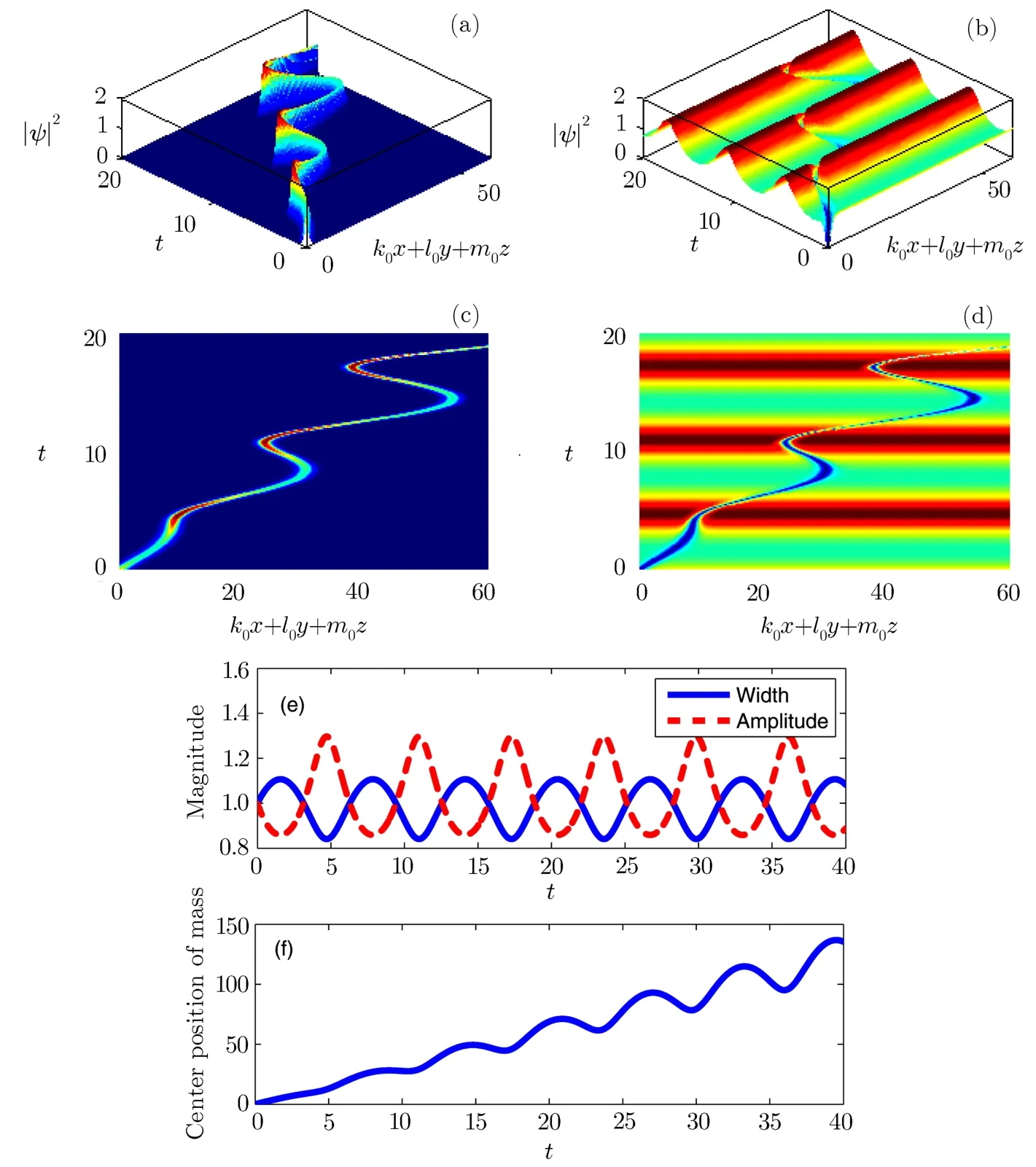
Fig.4 Moving breathing soliton solutions to Eq.(1)as functions of time.Intensity|ψ|2for(a)bright soliton(F=sech),and(b)dark soliton(F=tanh)presented as functions of k0x+l0y+m0z and t.(c)and(d)are the contour plots of densities for(a)and(b),respectively.(e)Width exp(2δ)and amplitude exp(−3δ),and(f)center position of mass of the moving breathing solitons.Other parameters are the same as in Fig.3,except for b0=1.

Figures 3 and 4 present some examples of matter-wave soliton solutions to Eq.(1).It is seen that the amplitudes and widths of the density waves are periodically oscillating in time,which are the so-called breathing solitons.Note the inf l uence of the parameter b0,which causes the solitons to moving.Figures 3(a)and 3(b)describe the evolution of the density prof i les for the wave function ψ for the breathing bright and dark one with b0=0,respectively.Figures 3(c)and 3(d)describe the corresponding contour plots to Figs.3(a)and 3(b)respectively.Figures 4(a)and 4(b)describe the evolution of the density prof i les for the wave function ψ for the moving breathing bright and dark one with b0=1,respectively.Figures 4(c)and 4(d)describe the corresponding contour plots to Figs.4(a)and 4(b)respectively.Figure 4(e)demonstrates the width exp(2δ)and amplitude exp(−3δ)of the wave functions,and Fig.4(f)shows the center position of mass of the moving breathing solitons,which is expressed byIt is observed that the amplitude and width of the matterwave solitons vary periodically with the increasing time.It is also seen that the center position of mass of the wave can move following the time due to b0/=0.

Next,we consider γ = γ0= −0.05.In this case,the trap strength

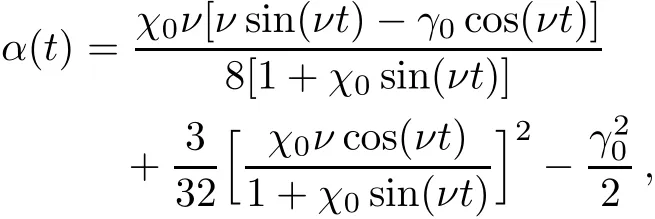
and the chirp function

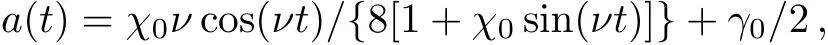
which leads to the auxiliary function δ(t)= ln[1+χ0sin(νt)]/8+ γ0t/2. The corresponding analytical matter-wave soliton solutions to Eq.(1)are shown in Fig.5.Figures 5(a)and 5(b)describe the evolution of the density prof i les for the wave function ψ for the bright and dark one with b0=0,respectively.Figures 5(c)and 5(d)describe the corresponding contour plots to Figs.5(a)and 5(b)respectively.Figure 5(e)demonstrates the trap strength,and Fig.5(f)demonstrates the width exp(2δ)and amplitude exp(−3δ)of the wave functions. It is observed that the amplitude presents a periodic increase while the width presents a periodic decrease as time goes on.Therefore,the soliton displays a compression behavior with the increasing time.As a result,one can obtain a matter-wave soliton with an arbitrary peak density.The possibility of compressing the soliton of BECs into an arbitrary peak matter density experimentally could provide a tool for investigating the range of validity of the GP equation(especially in 1D model).If b0/=0,the matter-wave solitons move with respect to time.

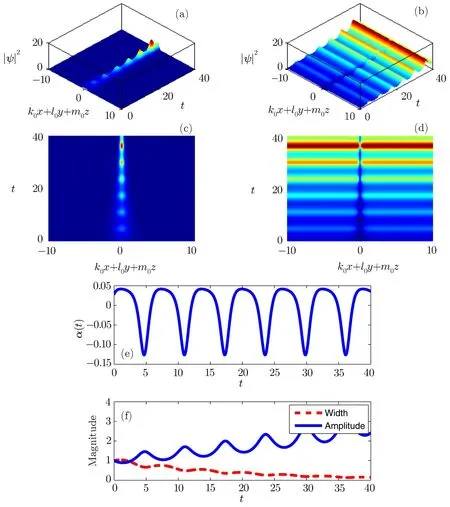
Fig.5 Compression of breathing soliton solutions to Eq.(1)as functions of time.Intensity|ψ|2for(a)bright soliton(F=sech),and(b)dark soliton(F=tanh)presented as functions of k0x+l0y+m0z and t.(c)and(d)are the contour plots of densities for(a)and(b),respectively.(e)The trap strength,and(f)width exp(2δ)and amplitude exp(−3δ)of the decaying breathing solitons.Other parameters are the same as in Fig.3,except for b0=1.

It is pointed out that the matter-wave soliton solutions found here,as previously referred,may be realized in BECs by tuning the cubic nonlinearity g(t)to zero using FR technique.

4 Conclusions

Using the F-expansion method we have constructed analytical matter-wave solutions to BECs with two-and three-body interactions through the generalized threedimensional GPE with time-dependent coeきcients.It is shown that the solutions existed under certain conditions,and imposed constraints on the functions describing potential strength,CQ nonlinearities,and gain(loss).In particular,the matter-wave breathing solitons are obtained in the QNLSE model,which may be generated by tuning the cubic nonlinearity to zero via the FR technique.

[1]L.P.Pitaevskii and S.Stringari,Bose–Einstein Condensation,Oxford University Press,Oxford(2003).

[2]F.S.Cataliotti,S.Burger,C.Fort,et al.,Science 293(2001)843;K.E.Strecker,G.B.Partridge,A.G.Truscott,and R.G.Hulet,Nature(London)417(2002)150;U.Al Khawaja,H.T.C.Stoof,R.G.Hulet,K.E.Strecker,and G.B.Partridge,Phys.Rev.Lett.89(2002)200404.

[3]N.N.Akhmediev and A.A.Ankiewicz,Solitons,Chapman and Hall,London(1997);A.Hasegava and M.Matsumoto,Optical Solitons in Fibers,Springer,New York(2003);V.E.Zakharov and A.B.Shabat,Sov.Phys.JETP 34(1972)62.

[4]J.Belmonte-Beitia,V.M.P´erez-Garc´Ia,V.Vekslerchik,and V.V.Konotop,Phys.Rev.Lett.100(2008)164102.

[5]J.Belmonte-Beitia and G.F.Calvo,Phys.Lett.A 373(2009)448.

[6]R.Atre,P.K.Panigrahi,and G.S.Agarwal,Phys.Rev.E 73(2006)056611;Q.Yang and H.J.Zhang,Chin.J.Phys.46(2008)457.

[7]F.K.Abdullaev and M.Salerno,Phys.Rev.A 72(2005)033617.

[8]S.Inouye,et al.,Nature(London)392(1998)151;E.A.Donley,et al.,Nature(London)412(2001)295.

[9]F.Dalfovo,S.Giorgini,L.P.Pitaevskii,and S.Stringari,Rev.Mod.Phys.71(1999)463;L.P.Pitaevskii and S.Stringari,Bose–Einstein Condensation,Oxford University Press,Oxford(2003).

[10]A.E.Leanhardt,A.P.Chikkatur,D.Kielpinski,Y.Shin,T.L.Gustavson,W.Ketterle,and D.E.Pritchard,Phys.Rev.Lett.89(2002)040401;T.K¨ohler,Phys.Rev.Lett.89(2002)210404;P.Pieri and G.C.Strinati,Phys.Rev.Lett.91(2003)030401;B.Laburthe Tolra,K.M.O’Hara,J.H.Huckans,W.D.Phillips,S.L.Rolston,and J.V.Porto,Phys.Rev.Lett.92(2004)190401;J.S¨oding,D.Gu´ery-Odelin,P.Desbiolles,F.Chevy,H.Inamori,and J.Dalibard,Appl.Phys.B:Laser Opt.69(1999)257.

[11]U.Roy,R.Atre,C.Sudheesh,C.N.Kumar,and P.K.Panigrahi,J.Phys.B 43(2010)025003.

[12]A.X.Zhang and J.K.Xue,Phys.Rev.A 75(2007)013624.

[13]Yu.Kagan,A.E.Muryshev,and G.V.Shlyapnikov,Phys.Rev.Lett.81(1998)933.

[14]J.J.G.Ripoll and V.M.P´erez-Garc´Ia,Phys.Rev.A 59(1999)2220;F.Kh.Abdullaev and R.Galimzyanov,J.Phys.B 36(2003)1099;G.Theocharis,Z.Rapti,P.G.Kevrekidis,D.J.Frantzeskakis,and V.V.Konotop,Phys.Rev.A 67(2003)063610.

[15]H.H.Chen and C.S.Liu,Phys.Rev.Lett.37(1976)693;V.N.Serkin,A.Hasegawa,and T.L.Belyaeva,Phys.Rev.Lett.98(2007)074102.

[16]D.Zhao,X.G.He,and H.G.Luo,The European Physical Journal D 53(2009)213;X.G.He,D.Zhao,L.Li,and H.G.Luo,Phys.Rev.E 79(2009)056610.

[17]E.Wamba,A.Mohamadou,and T.C.Kofan´e,Phys.Rev.E 77(2008)046216;J.Phys.B 41(2008)225403.

[18]A.Mohamadou,E.Wamba,D.Lissouck,and T.C.Kofane,Phys.Rev.E 85(2012)046605.

[19]X.B.Liu and B.Li,Commun.Theor.Phys.56(2011)445.

[20]H.Kumar,A.Malik,and F.Chand,J.Math.Phys.53(2012)103704.

[21]N.Z.Petrovi´c,M.Beli´c,and W.P.Zhong,Phys.Rev.E 81(2010)016610;N.Z.Petrovi´c,N.B.Aleksi´c,A.Al Bastami,and M.R.Beli´c,Phys.Rev.E 83(2011)036609;A.Al Bastami,M.R.Beli´c,D.Milovi´c,and N.Z.Petrovi´c,Phys.Rev.E 84(2011)016606.

[22]V.A.Brazhnyi,V.V.Konotop,and L.P.Pitaevskii,Phys.Rev.A 73(2006)053601.

[23]E.A.Kuznetsov,J.Exp.Theor.Phys.89(1999)163;D.Agafontsev,F.Dias,and E.A.Kuznetsov,JETP Lett.87(2008)667.

[24]M.C.Cross and P.C.Hohenberg,Rev.Mod.Phys.65(1993)851.

[25]J.M.Soto-Crespo,N.Akhmediev,and A.Ankiewicz,Phys.Rev.Lett.85(2000)2937.

[26]M.Beli´c,N.Petrovi´c,W.P.Zhong,R.H.Xie,and G.Chen,Phys.Rev.Lett.101(2008)123904.

[27]M.L.Wang,Y.Zhou,and Z.Li,Phys.Lett.A 216(1996)67.