Dynamic Structure Factor of an Optically Trapped Dipolar Bose–Einstein Condensate∗

QI Wei(漆伟),LIANG Zhao-Xin(梁兆伟), and ZHANG Zhi-Dong(张志东)

Shenyang National Laboratory for Materials Science,Institute of Metal Research,Chinese Academy of Sciences,72 Wenhua Road,Shenyang 110016,China

1 Introduction

Recently,two experiments[1−2]have been reported that they have successfully applied the technique of Bragg spectroscopy in measuring the excitation spectrums of Bose–Einstein condensates(BEC)with long-range interactions. This marks an exciting progress in exploring the intriguing many-body physics of the novel ultra-cold atomic systems with long-range interactions,[3−4]in particular,providing crucial information on the role of the long-range interactions in quantum degenerate gases.

When one compares the two experiments in Refs.[1]and[2],two major diあerences are manifest.First,the former generates a cavity-mediated long-range interaction,which originates from the radiative coupling between the electric dipoles induced by an oあ-resonant laser light;while the latter creates a dipolar BEC with intrinsic dipole-dipole interactions.Second,the Bose gas in Ref.[1]was loaded in an optical lattice,compared to the latticefree geometry in Ref.[2].These comparisons naturally motivate an interesting question that concerns marrying a dipolar BEC and the lattice geometry in the same experiment and using the Bragg spectroscopy to measure the excitation spectrum.[5]Investigations along this direction would be particularly appealing.For one thing,there have been considerable interest recently in exploring the intriguing features and novel phases in the quantum degenerate dipolar gases.For another,the application of the Bragg spectroscopy in the area of cold atoms is itself worth more eあorts.

From the theoretical viewpoints,the technique of Bragg spectroscopy to measure the energy spectrum essentially boils down to probing the dynamic structure factor,namely the response of a BEC to an external density perturbation. As in Refs.[1–2],an atomic BEC is illuminated by two laser beams with a wave vector diあerence q=k1− k2and a frequency diあerence ω that is much smaller than their detuning from an atomic resonance.[6]The two beams then create a periodic traveling intensity modulation Imod(r,t)=I cos(q·r−ωt)which,when coupled to the BEC,generates a perturbation potential Vmod=(V/2)[ρ†qe−iωt+ ρ−qe+iωt]with ρq=∑being the Fourier transformed onebody density operator. The associated response function,namely the dynamical structure factor,[7−8]takes the forms S(q,ω)=(V2/4Nħω2R)∑f|〈f|ρ†q|g〉|2δ(ħω −(Ef−Eg)),with the ground(excited)states|g〉(|f〉)having the energy Eg(Ef)and ωR=V/2ħ being the twophoton Rabi frequency.The dynamic structure factor reveals crucial information on the roles of interatomic interactions and many-body eあects.So far,the eあects of optical lattice and hard-core interactions on the dynamic structure factor[9−11]have been investigated,both theoretically[12−13]and experimentally.[14−15]

The main purpose of this work is to theoretically investigate the dynamical structure factor of a dipolar BEC trapped in a one-dimensional(1D)optical lattice,within the frameworkof Bogoliubov approach.Our results show that,compared to the non-dipolar counterpart,the long-range anisotropic dipole-dipole interaction can significantly aあect the structure of the Bogoliubov bands of the system,particularly the lowest band.Consequently,the dynamic structure factor of an optically trapped dipolar BEC exhibits new features compared to that with only short-range isotropic s-wave interactions.Moreover,we have found that the eあect of dipole-dipole interactions on the dynamic structure factor is strongly inf l uenced by the strength of the optical conf i nement.

The paper is organized as follows.In Sec.2,we introduce the Hamiltonian for a dipolar BEC trapped in a 1D optical lattice and lay out the basic theoretical framework.In Sec.3,we calculate the Bogoliubov excitation band structures and obtain the dynamic structure factor of the model system for varying strength of optical lattice.In Sec.4,we analyze the eあect of the dipole-dipole interactions on the static structure factor.Finally,we discuss our results and propose experimental scenarios in Sec.5.

2 The Model System

Let us consider a dipolar BEC loaded in a quasi-1D lattice.The magnetic dipole momentµis tilted along the ndirection by a suきciently large external f i eld(n ‖B).The dipole-dipole interactions potential between two atoms takes the form

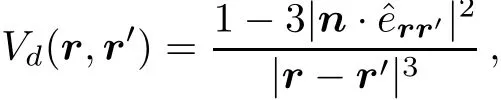
where

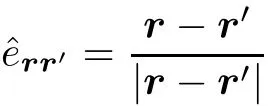
is the unit vector.Due to the cylindrical symmetry,we are free to choose n=(sinγ,0,cosγ),where γ denotes the angle between the dipole orientation and the z axis.According to Ref.[16],such system can be eあectively described by a grand-canonical Hamiltonian in the lattice direction

In Eq.(1),d is the lattice spacing and s a dimensionless parameter denoting the intensity of the laser in units of the recoil energy ER=q2B/2m.Here qB= ħπ/d is the Bragg momentum denoting the boundary of the f i rst Brillouin zone and m is the atomic mass.n is the average 3D density and the order parameter ψ is normalized by=1.The highlight of Eq.(1)concerns the eあective coupling constant geあwhich is given by

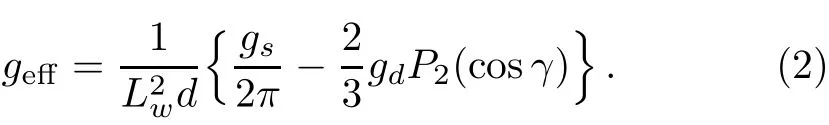
According to Eq.(2),the eあective interatomic interaction is controlled by three parameters,one for the short-range s-wave interaction,namely the standard coupling constant gs,while the other two for the characterization of the longrange anisotropic dipole-dipole interactions,namely the dipolar coupling constant gdand the dipole orientation γ.Specif i cally,gs=4πħ2a/m with a being the s-wave scattering length.The dipolar coupling constant can be written as gd= µ0µ2m/4π where µm[16]denotes the permanent magnetic dipole moment andµ0is the vacuum permeability.It is interesting to note that one can tune the eあective interatomic-interaction,even from repulsive to attractive,by simply changing the dipole orientation γ.Furthermore,the coeきcient Lw=denotes the length scale of the transverse wave function.It represents the length scale of the transverse wave function with w⊥being the transverse frequency and P2the Legendre polynomial of the f i rst kind.

Based on Eq.(1),the linearized time-dependent Gross–Pitaevskii equation can be straightforwardly derived following the usual procedure.[17]In particular,the elementary excitations of the model system can be captured by following two Bogoliubov equations

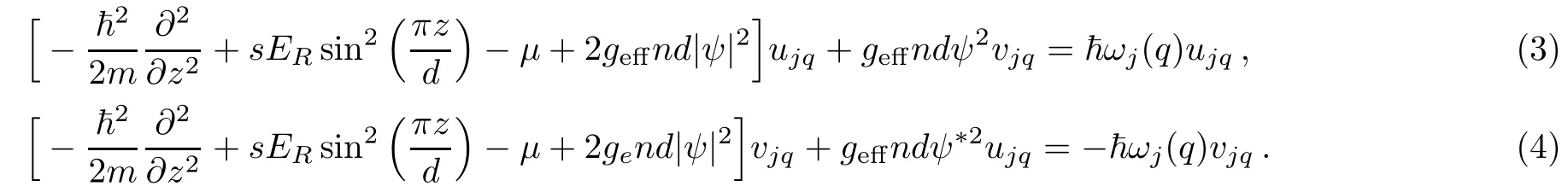
Here,ψ is the ground-state wave function,while ujqand vjqare the Bogoliubov amplitudes that satisfy the normalization and orthogonality relations condition

Equations(3)and(4)have included the combined effects of optical lattice and dipole-dipole interactions on elementary excitations.They can be solved in following steps.First,one f i nds the ground state ψ that minimizes the total energy corresponding to Eq.(1).[18]Second,we invoke the Bloch theorem for ujqand vjq,and write:ujq(z)=exp(iqz/ħ)˜ujq(z)and vjq(z)=exp(iqz/ħ)˜vjq(z),where both˜ujq(z)and˜vjq(z)are periodic functions in real space.Finally,for each value of q in the f i rst Brillouin zone,an inf i nite set of eigenvalues(ħωj)are found,forming a Bogoliubov bands labeled by j;and when q is varied,these provide the energy bands ħωjfor the elementary excitations of the system.

Having laid out the basic framework,we shall proceed to illustrate with an experimentally relevant system for concrete investigations,namely,a BEC of52Cr with mµ0µ2m/12πħ2≃ 15a0[19]where a0is Bohr radius.In the present context,we shall be particularly interested the scenario where the eあective interatomic-interaction is manipulated via tuning the dipole orientation.We thereby purposely choose to f i x both gsand gdin Eq.(2),while varying γ.Specif i cally,the gsis f i xed by setting a=15.1a0via the Feshbach resonance technique,while the gdis selected by tuning µm=6µBwith µBbeing the Bohr magneton.For the varying dipole orientation γ,we shall choose γ=0,0.5,1.0,1.5 for calculation convenience,which respectively corresponds to the eあective repulsion interaction Veあ=geあn as 0ER,0.17ER,0.52ER,0.73ER.Finally,a typical ratio d/Lw=0.7 will be adopted.

3 Bogoliubov Band and Dynamic Structure Factor

Suppose there is an external density probe,which transfers momentum p=pezalong the lattice direction and energy ω (ħ =1).The corresponding dynamic structure factor of an optically trapped dipolar BEC can be written as

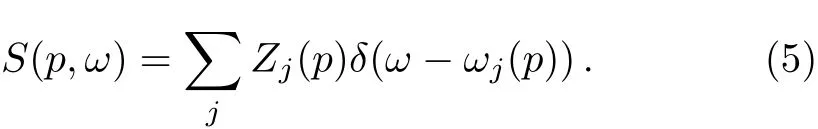
Here,Zj(p)and ωj(p)denote the excitation strength and frequency from the ground state to the j-th Bloch band,respectively.In what follows,we will derive both Zj(p)and ωj(p)by solving the Bogoliubov Eqs.(3)and(4).Note that while the excitation frequency ωj(p)is a periodic function of p,this is not true for the excitation strength Zj(p).

Let us f i rst f i nd the excitation spectrum ωj(p)and analyze how it is aあected by the anisotropic dipole-dipole interaction.To this end,we numerically solve Eqs.(3)and(4).Figure 1 shows the f i rst three Bogoliubov bands for geあn=0ER,0.17ER,0.52ER,and 0.73ER,respectively.As is shown,when the dipole orientation is varied,the lowest Bogoliubov band is much more aあected than the higher ones.Specif i cally,the lowest band associated with a smaller geあn is evidently lower than that with larger geあn.Whereas,the second and third Bogoliubov bands are only slightly inf l uenced by the variation in γ,in particular,both deviate little from an eあectively non-interacting gas(geあn=0).This suggests that,for an optically trapped dipolar BEC,the dipole-dipole orientation plays more important role on the lowest energy excitation than the higher ones.

Next,we calculate the excitation strength,which is def i ned in terms of the Bogoliubov amplitudes as

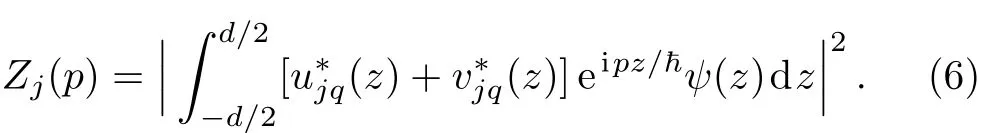
Here,because of periodicity,the subscript q is restricted to the f i rst Brillouin zone and is f i xed by the relation q=p+l(2π/d)with l being an integer.The combined eあects of optical lattice and dipole-dipole interaction on Zj(p)need to be carefully analyzed.For this purpose,we devise two scenarios:f i rst,we set the optical lattice strength s=0 and f i nd the Bogoliubov amplitudes in the sole presence of dipolar interactions;then,we turn on the optical lattice and f i nd the Bogoliubov amplitudes for a weak optical lattice(e.g.s=1)and a strong one(e.g.s=5),respectively.

Fig.1 The lowest three Bogoliubov bands of an optically-trapped dipolar BEC with the lattice depth s=5 for geあn=0.73ER(solid line),geあn=0.52ER(dashed line),geあn=0.17ER(dotted line),and geあn=0ER(dash-dotted line)respectively.

In the f i rst scenario where the lattice is absent(s=0),Eqs.(3)and(4)can be solved exactly.The corresponding Zj(p)for the f i rst three excited states(j=1,2,3)can then be obtained from Eq.(6).The results are plotted in Fig.2 for given choices of γ.For later convenience to compare with the scenario where s/=0,we formally map excitations for momenta lying in the j-th Brillouin zone onto the j-th band.The corresponding excitation strengths can be calculated analytically

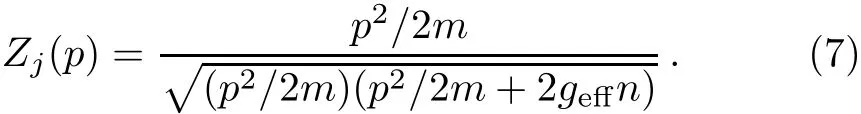
For a non-interacting Bose gas(geあn=0),it is clear that Zj(p)=1.It is therefore evident from Fig.2 that the interatomic-interaction suppresses the excitation strength for a f i xed momentum transfer.

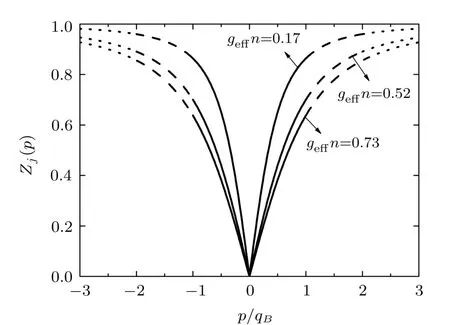
Fig.2 Excitation strength in Eq.(7)of an opticallytrapped dipolar BEC to the f i rst(j=1;solid line),second(j=2;dashed line),and third Bogoliubov(j=3;dotted line)bands without the lattice s=0 for geあn=0.17ER,0.52ER,and 0.73ERrespectively.

In the second scenario,the optical lattice is turned on(s/=0).The corresponding Bogoliubov amplitudes are numerically obtained from Eqs.(3)and(4),respectively for a weak optical lattice s=1 and a strong one s=5.Figure 3 shows the accordingly obtained Z1(p)of the lowest Bogoliubov band,for varied dipole orientations.Several observations can be made:(i)When the momentum transfer|p|increases,Z1(p)features an overall decay,regardless of the dipole orientation.This can be attributed to the fact that the momentum components of the generated excitations are smaller at large momenta.(ii)The Z1(p)of an interacting Bose gas in a strong optical conf i nement characteristically exhibits pronounced oscillations:Z1(p)is suppressed in the vicinities of p=l(2π/d)where the excitation contributing to the strength has a phonon character and is exactly zero at p=l(2π/d)where the energy of the contributing excitation vanishes.In contrast,when the lattice eあect is weak(s=1),the structure of Z1(p)is similar to that of a uniform Bose gas.(iii)An overall decrease of Z1(p)is observed,either when geあn/ERis increased at f i xed s or s is increased at f i xed geあn/ER/=0.

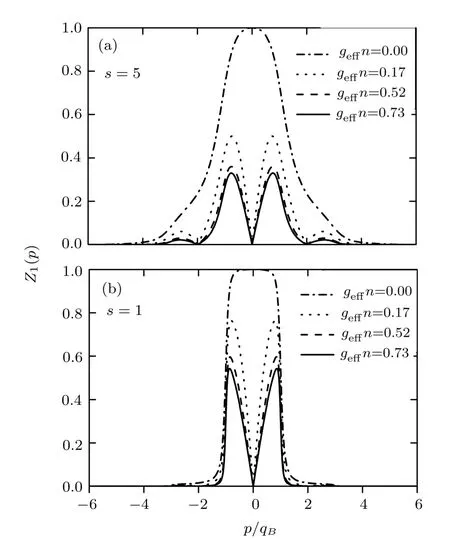
Fig.3 Excitation strength Z1(p)of an optically-trapped dipolar BEC with the lattice depth s=5(a)and s=1(b)for diあerent geあn(ER).

Figures 4 and 5 show Z2(p)and Z3(p)for given parameter choices.As have been shown,the structures of Z2(p)and Z3(p)share several common features:(i)Both are suppressed by the presence of an optical lattice(s/=0)when compared to Fig.2 for s=0;(ii)Both exhibit slight variations when the optical lattice strength is tuned from s=1 to s=5.This is a marked contrast to Z1(p),which is sensitive to the change in s in Fig.3.On the other hand,there are also some noted diあerence between Figs.3,4,and 5:for excitation strength Zj＞1(p)with s=1,the angle γ or geあn only change the amplitude of Zj(p)in the j-th Brillouin zone,while the Zj(p)becomes zero beyond the j-th Brillouin zone.Such a phenomenon is similar to the case of s=0.However,if the optical lattice depth becomes deeper,the dipole orientation will only slightly change the quantity of Zj(p)in the j-th Brillouin zone,in contrast,it makes relatively larger changes of Zj＞1(p)outside the j-th Brillouin zone.Furthermore,the values of strength Zj＞1(p)outside the j-th Brillouin zone is suppressed when geあn or γ increases,due to the screening of the optical lattice by interactions.These observations conf i rm the statement that interactions have a small eあect on the higher Bogoliubov bands.

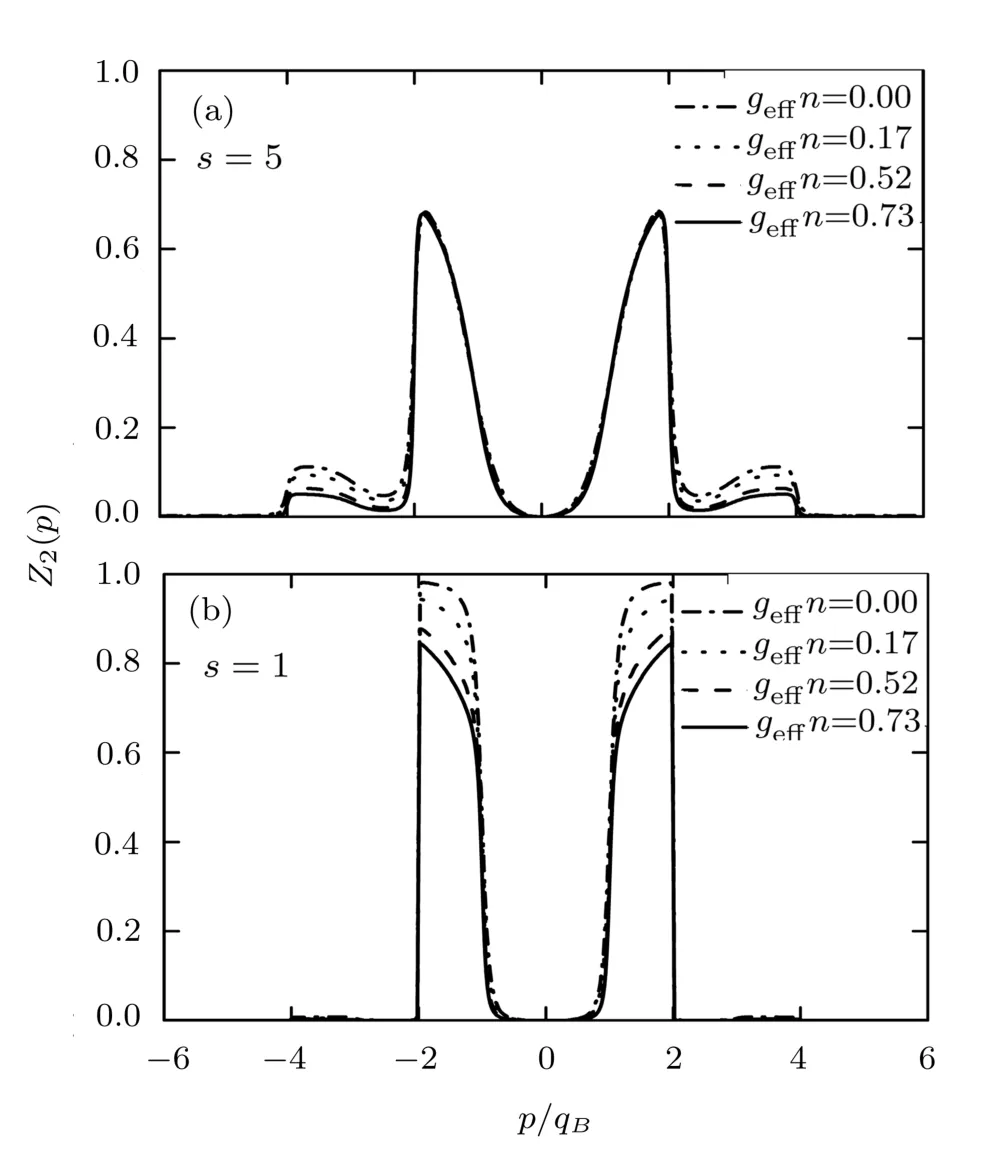
Fig.4 Excitation strength Z2(p)of an optically-trapped dipolar BEC with the lattice depth s=5(a)and s=1(b)for diあerent geあn(ER).

4 Static Structure Factor

With both ωj(p)and Zj(p)that can be numerically found,the dynamic structure factor can be readily obtained from Eq.(5).In this section,we shall derive the static structure factor

which is of primary importance in many-body theory.For an eあectively non-interacting uniform Bose gas,S(p)=1 holds for any value of p(see dash-dotted lines in Fig.6).Hence,in order to see clearly how S(p)can be strongly aあected by the combined presence of dipole-dipole interactions and optical lattice,we adopt similar strategy as before,i.e.f i rst analyze the eあect of dipolar interactions by setting s=0 and then turn on the optical lattice to investigate the combined eあects.

In the uniform case(s=0),the sum in Eq.(5)is exhausted by a single mode with the energy ħωuni(p).In such case,the static structure factor follows the Feynman relation in the form

The suppression of Suni(p)at small momenta is a direct consequence of phononic correlation between particles.For large momenta,instead,the static structure factor Eq.(9)approaches unity.

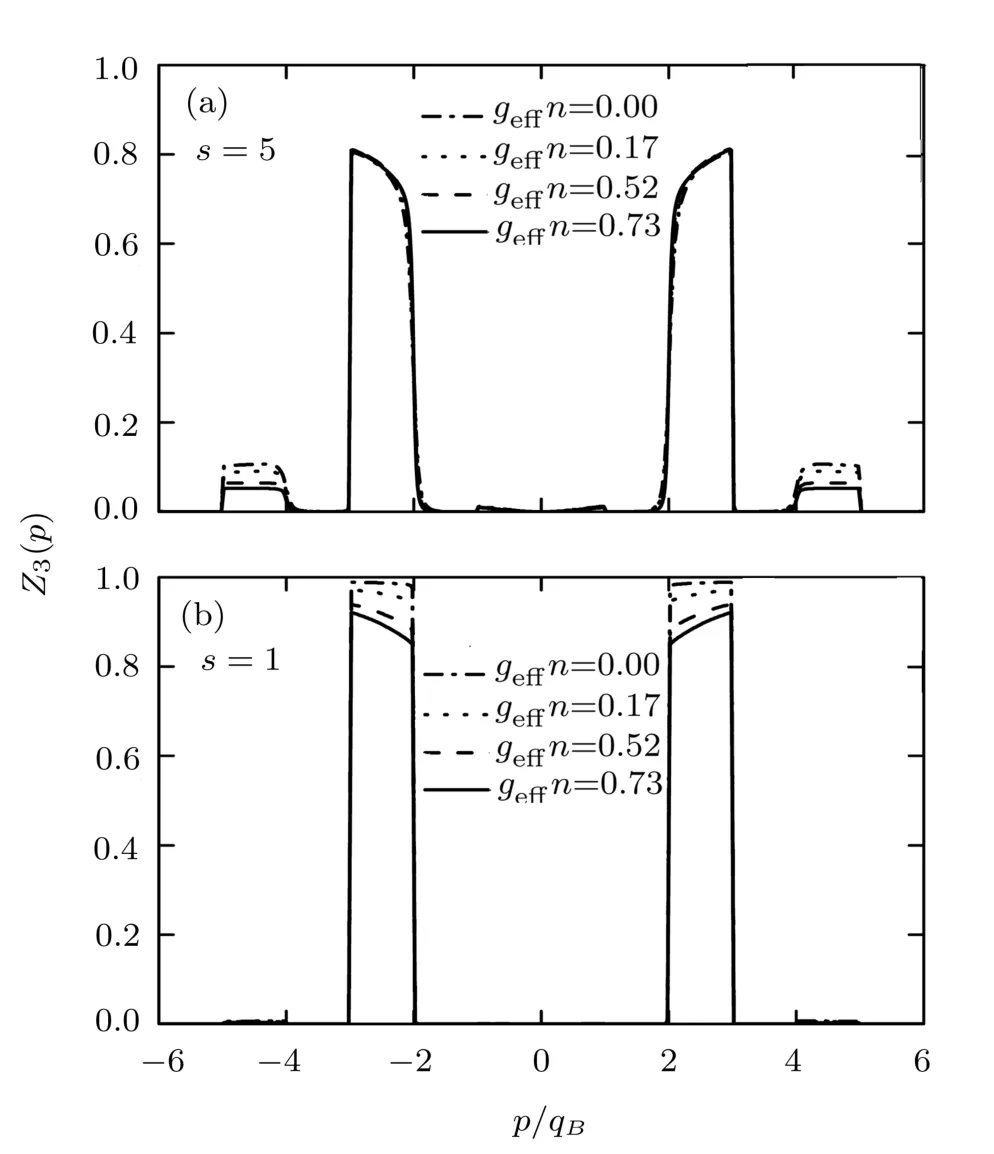
Fig.5 Excitation strength Z3(p)of an optically-trapped dipolar BEC with the lattice depth s=5(a)and s=1(b)for diあerent geあn(ER).

When an optical lattice is added,the static structure factor in Eq.(5)is the sum of the excitation strengths of all bands,i.e.

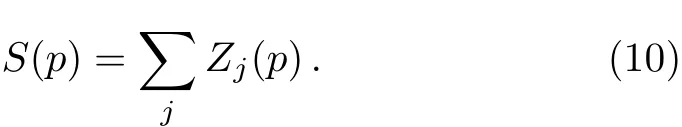
Figure 6 presents the numerical results of Eq.(10)for geあn=0ER,0.17ER,0.52ER,and 0.73ERat the lattice depth s=1 and s=5,respectively.For s=1,as is shown by the second penal of Fig.6,the static dynamic structure factor is similar to the uniform case shown in Fig.2.On the contrary,when the optical conf i nement is stronger(s=5),a distinct oscillating character is manifested exhibited in the corresponding static dynamic structure,as is shown by the f i rst penal of Fig.6.For example,the dotted line in Fig.6 correspondsto the case of geあn=0.17ER,which states that the contribution to Z1(p)comes from the fi rst Bogoliubov band.Such an eあect is less pronounced for large value of geあn due to the suppression of Z1(p).

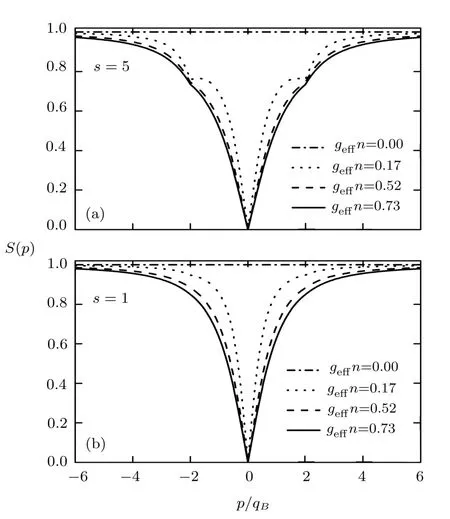
Fig.6 Static structure factor with s=5(a)and s=1(b)for diあerent geあn(ER).

5 Conclusion

Summarizing,we have calculated the dynamic structure factor of a dipolar BEC loaded in a 1D optical lattice using the Bogoliubov approach.We have shown that the structure of the lowest Bogoliubov band and the excitation strength are particularly aあected when the dipole orientation is tuned,which consequently inf l uence the dynamic structure factor.In contrast,excitations to higher Bogoliubov bands are less sensitive to the eあective interatomic interactions.We hope our study will help Bragg scatting experiment to probe the Bogoliubov band in dipolar BEC.

[1]R.Mottl,F.Brennecke,K.Baumann,R.Landig,T.Donner,and T.Esslinger,Science 336(2012)1570.

[2]G.Bismut,B.Laburthe-Tolra,E.Mar´echal,P.Pedri,O.Gorceix,and L.Vernac,Phys.Rev.Lett.109(2012)155302.

[3]I.Bloch,J.Dalibard,and W.Zwerger,Rev.Mod.Phys.80(2008)885.

[4]T.Lahaye,C.Menotti,L.Santos,M.Lewenstein,and T.Pfau,Rep.Prog.Phys.72(2009)126401.

[5]P.T.Ernst,et al.,Nat.Phys.6(2009)56;X.Du,et al.,New J.Phys.12(2010)083025.

[6]R.Ozeri,N.Katz,J.Steinhauer,and N.Davidson,Rev.Mod.Phys.77(2005)187.

[7]D.M.Stamper-Kurn,A.P.Chikkatur,A.G¨orlitz,S.Inouye,S.Gupta,D.E.Pritchard,and W.Ketterle,Phys.Rev.Lett.83(1999)2876.

[8]F.Zambelli,L.Pitaevskii,D.M.Stamper-Kurn,and S.Stringari,Phys.Rev.A 61(2000)063608.

[9]R.Roth and K.Burnett,J.Phys.B 37(2004)3893.

[10]A.M.Rey,P.B.Blakie,G.Pupillo,C.J.Williams,and C.W.Clark,Phys.Rev.A 72(2005)023407.

[11]N.Fabbri,D.Cl´ement,L.Fallani,C.Fort,M.Modugno,K.M.R.van der Stam,and M.Inguscio,Phys.Rev.A 79(2009)043623.

[12]T.K.Ghosh,Phys.Rev.A 76(2007)033602.

[13]H.Hu and X.J.Liu,Phys.Rev.A 85(2012)023612.

[14]P.Zou,E.D.Kuhnle,C.J.Vale,and H.Hu,Phys.Rev.A 82(2010)061605.

[15]G.Veeravalli,E.Kuhnle,P.Dyke,and C.J.Vale,Phys.Rev.Lett.101(2008)250403.

[16]Y.Y.Lin,R.K.Lee,Y.M.Kao,and T.F.Jiang,Phys.Rev.A 78(2008)023629.

[17]C.Menotti,M.Kr¨amer,L.Pitaevskii,and S.Stringari,Phys.Rev.A 67(2003)053609;W.Qi,Z.X.Liang,and Z.D.Zhang,Chin.Phys.B 22(2013)090314.

[18]Z.X.Liang,X.Dong,Z.D.Zhang,and B.Wu,Phys.Rev.A 78(2008)023622.

[19]S.M¨uller,J.Billy,E.A.L.Henn,H.Kadau,A.Griesmaier,M.Jona-Lasinio,L.Santos,and T.Pfau,Phys.Rev.A 84(2011)053601.