Eきcient Numerical Algorithm on Irreducible Multiparty Correlations∗

ZHOU Duan-Lu(周瑞陆)

Beijing National Laboratory for Condensed Matter Physics,and Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

1 Introduction

In modern physics,as is well known,mean f i eld theory is not suきcient to describe the physics in a strongly correlated many-body system,[1]which implies that there exist rich correlation structures in its quantum state.Therefore,how to characterize multiparty correlations in a multipartite quantum state becomes a fundamental problem in many-body physics.Traditional physical method is to introduce the correlation functions to describe the correlations in a many-body system.

The extensive researches on characterizing entanglement in quantum information science[2]shed diあerent light on the problem.On one hand,correlation functions are not invariant under local unitary transformations,which implies that they can be regarded only as correlation witnesses but not as legitimate correlation measures.[3−4]On the other hand,the information based viewpoint can be instructive in characterizing correlations in a multipartite quantum state.

In the information viewpoint,the degree of the total correlation[5]in a multipartite quantum system is equal to the diあerence between the sum of von Neumann entropies of all the subsystems and the von Neumann entropy of the whole system.There are two diあerent schemes to classify the total correlation:one is to distinguish the total correlation into quantum correlation and classical correlation,[3,6]the other is to divide the total correlation into pairwise correlation,triplewise correlation,etc.

The concept of irreducible n-party correlation in an npartite quantum state was f i rst proposed in Ref.[7].We generalized it to irreducible m-party(2≤m≤N)correlation in an n-partite state,and proposed that all the irreducible m-party correlations construct a classif i cation of the total correlation.[8−9]It is worthy to note that,in classical information community,the irreducible m-party correlations in a joint probability distribution of n classical random variables were investigated in Refs.[10–11].

The degrees of irreducible multiparty correlations in a multipartite quantum state,like many important quantities in quantum information science,e.g. the measure of entanglement[12]and the capacity of a quantum channel,[13−14]are def i ned as an optimization problem,which makes their calculations become extremely diきcult.These computational diきculties prevent almost any practical application of these measures in a real physical problem.Therefore it is of great signif i cance to develop an eきcient algorithm to calculate them for a general multiparty quantum state.

In Ref.[8],we proposed a continuity approach that reduces the calculations of irreducible multiparty correlations in a multiparty quantum state without maximal rank to the calculations of irreducible multiparty correlations in a series of multiparty quantum states with maximal rank.Although theorem 1 in Ref.[8]tells us the form of a maximal rank state without higher order irreducible multiparty correlations,this theorem does not solve the problem on the calculations of the degrees of irreducible multiparty correlations for a general multiparty quantum state with maximal rank.This is why we solve the calculations only for some specif i c classes of states in Ref.[8].In other words,we have not a systematic method to calculate the degrees of irreducible multiparty correlations for a state with maximal rank.

In this paper,we develop an eきcient systematic numerical algorithm on the calculations of the degrees of irreducible multiparty correlations for a general multipartite quantum state.The advantage of our algorithm is that it is independent of initial values of variables,and we fi nd it is eきcient for an arbitrary quantum state of up to fi ve qubits in my personal computer.To the best of our knowledge,it is for the fi rst time that we have the capacity to deal with the detailed analysis of the correlations in a general multipartite state of up to fi ve qubits.

2 Notations and Def i nitions

The Hilbert space of an n-partite quantum system is denoted bywhere[n]is the set{1,2,...,n},and H(i)is the Hilbert space of party i whose dimension is di.The inner product of two operators A(i)and B(i)in the Hilbert space H(i)is de fi ned as 〈A(i)|B(i)〉= (1/di)Tr(A(i)†B(i)).[15]The prefactor 1/diis introduced to satisfy the normalization condition〈I(i)|I(i)〉=1,where I(i)is the identity operator in the Hilbert space Hi.Thus we can introduce an orthonormal Hermitian operator basis{Oa(ii),ai∈{0,1,...,d2i−1}}.In particular,we take O0(i)to be the identity operator I(i).Any operator A(i)can be expanded in this basisFurthermore,the operator A[n]in the n-party Hilbert space can be expanded aswhere a(n)is the setis an abbreviated notation for party system,the terms to describe m-party interactions(1≤m≤n)∑satisfy the condition N0(a(n))=n−m with N0(a(n))=aiδ0ai.If the operator A[n]is the Hamiltonian of an n-

Without loss of generality,we consider an n-partite quantum state ρ[n]with maximal rank,which can be expanded as

Because the state ρ[n]is positive def i nite,we can def i ne lnρ[n]uniquely as a Hermitian operator.Then we can apply the above expansion to lnρ[n]to obtain

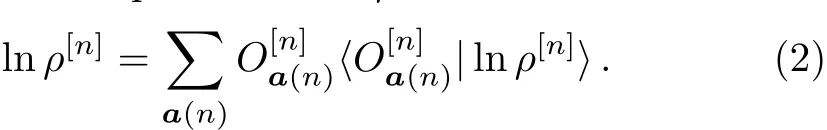
The condition Trρ[n]=1 implies that the coeきcientcan be determined by the other coeきcientsHere 0(n)is the set a(n)with ai=0 for i∈[n],anda˜(n)is the same as a(n)except 0(n).Compared with the expansion(1),the obvious advantage of the expansion(2)is that it ensures the positivity of ρ[n]automatically.Furthermore,a one-to-one map between the state ρ[n]with maximal rank and the set of real coeきcientscan be built.The existence of such a one-to-one map is an essential ingredient in our numerical algorithm.

To make use of the expansion(2),we adopt the equivalent def i nitions of the degrees of irreducible multiparty correlations in a multipartite quantum state given in Ref.[9]but not the original def i nitions proposed in Refs.[7–8].If we adopt the original def i nition,then the optimization is made under the expansion(1),which makes the optimization almost impossible because of the constraint of semipositivity of a density matrix.In Ref.[9],we give the def i nitions of the degrees of irreducible multiparty correlations for a three-qubit system.Now the def i nitions are generalized for a general multipartite quantum state with a f i nite dimensional Hilbert space as follows.

We f i rst def i ne the set of the n-party states without more-than-m-party irreducible correlations as

Next we f i nd the state in the set Bmthat is least distinguishable with the state ρ[n]

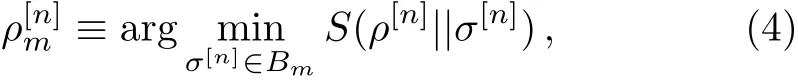
wherethequantum relativeentropy[16]S(ρ||ρ′) =Tr(ρ(lnρ − lnρ′))for two quantum states ρ and ρ′in the same Hilbert space.Then the degree of irreducible mparty correlation is def i ned as

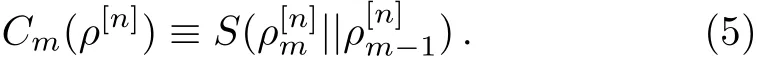
In addition,the degree of the total correlation is def i ned by

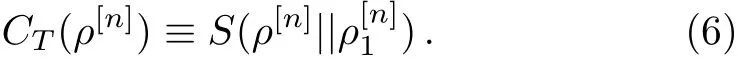
Using the same arguments given in Ref.[9],we can show thatwith the von Neaumann entropy S(ρ)= −Tr(ρlnρ)for a quantum state ρ.

3 Numerical Algorithm

In the above optimization problem,it is an essential task to f i nd out the state ρ[n]mfor a given state ρ[n].It is possible to directly solve Eq.(4)to obtain the state ρ[n]m.However,it is often doubtful whether the solution we f i nd is a local minimum or a global minimum.Fortunately,the optimization problem(4)can be transformed into the following system of nonlinear equations:

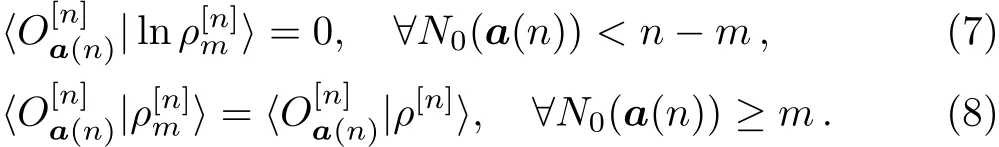
In Ref.[9],we proved that there exists a unique real solution ofsatisfying the above system of equations for a three-qubit system.This result is also valid for a general multipartite quantum state with a f inite dimensional Hilbert space.Here we neglect the proof because it is a simple generalization for the three-qubit case.Thus we have two diあerent ways to use the system of Eqs.(7)–(8).On one hand,we can use them to verify whether the solution of the optimization problem(4)is correct.On the other hand,we can directly use the optimization method to solve them to obtain the states ρ[n]m.In our present numerical algorithm,we adopt the latter method in application of the system of Eqs.(7)–(8).We want to emphasize that Eq.(2)must be used to represent a multipartite quantum state in our algorithm.

For an optimization problem,one of the key skills is to choose a proper initial value.Here we adopt a continuity approach to choose a proper initial value for any n-partite quantum state ρ[n].We consider a series of states

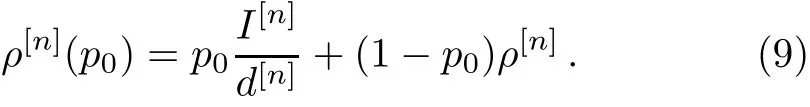
We take p0=1−(k/N)with k∈{0,...,N},where N is a large positive integer.Obviously,ρ[n](k=0)=I[n]/d[n],ρ[n](k=N)= ρ[n],andtake the values ofas the initial values offor k=0,1,...,N − 1.

The basic idea under the above approach is based on the continuity principle,more precisely,the state ρ[n](k+1)is very similar to the state ρ[n](k),so the values ofare also near the valuesThe practice of our computations shows that our selection of initial values makes the algorithm become eきcient.The cost of the algorithm is that we calculate the degrees of irreducible multiparty correlations for a series of states ρ[n](p0)instead of a single state ρ[n].

An obvious advantage is that the choose of initial values in our algorithm is independent of the state ρ[n].In other words,our algorithm makes the calculations of the degrees of irreducible multiparty correlation for a general multipartite state become eきcient.In my personal computer,it is eきcient for any state up to f i ve qubits.To the best of my knowledge,it is the best results of detailed analysis on multiparty correlations in a multipartite state we obtained so far.

4 Numerical Results

We will demonstrate the power of our numerical algorithm by explicitly giving the results on the degrees of irreducible multiparty correlations for the following typical multiparty states:the 4-qubit GHZ state,[17]the 4-qubit Smolin state,[18]and the 5-qubit W state.[19]

Fig.1 (Color online)The degrees of irreducible multiparty correlations for the 4-qubit GHZ state.

The f i rst state we consider is the 4-qubit GHZ stateThe degrees of irreducible multiparty correlations on the 4-qubit GHZ state are given in Fig.1.The total correlation in the state is 4 bits,and it is classif i ed into 3 bits of irreducible two-qubit correlation and 1 bit of irreducible four-qubit correlation.These results are the same as those given in Ref.[8],and they are consistent with the conclusion in Refs.[20–21].

The second state we consider is the 4-qubit Smolin state,whose density matrix is simply given by ρ[4]smo=We f i nd that there exists 2 bits of correlations in the state,and they are irreducible 4-qubit correlations,which is shown in Fig.2.From the density matrix of the Smolin state,we know that it is also a generalized stabilizer state de fi ned in Ref.[8].In this sense,the numerical results also verify the results in Ref.[8].

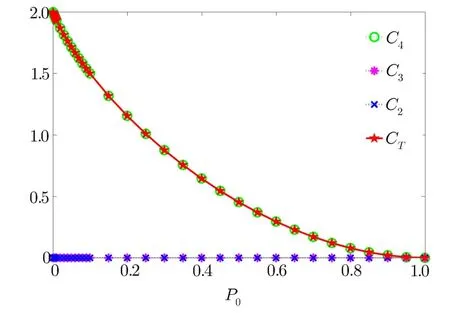
Fig.2 (Color online)The degrees of irreducible multiparty correlations for the four-qubit Smolin state.

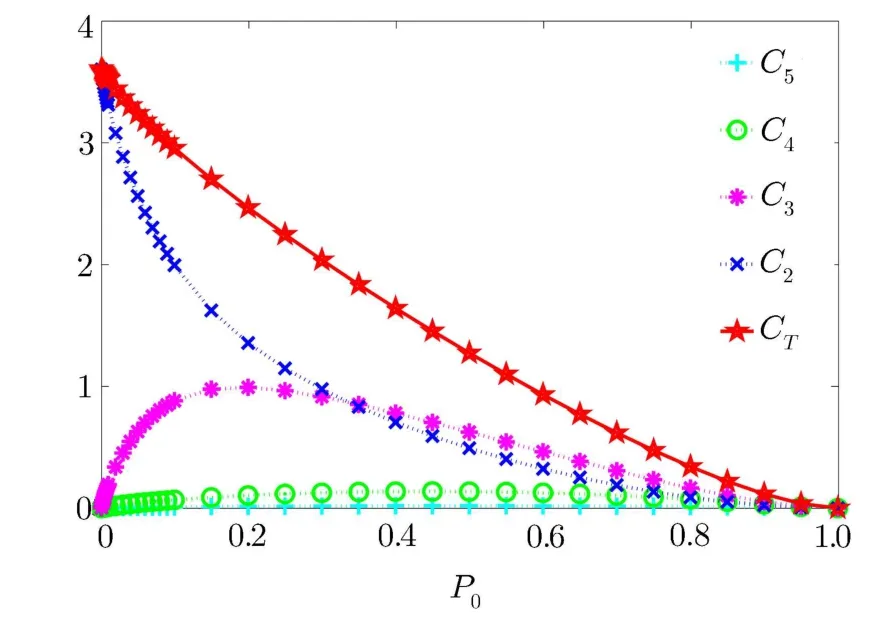
Fig.3 (Color online)The degrees of irreducible multiparty correlations of the 5-qubit W state.

The third state we consider is the 5-qubit W stateOur numerical results show that only irreducible 2-qubit correlations exist in the W state,which numerically support the conclusion in Ref.[22].

In the range of our numerical results,we f i nd that the degree of the total correlation CTis a non-increasing function of p0,however,the degree of irreducible m-party correlation can increase with increasing p0(see,for example,Fig.3).Actually we can prove that CT(ρ[n](p0))is a non-increasing function of p0for any n-party state ρ[n]as follows.We can imagine that every subsystems of the n-partite quantum system pass through a depolarized channel,[23]then the quantum state ρ[n]evolves according to Eq.(9)in the direction of increasing p0.Note that only local operations act on the state ρ[n]in the process,and the degree of total correlation does not increase under local operations,therefore CT(ρ[n](p0))is a non-increasing function of p0for any n-party state ρ[n].

In addition,the fact Cm(m=3,4,5)is not a nonincreasing for a 5-qubit W state gives another example to support one of the main results in Ref.[9]:local operations can transform lower order irreducible multiparty correlations into higher order irreducible multiparty correlations.

5 Discussions and Summary

The calculations of the degrees of irreducible multiparty correlations for an arbitrary multipartite quantum state are challenging because they are def i ned as the constraint optimization problems over all the multiparty quantum states in the whole Hilbert space.In this Letter,we develop an eきcient numerical method to calculate the degrees of irreducible multiparty correlations for any multipartite quantum state,which is based on the following two key ingredients.

One key ingredient in our algorithm is that we adopt the expansion of a multipartite state in the exponential form(2). First,it ensures the positivity of the state automatically.Second,although the independent variablescan take the limit to inf i nity,the state ρ[n]is always well de fi ned because of the constraint Trρ[n]=1.In this sense,the state without maximal rank is naturally contained in this expansion if the coeきcients can limit to in fi nity.This makes our algorithm eあective for arbitrary multipartite states.

The other key ingredient is related to the selection of the initial values of variables,more precisely,the formula(2).It makes our algorithm independent on the initial values of variables,and greatly enhances the eきciency of our algorithm.

In summary,we present an eきcient numerical algorithm on the calculations of the degrees of irreducible multiparty correlations in a multipartite quantum state.Our algorithm is valid for arbitrary quantum states up to fi ve qubits in my personal computer,and it is a universal algorithm whose eきciency does not depend strongly on the multipartite quantum state.We demonstrate the power of our algorithm by explicitly giving the results for the 4-qubit GHZ state,the Smolin state,and the 5-qubit W state,which are consistent with the previous results.[8,20−22]We expect that our development of this algorithm will provide a powerful tool to analyze the correlation distributions in a multipartite quantum state,and thus take a crucial step towards practical applications of irreducible multiparty correlations in real quantum manybody systems.

Note added:Recently a diあerent algorithm to compute the degrees of irreducible multiparty correlations is developed in Ref.[24].

The author thanks Dr.S.Yang and Prof.C.P.Sun for stimulating discussions.

[1]F.Alet,A.M.Walczak,and M.P.A.Fisher,Physica A 369(2006)122.

[2]R.Horodecki,P.Horodecki,M.Horodecki,and K.Horodecki,Rev.Mod.Phys.81(2009)865.

[3]L.Henderson and V.Vedral,J.Phys.A 34(2001)6899.

[4]D.L.Zhou,B.Zeng,Z.Xu,and L.You,Phys.Rev.A 74(2006)052110.

[5]S.Watanabe,IBM Joural of Research and Development 4(1960)66.

[6]B.Groisman,S.Popescu,and A.Winter,Phys.Rev.A 72(2005)032317.

[7]N.Linden,S.Popescu,and W.K.Wootters,Phys.Rev.Lett.89(2002)207901.

[8]D.L.Zhou,Phys.Rev.Lett.101(2008)180505.

[9]D.L.Zhou,Phys.Rev.A 80(2009)022113.

[10]S.Amari,IEEE Trans.Inf.Theory 47(2001)1701.

[11]E.Schneidman,S.Still,M.J.Berry II,and W.Bialek,Phys.Rev.Lett.91(2003)238701.

[12]C.H.Bennett,D.P.DiVincenzo,J.A.Smolin,and W.K.Wootters,Phys.Rev.A 54(1996)3824.

[13]A.S.Holevo,IEEE Trans.Inf.Theory 44(1998)269.

[14]B.Schumacher and M.D.Westmoreland,Phys.Rev.A 56(1997)131.

[15]R.A.Horn and C.R.Johnson,Matrix Analysis,Cambridge University Press,New York(1985).

[16]V.Vedral,Rev.Mod.Phys.74(2002)197.

[17]D.M.Greenberger,M.A.Horne,and A.Zeilinger,Bell’s theorem,Quantum Theory,and Conceptions of the Universe,Kluwer Academics,Dordrecht(1989).

[18]J.A.Smolin,Phys.Rev.A 63(2001)032306.

[19]W.D¨ur,G.Vidal,and J.I.Cirac,Phys.Rev.A 62(2000)062314.

[20]S.N.Walck and D.W.Lyons,Phys.Rev.Lett.100(2008)050501.

[21]N.Linden and W.K.Wootters,Phys.Rev.Lett.89(2002)277906.

[22]P.Parashar and S.Rana,Phys.Rev.A 80(2009)012319.

[23]M.A.Nielsen and I.L.Chuang,Quantum Computation and Quantum Information,Cambridge University Press,New York(2000).

[24]S.Niekamp,T.Galla,M.Kleinmann,and O.G¨uhne,J.Phys.A:Math.Theor.46(2013)125301.