载人深空探测进入/再入走廊设计方法研究

侯砚泽 左光 王平 向开恒 果琳丽

（北京空间技术研制试验中心，北京 100094）

0 引言

载人深空探测进入/再入过程中，载人航天器必须满足进入/再入走廊约束，以避免经历过大的过载、热流和总加热量等力/热环境，威胁进入/再入飞行安全[1-4]。进入/再入走廊设计是一项涉及热防护、气动、导航制导与控制、回收等多个技术领域的总体技术。传统的返回舱再入走廊设计主要满足过载、热流密度、总加热量、横向机动能力等设计约束，不关注落点精度和进入/再入走廊设计裕度等问题。然而，随着深空探测进入/再入任务总体指标的不断提高，特别是载人深空探测进入/再入对返回舱行星际进入或再入返回提出了高精度、高可靠定点着陆的技术要求[2,5-6]。在开展进入/再入走廊设计时，必须确保进入/再入走廊在满足过载、热流密度、总加热量、横向机动能力等传统设计约束的同时，满足高精度着陆指标要求；并掌握各项进入/再入偏差对进入/再入走廊的影响，获取进入/再入走廊的设计裕度，明确进入/再入走廊设计结果的可靠性。

为适应上述新的设计要求，本文提出载人深空探测进入/再入走廊的仿真设计方法，在进入/再入走廊仿真分析中融合预测校正制导律，以准确反映不同进入/再入飞行条件下的落点散布，确保进入/再入走廊设计的可行性；同时，引入基于安全系数的偏差因素影响分析方法，通过偏差影响分析，直接反映进入/再入走廊的设计裕度，确保进入/再入走廊设计的可靠性。本文的研究工作将为载人深空探测进入/再入走廊设计及再入返回总体设计提供技术参考。

1 进入/再入走廊设计方法

进入/再入走廊指返回舱进入/再入大气时刻进入/再入角的允许范围。其中，进入/再入时刻定义为返回舱距离当地水平面为特定高度（例如，深空返回取120km）的时刻；进入/再入角定义为返回舱相对大气的飞行速度与当地水平面之间的夹角，相对飞行速度在当地水平面之上时，进入/再入角为正。

进入/再入走廊的分析与设计涉及因素众多，需要结合返回舱总体参数、气动参数、大气密度等设计条件和各项设计条件的偏差情况综合确定，保证进入/再入走廊内的过载、热流密度、总加热量、纵向航程、横向机动能力、落点精度等参数满足设计约束。

进入/再入走廊设计方法分为两类：

1）解析法。通过返回舱进入/再入飞行动力学方程的解析解，计算进入/再入过程中的过载、热流密度、总加热量等参数，进而确定满足设计约束的进入/再入走廊；

2）数值法。通过数学仿真直接计算不同进入/再入条件下的飞行参数，进而确定进入/再入走廊。

解析法在再入走廊设计领域得到了广泛的应用，但是随着深空探测任务落点精度要求、飞行可靠性要求的提升，其方法本身的不足逐步显现出来。利用解析法开展进入/再入走廊分析时必须对飞行动力学方程进行诸多简化，无法全面体现返回舱的动力学特性，也难以全面准确地分析偏差作用下的落点精度和偏差因素影响程度。与此相对应，数值法可以全面体现复杂的进入/再入飞行动力学特性，而且可方便的融入各类制导算法，从而能准确给出进入/再入走廊的落点精度。更为重要的是，数值法可以利用计算机开展大规模偏差仿真分析，充分掌握各项偏差因素影响，进而确定进入/再入走廊的设计裕度。

考虑到前述数值法的技术优势，本文基于数值法开展进入/再入走廊的设计方法研究。

载人深空探测进入/再入走廊的设计是反复迭代的过程，需要综合总体、导航制导与控制、气动、热防护等多个领域的设计要求，经过若干阶段完成设计。基于数值法的载人深空探测进入/再入走廊设计可以划分为初步设计、精细设计和设计验证3个阶段，流程图见图1。

图1中进入/再入走廊基本设计方法中涉及的设计条件和设计约束可分别参见表1和表2。

结合图1，阐述基于数值法的载人深空探测进入/再入走廊初步设计、精细设计和设计验证方法。

（1）初步设计

初步设计中，重点考虑过载、热流密度和大气捕获3项约束条件，其中，过载和大气捕获是强约束条件，一般满足过载约束，也容易满足热流密度约束。

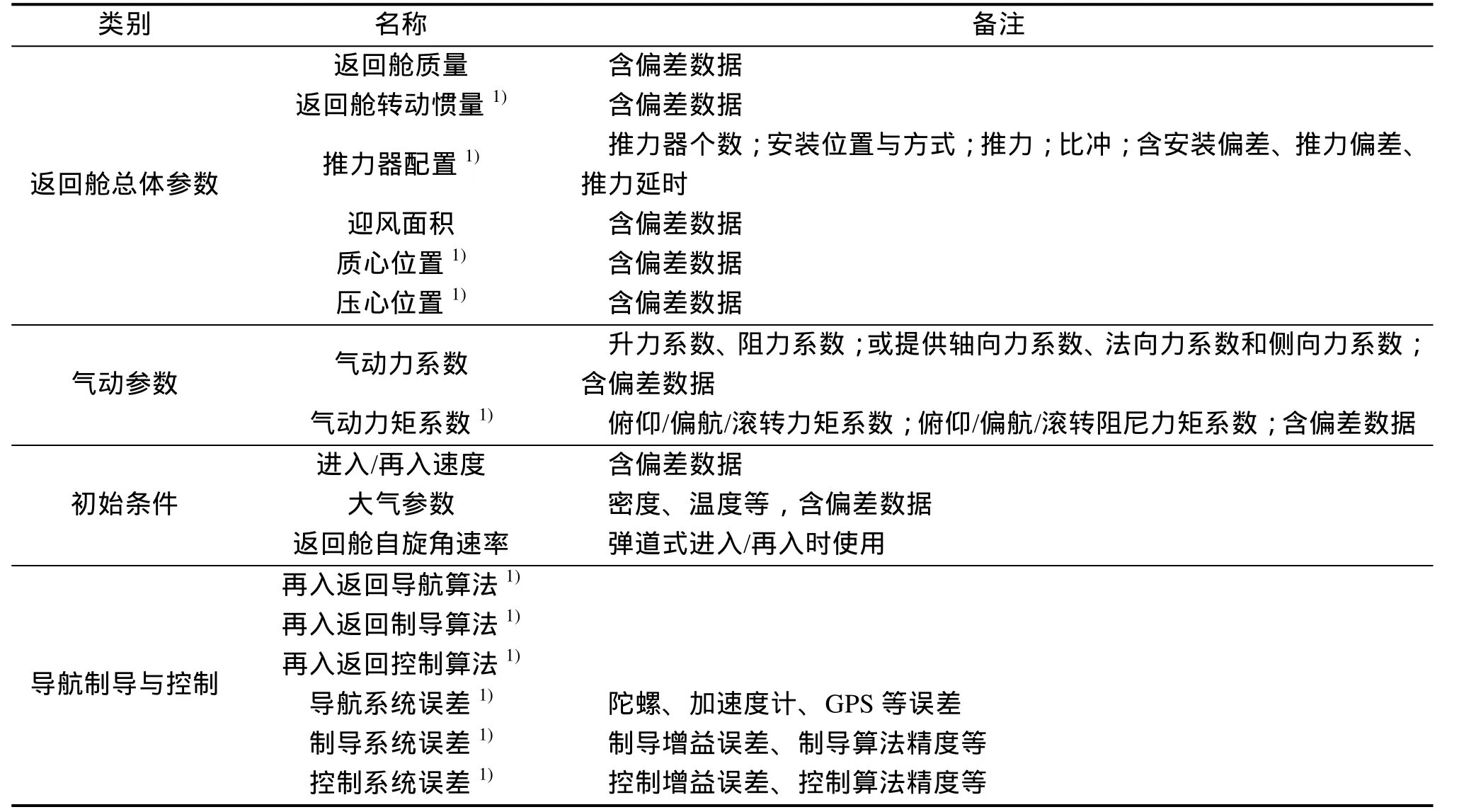
表1 进入/再入走廊的设计条件Tab.1 Design conditions of entry/reentry corridor

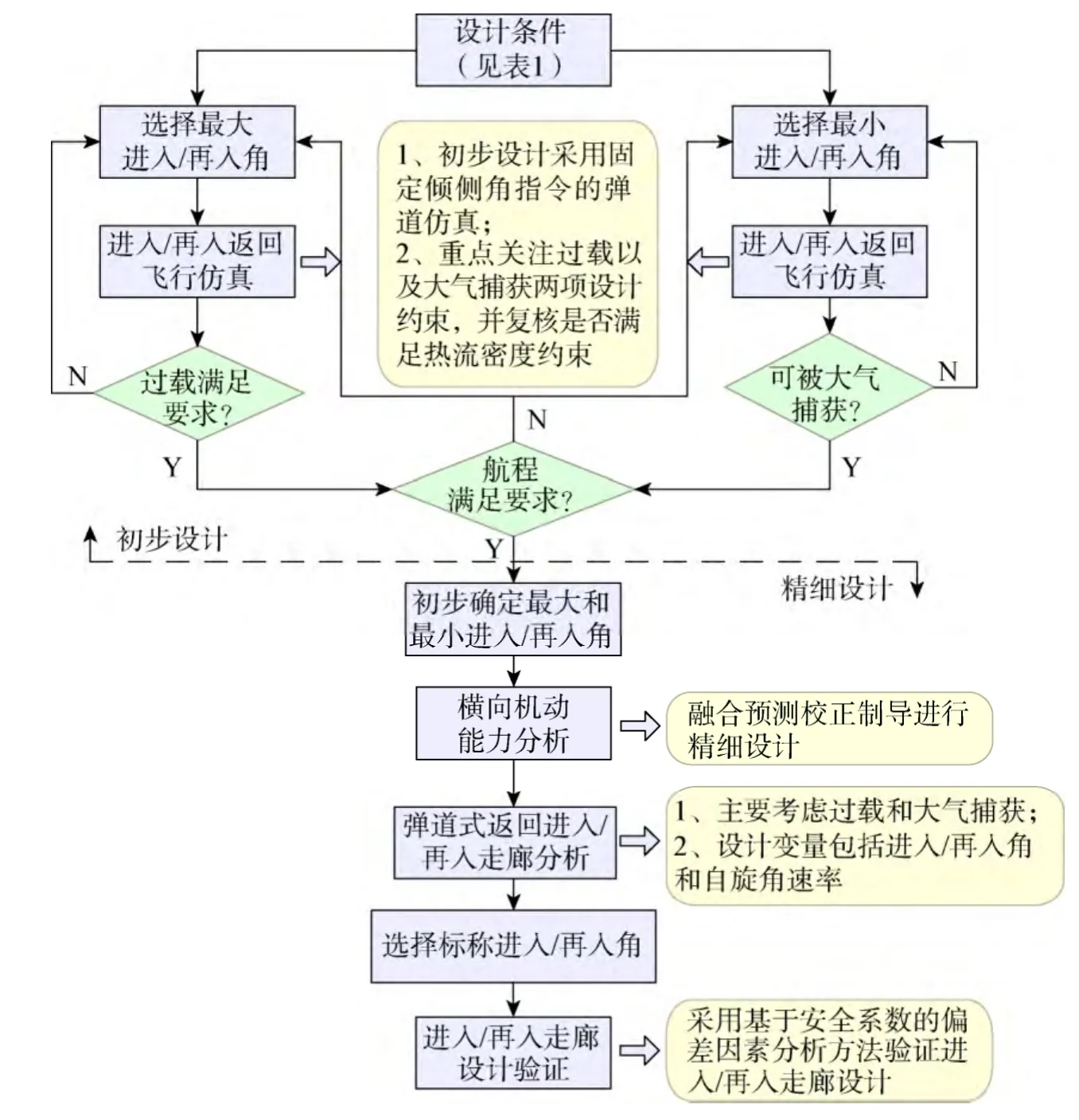
图1 进入/再入走廊的基本设计方法流程Fig. 1 Basic design method for entry/reentry corridor

表2 进入/再入走廊的设计约束Tab.2 Design constraints of entry/reentry corridor

设计过程中固定倾侧角为常值，通过四自由度飞行仿真，确定满足过载约束的最大进入/再入角θmax（对应倾侧角为常值 0°，即全升力向上），以及满足大气捕获的最小进入/再入角 θmin（对应倾侧角为常值180°，即全升力向下）。进一步，对于在[θmax, θmin]范围内的不同进入/再入角θ，采用调整常值倾侧角的方法，分析不同常值倾侧角对应的再入航程，并根据再入航程指标要求，缩小进入/再入角范围至[θmax1, θmin1]，作为初步选定的进入/再入走廊。

（2）精细设计

根据初步选定的进入/再入走廊 [θmax1, θmin1]开展精细设计工作，融合预测校正制导算法，重点分析落点精度和横向机动能力。

精细设计基于再入四自由度或六自由度蒙特卡洛打靶仿真进行，融合导航制导与控制算法，在考虑气动、大气密度、再入初始条件、返回舱质量特性、导航制导与控制器件等所有偏差模型的基础上，开展不同飞行模式下的数值仿真。通过蒙特卡洛打靶仿真，获取[θmax1, θmin1]范围内的不同进入/再入角θ对应的再入过载、热流密度、总加热量、落点偏差、横向机动能力、推进剂消耗等性能参数，根据仿真结果和设计约束要求，进一步缩小进入/再入角范围至[θmax2, θmin2]。

对于载人深空探测而言，必须考虑进入/再入过程无法采用升力控制的情况。这时，为保证飞行姿态稳定并进入/再入至指定着陆区，将采用自旋弹道式进入/再入方式。弹道式进入/再入是应急工况，确保航天员安全是第一要务，因此，弹道式进入/再入落点散布大、航程短、横向机动能力差等问题不予考虑，而将仅仅关注返回舱可被大气捕获和过载2项设计约束。满足大气捕获和过载约束的弹道式进入/再入角范围[θmaxb, θminb]位于[θmax2, θmin2]内，但宽度范围往往很小，例如，对载人月地再入返回地球而言，弹道式再入返回的再入角范围一般不大于0.3°。

为了同时满足载人深空探测正常和应急进入/再入飞行，在弹道式进入/再入角范围[θmaxb, θminb]内选择标称进入/再入角θ0。至此，获取了进入/再入走廊[θmax2, θmin2]和标称进入/再入角θ0。

（3）设计验证

完成进入/再入走廊的精细设计后，采用基于安全系数的偏差因素影响分析方法，开展各项偏差及偏差组合对进入/再入走廊宽度的影响分析。开展这项工作一方面是为了获取各项偏差或偏差组合的灵敏度情况，协调或指导相应分系统的设计改进；另一方面，是为了直接计算进入/再入走廊设计裕度，明确进入/再入走廊的可靠性。

以上阐述了载人深空探测进入/再入走廊的设计方法，可以发现精细设计和设计验证是进入/再入走廊设计的关键环节。为开展精细设计，分析获得满足载人深空探测落点精度、过载、热流密度等设计约束的进入/再入走廊，需融合预测校正制导算法进行飞行仿真；同时，为明确进入/再入走廊的设计裕度，必须研究基于安全系数的偏差因素影响分析方法。

2 进入/再入走廊设计的关键技术

2.1 融合预测校正制导的进入/再入高精度飞行仿真

在进入/再入走廊初步设计中，将全程倾侧角制导指令等效为某一常值倾侧角制导指令，并依此初步确定最大和最小进入/再入角。在精细设计中，必须基于制导算法开展高精度飞行仿真，以校核初步设计获得的进入/再入角范围是否能够满足各项设计约束，特别是落点精度要求。

载人深空探测的制导算法分为两类：

1）标称弹道法。该方法在实施任务前设计一条满足落点精度、过载、热流密度等设计约束的标称进入/再入返回弹道，在飞行中根据导航系统输出，实时比对实际弹道与标称弹道的高度、过载、航程等参数偏差，基于参数偏差生成制导指令以实现偏差修正[7-8]，使返回舱始终飞行在标称弹道的附近，满足进入/再入落点精度、过载等要求。例如，“联盟号”飞船便采用该制导方法。

2）预测校正法。该方法不设计标称弹道，而是在飞行过程中根据导航系统输出的位置和速度矢量，由制导系统实时规划从当前位置飞行至指定着陆点的全程倾侧角指令[9-11]。该制导方法与标称制导相比，具有很强的变航程适应能力，无需在航程变化情况下重新设计标称弹道，同时对于长航程飞行而言，其在各项偏差作用下的落点精度明显高于标称弹道法。“阿波罗”飞船、“猎户座”载人飞船、“火星实验室”[12]等深空探测飞行器均采用了预测校正制导算法，以满足飞行任务灵活、应急模式多样、定点着陆精度要求高的技术要求。图2为预测校正制导的基本流程。

图2 预测校正制导算法流程Fig. 2 Flow of predictive-corrective guidance

如图2所示，预测校正制导方法分为预测和校正两个阶段。在预测阶段，根据导航系统输出的位置和速度参数，计算动力学模型中所需的引力、气动力等参数，并进行飞行仿真，预测按照当前倾侧角规划曲线飞行至弹道终端时的落点位置。在校正阶段，计算预测阶段获取的预测落点位置与理论落点的航程偏差，并根据航程偏差调整倾侧角规划曲线，例如，若预测落点位置远于理论落点，则增大倾侧角、减小升力、压低进入/再入弹道；反之，若预测落点位置近于理论落点，则减小倾侧角。获取倾侧角指令后，由控制系统调整返回舱在修正后的倾侧角下飞行。

综上所述，在载人深空探测进入/再入走廊设计中，采用预测校正法以适应飞行任务多样、应急模式多而引起的航程大范围可变问题，同时，确保长航程下高精度进入/再入着陆。标称弹道法由于设计弹道单一或固化、长航程下落点精度低而难以适应载人深空探测进入/再入走廊的设计。

2.2 偏差因素影响分析

进入/再入走廊宽度的大小与进入/再入飞行各项偏差密切相关，当各项偏差的取值范围变化后，相应的进入/再入走廊也将发生变化。因此，掌握各项偏差对进入/再入走廊的影响至关重要，一方面可以指导返回舱各相关系统的优化设计，另一方面可以获取进入/再入走廊设计裕度，明确进入/再入走廊的可靠性[1]。本文采用基于安全系数的偏差因素影响分析方法，实现多种偏差因素同时作用及各项偏差独立作用时的影响分析。

2.2.1 基本概念

（1）安全系数

返回舱进入/再入过程中的各项偏差均在指定变化范围内，可通过概率模型加以描述。安全系数是指在确定进入/再入走廊[θmax2, θmin2]后，进一步放大1项或各项偏差的变化范围，而不需要改变进入/再入走廊或标称再入角设计值时对应的偏差变化范围最大放大倍数。

例如，某返回舱的进入/再入走廊为[θmaxs, θmins]，某项偏差概率模型为[–10%,+10%]的均匀分布，那么，安全系数FS=1.2即指偏差变化范围放大至[–12%,+12%]，相应进入/再入走廊仍为[θmaxs, θmins]；当偏差变化范围放大倍数大于1.2，进入/再入走廊不再是为[θmaxs, θmins]，而必须做出缩窄调整。

（2）安全系数一致分离点

按相同幅度hf逐步提高所有偏差项的放大倍数Z，并通过蒙特卡洛仿真评估进入/再入走廊内的飞行是否满足各项设计约束。当不满足设计约束时，对应的放大倍数Z减去hf，即为安全系数一致分离点FSU。该点表征各项偏差同时放大情况下，各项偏差同时放大的允许最大边界。

例如，某返回舱进入/再入走廊为[θmaxs, θmins]、安全系数一致分离点FSU为 1.3，意味着当所有偏差范围同时放大1.3倍情况下，进入/再入走廊仍为[θmaxs, θmins]；当同时放大倍数大于1.3倍后，进入/再入走廊不再是为[θmaxs, θmins]，而必须做出缩窄调整。

2.2.2 偏差因素影响分析方法

结合安全系数一致分离点和安全系数的定义，给出基于安全系数的偏差因素影响分析方法。首先，确定进入/再入走廊对应的安全系数一致分离点FSU；而后，以FSU作为初值，逐个放大单项偏差的偏差变化范围，进而逐一确定偏差i的安全系数FSi。容易知道，FSU为所有偏差同时放大情况下的进入/再入走廊设计裕度，而FSi既描述单一偏差允许变化的最大边界，也描述了单一偏差放大情况下的进入/再入走廊设计裕度。基于安全系数的偏差影响分析结果示意如图3所示。

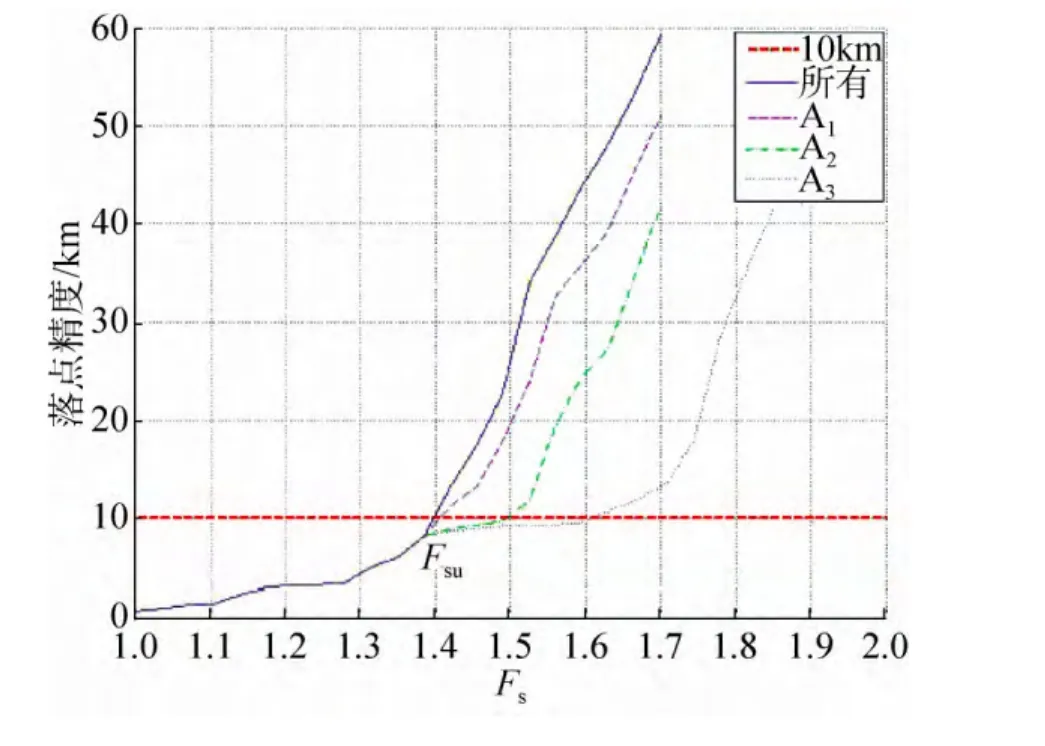
图3 基于安全系数的偏差因素影响分析结果示意Fig. 3 Factor of safety based on variance analysis results

由图3可见，安全系数一致分离点FSU为1.4，即在进入/再入走廊内，当所有偏差同时放大1.4倍时，落点精度仍满足10km指标要求，当所有偏差同时放大的倍数大于1.4时，落点精度不再满足要求，需重新调整进入/再入走廊，1.4即为所有偏差同时放大情况下的进入/再入走廊设计裕度。另外，偏差A1的安全系数也在1.4附近，并且曲线最为接近所有偏差同时放大情况下的落点精度曲线，说明偏差A1对进入/再入走廊影响最大，单独放大偏差A1的作用几乎与所有偏差同时放大一致。偏差A2和偏差A3安全系数分别是1.5和1.6，说明在所有偏差按照安全系数一致分离点数值放大的基础上，继续放大偏差A2和A3变化范围至1.5倍和1.6倍，落点精度仍满足10km指标要求，不需调整进入/再入走廊，即1.5和1.6为单一偏差放大情况下的进入/再入走廊设计裕度。

需要指出，限于篇幅，仅通过图3示意了在进入/再入走廊内，各项偏差变化对落点精度的影响分析结果，并相应给出了安全系数一致分离点FSU和各项偏差安全系数的关系，明确了进入/再入走廊的设计裕度。事实上，在开展偏差影响分析并确定进入/再入走廊裕度时，需要分析各项偏差对过载、热流密度、总加热量、航程、横向机动能力、推进剂消耗等所有设计约束的影响，综合分析各项偏差对设计约束的影响程度，以相对保守的方式，确定进入/再入走廊的安全系数一致分离点和各项偏差的安全系数，最终作为进入/再入走廊的设计裕度。

3 仿真验证

本节利用前述章节提出的载人深空探测进入/再入走廊设计方法，以载人月地再入返回地球为例，仿真验证所提方法的有效性。

3.1 设计条件和约束

返回舱再入返回设计条件参照“阿波罗”飞船相关的参数[3]，仿真中主要设计条件和考虑的设计约束分别如表3所示。其中，偏差因素考虑对再入走廊设计影响最大的3项，分别为升力系数、阻力系数和大气密度；考虑到热流密度相较于过载而言是弱约束，因此，设计约束仅考虑系统总体设计最为关注的过载峰值和落点精度。为了在不影响再入走廊设计验证的基础上简化仿真，航程设定为2 300km固定航程。此外，蒙特卡洛打靶组数设定为100组。

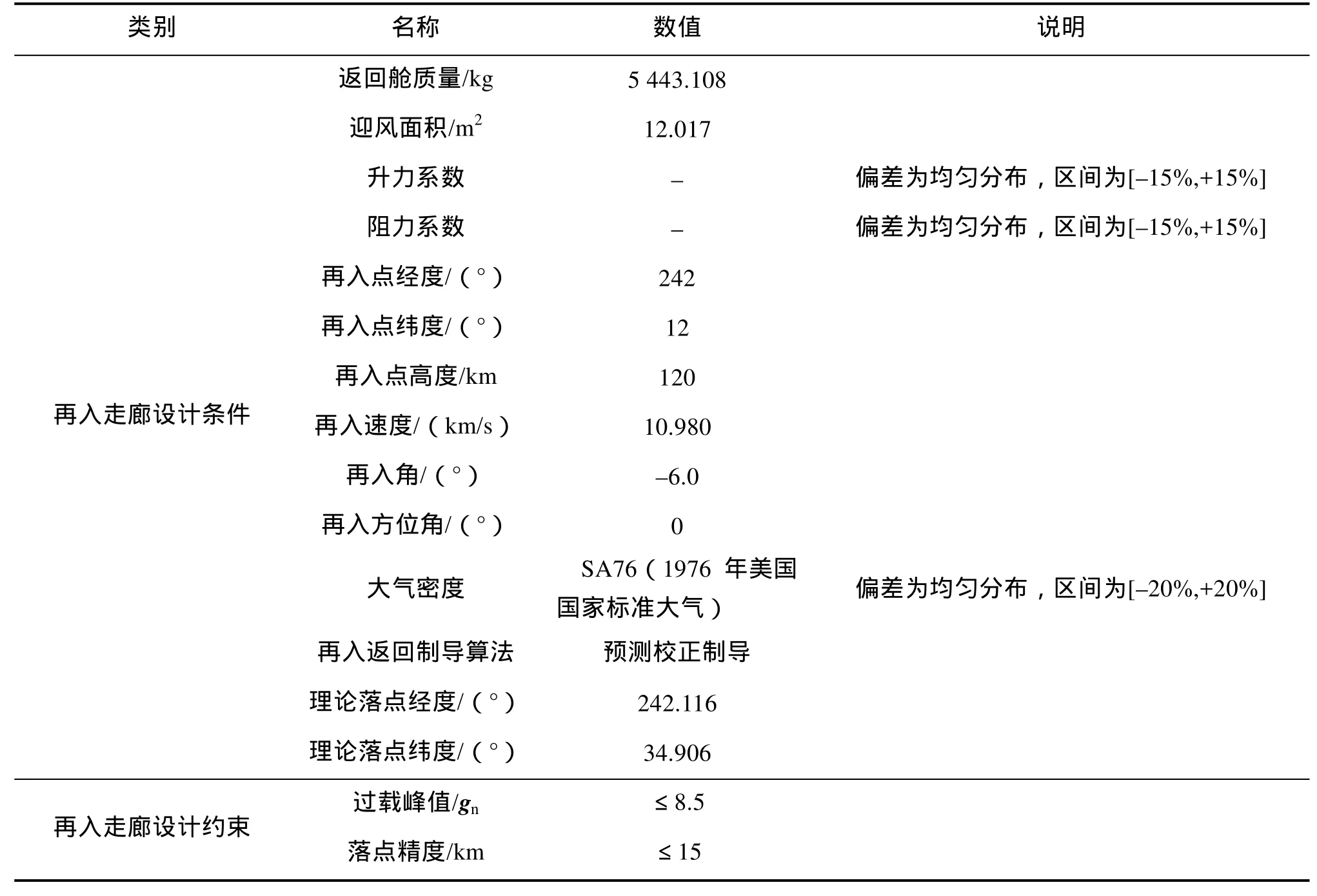
表3 再入走廊设计条件和设计约束Tab.3 Design conditions and constraints of reentry corridor

3.2 再入走廊仿真设计

按照本文提出的再入走廊初步设计和精细设计方法，通过数值仿真，获得了满足设计约束的再入走廊为[–5.4°, –6.6°]（相应的弹道式返回再入走廊[–5.9°, –6.1°]）。

融合预测校正制导算法，标称情况下，再入走廊内的过载峰值不大于 7gn，过载曲线如图 4和图 5所示；偏差情况下，再入走廊内的过载峰值不大于7.7gn、落点精度优于5km，过载和落点散布的结果如图6~图9所示。由仿真曲线可见，设计获得的再入走廊满足过载峰值和落点精度设计约束。

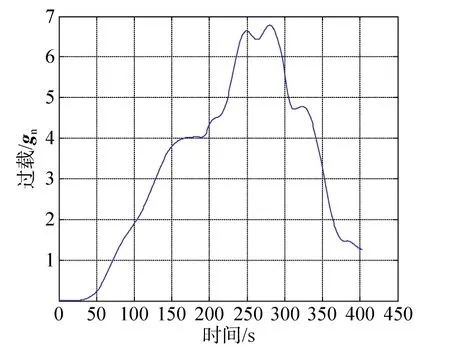
图4 再入角为–5.4°时的过载曲线（标称）Fig. 4 Nominal load (flight path angle is –5.4°)

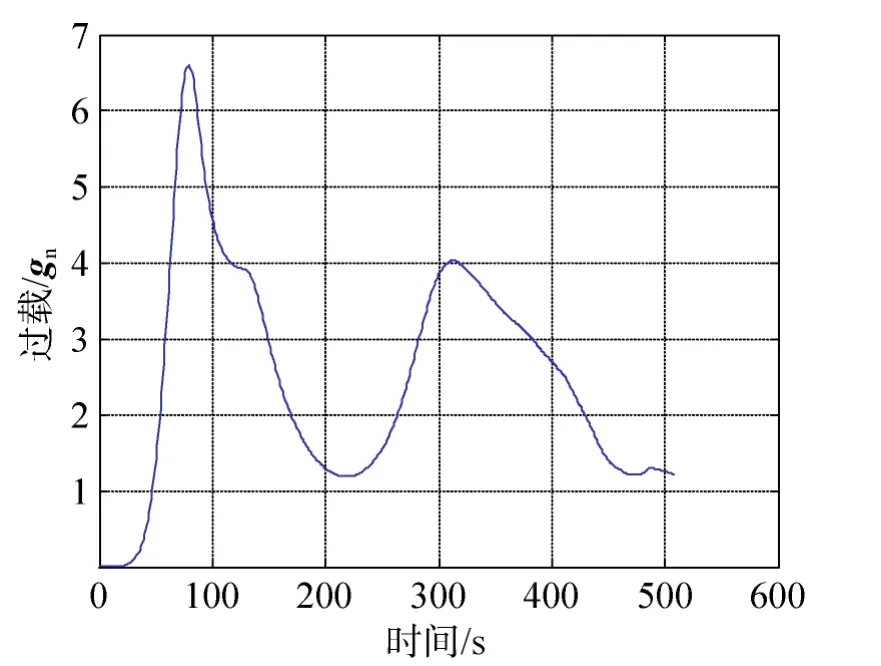
图5 再入角为–6.6°时的过载曲线（标称）Fig. 5 Nominal load (flight path angle is –6.6°)

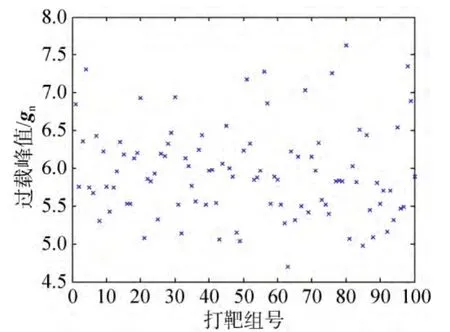
图6 再入角为–5.4°时的过载峰值（偏差）Fig.6 Peak loads (flight path angle is –5.4°)

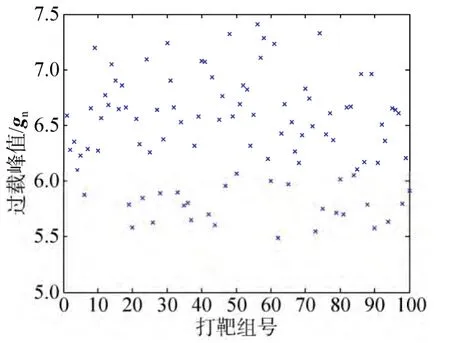
图7 再入角为–6.6°时的过载峰值（偏差）Fig.7 Peak loads (flight path angle is –6.6°)

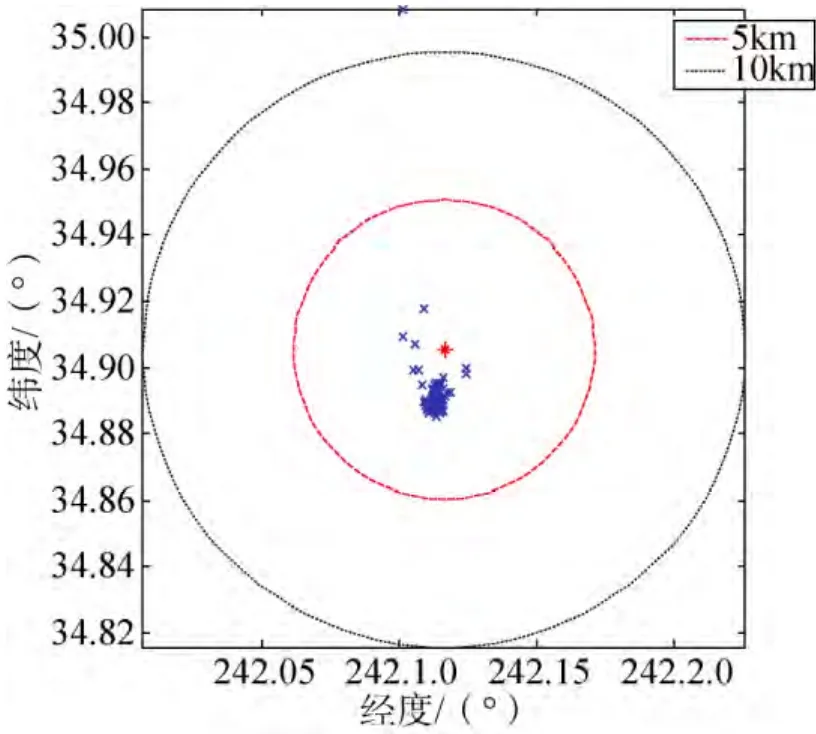
图8 再入角为–5.4°时的落点散布（偏差）Fig.8 Footprints (flight path angle is –5.4°)

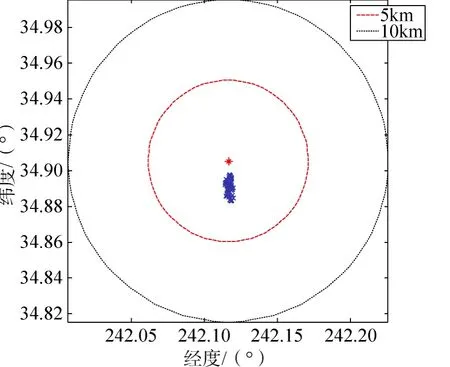
图9 再入角为–6.6°时的落点散布（偏差）Fig.9 Footprints (flight path angle is –6.6°)

3.3 再入走廊验证

在完成再入走廊设计后，采用基于安全系数的偏差因素影响分析方法，开展升力系数偏差、阻力系数偏差和大气密度偏差对再入走廊的影响分析。探讨升力系数偏差、阻力系数偏差和大气密度偏差对过载峰值和落点精度的影响，并计算再入走廊的设计裕度。图10至图11为上述偏差对过载峰值以及落点精度的影响分析结果。

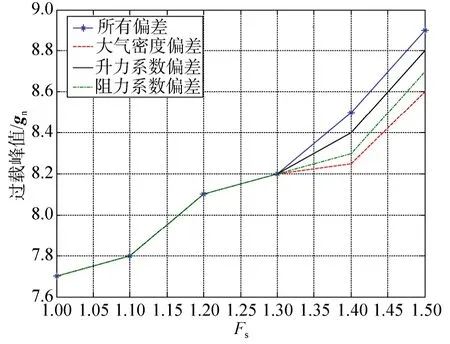
图10 基于安全系数的偏差因素影响分析（对过载峰值的影响）Fig.10 Analysis of variance based on the concept of factor of safety (for peak load)

图11 基于安全系数的偏差因素影响分析（对落点散布的影响）Fig.11 Analysis of variance based on the concept of factor of safety (for footprints)

由图10~11可得如下结论：

1）升力系数偏差、阻力系数偏差和大气密度偏差对再入走廊的影响逐渐减弱。

2）对于过载峰值而言，再入走廊的安全系数一致分离点为1.4；对于落点散布而言，再入走廊的安全系数一致分离点为1.3；按照保守数值考虑，取定再入走廊的安全系数一致分离点为1.3，即再入走廊对所有偏差同时放大的设计裕度是30%。

3）对于过载峰值而言，大气密度偏差的安全系数为1.4；对于落点散布而言，大气密度偏差的安全系数为1.4，综合取定大气密度偏差的安全系数为1.4，即在安全系数一致分离点基础上，大气密度偏差可继续放大1.4倍，相应的设计裕度是40%；按照相同方法分析，升力系数偏差和阻力系数偏差的安全系数均为1.3。

4 结束语

本文提出载人深空探测进入/再入走廊的数值仿真设计方法，系统梳理了进入/再入走廊设计中的设计条件与设计约束，给出了进入/再入走廊的设计流程。在进入/再入走廊仿真设计中，融合了预测校正制导律，以准确反映不同进入/再入飞行条件下的落点散布，确保进入/再入走廊设计的可行性；同时，采用基于安全系数的偏差因素影响分析方法，通过计算安全系数一致分离点和各项偏差的安全系数，直接反映进入/再入走廊的设计裕度，确保了进入/再入走廊设计的可靠性。最后，以载人月地再入返回为例，具体阐明了再入走廊的设计方法，通过数学仿真验证设计方法的有效性，给出了再入走廊的设计结果和偏差影响分析结果。本文结果可为载人深空探测进入/再入走廊设计及进入/再入返回总体设计提供技术参考。

References)

[1] Jeremy R R. Orion Entry Flight Corridor Analysis[R]. AIAA 2008-7153, 2008.

[2] 贾世锦. 载人登月返回再入有关问题初步研究[J]. 航天返回与遥感, 2011, 32(2):18-25. JIA Shijin.Preliminary Study on the Return and Re-entry of Manned Lunar Landing[J].Spacecraft Recovery & Remote Sensing,2011,32(2):18-25.(in Chinese)

[3] Schneider L, Heath D W, Griffith D J. Entry Corridor Definition and SM-RCS Deorbit Requirements for Apollo Block 1 Earth Orbit Missions - Project Apollo[R]. NASA TMX -64486, 1970.

[4] 沈红新, 彭祺擘, 李海阳. 载人登月再入段应急策略仿真分析[J]. 载人航天, 2012, 18(4):52-57. SHEN Hongxin, PENG Qibo, LI Haiyang. Simulation Analysis of Reentry Emergency Strategy for Manned Lunar-landing Mission[J]. Manned Spaceflight, 2012, 18(4):52-57. (in Chinese)

[5] 闵学龙, 潘腾, 郭海林. 再入参数调整对登月航天器返回再入特性的影响[J]. 航天返回与遥感, 2010, 31(4):15-20. MIN xue Long, PAN Teng, GUO Hailin. Reentry Parameters Change Influences on Manned Lunar Mission Capsule Reentry Characters[J]. Spacecraft Recovery & Remote Sensing, 2010, 31(4):15-20. (in Chinese)

[6] Tigges M A, Bihari B D. Orion Capsule Handling Qualities for Atmospheric Entry[R]. AIAA 2011-6264, 2011.

[7] Tian B, Zong Q. Optimal Guidance for Reentry Vehicles Based on Indirect Legendre Pseudospectral Method[J]. Acta Astronautica, 2011, 68(7): 1176-1184.

[8] Lu P. Entry Guidance and Trajectory Control for Reusable Launch Vehicle[J]. Journal of Guidance, Control, and Dynamics, 1997, 20(1): 143-149.

[9] Lu P. Predictor-corrector Entry Guidance for Low-lifting Vehicles[J]. Journal of Guidance, Control & Dynamics, 2008, 31(4):1067-1075.

[10] Rea J, Putnam Z. A Comparison of Two Orion Skip Entry Guidance Algorithms[R]. AIAA 2007-6424, 2007.

[11] Strahan A, Loe G, Seiler P. Orion Entry Flight Control Stability and Performance[R]. AIAA 2007-6429, 2007.

[12] Braun R D, Manning R M. Mars Exploration Entry, Descent, and Landing Challenges[J]. Journal of Spacecraft and Rockets, 2007, 44(2): 310-323.