重型柴油机空气滤清器技术状况监测方法
2014-03-11赵永东赵文柱王宪成
赵永东,赵文柱,王宪成,和 穆
(装甲兵工程学院机械工程系,北京100072)
空气滤清器的主要作用是滤清进入气缸的空气,除去空气中所携带的尘土等杂质,减轻发动机内各零件之间的磨损。随着空气滤清器内尘土的增加,进气阻力会增大,甚至发生空气滤清器击穿,将严重影响发动机正常工作。因此,必须定期对空气滤清器进行保养。目前,对某重型柴油机空气滤清器技术状况的检测仅通过阻力指示器的报警实现。测试时,原位稳定发动机转速2 000 r/min,当空气滤清器进气阻力达到(8±0.6)kPa时,信号灯亮,指示器报警。但是该方法只适用于原位测试,在车辆行驶过程中无法有效地监测空气滤清器的技术状况。根据某地实际调研情况可知:大多数空气滤清器击穿都是由于不能实时监测其使用情况,在行驶过程中发生的。
在车辆行驶过程中对空气滤清器进行监测可以实时了解其技术状况,防止因无法预知空气滤清器击穿而造成的严重事故。为此,笔者通过分析空气滤清器内部气体流动过程,选用经验公式计算各部件压降损失,推导出了空气滤清器的技术状况监测数学模型。通过台架和实车试验,验证了该模型能够准确地反映空气滤清器的使用情况,可实时监测空气滤清器的技术状况,为其及时保养提供依据。
1 空气滤清器监测模型建立
1.1 气体流动过程假设
空气滤清器内部流动为气固两相流动,但是分析和计算两相流动问题比较复杂,为了方便计算,将空气滤清器内部流动简化为空气的单相流动,对内部气体作如下假设[1-3]:1)空气中尘土对空气流动的影响忽略不计,空气运动不受尘土的影响;2)空气流动过程为定常流动;3)忽略温度的影响,认为整个流动过程为等温过程;4)二级滤清器(金属滤网)采用多孔介质模型,在流动过程中金属滤网完全固定,空气滤清器内部构件为绝对刚体。
1.2 等效流通截面积模型公式推导
某重型柴油机空气滤清器主要由一级滤清器(旋风筒)、二级滤清器(滤尘丝盒)、盖板、头部等部分组成,其结构简化模型图1所示。
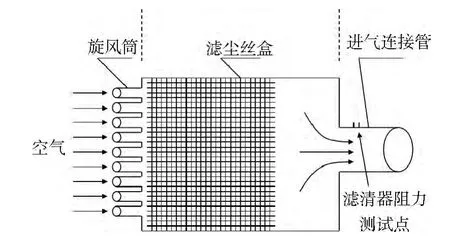
图1 空气滤清器结构简化模型
忽略空气滤清器进气口至旋风筒的损失,即整个空气滤清器的压降ΔP由旋风筒压降ΔP1、滤网压降ΔP2和进气连接管处局部阻力损失ΔP3组成:
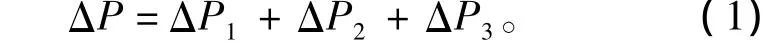
1.2.1 旋风筒压降计算模型
轴向旋风筒主要由中心管、旋流叶片、导流管组成。在旋流叶片的导流作用下,空气沿叶片高速旋转运动,在超出导流管端口时改变方向,中心导流管急速逆向流动。在离心力和惯性力的作用下,大颗粒的尘土被收集到集尘箱,较清洁的空气进入二级滤清器。
旋风筒的压力损失主要包括旋风筒形状压力损失、气体流动摩擦损失和内部漩涡耗散损失[4-5]。在旋风筒压降计算方面,国外学者做了大量的研究,根
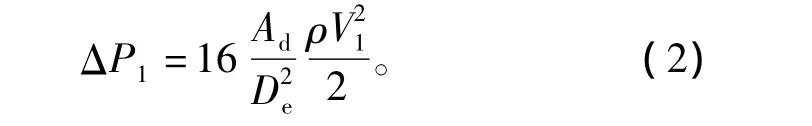
式中:Ad为旋风筒进气口面积(m2);De为旋风筒出气口直径(m);ρ为气体密度(kg/m3);V1为进气口气流平均流速(m/s)。
1.2.2 金属滤网压降计算模型
金属滤网由24层粗滤网和20层细滤网叠加而成,网孔尺度一般是丝网直径的几十倍。为了计算压降,必须简化模型。在实际计算中,将金属滤网区域等效为多孔介质模型,根据Darcy-Stoke方程[7],可得据试验数据和实践经验提出了适用于旋风筒压降的经验公式,本文采用Lapple建立的计算式[6]:
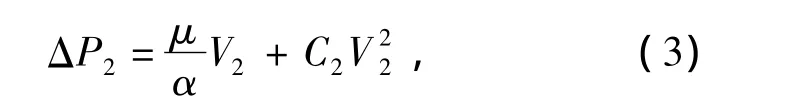
其中
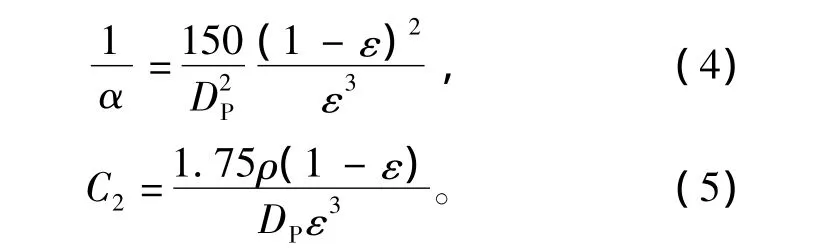
式中:1/α为黏性阻力系数;C2为惯性阻力系数;μ为气体动力黏度(Pa·s);V2为通过滤芯的气流流速(m/s);DP为滤芯孔隙平均直径(m);ε为滤芯孔隙率。其中,DP可以从材质报告中得到,ε指材料内空孔的体积与总体积之比。对于油浴式空气滤清器,一般丝网直径不大于0.30 mm,孔隙率不大于97%[8]。
1.2.3 进气连接管处局部阻力损失
清洁空气由空气滤清器到进气连接管时,流通面积突然缩小,流动状态发生急剧变化,造成了能量的损失,根据工程流体力学知识,局部损失表示为[9]

其中
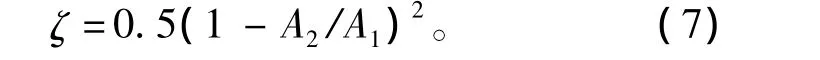
式中:ζ为局部阻力系数;V3为空气滤清器出口处流速(m/s);g为重力加速度(m/s2);A1为空气滤清器截面积(m2);A2为进气连接管截面积(m2)。
1.2.4 空气滤清器等效流通截面积数学模型
气体质量流量为

气体体积流量为

式中:A为气体流通截面积(m2);V为气体流速(m/s)。
根据质量守恒定律,联立式(1)、(2)、(6)、
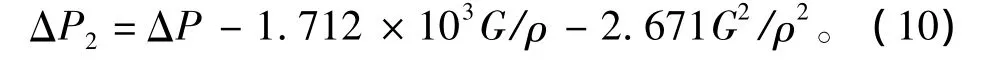
(8),代入滤清器结构参数,可得将式(10)代入到式(3)中,联立式(4)、(5)、(9)可得到空气滤清器流通截面积:
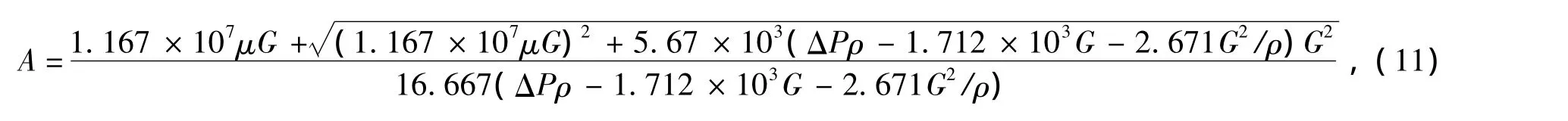

式中:Aφ为空气滤清器等效流通截面积(m2);μφ=,为空气滤清器流量系数。
气体动力黏度根据经验公式近似计算[9]:
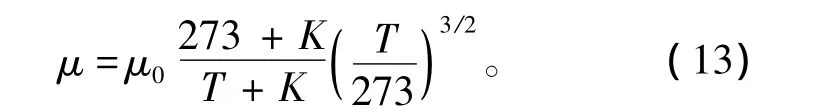
式中:μ0为气体在0℃时的动力黏度(空气为1.71×10-3Pa·s);T为气体热力学温度(K);K为依气体种类而定的系数(空气为111)。
气体密度计算公式:
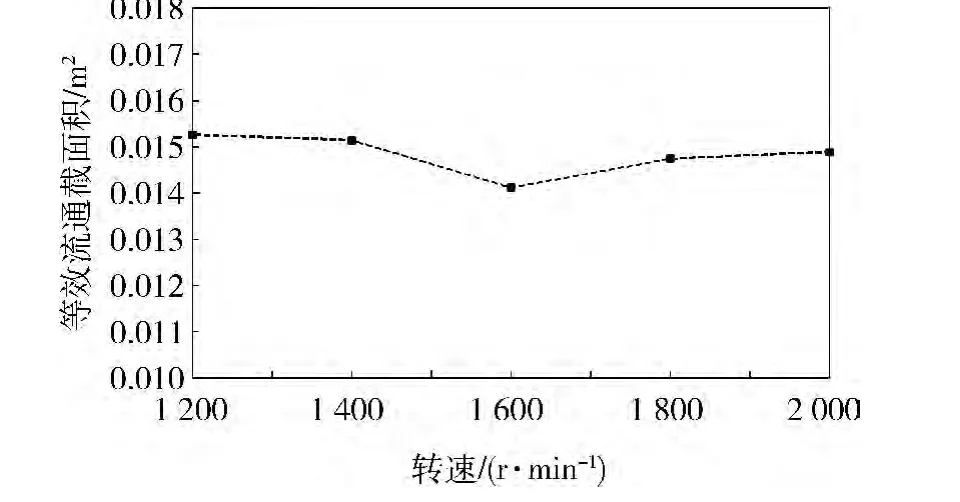
图2 不同转速下等效流通截面积
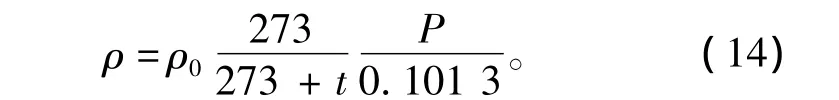
式中:P 为气体压强(MPa);ρ0=1.293 kg/m3,为标准大气压0℃时空气密度;t为气体温度(℃)。
目前,该型柴油机空气滤清器并没有高原条件下进气阻力阈值的规定,但是根据数学模型的定义,无论在高原地区还是平原地区,等效流通截面积的值是不变的。因此,根据某型柴油机《空气滤清器使用维护说明书》的规范,平原地区标定工况下进气流量达到最大值1.24 kg/s时,滤清器阻力最大值为 13.72 kPa,最小值为 3.63 kPa,由此,可以计算出该空气滤清器等效流通截面积的极限值分别为0.008 9 m2和 0.031 6 m2。器的等效流通截面积,5组数据的标准差为4.49×10-4,误差为4.82%,通过数值可以看出:不同转速下的等效流通截面积变化不大,且都在极限值范围之内。由此证明了推导出的空气滤清器等效流通截面积模型稳定性较好,适用于高原地区。
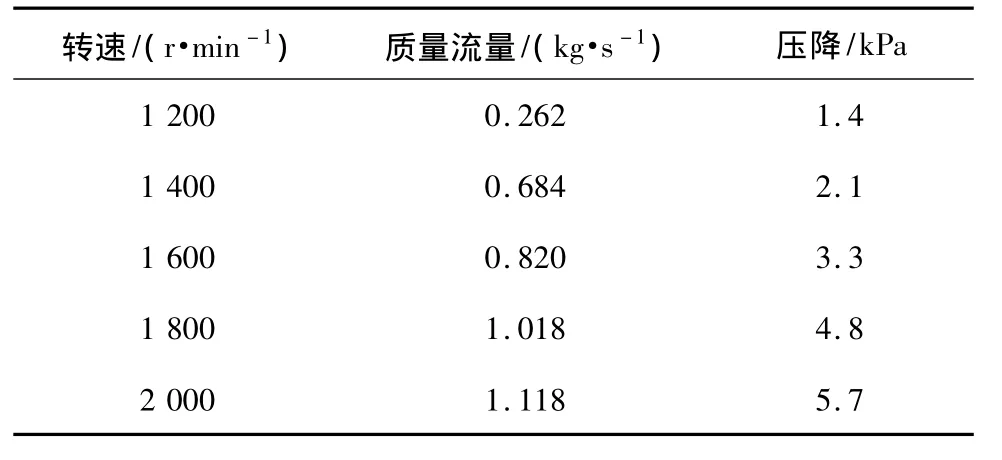
表1 台架试验测试数据
2 台架试验验证
2.2 模型单调性验证
空气滤清器的等效流通截面积在实体上进行测量比较困难,难以得到其真实值。通过开展台架试验,对模型的稳定性和单调性进行检验,从而验证模型的正确性。
2.1 模型稳定性验证
试验在车辆动力性能实验室进行,环境条件:大气压力88.9 kPa;大气温度34℃。测取不同转速下进入到发动机的空气质量流量以及滤清器的压降,通过式(12)计算滤清器的等效流通截面积,计算结果如图2所示。表1为台架试验测试数据。
由图1可见:空气滤清器等效流通截面积不随转速升高而增大,不同工况下其数值变化不大。取5次不同工况下的平均值0.014 m2为该空气滤清
在空气滤清器试验台架上进行空气滤清器容尘试验,试验选用国际标准(ISO)规定的标准试验粉尘。试验环境温度20℃,大气压力86.65 kPa。试验时调节进气流量为1.24 kg/s,按照含尘浓度2 g/m3对被试验的空气滤清器进行均匀连续加灰尘10 min,然后记录下进气阻力,每10 min做一组记录,直至进气阻力达到13.72 kPa左右为止。图3为进气阻力随时间变化的曲线,可以看出:随着灰尘的不断增加,进气阻力不断增大,由6.86 kPa增加到13.83 kPa。图4为根据模型计算出的等效流通截面积随时间变化的曲线,可以看出:空气滤清器等效流通截面积随时间单调下降,在440 min内由0.015 4 m2减小到 0.009 2 m2,减小了 0.006 2 m2,整个容尘试验中等效流通截面积都在所计算的极限值范围之内变化,进一步验证了模型的正确性。
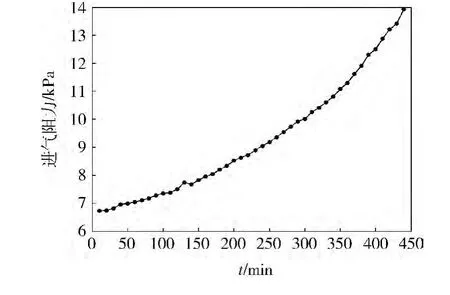
图3 进气阻力随时间变化的曲线
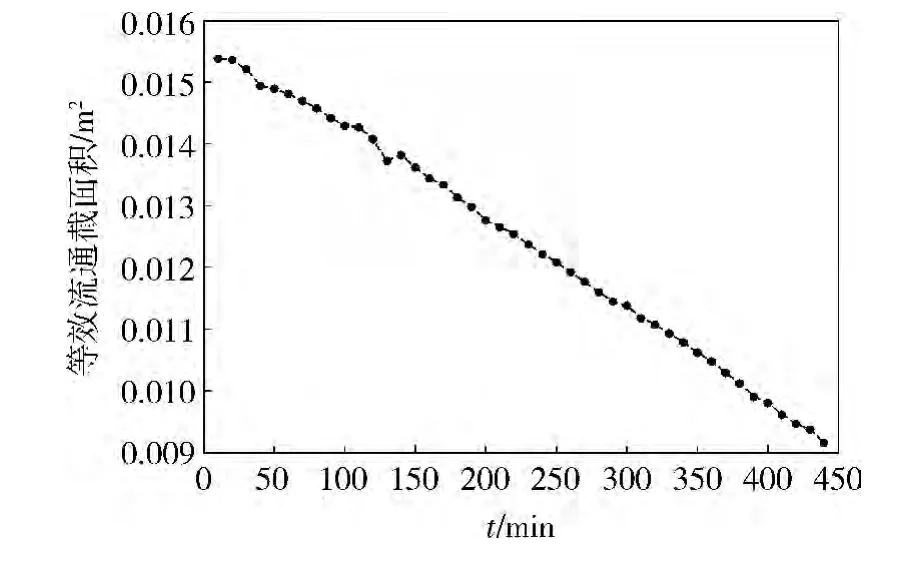
图4 等效流通截面积随时间变化的曲线
3 实车试验
3.1 实车原位空转试验
在北京某地区对该型柴油机进行实车原位空转试验,环境温度20℃,大气压力100 kPa。试验时,稳定发动机转速在 600~2 000 r/min,每升高200 r/min测试1次,分别测量大气压力、大气温度、滤清器后压力、压气机前压力、压气机前温度等参数。进气流量参照文献[10]中的方法计算,得出每个工况点下的等效流通截面积如图5所示,计算得出其平均值为0.012 8 m2,相对平均值最大波动为0.000 6 m2,误差为 4.98%。
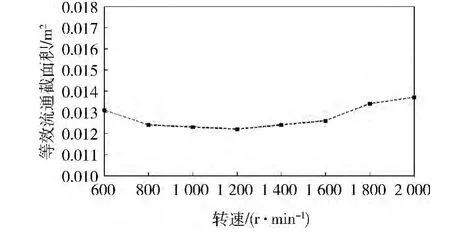
图5 不同转速下实车原位试验等效流通截面积
3.2 实车跑车试验
在新疆叶城某训练场进行实车跑车试验,场地含尘量为2.0 ~7.0 g/m3,环境温度10 ℃,大气压力86.82 kPa。试验使用同一台车连续行驶3 h,每行驶1 h后进行原位测试。测试时,稳定转速在600~2 000 r/min,每升高200 r/min测试1次。行驶不同时间后,原位空转不同转速下空气滤清器压降如图6所示。从图6中可知:原位空转相同转速下,行驶时间越长,空气滤清器压降越大。不同行驶时间后空气滤清器等效流通截面积如图7所示,对每次计算的不同转速下的值取平均,得到3次等效流通截面积的平均值。随着跑车时间的增长,空气滤清器等效流通截面积单调减小,平均值由0.012 7 m2减小到 0.009 9 m2。
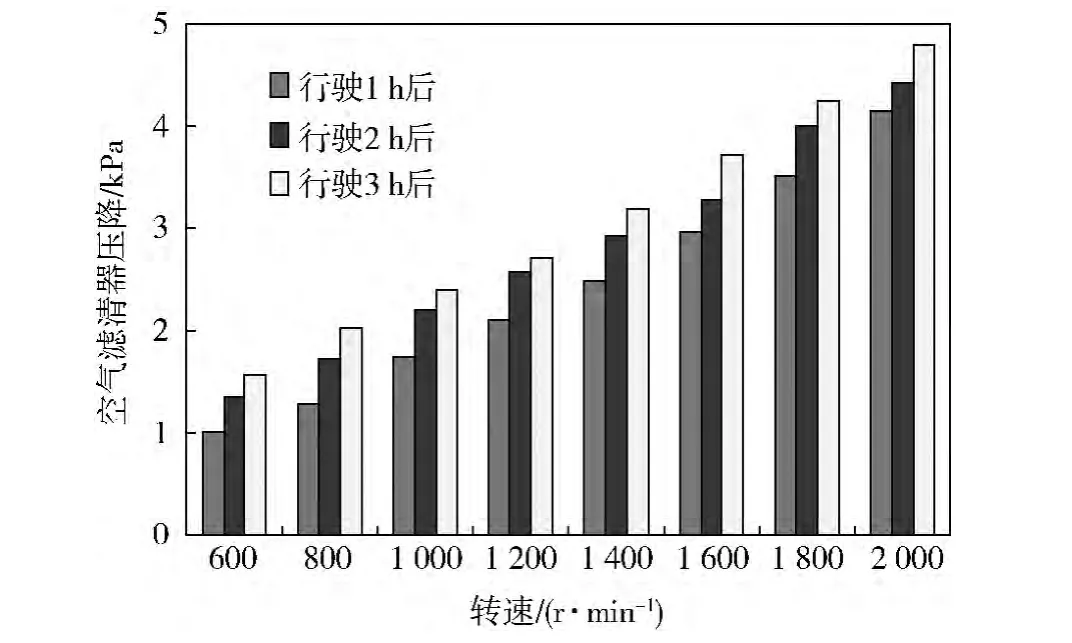
图6 不同行驶时间后原位空转空气滤清器压降
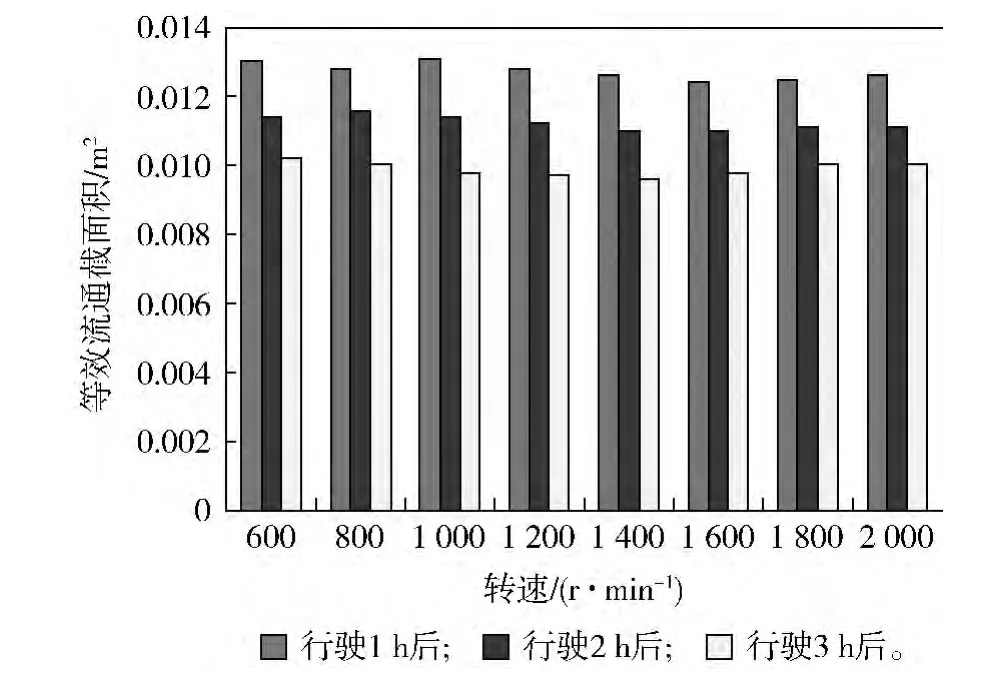
图7 不同行驶时间后空气滤清器等效流通截面积
在西藏某场地进行实车在线监测试验,场地内有土岭、沟壕等路障,路面浮土高度约20 cm,环境温度28℃,大气压力59.6 kPa。试验使用同一台车连续行驶约40 min。行驶过程中进气流量和进气阻力随时间的变化曲线分别如图8、9所示,可以看出:由于行驶过程中工况、负荷的不同,进气流量和进气阻力呈现上下波动的情况,进气流量最大值为0.58 kg/s,最小值为 0.43 kg/s,进气阻力最大值为 1.845 kPa,最小值为1.020 kPa。根据推导出的空气滤清器监测模型,求出等效流通截面积,其实测值与拟合值随时间变化曲线对比如图10所示。由于实际行驶中工况不稳定以及振动等其他因素的影响,等效流通截面积存在一定波动。由拟合曲线可知:随着行驶时间的增长,等效流通截面积呈现不断下降的趋势,从0.017 m2减小到0.014 m2,约减少了0.003 m2。由此验证了该模型实车监测的可行性和准确性。
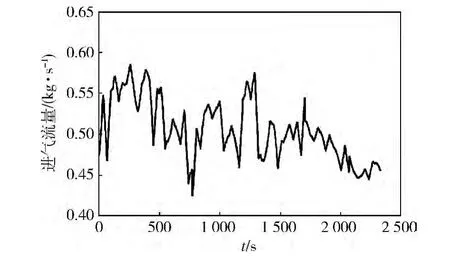
图8 进气流量随时间的变化曲线
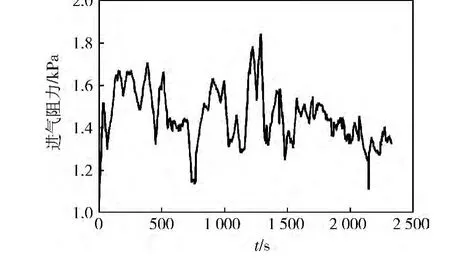
图9 进气阻力随时间的变化曲线
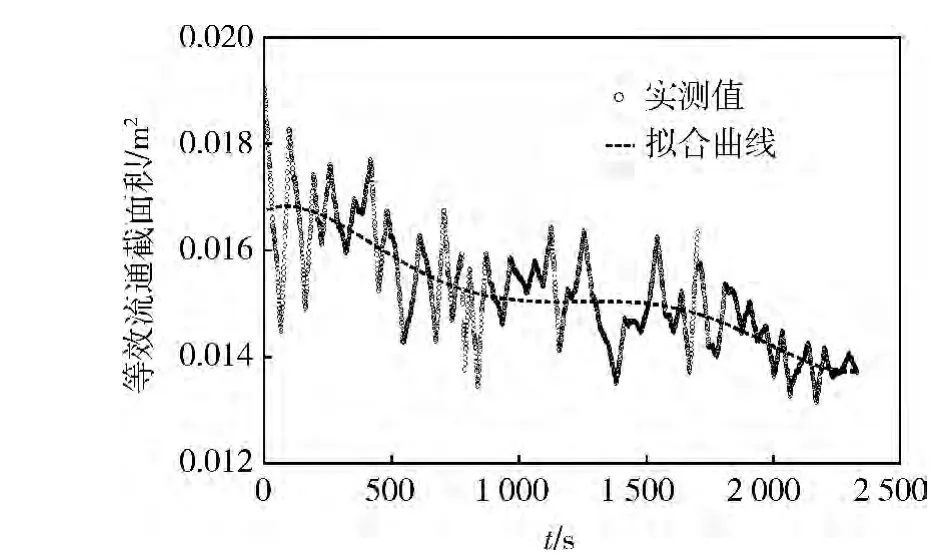
图10 等效流通截面积实测值与拟合值随时间的变化曲线对比
4 结论
本文通过简化空气滤清器物理模型,运用流体力学相关知识,参考经验公式,建立了空气滤清器等效流通截面积数学模型。通过台架试验验证了该模型具有较好的稳定性、准确性以及单调性,能够反映出空气滤清器技术状况的优劣程度。在不同海拔开展了实车试验,结果表明:该模型同时适用于平原地区和高原地区,可以用于原位状态监测,也可以用于实车在线监测。模型的运用对及时清洗空气滤清器、合理安排保养周期具有重要意义,能够有效预防因进气阻力增大造成工作恶化以及因空气滤清器击穿造成磨损加剧等现象的发生。
[1] 王伟,王仁人,张良.基于CFD的内燃机空气滤清器内气固两相流数值模拟[J].德州学院学报,2010,26(2):77-81.
[2] 李佳,刘震涛,刘忠民,等.空气滤清器流动过程仿真与试验分析[J].浙江大学学报,2012,46(2):327-332.
[3] 张慧,富旭光.空气滤清器的CFD分析及空气流动性优化[J].流动传动与控制,2012,46(3):34-37.
[4] 王德耕.旋风分离器速度分布指数及压降计算通用模型[J].化学工程,1998,26(1):44-48.
[5] 吴克明,潘留明.旋风分离器压力损失的数学模型及在设计中的应用[J].化工环保,2005,25(2):156-160.
[6] Shepperd C B,Lapple C E.Flow Patter and Pressure Drop in Cyclone Dust Collectors[J].Ind End Chem,1939,31(8):972-984.
[7] 李伟,王珂.基于CFD的滤材仿真参数研究[J].研究与开发,2011(10):85-88.
[8] 霍玉荣.空气滤清器的设计与计算[J].内燃机与配件,2011(7):9-12.
[9] 归柯庭,汪军,王秋颖.工程流体力学[M].北京:科学出版社,2003:15-16.
[10] 和穆.高原坦克动力装置状态监测与寿命预测方法研究[D].北京:装甲兵工程学院,2012.
