双曲调频信号测速测距方法研究
2014-03-10庞玉红严琪王世闯
庞玉红 严琪 王世闯
(第七一五研究所,杭州,310023)
双曲调频信号测速测距方法研究
庞玉红 严琪 王世闯
(第七一五研究所,杭州,310023)
在分析双曲调频信号的多普勒不变性和匹配滤波算法特性的基础上,提出使用连续发射的一组正反双曲调频信号对目标的速度和距离进行估计的方法,并对该方法进行了仿真分析。通过性能分析发现,该方法测速和测距误差小、精度高,能够较好地获取目标的距离和速度信息,具有工程实用价值。
双曲调频;测速;测距;多普勒不变性
声呐是海洋中探测潜艇的最重要的手段。随着潜艇减震降噪技术的发展,潜艇辐射声源级正以每年1 dB的速度降低,被动探潜的性能受到了严重约束,故主动声呐在探潜中的地位变得愈加重要。主动声呐探测中,宽带信号比窄带信号更具优势。宽带信号可激发更多目标特征,其回波信号携带更多目标信息,且混响背景相关性较弱,因此宽带信号更有利于目标参量的精确估计和检测[1]。
线性调频信号(LFM)在目标速度和距离估计中存在诸多问题,如较大的多普勒频移会导致匹配滤波严重失配,使匹配滤波输出的峰值产生大幅度衰减和主峰展宽,从而影响了主动声呐的探测性能。众所周知,声呐和雷达的回声定位系统借鉴了蝙蝠、海豚等生物的回声定位系统,而这些生物的超声波信号具有相同的波形结构:它们发射的信号都是双曲调频信号(HFM)[2]。从进化论的角度看,这种信号在目标距离速度估计中有优势,因此HFM信号值得深入研究和利用。本文在HFM波形特征的基础上,分析了HFM信号的多普勒不变性和匹配滤波特性,提出了利用两个连续发射的正反HFM信号,进行目标距离和速度的估计方法。
1 双曲调频信号(HFM)
1.1 时间波形

其中,f0为HFM信号的中心频率,T为脉冲宽度。瞬时频率描述了不稳定波形的时间变化性质,定义为
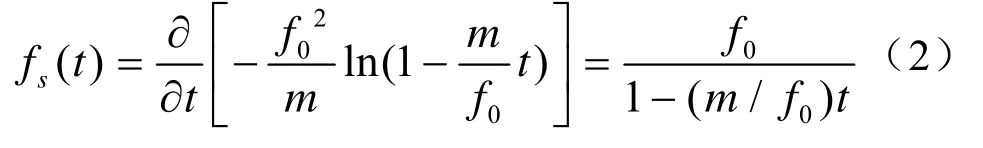
显然,fs(0)=fL,fs(T)=fH。瞬时频率在起始频率fL和截止频率fH之间连续单调,其服从双曲分布,带宽B=fH−fL。如果fH>fL,则HFM信号是调制频率随时间递增的双曲调频(m>0),记为HFM+,反之,调制频率随时间递减(m<0),记为HFM-。
1.2 模糊函数
模糊函数(Ambiguity Function,AF)是波形设计与分析的工具,它可以方便地刻画波形与对应匹配滤波器的特征。
信号s(t)的模糊函数定义为[3]

式中,τ为信号时延,ξ为信号频移。
根据上式绘出HFM信号的模糊函数图,如图1所示。可知HFM信号具有很高的时延分辨力,测距精度较高。但是其多普勒频移分辨力很差,无法用传统的多普勒测速法进行速度的估计。
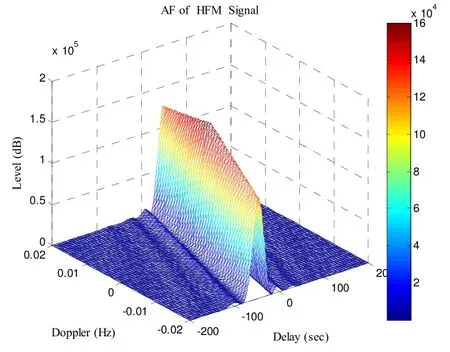
图1 双曲调频信号的模糊函数图
2 测速原理
2.1 多普勒不变性[4]
当目标与声呐之间存在相对运动时,接收信号中将观察到多普勒频移现象。设目标运动速度为v,当目标接近声呐系统时,v为正,定义脉宽压缩参数为

式中,c为声速。假设目标的初始距离为d0,则接收信号为
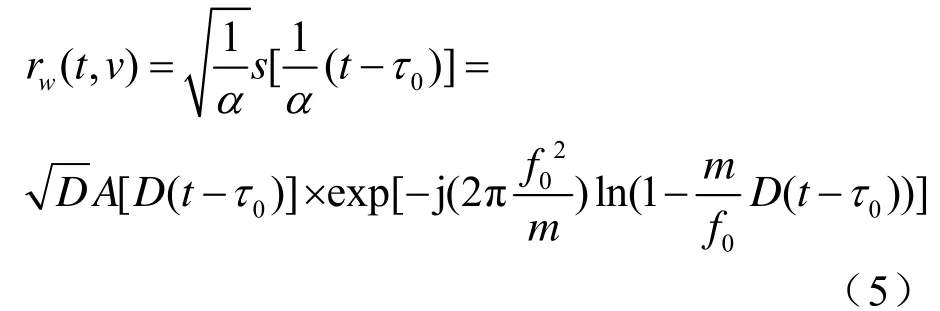
其中,D=1/α。不考虑噪声和传播损失,τ0=2d0/c,则接收信号的瞬时频率为

若一种信号的多普勒效应等效于频率调制函数在时间上的平移,接收信号的调制特性不变,则称该信号具有多普勒不变性。此时,接收信号瞬时频率的变化规律不变,只是将原信号的瞬时频率在时间上进行平移。HFM信号即多普勒不变信号。

图2 HFM信号的多普勒不变性
2.2 匹配滤波特性
匹配滤波是对发射信号和接收信号进行相关处理,使其输出信噪比达到最大。然而,当目标与声呐之间存在相对运动时,接收信号产生频移,导致发射信号和频移后信号不再匹配,探测能力降低。HFM信号由于其多普勒不变性,接收信号瞬时频率只是有一个时延,因此,用匹配滤波器接收时,可以得到良好的峰值,只是峰值的位置有一个时延,这个时延的量值为
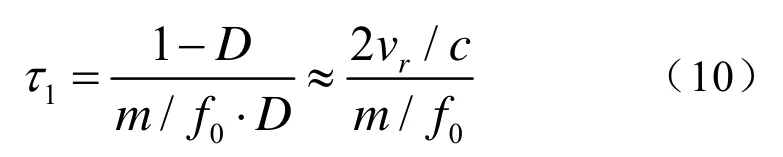
图3(a)和3(b)分别为HFM+和HFM-在目标速度为0 m/s、10 m/s、20 m/s、30 m/s时的匹配滤波输出结果。
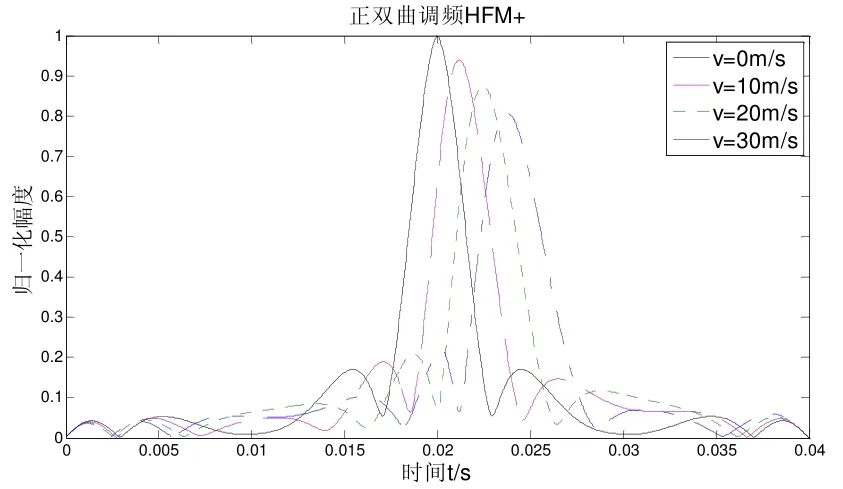
图3 (a) HFM+信号不同速度下的匹配滤波输出

图3 (b) HFM-信号不同速度下的匹配滤波输出
如图3所示,在不同速度下,匹配滤波输出的主峰突出且不存在展宽,也没有明显突出的旁瓣,且匹配滤波器的输出峰值和静止目标的峰值相比,只有轻微的衰减。随着速度的增大,匹配结果在时间轴上有所移动,速度越大,偏移越多。因此总体上来说,匹配滤波的输出峰值受多普勒效应的影响不大,仅仅产生了一个时延τ。针对正负不同的调频参数m,时延时间τ的偏移方向不同。
3 双曲调频测速测距
从双曲调频信号的模糊函数图可以看出,由于HFM信号多普勒频移分辨力很低,因此无法根据目标运动的多普勒频移进行测速。然而该信号具有很高的时延分辨力,测距精度高,工程中常用该信号来实现目标距离的估计。但单独用一个双曲调频信号进行测距时,在存在未知目标多普勒的情况下,测得信号到目标的单独往返时间会有一个与速度v有关的时延τ,从而造成测距模糊,影响其距离估计的精度。
3.1 测速测距方法
采用连续发射两个HFM信号的方法,就可以同时完成目标距离和速度的估计。先发射一个频率随时间递增的双曲调频信号HFM+(m>0),再发一个频率随时间递减的双曲线调频信号HFM-(m<0),分别测出匹配滤波出现极大值的时间t1、t2,则

式中,m为常数;f0为脉宽一半处信号的瞬时频率。联立两式,解得:

因此在测得t1、t2之后便可直接求出目标的距离和速度。
图4为连续发射的HFM+和HFM-信号匹配滤波的输出结果,其仿真条件为:发射脉冲HFM+和HFM-持续时间均为1 s;双曲调频的起始频率为fL=1.5 kHz,截止频率为fH=1.8 kHz;设定目标速度v=15 m/s。计算得到匹配滤波输出的两个极值点t1和t2,然后利用公式(13)、(14)得到目标距离R和目标速度vr。

图4 HFM+和HFM-组合信号的匹配滤波输出
3.2 性能分析
由于线性调频(LFM)信号不具备多普勒不变性,运动目标的匹配滤波结果受到多普勒频移的影响,即接收信号与发射信号不再匹配。
仿真条件:线性调频信号和双曲调频信号的中心频率均为f0=1 500 Hz,带宽B=400 Hz,脉冲宽度为T=0.5 s;设目标的运动速度为15 m/s。则LFM信号和HFM信号的匹配滤波结果如图5所示。
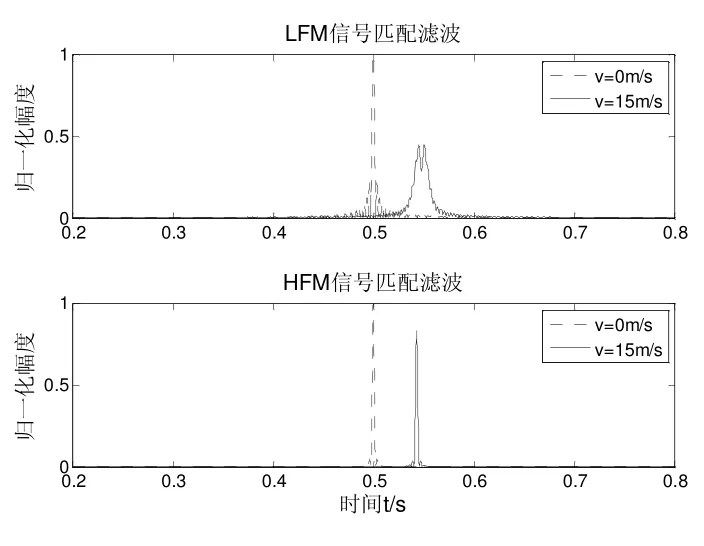
图5 LFM和HFM信号的匹配滤波输出对比
从仿真结果可以看出,当利用匹配滤波器进行目标检测时,线性调频信号的输出峰值衰减较大,且主峰展宽现象严重,从而影响着主动声呐的探测性能,也不利于目标距离和速度等参数的估计。而相比于线性调频信号,双曲调频信号由于其多普勒不变性,匹配滤波输出不存在主峰值展宽,峰值衰减也较小。因此双曲调频信号在主动声呐速度和距离的估计中,具有独特的优势。
该方法估计目标的速度和距离时,充分利用了HFM信号的多普勒不变性质,在使得匹配滤波峰值最大的基础上,考虑了由于多普勒频移而产生的时延差,也因此消除了单个HFM信号测距时由于时延τ造成的距离测量误差。
仿真条件:设HFM信号中心频率为1 500 Hz,分别计算信号脉宽为0.1 s时不同带宽条件下的距离分辨力,以及带宽为400 Hz时不同脉宽条件的距离分辨力,结果如图6所示。
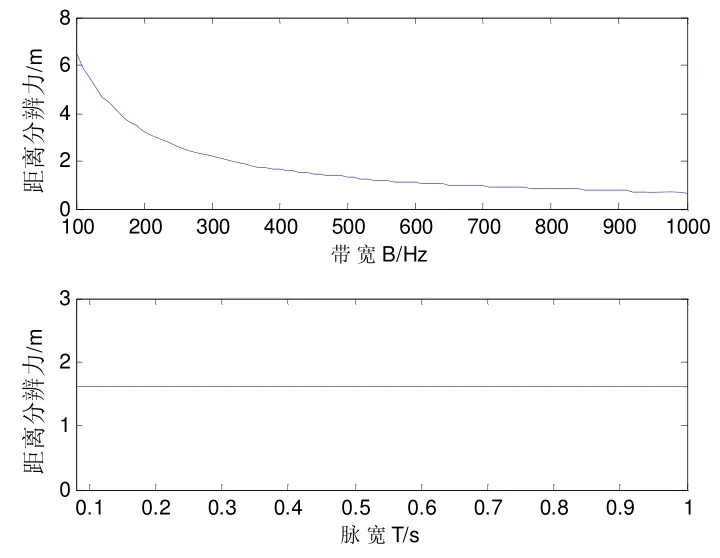
图6 HFM信号的距离分辨力
从图中可以看出,HFM信号的距离分辨力不受脉冲宽度影响;然而随着信号带宽的增加,距离分辨力提高。因此脉冲宽度一定时,HFM信号可以单独调节带宽来改变距离分辨力。
若设vr=Ac(t1−t2)=f(A,c,t1,t2),不考虑参数A与速度c的不确定度,且时间t的不确定度相同,即dt1=dt2,则速度vr的不确定度分析如下:

可以看出速度的测量精度取决于HFM信号的距离分辨力。
图7、图8分别为单频矩形脉冲(CW)信号和线性调频信号脉冲(LFM)信号的模糊函数图,可由此计算分析相应的距离和速度分辨力,结果如表1所示。
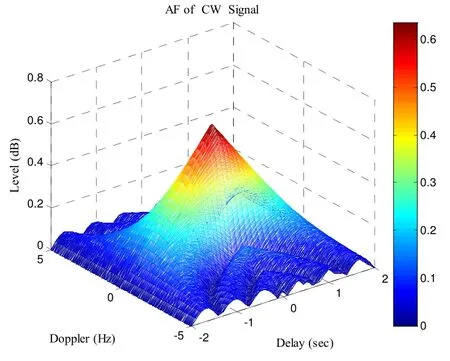
图7 CW信号模糊函数图

图8 LFM信号模糊函数图

表1 不同信号的距离和速度分辨力
4 结论
双曲调频信号(HFM)为多普勒不变信号,对于运动目标的匹配滤波结果能够使得峰值的能量损失最小。这一性质用于检测时,声呐系统的输出幅度不因目标与声呐存在相对运动而变化。因此在声呐系统中,可以利用该信号的性质进行目标速度和距离的估计。
[1]邢孟道,王彤,李真芳,等.雷达信号处理基础[M].北京: 电子工业出版社,2008.
[2]周旭广,张鹏.双曲调频信号脉冲压缩分析与仿真[J].电子科技,2014,27(1): 38-41
[3]田坦.声呐技术[M].哈尔滨: 哈尔滨工程大学出版社,2010.
[4]SONG XIUFENG,WILLETT PETER.Range bias modeling for hyperbolic-frequency-modulated waveforms in target tracking[J].IEE Journal of Oceanic Engineering,2012,37(4): 670-679.
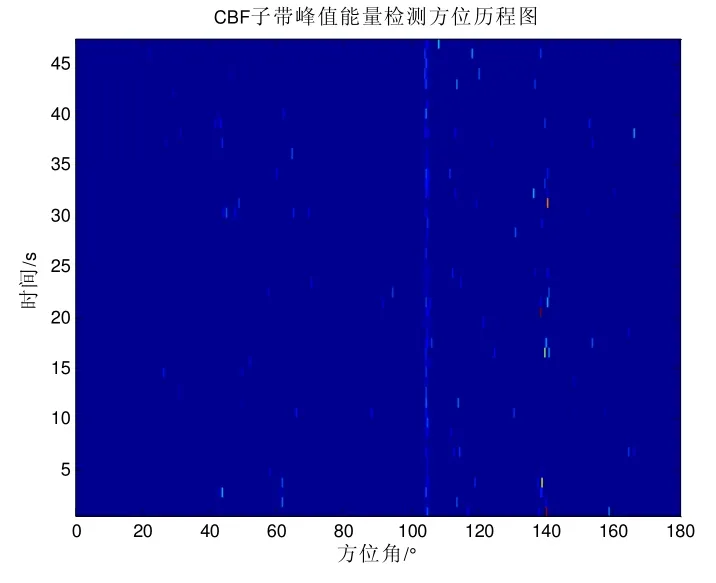
图11 子带峰值能量检测方位历程图(降虚警后)
对比图6和图7,未降虚警前,子带峰值能量检测的虚警高,目标信号淹没在虚警中;在降虚警后,子带峰值能量检测的虚警被有效降低,同时强干扰被消除。从方位历程图中可以看出,降低虚警的效果明显。
对比图6和图8,常规波束形成存在9个虚警,经过降虚警处理后虚警数目为3,虚警率降低了67%,降虚警的效果较显著。
3 结论
本文提出了时间积分、峰值筛选和剔除孤点三种降虚警方法,联合使用后能够有效降低子带峰值能量检测算法的虚警率,而且效果明显。但是,该方法只适用于宽带信号,不适用于窄带信号和低信噪比信号。降虚警处理后能够有效提高子带峰值能量检测算法的目标检测能力,对后续的目标跟踪具有非常重要的意义。
参考文献:
[1]BONO M ,SHAPO B.Subband energy detection in passive array processing[R].ADA405484,2000.
[2]杨晨辉,马远良,杨益新.峰值能量检测及其在被动声呐显示中的应用[J].应用声学,2003,22(5):31-35.
[3]李启虎.数字式声呐设计原理[M].合肥:安徽教育出版社,2003.
