一种基于波束输出方位变化特性的信号检测方法

张远洋罗明愿

（1.海军工程大学，武汉，430033；2.第七一五研究所，杭州，310023）

一种基于波束输出方位变化特性的信号检测方法

张远洋1,2罗明愿2

（1.海军工程大学，武汉，430033；2.第七一五研究所，杭州，310023）

对一种可实时实现的信号检测方法进行了分析，该方法采用分裂波束进行实时精确测向，利用实时方位序列方差对波束输出进行加权处理，仿真结果证明该方法有较好的检测效果。

信号检测；抗干扰；分裂波束；测向

由于海洋环境的多种随机不均匀性，声波经过海洋环境传输后，接收到的声信号与声源发出的声信号有着明显的区别。声呐工作者的目标是从接收到的声信号中检测、估计声源的距离、方位等信息。由于接收声信号与声源声信号的明显差异导致检测、估计目标声源信息的难度增加。如何从受到干扰的声信号中检测到声信号、并估计出其方位和距离信息是研究的难点。

在海洋环境中，通常将目标看成点源，具有确定的方位；而环境噪声和混响是散布在空间中的各个方向。更简单的描述是，当空间中存在明确的点源目标时，实时测得目标方位应该是确定的，而当空间不存在目标时，测得的方位数据应具有较强的随机性，本文利用这一区别来实现信号检测[1]。

1 信号检测原理

利用波束指向性极大值出现的位置可以确定目标的大致方位，但是方位精度是较低的。通常而言，波束都具有一定的宽度，当目标方位在一定的范围内摆动，感官上很难区分波束输出值的微小变化。所以要想较精确地确定目标方位，应该寻求一种对目标方位角的微小变化能作出灵敏反应的方法，而分裂波束形成正是这样的一种方位角精测系统[2]。如图1所示的7元圆弧阵，基元在圆周上均匀分布。

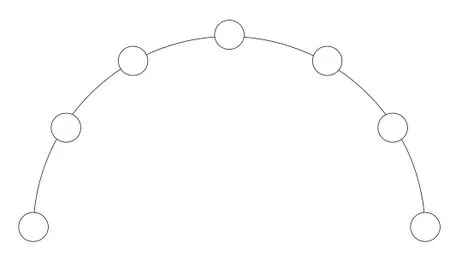
图1 圆弧阵示意图

利用分裂波束进行实时测向，图1所示阵形分成左右半阵，均为4元阵，中间基元复用。

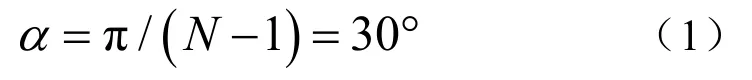
式中α为两个基元间的圆心角，N为基元数。

假定信号入射方向为θ，左半阵波束主瓣角度为0θ，左阵波束输出为

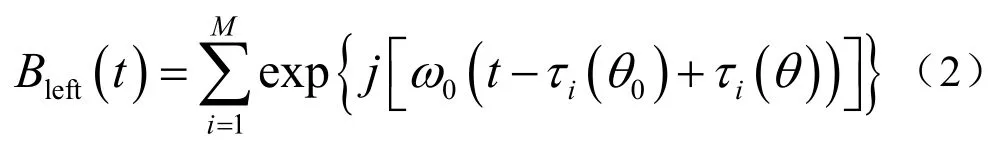
其中，s(t)=exp{j(2πft)}是入射信号的波形，ω0为其频率。τi(θ0)为波束聚焦到θ0方位时，第i号基元应补偿的时延。τi(θ)为某一基元的延迟。假设该基元的坐标位置为[x,y]，信号来向为θ，该基元相对参考位置的延迟为

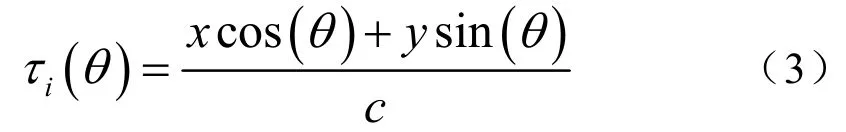
其中c为声速。对式（2）右端进行分解

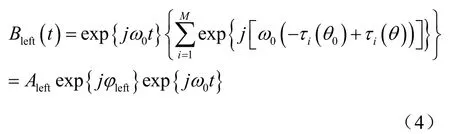
图1分解阵形的右半阵波束输出为

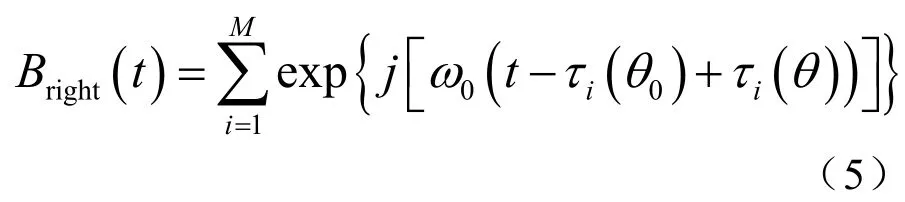
对式（5）右端进行分解有

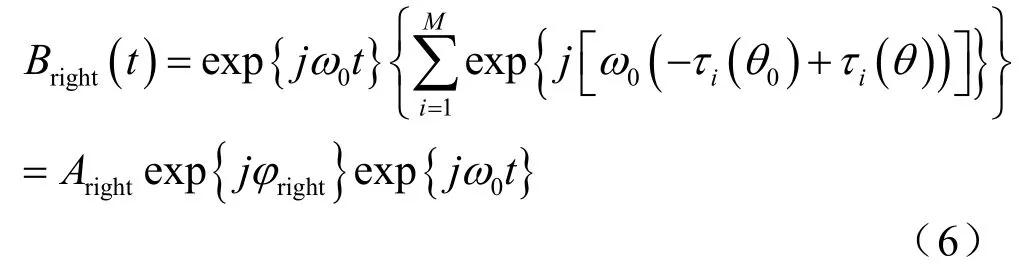
由式（4）和式（6）即可得到

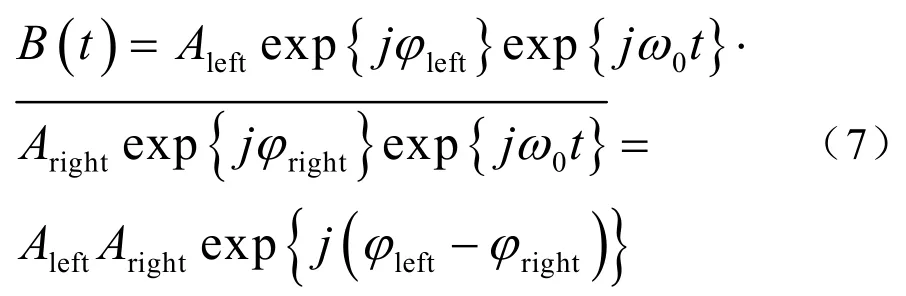
左半阵和右半阵可以分别看成一个子阵，那么左半阵和右半阵分别有一个等效声中心，此时可以将左半阵和右半阵当成一个二元阵来处理。d为基元中心间距，ω为信号角频率，λ为信号波长。由二元阵定向原理可知，当信号来向为θ时，左基元接收到的信号相对于右基元接收到的信号，相位延迟为φ，其数学表达式见式（9）。当θ很小时，可以认为sin(θ)=θ，那么式（9）可以化简为式（10）。

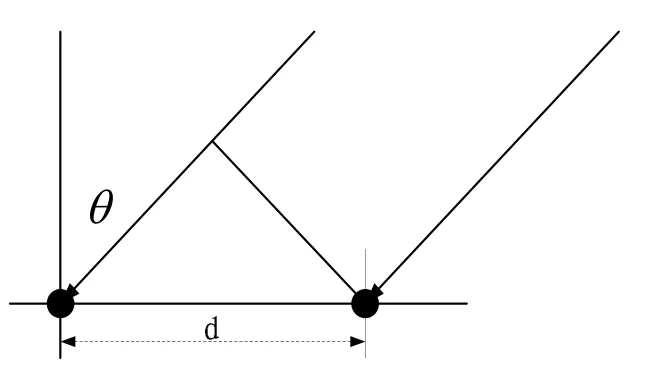
图2 二元阵定向原理

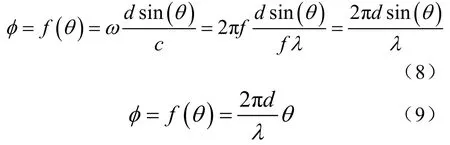
式（7）中的相位即为左半子阵和右半子阵的相位差，利用计算机仿真即可测得信号来向与左半子阵和右半子阵接收信号相位差之间的对应关系，因此可以实时测得瞬时方位。

实际中由于干扰的存在，不可能接收到纯净的信号，所以点源瞬时方位会存在干扰的影响。通常的做法是对瞬时方位序列进行统计意义上的处理，尽可能减小干扰的影响。这里对瞬时方位序列进行求解短时平均值和方差，利用瞬时方位序列的方差对波束输出进行加权处理，以达到信号检测的目的。

计算瞬时方位短时平均值和方差

利用瞬时方位方差构造权函数，对波束输出进行加权。

由式（1）～（9）的推导中可知，根据分离波束原理，对于每一对左波束和右波束的样本点，均可以得到一个瞬时的方位值，可以选取5～6个波长的样本点进行计算方位的短时平均值和方差。短时方位平均值和方位方差的实时计算公式如式（13）、（14）。

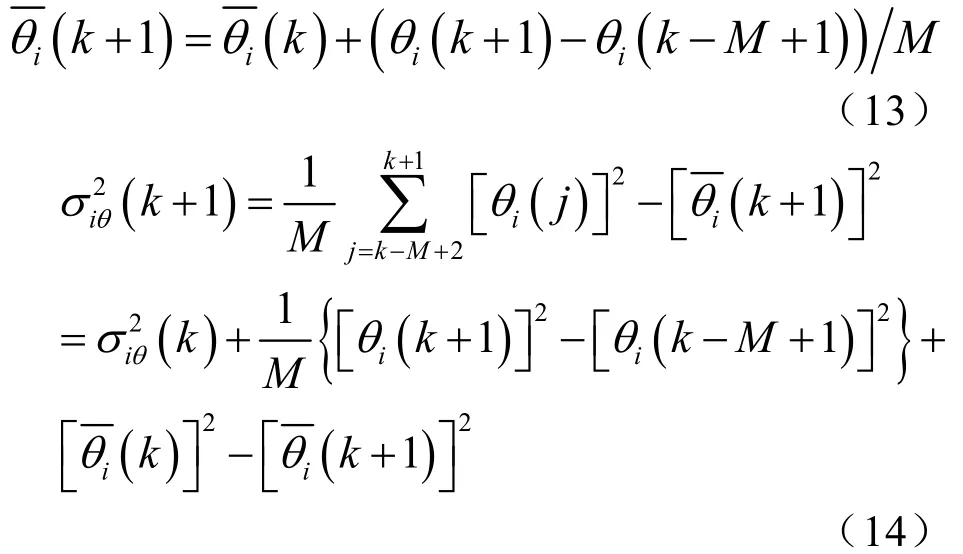
从式（13）可以看出瞬时方位短时平均值可以通过两次乘法、一次加法和一次减法实现。从式（14）可以看出瞬时方位短时方位方差可以通过一次加法、两次减法和四次乘法实现。

2 仿真分析

阵形为18元直线阵，半波长布阵，频率为4 kHz，采样频率为30 kHz，信号来向为94.5°，输出的时域信号调制到零频。图3～图10为90°波束两组信噪比条件下（−13 dB和−20 dB）的计算机仿真结果，信噪比为−20 dB的仿真结果如图3～6所示，信噪比为−13 dB的仿真结果如图7～11。

图3 常规波束输出

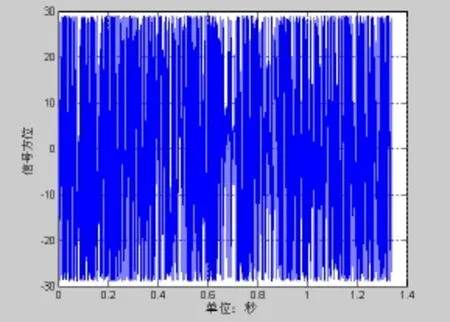
图4 瞬时方位序列

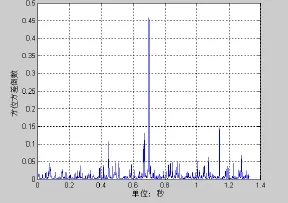
图5 瞬时方位方差倒数

图6 经瞬时方位方差倒数加权的波束输出

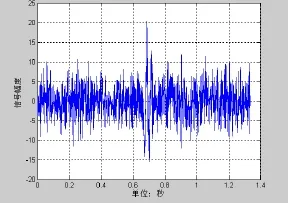
图7 常规波束输出

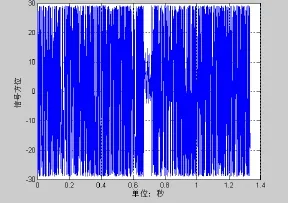
图8 瞬时方位序列

图3是信噪比为−20 dB时常规波束形成的输出信号。图7为信噪比为−13 dB时常规波束形成的输出信号。图4和图8为相应的瞬时方位序列，可以看到采用分裂波束测得的瞬时方位序列被限定在一定的范围之内，即波束形成已经对波束宽度外的干扰进行了抑制，这也是波束形成增强信号抑制干扰的体现。图5和图9为瞬时方位序列方差的倒数，有信号段的瞬时序列方差倒数明显小于无信号段。图6和图10为经瞬时方位序列方差倒数加权处理结果。将图3和图6进行比较可以发现，信号检测的概率大大增加。

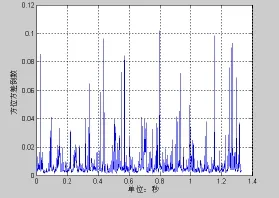
图9 瞬时方位方差倒数

图10 经瞬时方位方差倒数加权的波束输出

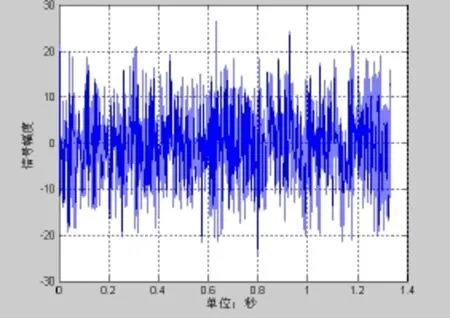
图11 60°波束输出

图12 瞬时方位序列

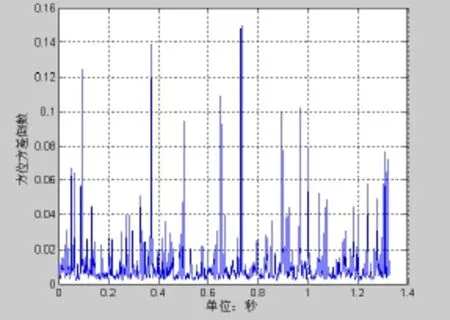
图13 瞬时方位方差倒数

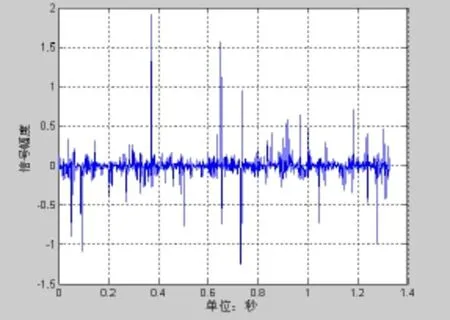
图14 经瞬时方位方差倒数加权的波束输出

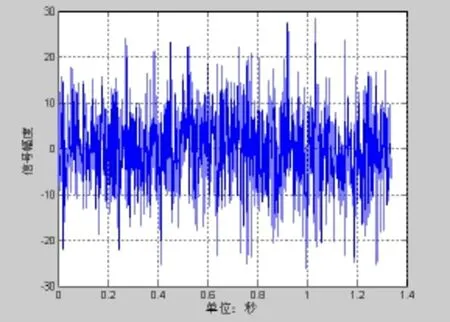
图15 120°波束输出

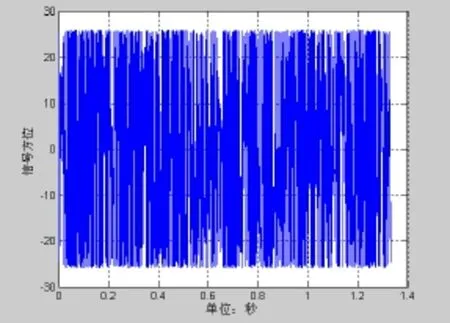
图16 瞬时方位序列

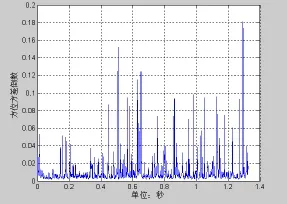
图17 瞬时方位方差倒数

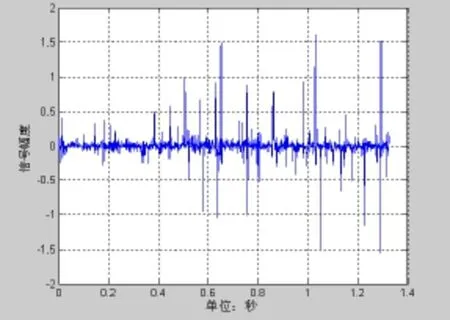
图18 经瞬时方位方差倒数加权的波束输出

图11～图14为60°的波束输出，信噪比为−20 dB，图15～18为120°的波束输出，信噪比为−20 dB。通过对比可以发现图6与图14和图18有明显的差异。

3 结论

文中对一种信号检测方法进行分析，该方法利用检测的实时方位序列的统计特征对时域数据进行加权，有效地抑制非信号段的干扰与噪声，最大限度保留信号，从而实现信号的检测，该方法适用于主动窄带信号处理。同时也应看到信号段内的噪声与干扰对方位输出序列有显著的作用，影响了真实信号输出方位的估计。后续应进一步研究信号段的噪声与干扰的抑制。

[1]梁国龙.回波信号瞬时参数序列分析及其应用研究[D].哈尔滨工程大学,1997.

[2]李启虎.声呐信号处理引论[M].北京: 海洋出版社,1985: 309.