一种基于线状目标特征点集的声呐图像配准方法

芦俊 丛卫华

(第七一五研究所，杭州，310023)

一种基于线状目标特征点集的声呐图像配准方法

芦俊 丛卫华

(第七一五研究所，杭州，310023)

针对合成孔径声呐多测线图像拼接问题，提出一种基于线状目标特征点集的图像配准思想。首先使用Canny算子找出图像中线状目标边缘，优化选取出待匹配点，构成特征点集。通过Hausdorff距离计算点集间位置结构相似程度，找到两幅图像匹配点，并消除伪配准点，最后通过配准的线状目标特征点集实现图像的拼接。实验表明，针对线状目标特征图像的点集选取和图像配准方法具有较好的配准效果。

图像配准；多测线图像拼接；Hausdorff距离；图像边缘；伪匹配点去除

图像配准指确定同一景物在两幅图像中位置的过程。它是计算机视觉和图像工程的基本研究内容之一，在自动导航、机器人视觉、目标跟踪与识别、自然资源分析等领域中发挥着十分重要的作用。随着合成孔径声呐及侧扫声呐技术发展，多测线扫海作业中大量的图像拼接成为业内急需攻克的关键技术。水声图像拼接通常分两步骤：依据导航位置进行的图像粗拼接和依据图像特征进行的精确配准拼接。计算机自动图像配准是海底地形地貌拼接还原的关键技术。

目前图像配准算法大致可分为两类：一类是基于区域灰度的图像配准算法，如使用序贯检测的图像配准方法[1]、基于傅里叶变换相位相关法的图像配准方法[2]；另一类是基于特征的图像配准算法，如使用Harris角点的匹配算法[3]、基于尺度不变特征的图像匹配方法[4]。这些方法大部分是利用图像灰度或小范围结构特征进行图像配准，这些特征在多测线水声图像中很容易改变，使配准精度大大降低。水声图像中的线状目标非常普遍，类似管道、电缆、绳索、沟槽、田埂、道路等都为线状目标，这些线状目标具有尺度大，图像结构稳定的特点，因此研究带线状目标的图像配准具有重要意义。本文提出一种基于线状目标特征点集的图像配准思想。首先使用Canny算子找出图像线状目标边缘，优化选取特征点集，通过Hausdorff比较线状目标结构相似程度，找到对应匹配点，实现平移旋转自动图像拼接。

1 基本原理

1.1 Hausdorff距离

Hausdorff距离[5-9]是特征点匹配的方法之一。它无需建立特征点之间的一一对应关系，只计算两个特征点集间的相似程度，因此可以有效处理多特征点情况。Hausdorff距离的基本概念如下：

对于两个有限点集合A={a1,a2,⋅⋅⋅,am}和B={b1,b2,⋅⋅⋅,bn}，A、B间的Hausdoff距离定义为：

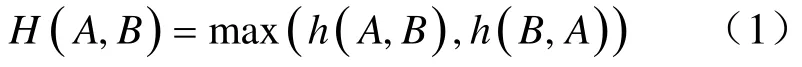
其中函数h(A,B)和h(B,A)分别称为前向和后向Hausdoff距离且有：

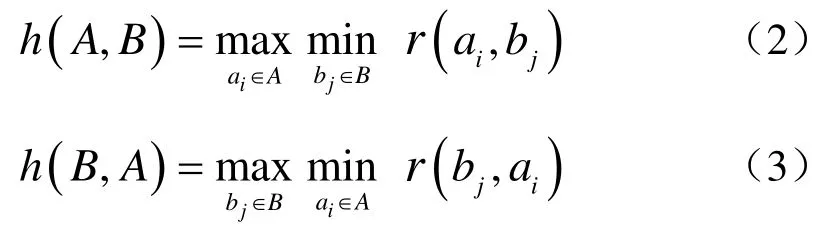
式中r(ai,bj)表示点ai、bj之间的距离范数。

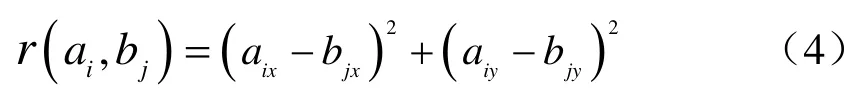
式中aix、aiy分别表示点ai的X坐标和Y坐标；bjx、bjy分别表示点bj的X坐标和Y坐标。如果h(A,B)=d，则表示A中任一点到B中某一点的距离不超过d，也就是说A中所有点都在B中点的距离d的范围之内。

Hausdorff距离可以描述两个点集之间的相似程度。但干扰对相似程度的判断影响较大。若点集A和B很相似，但B中仅有一点与A相差较大，h(B,A)的值就变得很大，从而H(A,B)很大。为了解决这一问题，Huttenlocher提出了部分Hausdorff距离概念：

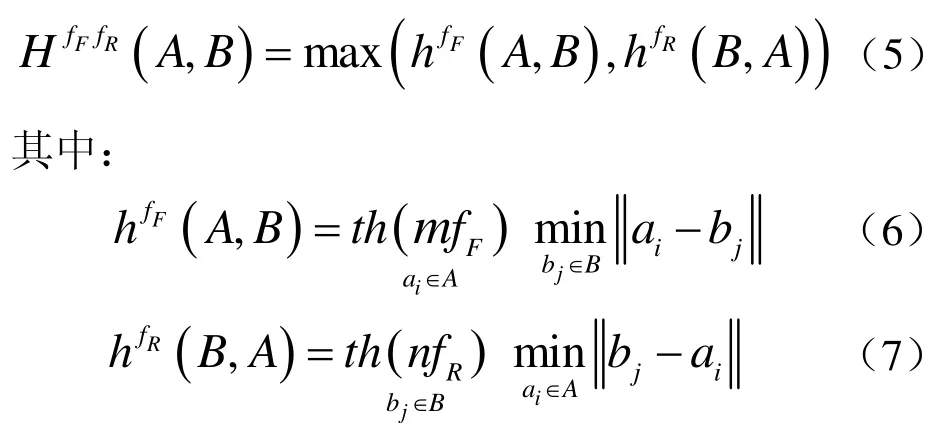
式中fF,fR∈[0,1]分别称为前向分数和后向分数，控制着前向距离和后向距离，th表示排序，以降序排列。（6）式中th(mfF)表示排序中取第个值作为的值。即可得出通过这种方法可以去除少数几个异常点对整体相似度判断的影响。当fF=fR=1时，该公式退化为原始的Hausdorff距离。

1.2 Canny算子边缘检测

Canny算子是由John F Canny开发的多级边缘检测算法。它是一种最优边缘提取算子的近似实现方法。一般包括四个步骤：高斯滤波平滑图像、梯度幅值和方向的计算、梯度幅值的非极大值抑制、双阈值检测和连接边缘。

使用2×2邻域的一阶偏导的有限差分计算平滑后图像I(x,y)的梯度的幅值和梯度方向。其中在点(i,j)处沿x方向和y方向的偏导数Px(i,j)和Py(i,j)分别为：

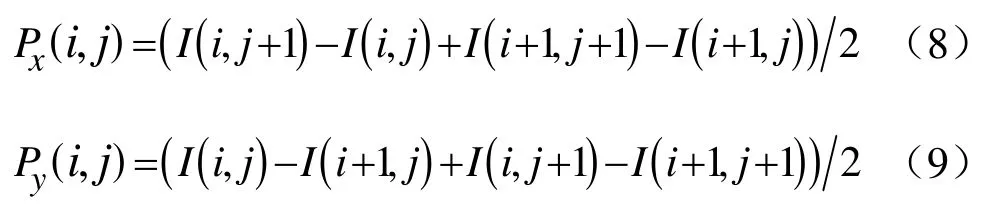
由式（8）和式（9）可计算得出梯度的幅值M(i,j)和梯度方向θ(i,j)。其中梯度幅值为：

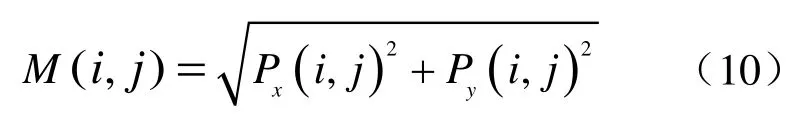
梯度方向θ(i,j)为：

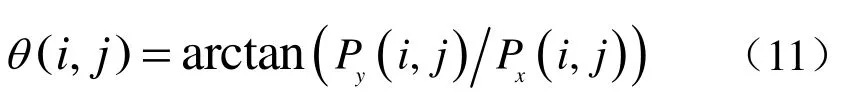
把边缘的梯度方向大致分四类（0°、45°、90°和135°）。采用非极大值抑制的方法保留局部梯度最大值，在每个像素点上，邻域的中心像素与沿着梯度方向的两个像素相比，若中心点的梯度值不比沿梯度方向的两个像素值的梯度大，则令中心像素为零。

使用双阈值分别检测出边缘，以高阈值边缘为主体，低阈值边缘连接主体断点的方法进行边缘检测。

2 算法流程

在使用本文基于线状目标特征点集的图像配准算法进行配准之前，图像需经过拖体姿态补偿后的经纬度坐标地理位置编码。编码后图像再进行去噪增强处理。

在配准阶段首先是匹配点确定，其次是点集的Hausdorff距离配准，伪匹配点去除，最后通过匹配的线状目标特征点集实现图像的拼接。本文基于特征点集的图像配准算法流程如图1所示。

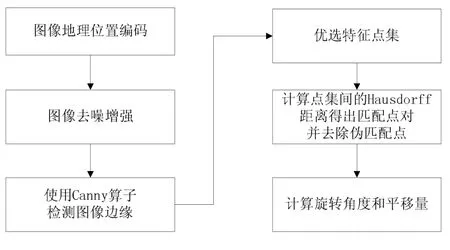
图1 基于特征点集的图像配准算法流程

2.1 图像预处理

原始水声图像大都为斜距图像，且拖体的航迹方向及其姿态不可能时刻保持理想状态。因此我们需要将图像进行地理位置编码，并通过地理位置编码找到两幅图像重叠区域。

地理位置编码首先是将斜距图像校正为平距图像；之后依据航迹经纬度坐标推算每一像素点坐标，根据推算出的经纬度坐标进行图像的重新编码；最后对重叠区域和编码缝隙分别进行融合与插值。地理位置编码后的图像需要进行图像的去噪增强后才能更好进行边缘检测。

2.2 特征点集选取

本文采用双阈值Canny算子检测重叠区域图像中的线状目标边缘。如果等边缘长度选取N个匹配点，线状特征样本较多。既不能有效反映图像特征，又不利于运算。为此我们边缘曲率低的部分选取较少特征点，曲率高的部分选取更多特征点。这样能在保证质量的前提下较快完成配准。

首先等边缘长度选取N个匹配点，计算边缘和所有相邻两匹配点间所围区域面积，取最大值，设为面积阈值ε。然后从端点A开始沿曲线选取匹配点B，使A、B所成线段和曲线所围面积等于ε时，即可确定B点。然后从B点开始使用同样方法依次选取其他匹配点，如图2、3所示。图3中待匹配点比图2中少。

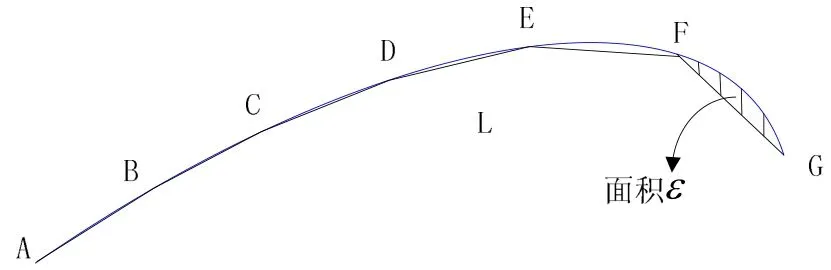
图2 面积阈值求解示意图

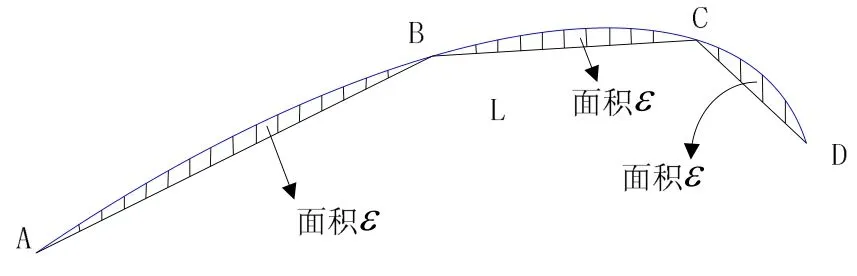
图3 匹配点选取示意图

我们以每个匹配点为原点，计算其他匹配点坐标形成一系列点集。图4所示分别是以待匹配点B、C点为参考点，由其他点坐标构成特征点集{A,B,C,D}和{A′,B′,C′,D′ }。

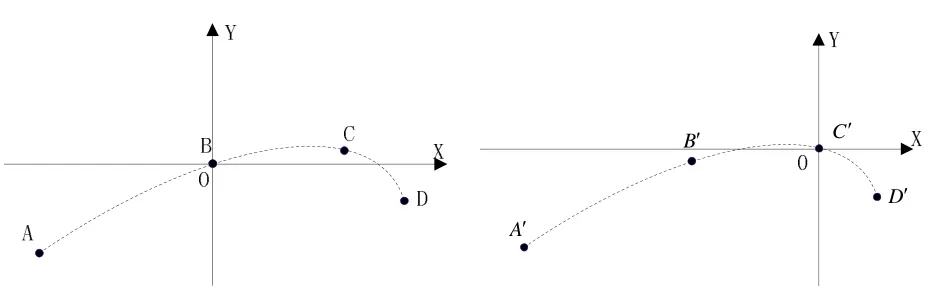
图4 点集计算示意图

2.3 Hausdorff距离相似度检测

若待匹配两幅图像分别有M和N个待匹配点，则可分别得出M和N个点集，对M中每个点集，计算其与N中每个点集的Hausdorff距离，Hausdorff距离最小的两个点集的参考点即为所求配准点。总共可求出M对配准点。匹配准则为：所选的匹配点对需小于2倍的最小Hausdorff距离。

2.4 伪匹配点去除

由于图像间正确匹配点能较好的保持相对位置且距离上相等，如图5所示。伪匹配点往往具有随机性，如左图中的点D到A、B、C的距离并不等于右图中的点D′到A′、B′、C′的距离。

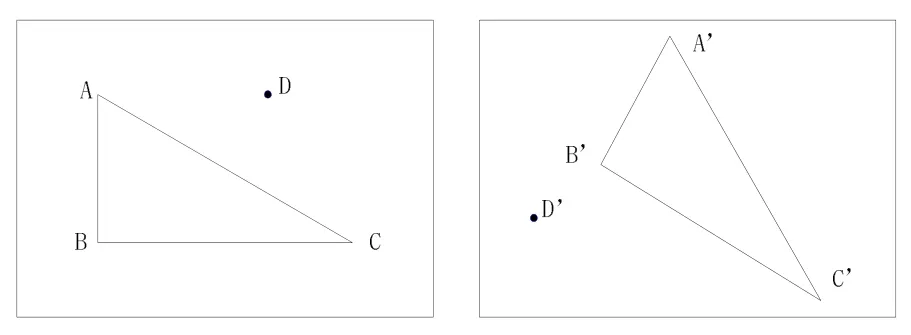
图5 匹配点示意图

定义距离差异函数：

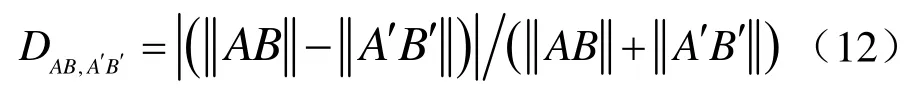
可知距离差异函数越小，点对间的正确配准可能性也就越大。由于距离差异函数为[0,1]，若DAB,A′B′<0.1，定义可信度函数CrAA′、使CrBB′均加上1。由此可累计得出每个配准点的可信度。通过可信度阈值判断，排除伪匹配点。

2.5 旋转角度和平移校正

得到匹配点对，可根据匹配点对间位置结构关系计算旋转角度和平移量，如图6所示。在同一坐标系中计算向量和向量，旋转角度iθ为：

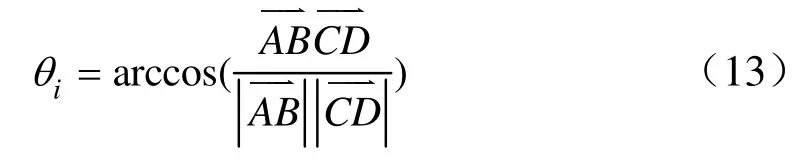
为提高统计精度，我们取多对匹配点进行统计平均：

对于平移量，我们分别计算旋转校正后两幅待匹配图中所有匹配点的坐标均值，计算两坐标均值所组成向量即为平移向量。

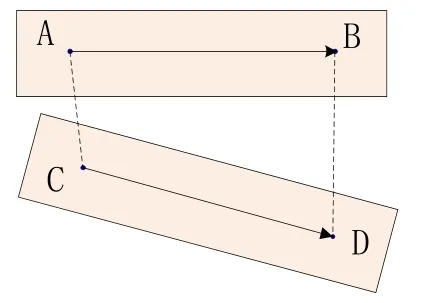
图6 计算角度旋转和平移示意图

3 实验数据分析

为验证本文算法，采用带线状目标的合成孔径声呐水声图像进行配准实验(图7~图11是数据处理过程中产生的分析结果，因此略去横纵坐标)。图像已经完成地理位置编码和去噪增强处理，两幅待配准图如图7所示。

图7 （a）待配准图

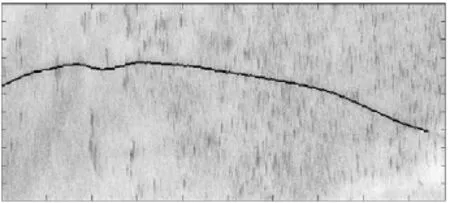
图7 （b）待配准图

采用Canny算子进行图像边缘提取。对于图像中的线状目标，Canny算子能找到上下两条边缘，提取出的边缘中心二值图像如8所示。

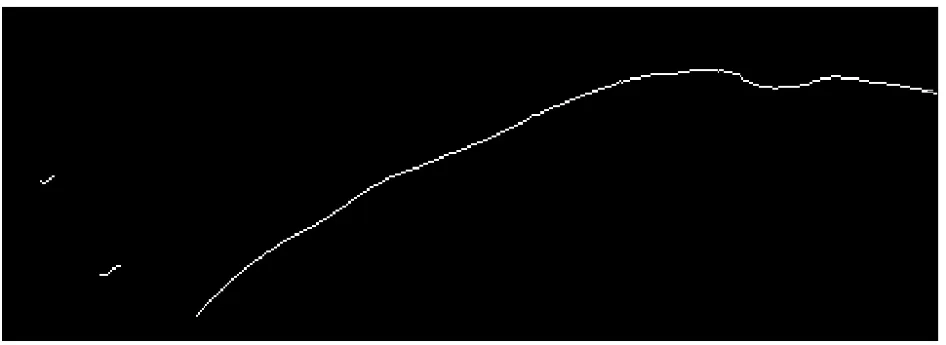
图8 （a）提取出的边缘

图8 （b）提取出的边缘

对提取出的a、b两条长边缘，分别等分成100段和200段，得出面积阈值后，使用面积阈值进行匹配点选取，得出的匹配点如图9所示。

图9 （a）匹配点选取

图9 （b）匹配点选取

筛选出的匹配点如图中“*”号所示，使曲率高的部分匹配点密集，曲率低的部分匹配点稀疏。从而使总匹配点数大大降低。

计算图9中点集间的Hausdorff距离，取最小Hausdorff距离的2倍之内的对应点集得到候选匹配点对。如图10所示。

图10 匹配点的配准结果

图10经过Hausdorff距离筛选，出现较多伪匹配情况。计算距离差异函数，使用累计可信度函数方法去除25个伪匹配点后所得配准结果图如图11。

图11 去除伪匹配点后匹配结果

得到配准点对后即可进行图像拼接等各种后续处理。实验数据图像拼接后得出宽幅图像，如图12所示。

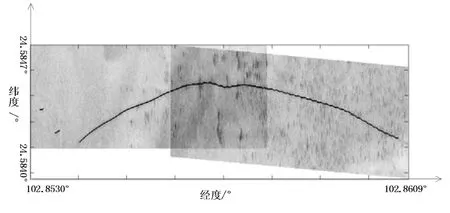
图12 图像拼接结果

4 结论

本文提出基于声呐图像线状目标特征点集的图像配准思想：首先提取图像中线状目标的边缘，然后优化选取待匹配点构成特征点集，最后利用Hausdorff距离找到配准点后实现图像拼接。实验表明，本文方法很好利用线状目标位置结构信息进行图像的配准，具有一定的工程应用价值。

[1]PARNEA D I,SILVERMAN H F.A class of algorithm for fast digital image registration[J].IEEE Transactions on Computing,1972,21:179-186.

[2]THEVENAZ P,UNSER M.An efficient mutual information optimizer for multiresolution image registration[C].Proceedings of the IEEE International Conference on Image Processing,1998P:833-837.

[3]HARRIS C,STEPHENS M.A combine corner and edge detector[C].Alvey Vision Conference,1988:147-151.

[4]BAY H,TUVTELLARS T,GOOL L VAN.SURF:speed up robust features[C].Conference on Computer Vision,2006.

[5]HUTTENLOCHER D P,KLANDERMAN G A,RUCKLIDGE W J.Comparing images using the Hausdorff distance[J].IEEE Trans.On Pattern Analysis and Machine Intelligence,1993,15(9):850-863.

[6]牛力丕，毛士艺.基于Hausdorff距离的图像配准研究[J].电子与信息学报,2007,29(1): 35-38.

[7]RUCKLIDGE W J.Efficiently locating objects using the Hausdorff distance[J].International Journal of Computer Vision,1997,24(3):251-270.

[8]SON H J,KIM S H,KIM J S.Text image matching without language model using a Hausdorff distance[J].Information Processing and Management,2008,44(3): 1189-1200.

[9]鲁珊，雷英杰．基于空间点特征和改进Hausdorff距离的图像配准方法[J].系统工程与电子技术,2011,33(7): 1664-1667.