随机规划在泵站树状给水管网优化中的应用

寇海群

（新建县环境保护监测站，南昌 330100）

随机规划在泵站树状给水管网优化中的应用

寇海群

（新建县环境保护监测站，南昌 330100）

泵站树状给水管网流量具有随机性，而这种随机性变化会直接影响管网的建设费用和动力费用。针对这一特点，应用随机规划原理，建立泵站树状给水管网机会约束模型，编写基于随机模拟的遗传算法程序求解该模型。机会约束模型能较客观地反映该管网的实际工况，使优化设计结果更符合实际。

泵站；树状给水管网；随机规划；机会约束模型；遗传算法

泵站树状给水管网一般投资较小，广泛用于村镇供水，在环境保护部公布的《国家级生态乡镇建设指标》中，要求城镇建成区自来水、排水管网等公共设施完善，集中式饮用水水源地水质达标率100%。泵站树状给水管网优化设计的目的就是在保证各节点所需的压力和流量条件下，为生态乡镇类型的建设项目寻求系统最经济的设计方案。

传统的泵站树状管网优化设计模型中［1-5］，均将流量作为确定值进行优化设计，属于确定性优化设计模型。这种方法的优点是优化设计的模型简单，便于求解，但没有考虑实际用户的用水量具有随机性，而流量的随机变化直接影响到泵站树状给水管网的建设费用和动力费用。本文考虑到流量的随机变化对投资及供水可靠性的影响，在确定性优化模型的基础上，应用随机规划理论，建立符合泵站树状给水管网实际要求的随机规划模型，并编写了改进的遗传算法程序求解该模型。

1 泵站树状给水管网机会约束优化模型的建立

1.1 机会约束规划

由Charnes和Cooper提出的机会约束规划主要是针对含有随机变量，且必须在观测到随机变量的实现之前做出决策的情况[6，7]。考虑所作的决策在事故情况发生时可能不满足约束条件，而采取的一种原则：即允许所做决策在一定程度上不满足约束条件，但该决策使约束条件成立的概率或可能性不小于某一置信水平。

典型的机会约束规划优化问题可以表示成下面形式：

1.2 泵站树状给水管网用水量变化的规律

由于供水系统用水对象个数的不确定性以及每个对象用水量的不确定性，将引起系统用水量的随机性变化，因此给水系统的流量具有随机性。而不同地区给水系统水量的变化规律及服从的概率分布是各不相同的，应通过对给水系统所在地区的气候、人口、工业发展情况进行实际调查来确定。

据上述分析，区域用水量具有随机性，一般为正态分布[8]，反映在树状管网设计中，即管道的设计流量符合正态分布，其中为最高日平均时期望值流量，为最高日时用水量变化标准方差。同时为了提高供水的可靠性,各种约束条件均要满足一定的置信水平。

1.3 泵站树状给水管网机会约束优化模型的建立

根据以上分析，在泵站树状给水管网随机优化设计中，根据管道流量随机变化的特点，把管段流量作为随机变量进行机会约束优化具有重要的现实意义。为了说明设计中不确定性对管网优化设计年费用的影响，采用遗传算法分别计算不同方差情况下的流量变化时的管网系统的年费用值，其中当方差时表示计算确定性的管网情况，越大表明不确定性越大。同时计算不同置信水平即约束条件满足的不同程度下的年费用值，置信水平越高表示满足模型中约束条件的可能性越高，相反，满足约束条件的可能性越低。

1.3.1 目标函数

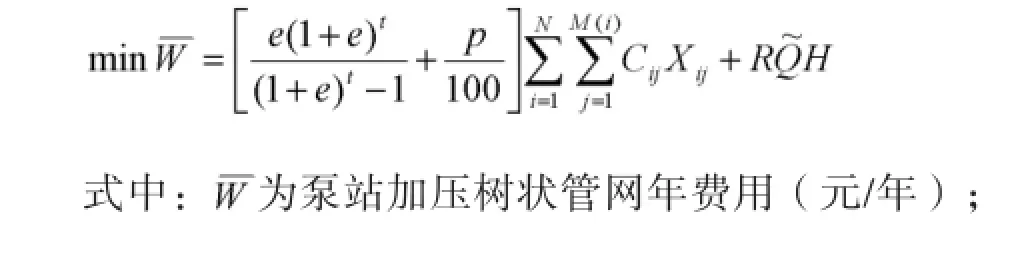
2 模型的求解及应用

2.1 模型的求解

为了求解泵站树状管网优化的模型，本文编制基于随机模拟的遗传算法程序求解该模型，遗传算法[9-12]采用浮点向量表示单个染色体，并定义染色体个数为整数N。在决策向量X的可行域中产生一个随机点，运用随机模拟方法检验其可行性，编写程序的步骤如下：

（1）准备好初始数据，包括管网各管段的流量和管长以及标准管径系列各种规格管径单位长度造价等，将这些数据直接输入计算程序中。

（2）利用随机数发生器构造出由I个个体组成的初始群体，每个个体有J根管段，用一个I×J维的数组P[I] [J]来存放I×J根管段。

（3）对初始群体进行随机模拟的管网水力计算和年费用值计算，根据适应函数计算各个体的适应度值，然后再根据个体适应度值的大小对个体进行选优，把最优个体存放到数组P[M][N]的第一行中；然后再对群体进行选择操作、交叉操作、变异操作，从而产生新一代群体，再对新群体进行水力计算，判断各个体是否满足水压和流速条件。

（4）当进化代数未达到最大进化代数GENMAX时，重复进行上述步骤，直到满足算法终止规则；当进化达到最大进化代数GENMAX时，算法结束，输出最优解。

2.2 算例

2.2.1 基本资料

泵站树状给水管网布置如图1所示。采用钢筋混凝土管，管道单价见表1，管道粗造系数n = 0.013，管道承压力为0.4MPa。要求节点服务水压为12m，管网各节点地面高程见表2，P= 5%，t = 20年，h= 0.2，b = 0.3，e = 8%，= 0.2元/kW·h，= 0.7；当水源水面高程 E0=30.2m时，确定管网优化设计方案。

图1 泵站加压树状管网计算图

表1 管道单价

2.2.2 确定各管段备选管径

根据图1可知，各个节点的节点流量，从而求出各个管段的管段流量，给水管道流速要求确定各管段的备选管径（见表2）。

表2 备选管径组

2.2.3 算例参数的确定

流量随机变化的方差σ取：σ1= 0.001 ；σ2 = 0.002；σ3 = 0.003；σ4 = 0.004；σ5 = 0.005。

本算例设定遗传算法运行参数为：种群规模为N = 100；交叉概率为 Pc= 0.2。

变异概率Pm= 0.05；终止代数T= 500；随机约束检验次数为：n= 200。

2.2.4 结果计算及分析

将以上基础数据带入编写的基于随机模拟的遗传算法程序，求出该算例的结果见表3、表4，在泵站树状给水管网机会约束优化模型中由于约束的置信水平和正态分布参数取值不同计算的费用和优化的结果也不同（当置信水平α=β=1.00、方差σ= 0时，表示泵站树状给水管网流量不变的情况，即为确定性规划）。

根据表4结果绘制出的流量随机变化对应费用的变化趋势见图2。

由图2可分析出：1）当约束满足的置信水平增大时其相应的费用也就越高，系统满足实际要求的可靠度也就越高；2）当反映流量随机变动的正态函数的方差增大时系统的费用也增大。

图2 流量随机变化与年费用变化的关系

可见，在进行泵站树状给水管网优化设计时为了最大限度地满足实际需要，提高供水的可靠性，就要提高约束满足的置信水平，相应的费用也会增加。同时因为流量的随机变化规律对提高系统设计的可靠性以及费用起关键作用，需要在设计初期能准确预测出该地区的流量分布函数，这是影响该模型计算结果的重要因素。

表3 备选管径优化计算结果 （单位：m）

表4 费用和扬程结果

3 结语

泵站树状给水管网优化设计机会约束模型是在确定性泵站树状给水管网优化设计的基础上考虑了流量随机性变化，应用随机规划的理论而进行的优化设计。该方法由于考虑了流量的随机性变化，与系统的实际工况更接近，从而能充分发挥该系统的功能。

[1] 白丹.树状给水管网的优化[J].水利学报，1996，（11）：52-56．

[2] 李永顺.树状管网管径优化的线性规划法[J].农田水利与小水电，1991，（1）：31-34．

[3] 付玉娟.基于列队竞争算法的变权值树状管网优化布置[J].水利学报，2008，39（12）：1321-1326.

[4] 周荣敏.应用单亲遗传算法进行树状管网优化布置[J].水利学报，2001，（6）：14-18.

[5] Davidson J，W，GoulterI C.Evolution Program for Design of Rectilinear Branched Networks[J].Comp in Civ Engrg，1995，9（2）：112-121.

[6] Charnes A，Cooper WW.Chance-constrained programming.Managenen-Science.1959，6（1）: 73-79.

[7] 刘宝碇，赵瑞清，等.不确定规划及应用[M].北京：清华大学出版社，2003．

[8] 严煦世，赵洪宾.给水管网理论和计算[M].北京：中国建筑工业出版社，1986．

[9] 苑希民，等.神经网络和遗传算法在水科学领域的应用[M].北京：中国水利水电出版社，2002．

[10] 周明，孙树栋.遗传算法原理及应用[M].北京：国防工业出版社，1999．

[11] 马孝义，范兴业.基于整数编码遗传算法的树状灌溉管网优化设计方法[J].水利学报，2008，39（3）：373-378.

[12] 王新坤.基于模拟退火遗传算法的自压树状管网优化[J].水利学报，2008，39（8）：1012-1016．

[13] 严煦世，范瑾初.给水工程(第三版)[M].北京：中国建筑工业出版社，1995.

Application of Randomizing Planning in Optimization of Network of Dendritic Service Pipes of Pumping Station

KOU Hai-qun
(Xinjian County Environmental Protection Monitoring Station, Nanchang 330100, China)

The flow of network of dendritic service pipes of pumping station has random, but the random change can directly affect the construction costs and power costs of pipe net work. Based on this characteristic, the paper applies the principle of randomizing planning, sets up chance-constrained programming of network of dendritic service pipes of pumping station, compile the inheriting arithmetic procedure and solve the model. The opportunity and restricted model can objectively reflect the actual work condition, so that the optimization design result can accord with the practice.

pumping station; network of dendritic service pipes; random planning; opportunity and restricted model; inheriting arithmetic

TU991.3

A

1006-5377（2014）11-0030-05