基于Curvelet变换和SPIHT算法的医学图像感兴趣区压缩

2014-03-10陈秀梅CHENXiumei

中国医学影像学杂志 2014年10期

关键词：于小波小波队列

陈秀梅 CHEN Xiumei

王伟 WANG Wei

汤敏 TANG Min

基于Curvelet变换和SPIHT算法的医学图像感兴趣区压缩

陈秀梅 CHEN Xiumei

王伟 WANG Wei

汤敏 TANG Min

目的提出基于Curvelet变换和多级树集合分裂排序（SPIHT）算法的图像感兴趣区（ROI）压缩方法，并应用于医学图像压缩。资料与方法算法流程首先对图像ROI进行提取，保留ROI不压缩，对背景区域进行Curvelet变换，采用SPIHT算法对Curvelet系数进行编码；然后进行Curvelet逆变换得到有损压缩后的图像；最后将ROI区域与背景区域叠加，得到压缩后的完整图像。采用峰值信噪比作为评价指标，比较ROI压缩和整体压缩的效果，以及小波变换和Curvelet变换用于图像压缩的效果差异。结果分别对测试图像和医学图像的压缩结果进行比较，采用ROI压缩的视觉效果优于整体压缩的效果，更能突出ROI；而采用Curvelet变换压缩的峰值信噪比高于小波变换压缩，相同比例的压缩图像也更清晰。结论基于Curvelet变换和SPIHT算法的ROI压缩可在保证不丢失重要诊断信息的前提下实现图像的高效压缩，符合医学图像压缩的高精度、高质量要求。

数据压缩；图像感兴趣区域压缩方法；图像编码；算法；图像处理，计算机辅助；Curvelet变换；SPIHT算法

近年来，医学影像设备产生了大量的医学图像。由于医学图像要求高质量、高分辨率、多量化级，因而一般数据量较大，给图像存储和传输均带来了巨大挑战。因此医学图像压缩研究成为一个重要而且亟需解决的问题。医学图像压缩具有不允许丢失细节诊断信息的特殊性，因此长久以来均采用无损压缩方式。尽管该方式可以从压缩数据中精确地恢复原始图像，但是压缩效率太低，已经无法满足日益庞大的医学图像数据压缩需求。因此人们一直尝试使用有损压缩的方式对医学图像进行压缩，即只要诊断信息不丢失，有损压缩方法是可行的[1]。

由于小波变换只能反映奇异点的位置和特性，为了克服小波变换在处理高维信号时的不足，Candes等[2]提出了具有多尺度多方向特性的Curvelet变换，能够有效地描述具有曲线或超平面奇异性的高维信号，可以保留更多的图像边缘信息，更适用于医学图像处理。近年来，Curvelet变换在图像压缩方面的研究取得了一定的进展[2-4]。Do等[5]和Maske等[6]使用快速算法实现的可逆非冗余的正交有限脊波变换将Curvelet变换应用于图像压缩。一些学者联合Curvelet变换和迭代树结构的滤波器组、离散余弦变换、迭代硬阈值算法以及支持向量机算法应用于图像压缩，提高了运算时间和重建质量[7-12]。Reddy等[13]采用多级树集合分裂排序（set partitioning in hierarchical trees, SPIHT）算法对图像进行压缩，但在压缩率较高时图像出现伪影，仍需进一步改善。

本文基于Curvelet变换理论和SPIHT算法对医学图像感兴趣区（ROI）压缩进行研究。首先提取图像的ROI，并完整保留ROI的图像细节，不对其进行任何压缩处理；对于背景区域（back ground, BG）则采用Curvelet变换，利用SPIHT算法对Curvelet系数进行编码，然后对处理后的Curvelet系数进行逆变换重建出图像；最后将ROI和压缩后的BG叠加，得到压缩后的完整图像。在进行医学图像压缩时，保留图像ROI的细节，而对BG采取有损压缩，在不丢失重要诊断信息的同时能最大可能地减少数据量，这在医学领域具有重要意义和应用前景。

1 算法流程和基本原理

1.1 算法流程首先选取图像ROI并提取，其余部分则为BG，对ROI保留图像细节不进行任何处理，而BG采用Curvelet变换提取区域特征信息，同时利用SPIHT算法对Curvelet系数进行编码和传输，在解码端则实现BG的接收和解码，从而使图像的压缩质量得到提高（图1）。

图1 算法流程图。上半部分为图像压缩过程，下半部分为解压过程

1.2 Curvelet变换 Curvelet变换是一种多尺度几何分析方法。与小波变换相比，Curvelet变换除了尺度和位移两个参量外，还增加了一个方向参量[14]，具有更好的方向识别能力，克服了小波变换只能反映奇异点的位置和特性以及在表示图像的边界和线状特征时存在的不足[15]，常用作对不连续边缘的优化稀疏表示。因此对图像边缘几何特征的表达优于小波变换，具有更好的应用前景。

Curvelet变换和小波变换、脊波变换理论都属于稀疏理论的范畴，均采用基函数与信号的内积形式来实现信号（或函数）的稀疏表示。则Curvelet变换可表示为，其中，Φj,l,k表示Curvelet函数，j,l,k分别表示尺度、方向和位置参量[16-18]。

若以笛卡尔坐标系下的f[t1,t2](0≤t1,t2＜n)为输入，Curvelet变换的离散形式[16]为公式（1）：

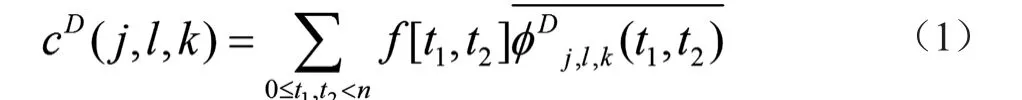
用公式（2）实现多尺度分割，对于每一个ω=(ω1,ω2),ω1＞0，则有：

目前第二代Curvelet变换可以通过非等间距快速傅里叶变换（unequally-spaced fast fourier transform, USFFT）和Wrapping两种方法实现[19,20]，本文采用Wrapping算法。

Wrapping算法实现过程如下：①对于给定的一个笛卡尔坐标下的二维函数f[t1,t2](0≤t1,t2＜ω)进行二维快速傅里叶变换，得到二维频域表示fj,l[n1,n2]，－n/2≤n1,n2≤n/2。②在频域对每个尺度、方向参数(j,l)获得乘积Uj,l[n1,n2] f[n1,n2] 。③在原点附近缠绕上述乘积得到fj,l[n1,n2]＝W(Uj,l,f)[n1,n2]，对f进行局部化处理，其中0≤n1＜L1，0≤n2＜L2。④对fj,l进行二维快速傅里叶逆变换，得到Curvelet系数CD(j,l,k)。

1.3 SPIHT算法 SPIHT算法是在EZW编码算法的基础上提出的[21]。该算法既继承了EZW算法的优点，又采用了空间方向树、全体子孙集合D(i,j)和非直系子孙集合L(i,j)的概念，以便更有效地表示上述特征的系数结构，从而提高了编码效率，同时支持渐进式传输及无损压缩。

由于基于小波变换的SPIHT算法不能有效表达图像纹理和轮廓细节[21-23]，因此本文采用基于Curvelet变换的SPIHT算法进行图像压缩编码，计算步骤如下：符号定义及初始化：定义正整数n=foor(log2(max﹛│C│﹜))，其中C为Curvelet系数，阈值 T=2n。若Curvelet系数大于等于该阈值则标识为重要系数，否则为非重要系数。

采用坐标(r,c)标识节点，定义O(r,c)为节点(r,c) 所有孩子的集合；D(r,c)为节点(r,c)所有子孙的集合（包括孩子）；L(r,c) 为节点(r,c)所有非直系子孙的集合（不包括孩子）；H为所有树根的坐标集（所有Curvelet系数对应的坐标构成的集合）。

定义LSP（重要系数表）为空集；LIP（不重要系数表）= ｛(r,c)│(r,c)∈H｝； LIS（不重要子集表）= ｛D(r,c)│(r,c)∈H且(r,c)具有非零子孙｝。LIS的初始值为“D”型表项，LIS和LIP中Curvelet变换系数的排列顺序按从上至下、从左到右的Z型次序排列。

排序扫描：扫描LIP队列，判断其中的每个Curvelet变换系数的（r,c）是否重要，是重要系数则将其从LIP队列删除，并添加到LSP队列。扫描LIS队列，判断其中的每个子集的树根(r,c)的类型，是“D”型表项，则将判断出的重要系数添加到LSP队列，不重要系数添加到LIP队列。判断L(r,c)是否为空集，如果非空集，则将（r,c）作为“L”型表项添加到LIS；如为空集，则将“D”型表项从LIS队列中删除。如果（r,c）是“L”型表项，则将重要系数的4个孩子一次添加到LIS队列中，并将“L”型表项（r,c）从LIS对列中删除。

精细扫描：将上次扫描的LSP队列记为LSP-old，对于(r,c)∈LSP-old，将Curvelet变换系数C转化为二进制表示Βr，输出Βr中第n个最重要的位到精细位流Rn。

更新阈值指数：将阈值缩小一半，返回STEP2开始执行下一代编码扫描。

2 实验分析

实验在普通配置计算机（CPU主频2.8 GHz，内存512 M）上采用matlab8.0编程实现，实验对象如图2所示，以峰值信噪比（peak signal to noise ratio, PSNR）为定量指标、人眼观察为定性指标，对图像压缩质量进行评价[24]。

首先对图2A所示Lena测试图像（512×512）进行实验，结果见图3、4和表1、2。

由图3可以看出，ROI为Lena图像的人脸区域，以白色标注作为分界线。对Lena图像进行整体压缩，当保留较少Curvelet系数时，图像非常模糊，无法在减少数据量的同时突显重点区域；随着保留系数的增多，图像逐渐清晰，但仍然无法区分出ROI。对Lena图像进行ROI压缩，当BG保留较少Curvelet系数时，模糊了背景，突出了人脸特征，在大大减少数据量的同时突显出ROI；随着BG保留的Curvelet系数增加，图像逐渐清晰，人脸始终保持不变。由表1可知，PSNR随着保留系数比例的增加而增大，且ROI压缩视觉效果更明显。

进一步比较基于Curvelet变换和小波变换的ROI压缩效果。在Curvelet分解尺度指数和边缘指数的条件下，基于Wrapping算法的Curvelet系数为739 001个。而由于Haar小波用于图像处理具有速度快、处理方便、图像压缩比高、图像特征保持性好等优点[25]，在采用Haar小波进行3层小波分解时小波系数只有262 144个，可见Curvelet系数与小波系数相差近3倍，因此不能保留相同比例的系数来比较小波变换和Curvelet变换的效果，只能在保留相同系数个数的情况下比较两种变换应用于图像压缩的性能指标。从图4可以看出，在保留较少Curvelet系数时，图像BG较模糊；在保留较少小波系数时，图像BG出现马赛克现象；随着保留系数的增加，基于上述两种算法的压缩图像均逐渐清晰。从表2可以看出，在保留系数较少时，小波变换用于图像压缩的PSNR较大；但随着保留系数的增多，Curvelet变换的压缩效果优于小波变换，且Curvelet变换可保留的系数远大于小波变换，基于小波变换的图像ROI压缩后的PSNR最大为48.9635 dB，而基于Curvelet变换的图像ROI压缩后的图像能无限逼近原图像，因此，基于Curvelet变换的图像ROI压缩效果更好。

图2 实验图像。A、B、C分别为Lena图像、MRI图像和细胞图像

由上述实验可知，基于Curvelet变换和SPIHT算法的ROI压缩应用于Lena测试图像效果显著，因此进一步对图2B所示MRI图像（252×252）和图2C所示细胞图像（575×575）进行压缩，并比较基于Curvelet变换和小波变换两种方法的ROI压缩效果，实验结果见图5、6和表3、4。

图3 基于Curvelet变换和SPIHT算法对Lena图像的整体压缩和ROI压缩结果比较。A～C分别为整幅图像保留0.1%、5%、30% Curvelet系数的压缩图像；D～F分别为背景部分保留0.1%、5%、30% Curvelet系数的压缩图像

图4 基于Curvelet变换和小波变换的SPIHT算法对Lena图像的ROI压缩结果。A～C分别为背景部分保留2621个、26 214个、262 144个Curvelet系数的压缩图像；D～F分别为背景部分保留2621个、26 214个、262 144个小波系数的压缩图像

由图5、6可知，在保留较少系数时，图像BG较模糊；随着保留系数的增多，基于上述两种算法的压缩图像均逐渐清晰。从表3可以看出，基于小波变换和SPIHT算法的MRI图像进行ROI压缩后的PSNR最大为41.7587 dB，而基于Curvelet变换和SPIHT算法的ROI压缩图像能无限逼近原图像；从表4可以看出，基于小波变换和SPIHT算法的细胞图像进行ROI压缩后的PSNR最大为42.7605 dB，而基于Curvelet变换和SPIHT算法的图像ROI压缩PSNR最大为97.3036 dB。因此，基于Curvelet变换和SPIHT算法的ROI压缩效果显著。

表1 基于Curvelet变换和SPIHT算法用于Lena图像压缩的性能比较（dB）

3 讨论

图5 基于Curvelet变换和小波变换的SPIHT算法对MRI图像的ROI压缩结果。ROI为MRI图像的白质，对BG灰质部分采用Curvelet变换和SPIHT算法进行压缩。A～C分别为背景部分保留2621个、26 214个、262 144个Curvelet系数的压缩图像；D～F分别为背景部分保留2621个、26 214个、262 144个小波系数的压缩图像

在进行图像压缩时，保留医学图像ROI的图像细节，而对BG采取有损压缩，这样既能不丢失重要的诊断信息，同时又能最大可能地减少数据量，这在医学领域具有重要意义和应用前景。本文将Curvelet变换和SPIHT算法相结合应用于MRI图像和细胞图像的压缩，传统的图像质量客观评价指标主要包含均方误差MSE和PSNR，两者之间的关系为PSNR＝10 lg｛[f(l,j)2max]/MSE｝，故本文选用PSNR作为客观评价指标对压缩效果进行定量分析。实验结果表明，基于Curvelet变换和SPIHT算法的ROI压缩方法能实现医学图像的高效压缩。今后研究中拟增加主观评价指标以及基于视觉感知的图像质量评价指标来定性和定量衡量图像压缩效果。

表3 基于Curvelet变换和小波变换的SPIHT算法用于MRI图像ROI压缩的性能指标比较（dB）

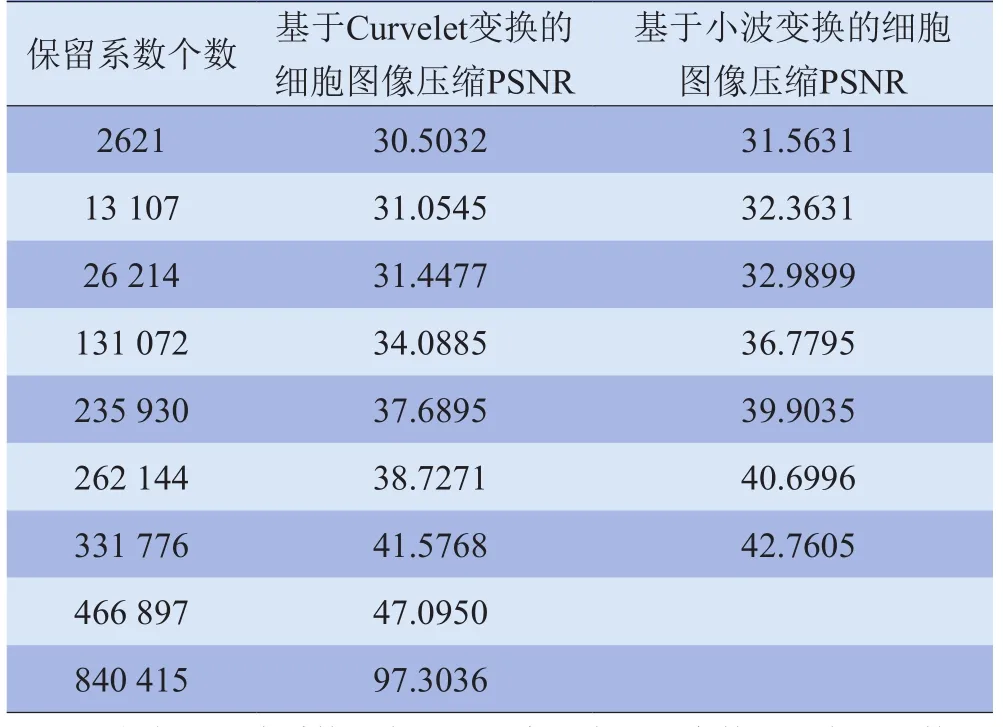
表4 基于Curvelet变换和小波变换的SPIHT算法用于细胞图像ROI压缩的性能指标比较（dB）

Curvelet变换在图像处理方面具有良好的发展态势，用较少的Curvelet系数就可以对原始图像很好地进行重建，体现了Curvelet变换在图像压缩领域的潜力。由本实验可以看出，基于Curvelet变换的ROI压缩算法更适用于医学图像压缩，但是本文算法采用人工交互方式提取ROI区域，算法效率仍待提高。今后研究方向为结合医学图像分割方法，自动探测并提取病灶，从而实现医学图像ROI的高效和自动压缩。

[1] 范金坪, 张春晓. 医学图像压缩算法研究进展. 科技信息, 2011, (25): 60, 199.

[2] David LD, Duncan MR. Digital Curvelet transform: strategy, implementation and experiments//International society for optics and photonics. Melbourne: Geoffrey I. Opat University, 2000: 12-30.

[3] Candes EJ, Demanet L, Donoho DL, et al. Fast discrete Curvelet transforms: technical report of applied and computational mathematics. California Institute of Technology, 2006, 5(3): 861-899.

[4] 武国宁, 孙娜, 段庆全. 多尺度几何分析及其在去噪中的应用. 计算机应用与软件, 2011, 28(7): 64-68.

[5] Do MN, Vetterli M. Orthonormal finite ridgelet transform for image compression. IEEE international conference on image processing, 2000, 2(27): 367-370.

[6] Maske ND, Patil WV. Comparison of image compression using wavelet for curvelet transform & transmission over wireless channel. International Journal of Scientifc and Research Publications, 2012, 2(5): 1-5.

[7] 袁芳. Curvelet变换在数字图像去噪和压缩中的研究. 西安: 西安电子科技大学硕士学位论文, 2012.

[8] Lang CS, Hong L, Li GZ, et al. Combined sparse representation based on curvelet transform and local DCT for multi-layered image compression// Communication Software and Networks (ICCSN), 2011 IEEE 3rd International Conference on Communication Software and Networks. Xi'an: Xi'an Electronic and Engineering University, 2011: 316-320.

[9] Abd-Elhafiez WM. Image compression algorithm using a fast curvelet transform. International Journal of Computer Science and Telecommunications, 2012, 3(4): 43-46.

[10] Mansoor A, Mansoor A. On image compression using digital Curvelet transform//9th International Multitopic Conference. Pakistan: National University of Computer and Emerging Sciences, 2005: 1-4.

[11] 裴营. 基于曲波变换的图像压缩算法研究. 天津: 天津师范大学硕士学位论文, 2009.

[12] Li YC, Qiu Y, Jiao RH. Image compression scheme based on curvelet transform and support vector machine. Expert Syst Appl, 2010, 37(4): 3063-3069.

[13] Reddy KN, Reddy BS, Rajasekhar G, et al. A fast curvelet transform image compression algorithm using with modifed SPIHT. International Journal of Computer Science and Telecommunications, 2012, 3(2): 1-8.

[14] 汤敏, 陈峰. 轮廓波及曲波和小波变换用于显微图像消噪的比较.中国组织工程研究与临床康复, 2011, 15(22): 4094-4097.

[15] Zhang Y, Li T, Li QL. Defect detection for tire laser shearography image using curvelet transform based edge detector. Optics & Laser Technol, 2013, 47: 64-71.

[16] 杨居义. 基于第2代Curvelet变换的彩色图像去噪. 计算机工程, 2010, 36(5): 207-209.

[17] Parmar K, Kher R. A comparative analysis of multimodality medical image fusion methods//Modelling Symposium (AMS), 2012 Sixth Asia, 2012: 93-97.

[18] AlZubi S, Sharif MS, Islam N, et al. Multi-resolution analysis using curvelet and wavelet transforms for medical imaging//2011 IEEE International Workshop on Medical Measurements and Applications Proceedings (MeMeA). Bari: Politecnico di Torino, 2011: 188-191.

[19] 赵振磊, 耿则勋, 张亚新, 等. 基于第二代Curvelet变换的自适应图像增强. 计算机工程与应用, 2009, 45(9): 192-195.

[20] 宋博, 徐超, 金伟其, 等. 基于时域和空域混合的低信噪比视频降噪算法及其分析. 红外技术, 2011, 33(8): 489-494.

[21] Said A, Pearlman WA. A new, fast, and efficient image code based on set partitioning in hierarchical trees. IEEE Transactions on Circuits and Systems for Video Technology, 1996, 6(3): 243-250.

[22] Yu Y. Improved ROI Coding Method Based on SPIHT. Nanjing: Nanjing University of Posts and Telecommunications, 2012.

[23] Wu L. Data Compression. 3rd ed. Beijing: Publishing House of Electronics Industry, 2012: 160-164.

[24] 曾琼新, 郑君惠, 谭绍恒, 等. 医学影像存档和通讯系统的临床应用研究. 中国医学影像学杂志, 2011, 19(2): 109-114.

[25] 陈威, 缑锦. 采用Haar小波与Gabor小波特征的级联式人脸检测方法. 华侨大学学报(自然科学版), 2011, 32(5): 520-524.

（本文编辑张春辉）

Medical Images Compression for Region of Interest Based on Curvelet Transform and SPIHT Algorithm

PurposeTo propose a novel compression method for region of interest (ROI) based on Curvelet transform and SPIHT algorithm.Materials and MethodsThe ROI was firstly extracted without compression, and Curvelet transform was applied for the background regions. The Curvelet coeffcients were coded using SPIHT algorithm. Then the images after compression are obtained by inverse Curvelet transform. The ROI and the background were fnally overlapped to get the full compressed image. Effect of ROI compression and overall compression were compared, as well as the Curvelet transform and wavelet transform, based on peak signal noise ratio.ResultsThe ROI compression highlighted the region of interest and the visual effect was superior to the overall compression. The peak signal to noise of Curvelet transform was higher than that of wavelet transforms, and the compressed images were more clear for the same proportion.ConclusionROI compression based on Curvelet transform and SPIHT algorithm can achieve efficient compression images without losing important diagnostic information, which complies with the requirement of high precision and high quality of medical image compression.

Data compression; Images compression for region of interest; Image coding; Algorithms; Image processing, computer-assisted; Curvelet transform; SPIHT algorithm

南通大学电子信息学院江苏南通226007

汤敏

School of Electronics and Information, Nantong University, Nantong 226007, China

Address Correspondence to: TANG Min

E-mail: tangmnt@163.com

国家自然科学基金项目（11204145）；江苏省自然科学基金项目（BK20130393）；

江苏省高校自然科学基金项目（12KJB510026）；

南通市科技项目（BK2012045）。

TP391.41

2014-03-24

修回日期：2014-07-26

中国医学影像学杂志