用小角X射线散射研究亚麻纤维分形维数与断裂强度的关系

赵 玲，王春红，李昱芃，刘家兴，郑振荣

（1.天津工业大学纺织学部，天津 300387；2.天津市纺织纤维检验所，天津 300192）

用小角X射线散射研究亚麻纤维分形维数与断裂强度的关系

赵 玲1，王春红1，李昱芃2，刘家兴1，郑振荣1

（1.天津工业大学纺织学部，天津 300387；2.天津市纺织纤维检验所，天津 300192）

用小角X射线散射法（SAXS）研究亚麻纤维的孔隙结构分形特征，并且分析亚麻纤维断裂强度与分形维数之间的关系.结果表明：SAXS是测试分形维数的一种有力工具；亚麻纤维的分形维数是2～3之间的分数，属于表面分形；亚麻纤维的分形维数与断裂强度之间的关系可以用二次曲线来拟合，拟合相关度R2能够达到0.908 6，具有很好的相关性，且亚麻纤维的断裂强度随着其分形维数的增大而减小.

小角X射线散射法；亚麻纤维；分形维数；断裂强度

1977年，法国数学家Mandelbrot首次提出分形理论（fractal theory）.分形几何学是一门以非规则几何形态为研究对象的新兴学科[1-2]，分形的原意是不规则的、分散的、支离破碎的，具有自相似性、无标度性和自仿射性[1].1984年，Mandelbrot首次将分形理论用于材料研究；1993年，龙期威在分析了大量实验的基础上，提出了材料中的多度域分形[1].此后，分形理论在材料科学中的应用越来越多，主要用来研究材料的韧性、断裂韧性、磨损、强度、界面等方面[1-2].成志芳等[3]研究了Al/Ni-YPSZ复合涂层力学性能与分形维数的关系，用二次曲线拟合所得结果，结果表明材料的断裂强度随分形维数的增大先减小后增大.章冠人[4]研究了韧性和脆性断裂的分形维数，指出在韧性断裂中，材料的断裂韧性随分形维数的增大而减小；在脆性断裂中，材料的断裂韧性随分形维数的增大而增大.天然植物纤维中有孔隙存在，纤维的多孔结构对纤维的物理性能有着很大的影响，如吸湿、隔音、强度等[5-6].孔隙结构的分形维数可以定量描述孔隙结构的复杂程度，孔隙结构的分形维数是介于2～3之间的分数，分形维数越接近2，表明孔隙结构越均匀；分形维数越接近3，表明孔隙结构越复杂[1，7].分形维数的计算方法有很多，其中经典的有自相似维数和盒计数维数等.小角X射线散射（SAXS）是测定维数的一种新的方法[1-2，8]，本文用SAXS技术测试了亚麻纤维的分形维数，该方法对材料无损伤，对测试环境条件无要求，测试时间短，得到的试样信息是统计的结果[8]；在此基础上分析了亚麻纤维的断裂强度与其分形维数之间的关系，并建立关系模型，为有效预测纤维的断裂强度提供一定的理论指导.

1 实验部分

1.1 实验样品

实验选用6种不同产地、不同脱胶方式的亚麻纤维，其详细信息如表1所示.

表1 实验样品介绍Tab.1 Introduction of experimental sample

由表1可知，亚麻纤维经沤麻处理后，在纤维长度相同的情况下，纤维细度越细，其沤麻效果越好.

1.2 亚麻纤维分形维数测试

本实验在上海同步辐射光源X射线小角散射线站（SAXS）完成，其设备能量可达20 keV，能量分辨率为6×10-4@10 keV，光子通量为1011S-1@10 keV，最小可测量角度为0.023°，测试时样品到探测器距离为5 m，入射X射线波长为0.124 nm.以束纤维进行实验，曝光时间为50 s.

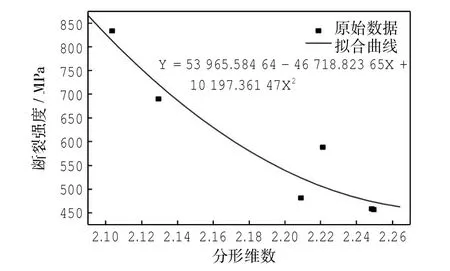
测试所得原始数据经FIT2D软件转换为I（q）-q原始数据，散射强度 I实际=I样品-K*I背底，K=作出I（q）-q的双对数ln I（q）-ln q曲线图（I（q）为实际散射强度intensity；q为散射矢量；θ为散射半角；λ为入射X射线波长）.在ln I（q）-ln q图中，求最接近直线的线段的斜率-a，由Porod公式I（q）=Ie（ρA-ρB）2给出I（q）∝q-a.式中：a为与分形维数有关的参数，也称Porod斜率，若3

1.3 亚麻纤维强度测试

采用美国英斯特朗公司制造的万能强力机，根据标准ASTMD3822-07[9]，在标准大气压下测试亚麻纤维的断裂强度，测试时隔距为25.0 mm，速度为5 mm/ min，每种纤维测试30组.

2 结果与讨论

2.1 亚麻纤维分形维数分析

图1—图6所示为1～6组亚麻纤维的lnI（q）-lnq图中最接近直线部分的直线拟合图，其拟合相关度分别为0.999 2、0.999 4、0.999 7、0.999 5、0.999 9、0.999 8，都有极好的线性相关性.

图1 1号样品ln I（q）-ln q图Fig.1 ln I（q）-ln q figure of sample 1

图2 2号样品ln I（q）-ln q图Fig.2 ln I（q）-ln q figure of sample 2

图3 3号样品ln I（q）-ln q图Fig.3 ln I（q）-ln q figure of sample 3

分别求出图1—图6中拟合的直线的斜率，如表2所示.可以看出，1～6号纤维中，3

图4 4号样品ln I（q）-ln q图Fig.4 ln I（q）-ln q figure of sample 4

图5 5号样品ln I（q）-ln q图Fig.5 ln I（q）-ln q figure of sample 5

图6 6号样品ln I（q）-ln q图Fig.6 ln I（q）-ln q figure of sample 6

综上所述，6组试样的线性拟合效果均较好，验证了亚麻纤维的孔隙结构符合分形理论；亚麻纤维的分形维数是2～3之间的分数，且亚麻纤维的沤麻效果越好，其分形维数越大，说明沤麻效果越好，亚麻纤维的孔隙结构越复杂.

2.2 纤维断裂强度与分形维数的关系

材料的力学性能与其分形维数有一定的关系，不同的断裂方式（如韧性断裂和脆性断裂），其断裂强度与分形维数的关系也不尽相同[3-4，10-18].表3所示为6组亚麻纤维强度的测试结果.

表3 亚麻纤维断裂强度测试结果Tab.3 Results of breaking strength of flax fiber

对亚麻纤维的分形维数和对应的断裂强度用二次曲线进行拟合，如图7所示，得出拟合二次函数为Y=53 965.58-46 718.82X+10 197.38X2，拟合相关度R2为0.908 6，相关度很好.

图7 亚麻分形维数与断裂强度的关系拟合图Fig.7 Fitting relationship between fractal and breaking strength of flax fiber

由图7可以看出，随着亚麻纤维孔隙结构分形维数的增大，亚麻纤维的断裂强度减小.这是因为随着亚麻纤维孔隙结构分形维数的增大，纤维的孔隙结构比较复杂，孔的形状、大小、分布不均匀严重，这样就使得纤维在拉伸过程中受到的拉力不能均匀地分散，导致断裂强度降低[1].

3 结论

（1）SAXS是研究亚麻纤维分形特征的有力工具，用SAXS测试分形维数，对材料无损伤，对测试环境条件无要求，测试时间短，得到的试样信息是统计的结果，而传统的方法只能得到局部试样的信息.

（2）亚麻纤维孔隙结构的分形维数是2～3之间的分数，沤麻效果越好，亚麻纤维分形维数越大，其孔隙结构越复杂.

（3）亚麻纤维孔隙结构的分形维数与其断裂强度and its applications to batch fabrication of SPM tip arrays[J]. Microelectronics Journal，2005，36（7）：678-682.

[4] CHOI W B，JU B K，LEE Y H，et al.Silicon to indium inoxide coated glass bonding for packaging of field emission arrays fabricated on silicon wafer[J].Journal of Materials Science，1999，34（19）：4711-4717.

[5] JAGTAP V S，MINOT C.Internally integrated active-type patch antenna for semiconductor superlattice THz oscillators[J]. Terahertz Science and Technology，IEEE Transactions on, 2012，2（1）：131-136.

[6]ORIHASHI Naoyuki，HATTORI Shinnosuk，SUZUKI Safumi，et al.Experimental and theoretical characteristics of terahertz oscillations of resonant tunneling diodes integratedwith slot antennas[J].Janpanses Journal of Applied Physics，2005，44（11）：7809-7815.

[7] 张文锦，李建雄，毛陆虹.基于多波束切换的便携式RFID阅读器设计[J].天津工业大学学报，2013，32（1）：52-56.

[8] 马建欢，李建雄，肖康，等.太阳能电池作为天线辐射体的RFID标签天线的设计[J].天津工业大学学报，2013，32（1）：57-60.

Relationship between fractal dimension and breaking strength of flax studied by small angle X-ray scattering

ZHAO Ling1，WANG Chun-hong1，LI Yu-peng2，LIU Jia-xing1，ZHENG Zhen-rong1
（1.Division of Textiles,Tianjin Polytechnic University,Tianjin 300387,China；2.Tianjin Textile Fibre Inspection Institute,Tianjin 300192,China）

The small angle X-ray scattering(SAXS)is used to study the fractal of flax fiber pore structure,and the relationship between the breaking strength and fractal dimension of flax fiber is analyzed.The results show that SAXS is a powerful tool to test the fractal dimension；the fractal dimension of flax fiber is 2-3 which is surface fractal；the relationship between the breaking strength and fractal dimension of flax fiber can be fitted by a quadratic curve,the fitting correlation coefficient R2is 0.908 6 and has a good correlation,and the breaking strength is anti-related with fractal dimension.

SAXS；flax fiber；fractal diminsion；breaking strength

TS101.1；TS102.221

A

1671-024X（2014）01-0025-04

2013-06-06

天津市自然科学基金重点项目（11JCZDJC22300）；中国纺织工业协会科技指导性项目（2008026，2012002）

赵 玲（1988—），女，硕士研究生.

王春红（1980—），女，副教授，硕士生导师.E-mail：cn_wangch@163.com