超高层建筑表面风荷载数值模拟研究

孔德坤，樊 佳

（中机中联工程有限公司，重庆400039）

超高层建筑表面风荷载数值模拟研究

孔德坤，樊 佳

（中机中联工程有限公司，重庆400039）

该文通过计算流体力学数值模拟技术对某超高层建筑进行了表面风荷载分布的数值模拟。结果表明：由于漩涡脱落，在结构侧面边缘出现了较强烈的负压区；在周边建筑干扰高度范围内，结构表面风压分布较混乱，结构在干扰高度以上部分风压分布比较规律；局部部位的设计风压应参考各风向角下风压峰值。

计算流体力学；数值模拟；风荷载；局部体型系数；超高层建筑；风荷载

近年来，随着科技的进步与人口的剧增，超高建筑得以迅速发展。现代高强轻型的建筑材料以及先进的施工技术，使得超高层建筑愈发轻柔，进而成为了风敏感建筑，风荷载成为其控制荷载。因此精确、有效地分析超高层建筑表面风荷载分布成为了近几年的研究热点问题。

超高层结构表面风荷载的研究手段有风洞试验、现场实测和数值模拟[1]。随着计算流体力学的理论和计算机技术的不断发展，风荷载数值模拟研究在结构工程领域得到了广泛的应用[2]。较之风洞试验，风荷载数值模拟有很多优势：具有模拟真实条件的能力，周期短，成本低；数据全面，数据后处理方便、直观，便于研究人员分析与参考。本文采用计算流体力学方法，对某超高层结构表面风荷载分布进行计算，为该结构的风振响应计算提供计算基础。

1 计算流体力学概述

1.1 计算流体力学定义

计算风工程（Computational Wind Engineering，CWE）又称数值风洞，是结构风工程的一种重要手段。计算风工程的核心是计算流体动力学[3-7]（Computational Fluid Dynamics，CFD），用计算机技术和离散数值方法来近似模拟流动现象并获得由流体产生的作用力的一种技术。

1.2 流体力学基本控制方程

1.2.1 质量守恒方程

质量守恒方程又称为连续方程，任何流体流动问题必然满足连续方程。根据这一定律，可以得出质量守恒方程[7]：

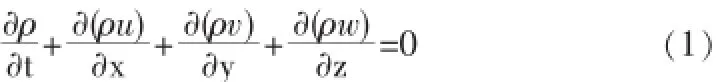
令div(a)=∂ax/∂x+∂ay/∂x+∂az/∂x，式（1）可以写成：

上式中，ρ为流体的密度；t为时间；u为速度矢量，u、v、w为速度矢量u在x、y、z方向的三个分量。

1.2.2 动量守恒方程

动量守恒定律定律实质上是牛顿第二定律，也是任何流动问题必须满足的基本定律。这一定律可以导出三个方向的动量守恒方程，其表达式为[7]：

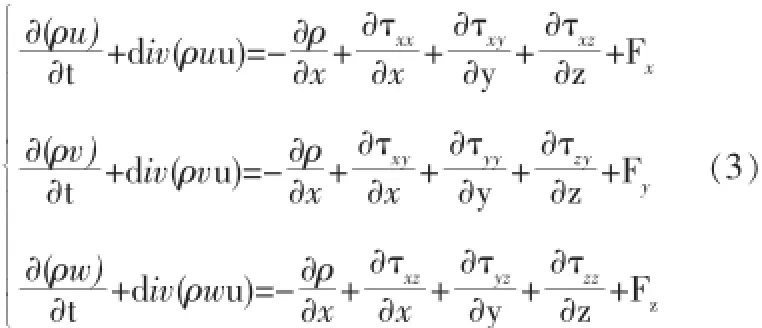
上式中，p为粒子外压力；τxx、τxy和τxz是作用在粒子表面上的粘性应力；Fx、Fy和Fz是粒子整体上的体力，式（3）是对牛顿流体和非牛顿流体均成立的动量守恒方程。风工程中的低速风一般可看作是牛顿流体，其粘性应力τ与流体的变形率成比例，将牛顿流体的本构关系代入到动量守恒方程式（3）中，得到牛顿流体的运动方程，该方程称为纳维-斯托克（Navier-Stokes）方程，也称为运动方程，其表达式如下：

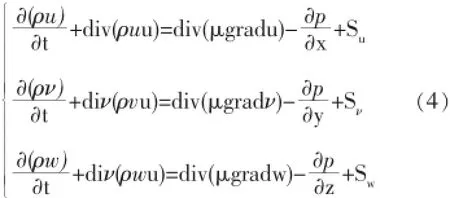
1.3 控制方程的离散及求解

1.3.1 有限体积法

控制方程的离散方法分为有限差分法、有限元法和有限体积法。有限体积法的基本思路为：把计算区域划分为有限多个不重叠的子区域，得到计算网格，然后确定各个子区域的节点位置和节点对应的积分体积；进而将待求解的流体力学控制方程对各个控制体积进行积分，从而建立起离散方程组。

1.3.2 离散方程的数值求解

用有限体积法等离散方法建立的离散方程组，一般不能直接用来求解，需对离散方程进行调整，并对各未知量（速度、压力等）的求解方式进行特殊处理。应用最广泛的是半隐式方法（SIMPLE算法）其基本思想为：根据给定压力场，求解离散化的动量方程，得到速度场。需要注意的是，对这个速度场应进行修正。修正的方法是将离散化的动量方程所得到的压力与速度的关系代入离散化的连续方程，求出修正的压力值，进而又求出新的速度场，重复此计算直至收敛。

2 工程介绍

本文的研究依托于重庆某超高层商业中心项目，该商业中心由一栋超高层酒店办公综合楼、一栋超高层办公楼及一座多层商业裙房组成。其中，1号塔楼为酒店办公综合楼，结构计算高度为270m，最高层数为60层；2号塔楼为办公楼，其结构计算高度达到150m，商业裙房地上5层地下4层。整个商业中心属于超高层建筑群。建筑物整体和局部位置风荷载的取值缺乏规范依据。因此，对该结构进行风荷载数值模拟就显得尤为必要。

3 计算模型的建立

3.1 流体模型与网格划分

流场模型的尺寸主要取决于其边界是否对结构模型的结果产生影响。一般要求结构迎风面距流场入口4倍结构高度，结构背风面距流场出口8倍的结构高度，以使湍流能够充分发展。对于本文研究超高层，流场的高度可以取3～4倍的结构高度，流场水平宽度不小于8倍结构宽度，并且阻塞率控制在3%以内。

在计算流体动力学模拟中，网格尺度和网格质量对计算精度和计算效率有重要影响。由于建筑表面区域和尾流区域流动变化比较剧烈，因此对建筑表面以及尾流区域进行网格加密，其他区域按照一定的梯度逐渐增大网格的尺寸。几何模型与网格划分如图1所示。

图1 建筑几何模型与网格划分

3.2 湍流模型与边界条件

本文数值模拟时地貌类型取为C类，基本风压0.45 kN/m2。计算流域的进口边界为速度入口边界，依据规范的平均风速剖面和湍流基本参数，通过用户自定义函数（UDF）以动态方式加载到FLUENT求解器中。计算流域的出口边界为压力自由出流条件。计算流域的两侧和顶部采用对称边界条件，等价于自由滑移的壁面。结构模型的表面和地面都采用无滑移边界条件。湍流模型采用标准k-ε模型。

4 数值模拟结果

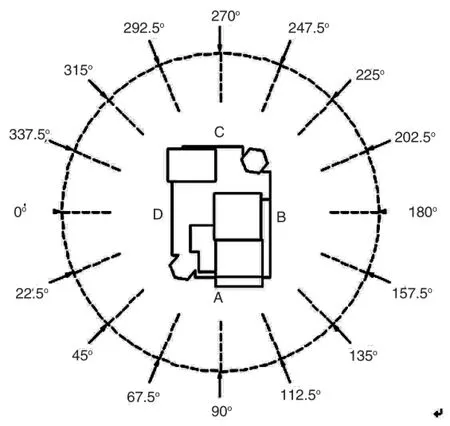
图2 各工况风向角示意图

模拟计算了有周边建筑影响时100年重现期风荷载作用下的工况，该工况下又分别计算了16个风向角，以每22.5°为一个自工况。

需要注意的由于篇幅原因，且重庆地区主导方向为北风，对应的试验工况为风向角270°，故本文仅列出该工况下模拟结果并进行分析。

迎风面上由于遮挡建筑的存在，风荷载体型系数变化幅度较显著，其中轴线位置受到来流的垂直撞击，体型系数较大；1号塔在建筑2/3高度处的正面停滞点局部体型系数达到最大值；2号塔由于楼高小于1号塔，正面停滞点的体型系数最大值不到0.8。当来流撞击至建筑迎风面时，气流会从滞点向迎风面各边扩散，使得体型系数由迎风面中心区向各边界逐渐减小。1号塔顶部迎风面存在体型的收进，在收进部分有流动分离以及柱涡出现，使得这部分迎风面受到吸力而非压力。在建筑侧风面、背风面以及顶面，局部体型系数皆为负值，其峰值出现在建筑的各角部。侧风面与背风面后缘的局部体型系数分布比较均匀。在主楼与裙房交界处，由于有体型的突变，造成了侧风面角部出现了较大的吸力，局部体型系数可以达到近-1.0。

将图3与图4之中1号塔表面平均风压系数分布作对比，可以直观地看出，由于周边建筑的存在，造成了其迎风面体型系数分布在干扰高度内产生较大变化。

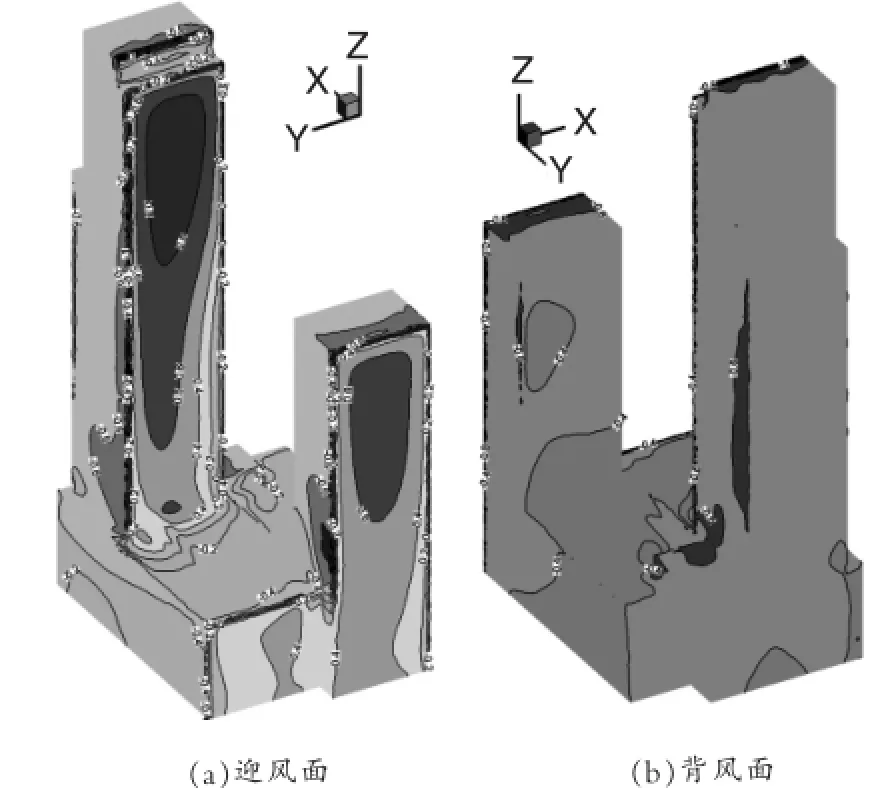
图3 270°风向角有周边建筑

5 结论

本文运用计算流体动力学软件Fluent对某超高层及其周边建筑100年重现期风荷载作用下，建筑表面风压值模拟，可得出以下结论：

图4 270°风向角无周边建筑

（1）该结构塔楼表面风压分布，于风向垂直于建筑表面时风压较大，在侧面边缘由于涡旋脱落，出现了较强烈的负压，其绝对值甚至超过了最大正压绝对值，应该在建筑表面幕墙设计时引起注意。

（2）该结构与周边建筑距离很近，在周边干扰建筑高度范围内干扰作用比较明显，塔楼高出周边建筑高度以上部分风压分布比较规律。在周边建筑干扰下目标建筑表面风压分布图中可以看出，风压绝对值却在局部有所加强。

（3）局部部位的设计风压可参考各风向角下的风压绝对值最大值进行。

[1]Theodore Stathopoulos.Computational wind engineering: Past achievements and future challenges[J].Journal of Wind Engineering and Industrial Aerodynamics，1997（67、68）:509-532.

[2]谢壮宁，方小周，倪振华.超高层建筑的等效静风荷载-扩展荷载响应相关法[J].振动工程学报，2008，21（4）:398-403.

[3]周雪漪.计算水力学[M].北京:清华大学出版社，1995.

[4]陶文铨.数值传热学[M].第二版.西安:西安交通大学出版社，2001.

[5]郭鸿志.传输过程数值模拟[M].北京:冶金工业出版社，1998.

[6]P.Rollet-Miet，D.Laurence，J.Ferziger.LES and RANS of turbulent flow in tube bundles[J].International Journal of Heat and Fluid Flow，1999，20（3）:241-254.

[7]H.K.Versteeg，W.Malalasekera.An Introduction to Computational Fluid Dynamics:The Finite Volume Method[M]. Wiley，New York，1995.

责任编辑：孙苏

Study on Computational Simulation of Surface Wind Load of High-rise Buildings

The surface wind pressure distribution of a super high-rise building is simulated numerically through computational fluid dynamics numerical simulation technology.The results show that a negative pressure region appears at the side of the structure because of vortex shedding,the surface wind pressure distribution on the super high-rise building is in disorder within the range of the interference height of surrounding buildings,but the wind pressure is regularly distributed when the structure is above the interference height,and the wind pressure peak value at different wind directions should be referenced in structure design to determine the local wind pressure.

computational fluid dynamics;numerical simulation;wind load;local shape coefficient;high-rise building

TU973+.213

A

1671-9107（2014）11-0056-03

10.3969／j.issn.1671-9107.2014.11.056

2014-09-25

孔德坤（1983-），男，安徽亳州人，研究生，工程师，主要从事结构设计工作。