mBBM方程的含椭圆函数形式的精确解*
2014-03-06刘转玲
刘转玲
(兰州商学院信息工程学院,甘肃兰州 730020)
引言
非线性偏微分方程是数学的一个非常重要的分支,常被用来描述过程控制、生态系统、经济系统、化学循环系统和流行病学等问题.非线性偏微分方程描述上述问题能充分考虑到时间、空间、时间延迟及其他因素,所以更准确地反映了现实情况.
Benjamin -Bona- Mahony 在水波研究中提出了 BBM 方程[1,2],之后发展为 mBBM[3]方程,这个方程是弱非线性色散介质中长波单向传播的重要模型,因而,对于mBBM方程的深入研究[4],特别是对于有效地数值计算方法的研究,具有重要的理论和现实意义.
本文的目的是应用Painlevé直接截断法对mBBM方程的精确求解作深入的探讨.
1 直接截断方法简解
Painlevé直接截断方法[5,6]是将Painlevé检验中的Laurent级数做有限截断,其中假定奇性流形函数是具有某种特定的性质,最后,偏微分方程的精确解是通过确定截断级数的系数来确定.这一方法简洁直接,在一定范围内具有相当的普适性.Painlevé直接截断方法简述如下.
对于给定的偏微分方程:

式中U(x,t)是一个关于x,t的多项式.假设方程(1)具有

2 椭圆函数的性质
如果f(ξ)和g(ξ)满足以下椭圆函数的条件:
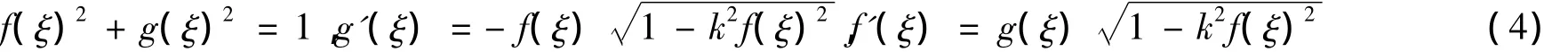

3 mBBM方程的含椭圆函数形式的精确解


4 结论
运用Painlevé直接截断法,不仅可以求出mBBM方程的其他一些不同形式的精确解,也可求出其他一些偏微分方程的精确解.
[1]洪宝剑,卢殿臣,赵康生.Burgers-BBM 方程新的精确解[J].应用数学,2007,20(1):134 -139.
[2]汪裕才.周期边界条件下B-BBM方程的整体吸引子[J].应用数学,2004,17(2):239-242.
[3]陈松林,侯为根.推广的B-BBM方程和B-BBM方程的显式精确解[J].物理学报,2001,50(10):1842-1846.
[4]郭鹏,张磊,王小云,等.mBBM 方程和Vakhnenko方程的显示精确解[J].量子电子学报,2010,27(6):683-686.
[5]Zhao D,Luo H G,Wang S J,et al.A direct truncation method for finding abundent exact olutions and application to the one -dimensional higher- order Schrodinger equation[J].Chaos Solitons and Fractals,2005,24:533 -547.
[6]Zhao D,Luo H G,Chai H Y.Integrability of the Gross- Pitaevskii equation with Feshbach resonance management[J].Phys.lett.A,2008,372:5644 -5650.
[7]王明亮,李志斌,周宇斌.齐次平衡原则及其应用[J].兰州大学学报:自然科学版,1999,35(3):8-16.
