光伏电池铺设倾角的动态优化与分析

赵心旭，丁少婷，王义康

(1.中国计量学院 量新学院，浙江 杭州 310018;2.中国计量学院 理学院，浙江 杭州 310018)

太阳能小屋是通过在建筑物外表面铺设光伏电池，将产生的直流电经过逆变器转换成220 V 交流电供家庭使用，并将剩余电量输入电网。不同种类的光伏电池每峰瓦的价格差别较大，且每峰瓦的实际发电效率或发电量还受诸多因素的影响。对于光伏电池板铺设倾角的研究，国内外学者已做了一些有益的探索，刘祖明等人提出在确定最佳倾角时应综合考虑方阵面上太阳辐射照度的连续性、均匀性和极大性［1］;Sun Jianping 考虑在有遮挡影响的情况下，对光伏电池等间距架空铺设模式进行了研究，并用PVSYST 进行了仿真计算［2］;李实等人针对光伏组件的摆放和不同阵列的间距进行了计算和分析［3］;朱超群等人在散射辐射各向同性的假定下，推导出了南向倾斜面上平均太阳总辐射的最佳倾角公式［4］;杨金焕等人针对均衡性、季节性、临时性3 种负载的特点，根据Hay 的天空散射辐射各向异性的模型，计算了倾斜面上的太阳辐射照量，给出了夏季型、冬季型负荷的参考倾角［5］。从已有的研究来看，主要集中在特定安装条件、光照面积、辐射量等因素下固定倾角的优化，忽略了由于不同太阳辐射量下对应的最优倾角连续变化所带来的影响。

对于特定区域，不同季节气候条件下，太阳直射角有所不同;而对于特定的光伏电池，单位面积时间内接受到的辐射量将直接影响其发电量。因此在太阳能小屋设计中，研究光伏电池板随时间变化的最佳倾角问题，对于太阳能小屋的最优设计具有一定的实际意义和实用价值。

1 倾斜面上的太阳辐射强度模型

对于一个倾斜面上所能接受到的太阳辐射量主要包括直射辐射量、散射辐射量和地面反射辐射量［6］3部分。其模型公式如下

其中，Ib为直射辐射量;Id为天空散射辐射量;Ig为地面反射辐射量，分别对3 类辐射进行计算。

图1 单个电池板方位角与倾角示意图

其中，α 为倾斜面与水平面的夹角;θ 为太阳光的入射角，即太阳辐射光线与屋顶表面的夹角;γ 为斜面方位角，表示太阳光线的水平投影偏离正南方向的角度，取正南方向为起始点，向西为正，向东为负。模型计算中还需要用到时角ω、赤纬角δ 及当地纬度值φ，其中赤纬角指的是地球赤道平面与太阳和地球中心连线之间的夹角。

1.1 直射辐射量的计算

考虑直射辐射量Ib，当倾斜面与水平面的夹角为α 时，太阳光的入射角度θ 满足表达式

将正午12 时的时角记为0°，每1 h 为15°，正午12 时前记为负值，正午12 时后记为正值，如上午10时和下午14 时可分别为－30°和30°。则时角的计算公式为

式(3)中ts为太阳时。

赤纬角δ 即为太阳直射纬度，其计算公式为

式(4)中n 为日期序号。记1 月1 日为n=1，则3 月22 日对应为n=81。当α=0，γ=0 时，可得水平面的太阳光入射角为

从而得到倾斜面和水平面上接受到的直射辐射分别为Ib=Incosq 和Ib0=Incosq0，其中In为垂直于太阳光线平面上的直射辐射强度。由此根据上述可得倾斜面上直射辐射量为

1.2 散射辐射量的计算

对于散射辐射Id，根据RAY 异质分布模型［7］可知倾斜面上辐射量是由太阳光盘的辐射量和其他天空穹顶均匀分布的散射辐射量两部分组成，计算公式可表示为

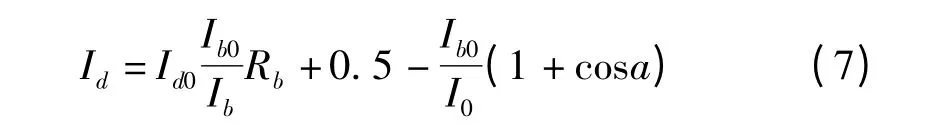
其中，Id0为水平面散射辐射强度;Rb为倾斜面上与水平面上直射辐射量之比为大气层外水平面太阳辐射，可由式(8)确定。

其中，Isc为太阳常数，由文献［8］取为1 353 W·m－2;w0为水平面上日落时角，由w0=arccos(－tanj tand)确定。

1.3 地面反射辐射量的计算

对于地面反射辐射而言，可根据Lambert 定律［9］，将地面的反射辐射看成是各向同性的，可计算得到

其中，ρ 为地面反射率，根据当地的实际情况，近似取0.2。

根据上述式(6)～式(7)和式(9)的分析，得到倾斜面上的太阳辐射强度为

2 随太阳能辐射量变化的优化模型

电池板的朝向与倾角直接影响光伏电池对太阳能的吸收量，由于地球公转和自转的影响，在实际中每时刻的单位面积接受到的太阳辐射量都在变化，与之相应的太阳能光伏电池铺设最佳倾角也随之变化，因此有必要对最优倾角进行动态分析。

设一年内第n 天t 时刻的赤纬角为δn，时角为wt，I(n，t)为斜面上的太阳辐射强度，Iv(n，t)为垂直于太阳光线平面上的直射辐射强度，Iw(n，t)为水平面总辐射强度，Is(n，t)为水平面散射辐射强度，cosθ(n，t)为第n 天第t 时对应的倾角，一年按365 天记，则有

令

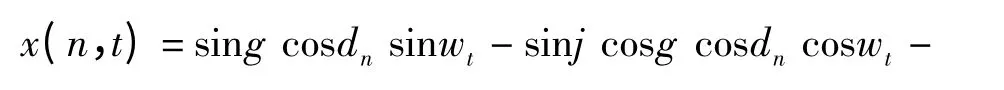
则有cosq(n，t)=x(n，t)sina+y(n，t)cosa，整理得

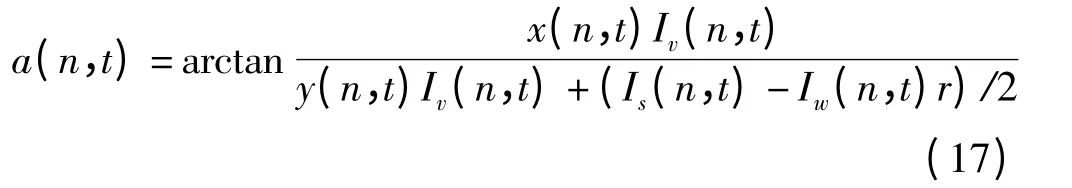
将式(17)代入式(16)可得到，第n 天t 时刻的最优倾角对应的太阳辐射量的最大值I(n，t)为

则一年最大的太阳总辐射量为

将离散的数据连续化，可得n 天t 时刻内斜面可接收的最大辐射量I 为

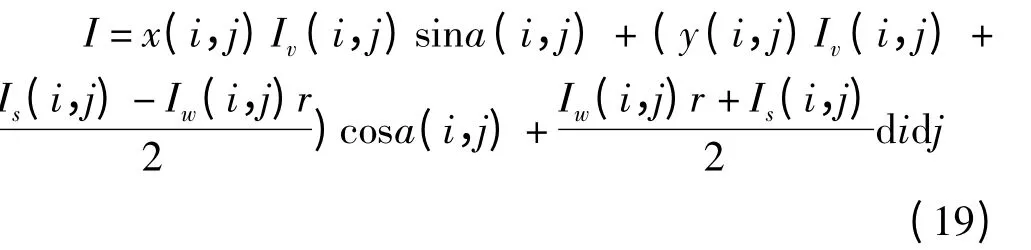
其中，积分上限n 代表积分研究的是从初始测量第0天到第n 天的辐射总量，一般年辐射量以该年1 月1 日为第0 天，n 的取值范围为［0，365］;t 则代表积分研究的是从第0 时刻到t 时刻的辐射总量，一般以0点(12 时)为第0 时刻，t 的取值范围为［0，23］。

3 仿真计算

将某市2010 年全年气象数据，代入式(10)，对于光伏电池板不同的安装倾角，可得到单位面积上当倾角发生改变时辐射量的变化情况。当地纬度值φ 取40.1°，计算时固定倾斜角θ，使其从0°变化到90°，由式(10)可得不同固定倾角下对应的辐射量值，进行比较从而可确定辐射量最大时的倾斜角即为全年最优固定倾角。通过Matlab 进行求解，得到总辐射量随不同固定倾角的变化情况如图2 所示。

图2 南向倾斜角与总辐射量关系

根据计算结果可知，随着倾斜角的变化辐射量先增加后减小，在某点处达到最大，辐射量最大时对应角度为37.9°，即该市安装光伏电池板的年最佳固定倾斜角度为37.9°。按此角度放置光伏电池板，则单位面积在一年内可接收到基于固定倾角的最大辐射量。

对于动态变化倾角，由式(19)可知优化模型中最佳倾角是随着时间连续调整，而考虑到在现实生活中气象数据的采集是以每个小时为测量单位，不能做到完全实时监控太阳辐射量。因此为简化计算和便于实际应用，本文首先以月为测量单位，计算每月对应的固定最优倾角。天数由0 变化到365，时刻的大小由0 变化到23，代入式(17)，可得到某一个月可接收的总辐射量对应的最大倾角，然后将最优倾角代入式(18)，得到此月最优倾角时对应的太阳辐射量。该市2010年的月最优倾角及其对应辐射量如表1 所示，最优倾角及其对应辐射量变化趋势如图3 和图4 所示。

表1 某市月最优倾角及其对应辐射量 MJ·m－2

图3 最优倾角随月份变化趋势图

图4 太阳辐射量随月份变化趋势图

该市各月地面接受太阳辐射整体近于正态分布，最高点出现在夏季，而总辐射量较低的月份普遍出现在冬季，特别是11 和12 月份，月辐射量变化与太阳赤纬角的变化规律基本吻合。但由于当年2 月份天气普遍晴朗，所接收到的太阳辐射量较其他月份更大，与理论有一定偏差。其次，不同月份最佳倾角有一定波动，这主要是由于太阳直射辐射与散射辐射比值的不同，直射辐射比重越大。最佳倾角越接近于赤纬角与地理纬度的和，散射辐射比重越大。。通过计算，月最佳倾角趋近于37.7°，全年接收总辐射量为988 976.26 MJ·m－2。对于分时间段使用的平板型太阳能集热器或光伏系统应根据月份动态调整其最优倾角，获得太阳辐射能较全年固定倾角下的辐射能显著增加。

为进一步优化上述模型，文中对365 天内每天的最优倾角情况进行分析。以天为测量单位，计算每天对应的最优倾角。将天数n 固定，时刻t 在0 ～23 变化，代入式(17)，可得到某一天可接收的总辐射量对应的最大倾角，然后将最优倾角代入式(18)，得到每天最优倾角以及其对应的太阳辐射量。该市2010 年的365 天每天最优倾角及其对应辐射量变化趋势如图5和图6 所示。

图5 最优倾角随月份变化趋势图

由图5 和图6 可知，日最优倾角相较于月最优倾角波动变化不大，日辐射量在冬季普遍偏低而夏季普遍较高，但由于受季节和天气影响，特别是阴雨天的出现，日辐射量会出现一定程度的波动。日固定最优倾角条件下，全年接收的太阳总辐射量为1 730 992.11 MJ·m－2，与月固定最优倾角相比，全年接收的太阳能总辐射量增加57.13%。

图6 太阳辐射量随月份变化趋势图

4 结束语

通过建立以单位面积全年接收的太阳能总辐射量最大为目标，随光照辐射强度变化的光伏电池板最佳铺设倾角动态优化模型，得到光伏电池板铺装的动态最优倾角。从对该市气象数据研究中发现，月最优倾角变化符合太阳赤纬角的变化规律。根据仿真计算和分析，以日固定最优倾角为条件，结果表明，按日调整最优倾角比全年固定和按月固定最优倾角下的可接收的太阳辐射增加显著。本文模型的研究基于最优倾角的连续实时变化，考虑到实用性，在仿真计算时按日计算并与全年月固定倾角的计算结果进行了对比研究，如果考虑实时更新，动态自适应调整倾角，则会获得更高的太阳辐射量。对于太阳能光伏电池板铺设倾角的动态实时调整，则需要根据产品成本和现场实用性等，做进一步深入研究。

［1］ 刘祖明，廖华，李耀飞，等.固定式光伏方阵最佳倾角［J］.太阳能学报，1992，13(4):385－388.

［2］ SUN Jianping.An optimum layout scheme for photovoltaic cell arrays using PVSYST［C］.Proceeding of Mechatronic Science，Electric Engineering and Computer，2011:243－245.

［3］ 李实，田春宁，鞠振河，等.光伏系统的优化设计［J］.沈阳工程学院学报:自然科学版，2011，7(4):107－110.

［4］ 朱超群，廖静明.我国最佳倾角的计算及其变化［J］.太阳能学报，1992，13(1):38－44.

［5］ 杨金焕，葛亮，陈中华，等.季节性负载光伏方阵的倾角［J］.太阳能学报，2004，24(2):241－24.

［6］ 方荣生.太阳能应用技术［M］.北京:中国农业机械出版社，1985.

［7］ 贾友见，聂林如，黄仕华.计算水平地面散射辐射量的模型［J］.昆明理工大学学报:自然科学版，2000，25(5):40－42.

［8］ 申政，吕建，杨洪兴，等.太阳辐射接受面最佳倾角的计算与分析［J］.天津城市建设学院学报，2009，15(1):61－64.

［9］ 谭昌伟，王纪华，黄义德，等.运用光谱技术改进Beer－Lambert 定律的定量化及其应用研究［J］.中国农业科学，2005，38(3):498－503.