基于匀速直线运动下模糊图像复原的研究

盛文正，唐国红

(长沙理工大学 电气与信息工程学院，湖南 长沙 410114)

在获取摄影图像的过程中，由于摄影设备或摄影对象在曝光瞬间产生相对运动，从而使获得的图像呈模糊状态。运动模糊图像的复原是指在研究图像退化原因的基础上，以退化图像为依据，根据一定的先验知识来建立一个退化模型，再根据逆向推理，来恢复原始图像。在运动中，无论是变速直线运动还是曲线运动，其在一定条件下均可视为由许多分段的匀速直线运动构造而成。因此，对匀速直线运动模糊图像的复原的研究有重要意义［1］。运动图像复原在整个图像研究中占有重要地位，其可运用于天文、医学、交通、军事及刑侦等领域。在早期图像复原研究中有较多的方法得以运用，例如:以逆滤波、维纳滤波为代表的频域复原、小波域图像复原和基于贝叶斯图像复原等［2］。

在图像复原的过程中，对于点扩散函数(Point Spread Function，PSF)有两种情况，第一种是已知全部或部分点扩散函数;第二种是未知点扩散函数。而在实际生活中，图像在获取时由于其他原因而使获得的图像是模糊图像。在这种情况下，点扩散函数在通常情况下均是未知的。若知道点扩散函数的模糊长度和模糊方向，则可用前面的一些方法来进行图像复原。因此，提出一种有效的方法来鉴别点扩散函数的参数对于运动模糊图像复原来说是必要和迫切的问题。在针对模糊角度的确定时，陈前荣，李均利等人均提出或改进了模糊角度的计算算法，而本文也对运动模糊图像提出改进的模糊方向算法和模糊尺度的计算算法［3－4］。对于维纳滤波而言，K 值的精确与否直接影响到模糊图像的复原效果。通常情况下，大多数研究者采用的方法是运用先验知识来确定K 值，或通过大量仿真来缩减K 值的范围，再找出仿真效果较好的值，这类方法计算量较大，实际操作步骤较多，目前对K 值确定的最佳方法是采用K 值自动估计法，在本文中，也对该方法做了部分改进。

1 运动模糊图像复原退化模型

运动模糊图像复原处理建立在图像复原的数学模型基础上。在实际图像获取中，由于使图像退化的原因较多，因此需要在图像复原处理的过程中，将整个退化模型看作是一个线性系统的退化过程，并将退化原因视为线性系统退化的一个原因来对待，则可建立一个运动模糊图像复原的退化模型，因此来分析图像退化的过程。如图1 所示。

图1 图像退化及复原模型图

根据图1 可知，退化图像时间域的表达式为

其中，g(x，y)为运动模糊图像;h(x，y)为退化函数的时域描述，可称为点扩散函数;f(x，y)为清晰图像;*为时域卷积算子;n(x，y)为加性噪声。因此，式(1)表示为频域乘积，其频域表达式如下

在图像还原中，其最终目的就是为了能够得到一个无限接近原始图像的复原图像。在已知退化模型的前提下，对退化图像进行逆向推理，从而得到复原图像。目前，图像复原的方法较多，所熟知的有逆滤波复原法、基于Lucy－Richardson 算法、维纳滤波复原法和有约束最小平方复原法等，本文采用的是维纳滤波方法。

维纳滤波是一种为人们所熟知的线性图像复原法。在维纳滤波中，常会用到一种测试方法来测试图像复原得好坏

式中，e2值越小，表示图像复原的程度越高。

在式(3)中，f 是已知的原始图像，故只要求f^值最贴近f 即可，f^在频域的表达式为

式中

其中，H*(u，v)为复共轭函数;G(u，v)表示退化函数;Pn(u，v)表示噪声功率谱;Pf(u，v)表示原始图像的功率谱。但在实际操作中，Pn(u，v)和Pf(u，v)均无法精确计算，因此需要一个参数K 来替代，即式(4)改写为

从式中可得到运动模糊图像复原的关键在于H(u，v)与参数K 的计算，这两个参数计算值的精准度直接关系到模糊图像复原的好坏，其精度越高，则复原图像的效果越好［5］。

2 PSF 的确定

在匀速直线运动中，由于成像系统的曝光时间较短，设t，在不考虑翻转的情况下，物体以速度为v 沿与水平方向成θ 角进行相对运动，则点扩散函数h(x，y)与模糊尺度d=vt，可用式(7)表示

从式(7)中可以看出，若了解模糊角度θ 和模糊尺度d，便可得出h(x，y)。在通常情况下，将二维问题转化为一维问题。因此，就需要先求出模糊角度θ，然后再将模糊图像按照得出的模糊角度θ 进行逆向旋转。

2.1 模糊角度的确定

通常将原始图像视为自相关及其功率谱是各向同性的一阶马尔科夫过程，而运动模糊图像就是将其运动方向上的高频成分大幅降低，而相比其他方向对高频成分的降低作用要小得多，且在垂直于和模糊方向上的高频成分则无任何影响。因此，在鉴别模糊方向上，对模糊图像采用方向微分鉴别法，即对其进行方向性的高通滤波。在得到图像灰度值(绝对值)之后进行求和，当得到最小g(i，j)值后，其所对应的方向就是运动方向。陈前荣，李均利等人在方向微分上采用3×3 的微分算子［3－4］，其示意图如图2 所示。

图2 方向微分示意图

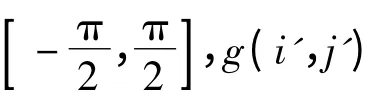
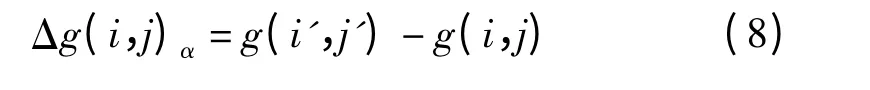
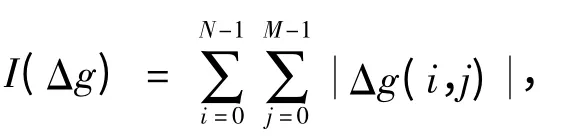
2.2 模糊尺度的确定

在得到模糊角度后，将图像按照模糊角度的逆方向旋转到水平方向，得到图像s(x，y)，对s(x，y)在水平方向上作一阶差分运算［6－7］，可得到s's(x，y);然后对s's(x，y)各行采用自相关运算，则第i 行的自相关函数的表达式为

在上式中，i，j 的取值范围分别为［1，M］，［－(N－1)，N－1］的整数。对c(i，j)各列求和可得到一条鉴别曲线。在这条曲线中，找出两个负峰值，则两点间的距离即为两倍模糊尺度［8］。在文中，运动模糊图像的模糊尺度选为20 pixel，其仿真结果如图3 所示。

图3 自相关模糊尺度鉴别

3 值自动估计

在用维纳滤波对模糊图像进行复原处理时的关键在于PSF 和K 的确定，在式(6)中的K 值，一般采用经验值或手工调节，该值固定。但在实际中K 值随图像局部变化而变化，其复原效果较差且实际操作步骤繁琐。本文采用一种自动估计［9］的方法，由于K 值是噪声功率谱与原图像功率谱的比值，因此只需找出K 值与E值所形成的波形图的最低点即可，其算法步骤如下:

(1)设置K0为初始参数，初始步长为ΔK，其中K0≪ΔK，设迭代步数为Km文中取ΔK=0.000 1，Km=100。

(2)进行循环迭代处理时，当循环到第m 次时，此时K 的计算方式为K=K0+mΔK，每循环一次可得到一个K 值，进行复原可得到一个E 值，最后可得到Km个E 值的序列。

(3)在这个序列中找出最小的E 值点，若该点不是第一或最后一个，则表示该点就是最佳估计点，对应的K 为最佳参数，则算法结束。

(4)若这个点是第一个点，则将步长减少10 倍，若是最后一个点，便将步长增大10 倍，再按照步骤(2)进行运算。

图4 K－E 关系图

4 实验结果及结论分析

文中以Lena 图像作为原始图像，并对其进行模糊处理且加入高斯噪声，模糊角度及模糊尺度分别为45°和20 pixel，噪声均值为0，方差为0.001 的高斯白噪声。运用文中的方法对其进行复原处理，其实验结果如图5 所示。

图5 运动模糊图像及维纳滤波复原结果

从上述各图可看出，在加入高斯白噪声的运动模糊图像采用一般的维纳滤波方法进行复原处理时，从主观上判断可知其结果并不理想，而从文中采用方法得到的复原图像可知，其复原效果更优。

5 结束语

对运动模糊图像的复原进行了研究，对运动模糊图像退化模型、维纳滤波对运动模糊图像复原的工作原理以及点扩散函数的求值过程进行了详细描述。在对模糊图像中点扩散函数处理时，运用了方向微分法、差分自相关法，在确定K 值时，并未采用传统的先验知识方法，而采用K 值自动估计法。同时，在运动模糊尺度和K 值自动估计的问题上做出了相应的改进。通过实验仿真表明，文中的方法对点扩散函数的确定有较好的效果，且通过仿真图可看出，相比于一般的维纳滤波复原方法，文中的方法综合运用对运动模糊图像的复原具有更好的效果。

［1］ 闫永存，杨燕翔，黄小莉，等.匀速直线运动模糊图像复原的改进算法［J］.电子设计工程，2012，20(3):145－148.

［2］ 王敏，田启川.改进的运动模糊图像复原算法［J］.微型机与应用，2011，30(6):31－40.

［3］ 陈前荣，陆启生，成礼智.基于方向微分的运动模糊方向鉴别［J］.中国图像图形学报，2005，10(5):590－595.

［4］ 李均利，储诚曦.方向微分分块统计的运动模糊方向鉴别［J］.中国图像图形学报，2013，18(7):776－782.

［5］ 金飞，张彬.基于维纳滤波的图像复原［J］.中国传媒大学学报，2011，18(4):19－23.

［6］ 郭红伟，付波，田益民，等.实拍运动模糊图像的退化参数估计与复原［J］.激光与红外，2013，43(5):559－564.

［7］ 陈前荣，陈启生，成礼智，等.运动模糊图像点扩散函数尺度鉴别［J］.计算机工程与应用，2004，26(1):41－45.

［8］ 郭永彩，郭瑞瑞，高潮.运动模糊图像点扩散函数的参数识别［J］.仪器仪表学报，2010，31(5):1052－1057.

［9］ 周玉，周序生，戴圣伟，等.一种改进的运动模糊图像复原算法［J］.计算机工程与应用，2009(10):49－52.