基于应变强度分布准则的边坡稳定性分析

陈正垚，李世海，冯 春

(1.石家庄铁道大学，河北石家庄 050043;2.中国科学院力学研究所，北京 100190)

0 引言

现有边坡稳定分析的理论与方法主要有以下几种［1］:一是工程地质分析法;二是极限平衡分析法;三是极限分析法;四是数值分析方法;五是可靠性分析方法。目前较为常见的是极限平衡法、极限分析法和有限单元法。极限平衡法［2］是当前岩土工程界广泛应用的方法，该方法基于刚塑性假设，且边坡滑动面被简化为圆弧形;对一般性边坡，由于地质分层以及材料参数的多样性，通过假定或简化模型进行分析计算，其结果是不理想的。有限元强度折减法［3-5］无需事先假定滑动面的形状和位置，只需对岩土体的强度参数不断的折减，使边坡岩土体因抗剪强度不能抵抗剪切应力而发生破坏，从而得到滑动面及其相应的安全系数。这使得有限元强度折减法与传统的极限平衡法相比具有很大的优势，之所以没有得到广泛的应用，究其根源，有限元计算的精度问题是重要的原因之一。影响有限元计算精度的因素有很多，比如，本构模型、岩土力学参数、网格的疏密、边坡失稳的评判准则、迭代次数等。

本构模型作为影响有限元计算精度的重要因素之一，一直是专家们研究的重要课题。吴顺川等［6］提出了遍布节理模型，认为岩体经强度折减后潜在破坏可能首先出现在岩体中或沿节理面或二者同时破坏，可同时考虑岩块和节理属性。钱建固等［7］在形分叉理论中引入非共轴弹塑性模型，构建了平面应变状态下的土体软化模型。杨光华等［8］基于Duncan-Chang非线性本构模型，提出在弹性阶段对弹性模量也进行折减的变模量弹塑性模型强度折减法。蓝航等［9］根据几何损伤理论中的裂隙张量和FLAC-3D莫尔-库仑模型的塑性流动格式建立考虑初始损伤的节理岩体弹塑性本构模型。姚仰平等［10］提出了土的统一硬化模型，该模型是基于剑桥模型，以变换应力方法和统一硬化参数为基本要素建立起来的弹塑性本构模型体系，它通过采用基于SMP准则、Lade准则或广义非线性强度理论的变换应力方法，实现了模型与强度准则的有机结合和模型的三维化。

本文基于有限元和离散元有机结合的计算软件CDEM［11-13］，通过引入能真实刻画岩土体渐进破坏过程的应变强度分布模型［14］，对均质边坡的稳定性进行了分析，提出了在数值分析中能体现历史沉积作用及土体应变硬化特征的土体强度随应力水平的增加而提高的强化公式。研究了主要参数对边坡稳定性、滑动面位置、裂缝发展范围以及破裂比的影响。总结得出了一种用破裂比评判边坡稳定性的新方法。

1 应变强度分布准则的基本原理

李世海、周东等［14］提出的应变强度分布模型，从细观层面上描述了岩土材料的损伤破裂机制。该模型假设岩土材料的破裂是其应变达到一定程度造成的，且材料中代表性体积单元的应变强度服从某种概率分布。以一个代表性体积单元为例，对单元施加剪切应变后，单元中低应变强度的部分被剪断，服从库伦摩擦定律，高应变强度的部分保持弹性，单元可以分为断裂及连续两个区域;随着剪切应变的增加，不同应变强度的部分依次发生断裂，单元的断裂域不断增大，当单元产生贯通的剪切面，即表明代表性体积单元已经完全剪断。

CDEM中可通过单元边界的断裂实现材料渐进破坏过程的模拟。因此，文章在CDEM的单元边界上引入上述应变强度分布模型式(1)、(2)。

其中，Fn、Fs为界面上的法向、切向弹簧力，α、β为拉伸、剪切完整度因子，Kn=EA/L、Ks=GA/L为界面上的法向、切向弹簧刚度，Δun(大于0表示拉伸位移，小于0表示压缩位移)、Δus为法向、切向弹簧位移，E、G为弹性模量及剪切模量，L为界面的特征厚度，A为界面的特征面积，φ为内摩擦角，F's=-KsΔ us为不考虑损伤情况下的切向弹簧力。

图1 应变强度分布准则的剪应力－剪应变曲线(出自引文［14］)Fig.1 Shear stress-strain curve corresponding to strain distribution criterion

拉伸、剪切完整度因子α、β与界面上特征拉伸应变ε、特征剪切应变γ之间存在函数关系，如式3、4。其中 ε = Δun/L，γ = Δus/L，εmin、γmin为出现拉伸、剪切损伤时的最小应变值，εmax、γmax为完整度因子为零(完全破坏)时的拉伸、剪切应变值。F(ε)、F(γ)为与应变相关的完整度概率，介于0与1之间。

F(ε)、F(γ)的概率分布可以选择不同的模式，如均匀分布、正态分布、韦伯分布等。以均匀分布为例，F(ε)、F(γ)可表述为5 式。

将理论公式给定具体参数得到如图1所示的剪应力-剪应变曲线。

应变强度分布准则的主控参数为内摩擦角φ和最大剪应变强度γmax以及最小剪应变强度γmin，该准则可以很好的表述材料的屈服和软化现象，当应变强度区间变化时可以得到脆断模型、软化模型以及理想弹塑性模型。在该准则下，细观的材料属性没有变化，只是不同状态下材料各部分作用方式发生变化，便可以得到复杂的宏观材料力学行为。

2 边坡稳定性分析

2.1 模型尺寸和边界条件

假定边坡沿纵向有足够的长度，认为是平面应变问题。采用Gmsh［15］进行建模和网格划分，采用基于有限元和离散元有机结合的计算软件CDEM进行数值计算，选用三角形平面应变单元建立边坡有限元模型，通过单元边界的断裂，实现边坡失稳破坏过程的模拟。模型的边界条件为，约束左侧和右侧边界的X方向位移，约束底部的X和Y方向的位移。主要研究的参数是内摩擦角φ和最大剪应变强度γmax以及最小剪应变强度 γmin。此处将 γmax和 γmin做关联处理，令 γ0=γmax=γmin×102，研究 φ 和 γ0对边坡稳定性的影响(图2，表1)。

图2 边坡模型尺寸Fig.2 Model size

表1 岩土和模型参数Table 1 Parameters of geotechnical and model

2.2 应变分布准则强化公式

第一阶段，令块体和界面都是线弹性模型，算至稳定。第二阶段将界面改为应变强度分布准则模型，继续算稳定。

计算的结果显示:第一阶段边坡内部会产生较大的应变，导致第二阶段计算一开始边坡内部较深部位就会有很多界面的应变超过γ0从而破坏，进而使内部产生大量的裂缝(图3)，这些裂缝逐渐发展，最终导致边坡失稳，且失稳时几乎所有的界面都破坏。

图3 边坡内部裂缝图Fig.3 Cracks of internal slope

运用这种方法，由于第一阶段计算产生的应变是随应力水平的增大而增大的，因此边坡深部的应变总是大于边坡表面的应变，在第二阶段应用应变强度分布准则计算时，总是深部先达到应变极限值γ0从而破坏，深部完全破坏后，裂缝才会向表面发展。这样显然是不合理的。

在这里，引入一种强化机制，假设随着应力水平的增大，土体的强度也会增大。其强化公式为:

对于具体的 γmax和 γmin，由于 γ0= γmax= γmin×102，所以6式可以写成:

运用该强化公式，第二阶段得到的边坡临界状态的裂缝发展情况(图4)。可以看到，在边坡失稳过程中，裂缝主要集中在滑动带附近。当滑动带中裂缝贯通并发展到一定程度后，边坡失稳破坏。

图4 边坡临界状态裂缝图Fig.4 Slope cracks of critical state

2.3 破裂比的定义

为了定量的研究边坡失稳过程中裂缝的发展情况，定义数值分析中破坏的界面数为破裂数d，破裂比，其中d1是当前阶段的破裂数，d2为标准的破裂数。在本节中取d2为模型总的界面数。对某一给定的工程边坡，当模型建成网格划分好后，可以通过软件统计出该模型总的界面数，即为标准破裂数。

2.4 内摩擦角对边坡失稳的影响

令γ0=210-3，研究φ对边坡失稳的影响。将边坡破坏时，位移超过坡高2%(本例中为0.2m)的部分标记出来，得边坡滑动范围图图5。可以得出，内摩擦角对滑动面的位置起主要控制作用，内摩擦角越大，滑动范围越小。统计不同内摩擦角时滑动的土方量，得出滑动方量与总土方量的比值——方量比，得到tanφ与方量比的关系曲线(图6)。图6说明方量比随着内摩擦角的增大而减小，当内摩擦角趋近于0时，方量比趋近于1，当内摩擦角很大时，方量比趋近于0。

统计不同内摩擦角时的破裂比，得到tanφ与破裂比的关系曲线(图7)。由图7可知，随着内摩擦角的增大，破裂数逐渐减少，破裂比逐渐减小。当内摩擦角趋近于0时，破裂比趋近于0.8，当内摩擦角很大时，破裂比趋近于0。并且在 φ～(5°～25°)时，tanφ与破裂比呈线性关系。

图6 tanφ与方量比关系曲线Fig.6 Curves of tanφ and square ratio

综上可知，内摩擦角主要控制滑动面位置，也即边坡的滑动范围。内摩擦角越小，边坡的滑动范围越大。

2.5 γ0对边坡失稳的影响

令φ=15°，研究γ0对边坡失稳的影响。将边坡失稳时，位移超过坡高2%(本例中为0.2m)的部分标记出来，得如下边坡滑动范围图(图8)并统计方量比(图9)。图8中，对于不同γ0滑动面的位置几乎不变，可以得出γ0对滑动面的位置影响很小，图9说明，γ0对边坡失稳时的滑动方量几乎没有影响。令φ=23°得出不同γ0对应的边坡失稳时的裂缝发展图(图10)。由图10得出γ0主要控制的是裂缝的发展程度，γ0值越小，裂缝发展程度越大。由图11(γ0与破裂比的关系曲线)可知，随着γ0的增大，边坡破裂比减小，两者关系大体呈线性。综上可知，在边坡失稳过程中γ0不影响滑动面位置，主要控制的是破裂比的大小也即裂缝的发展程度。

图7 tanφ与破裂比关系曲线Fig.7 Curves of tanφ and rupture ratio

图8 不同γ0时边坡滑动范围图Fig.8 Slope sliding range of different γ0

2.6 内摩擦角和γ0值对边坡稳定性和破裂比的影响

改变内摩擦角和γ0，得到边坡在不同tanφ值情况下对应的临界γ0值，从而得出对特定边坡由tanφ和γ0控制的边坡临界状态曲线(图12)。当已知某边坡的tanφ和γ0时，可以通过该曲线得知边坡是否稳定。位于曲线之上，边坡稳定;位于曲线之下，不稳定;在曲线上，则边坡处于临界状态。

下面通过改变内摩擦角和γ0值研究不同tanφγ0组合情况下，边坡的破裂情况。岩土参数同表1，通过数值分析得不同tanφ时，破裂比随γ0变化图(图13)，不同γ0时，破裂比随tanφ变化图(图14)。拟合得出tanφ-γ0-破裂比曲面图(图15)。

图9 γ0与方量比关系曲线Fig.9 Curves of γ0and square ratio

图10 不同γ0时边坡裂缝发展图Fig.10 Slope cracks of different γ0

图11 γ0与破裂比关系曲线Fig.11 Curves of γ0and rupture ratio

图12 边坡临界状态曲线Fig.12 Slope curve of critical state

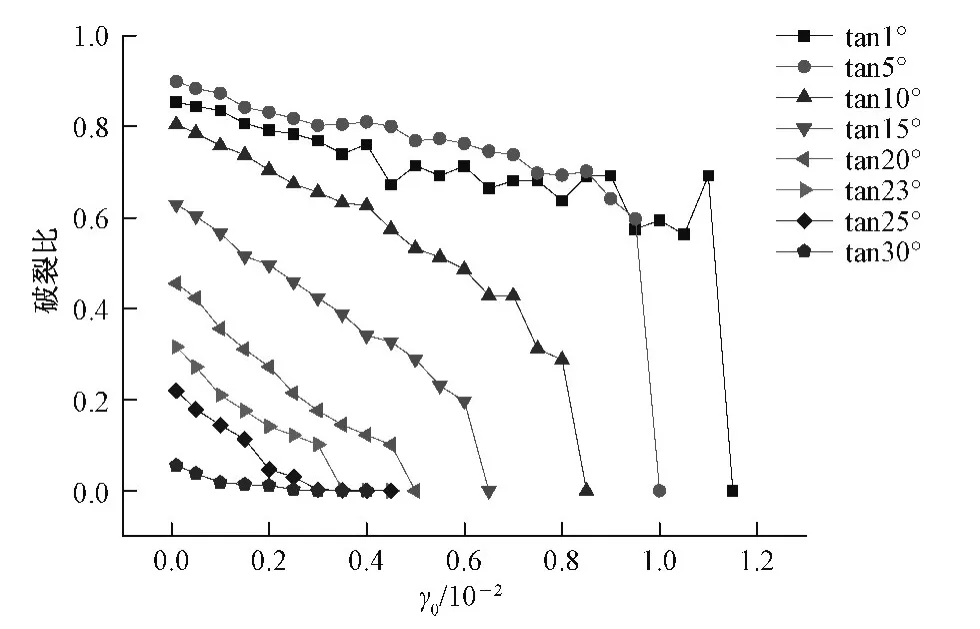
图13 不同tanφ时，破裂比随γ0变化图Fig.13 Curves of γ0and rupture ratio in different tanφ

图14 不同γ0时，破裂比随tanφ变化图Fig.14 Curves of tanφ and rupture ratio in different γ0

图13说明:对同一tanφ，破裂比随γ0的增大而减小，并且在临界值时，会有明显的突变，破裂比从较大的值突变到0。不同的tanφ决定了滑动范围的大小，也就决定了破裂比的最大值，tanφ值越小，破裂比的最大值越大。图14说明:对同一γ0值，破裂比随tanφ的增大而减小。对同一 tanφ，随着 γ0的增大，裂缝发展程度减小，其破裂比也减小。

图 15 tanφ-γ0-破裂比曲面图Fig.15 Surfaces of tanφ，γ0and damage ratio

3 运用破裂比评价边坡稳定性的可行性

在第二节中，研究了应变强度分布准则下，参数tanφ和γ0对边坡滑动范围、裂缝发展程度和破裂比的影响。据此提出以下评价边坡稳定性的方法。通过实地勘察，得到边坡的φ和γ0值的大体范围，以及地表裂缝的发展情况，对重要的坡体可通过钻孔了解坡体内部裂缝的发展情况。在勘察得到的φ和γ0值的范围内取值，进行数值分析，得出多组参数下，坡体裂缝的发展情况，与实地勘察得到的裂缝发展情况进行对比，找出比较接近的算例若干组。保持上述若干组中每组的φ值不变，折减γ0使坡体裂缝发展与实际最接近，此时的破裂数为当前破裂数d1，继续折减γ0使坡体失稳破坏，得到该滑动面所对应的最大破裂数d2。则破裂比(破裂比越接近1，表明边坡越靠近临界状态)。上述破裂比中的最大值，表征了坡体当前所处的最不利状态，根据该最不利状态下破裂比的具体数值，即可确定该边坡所处的稳定性级别。

该方法在坡体地质条件比较简单的情况下，得出的结果比较准确;当地质条件复杂，特别是坡体分层较多且层间岩土性质相差较大时，在用数值分析模拟坡体裂缝发展的阶段，不同层的参数有各自的取值范围，组合后工作量会增加很多，要得出裂缝发展情况与实际近似的算例，难度也会增加。对于大型坡体，其内部裂缝的发展情况无法全面的掌握，对于最后的结果也会有影响。

对于层理较多的坡体，可以主要研究薄弱层，其他的层取具有代表性的几组参数。对大型坡体，可以重点勘探主要的裂缝，辅以坡体表面的裂缝与数值结果进行对比分析。

4 结论

本文基于有限元和离散元有机结合的计算软件CDEM，通过引入能真实刻画岩土体渐进破坏过程的应变强度分布模型，对均质边坡的稳定性进行了分析。在数值分析中，针对自然界中土体的应变硬化效应引入一种土体强度随应力水平的增加而提高的强化机制，从而较好地模拟了边坡失稳过程中，裂缝的发生和发展过程。

研究了内摩擦角和γ0对边坡稳定性的影响，得出了可以判断特定边坡稳定性的边坡临界状态曲线。通过单因素研究，得出内摩擦角对滑动面的位置起主要控制作用，内摩擦角越大，滑动范围越小。γ0对裂缝的发展起主要控制作用，γ0值越小，裂缝发展程度越大。得出了tanφ-γ0-破裂比曲面图。

提出了运用破裂比评价边坡稳定性的方法，该方法通过边坡表面及内部的裂缝信息反演获得应变强度分布准则需要的参数(内摩擦角、应变强度等)，进而通过分析不同潜在滑动模式下的破裂比给出边坡所处的最不利状态，最后根据最不利状态下边坡破裂比的具体数值给出边坡的稳定性级别。

［1］杨天鸿，张锋春，于庆磊，等.露天矿高陡边坡稳定性研究现状及发展趋势［J］.岩土力学，2011，32(5):1437-1472.YANG Tianhong，ZHANG Fengcun，YU Qinglei，et al.Research situation of open-pit mining high and steep slope stability and its developing trend［J］.Rock and Soil Mechanic，2011，32(5):1437-1472.

［2］张发明，陈祖煜，弥宏亮.三维极限平衡理论及其在块体稳定分析中的应用［J］.水文地质工程地质，2002，4:33-35.ZHANG Faming，CHEN Zuyu，MI Hongliang.3-D limit equilibrium theory and its application in block stability analysis［J］.Hydrogeology and Engineering Geology，2002，4:33-35.

［3］李红卫，马惠民，张忠平.强度折减法在高含水滑坡稳定性分析中的应用［J］.中国地质灾害与防治学报，2009，20(3):27-30.LI Hongwei，MA Huimin，ZHANG Zhongping.Application of strength reduction method in stability analysis of a landslide with high water content［J］.The Chinese Journal of Geological Hazard and Control，2009，20(3):27-30.

［4］陈昌富，翁敬良.基于广义Hoek-Brown准则边坡稳定性分析强度折减法［J］.中国地质灾害与防治学报，2010，21(1):13-18.CHEN Changfu，WENG Jingliang.Strength reduction method based on generalized Hoek-Brown criterion for slope stability analysis［J］.The Chinese Journal of Geological Hazard and Control，2010，21(1):13-18.

［5］候连成，王笑二，王家伟，等.基于强度折减法的某变电所边坡稳定性分析［J］.水文地质工程地质，2012，39(1):72-74.HOU Liancheng，WANG Xiaoer，WANG Jiawei，et al.Slope stability analysisby strength reduction fora substation［J］.Hydrogeology and Engineering Geology，2012，39(1):72-74.

［6］吴顺川，金爱兵，高永涛.基于遍布节理模型的边坡稳定性强度折减法分析［J］.岩土力学，2006，27(4):537-542.WU Shunchuan，JIN Aibing，GAO Yongtao.Slope stability analysis by strength reduction method based on ubiquitous-joint model［J］.Rock and Soil Mechanic，2006，27(4):537-542.

［7］钱建固，吕玺琳，黄茂松.平面应变状态下土体的软化特性与本构模拟［J］.岩土力学，2009，30(3):617-622.QIAN Jiangu，LV Xilin，HUANG Maosong.Softening characteristics of soils and constitutive modelingunder plane strain condition［J］.Rock and Soil Mechanic，2009，30(3):617-622.

［8］杨光华，张玉成，张有祥.变模量弹塑性强度折减法及其在边坡稳定分析中的应用［J］.岩石力学与工程学报，2009，28(7):1506-1512.YANG Guanghua，ZHANG Yucheng，ZHANG Youxiang.Variable modulus elastoplastic strength reduction method and its application to slope stability analysis［J］.Chinese Journal of Rock Mechanics and Engineering，2009，28(7):1506-1512.

［9］蓝航，姚建国，张华兴，等.基于 FLAC-3D的节理岩体采动损伤本构模型的开发及应用［J］.岩石力学与工程学报，2008，27(3):572-579.LAN Hang，YAO Jianguo，ZHANG Huaxing， et al.Development and application of constitutive model of jointed rock mass damage due to mining based on FLAC3D［J］.Chinese Journal of Rock Mechanics and Engineering，2008，27(3):572-579.

［10］姚仰平，侯伟，罗汀.土的统一硬化模型［J］.岩石力学与工程学报，2009，28(10):2135-2151.YAO Yangping，HOU wei，LUO ting.Unified hardening model foe soils［J］.Chinese Journal of Rock Mechanics and Engineering，2009，28(10):2135-2151.

［11］LI Shihai，ZHAO Manhong，WANG Yuannian，et al.A new numerical method for dem-block and particle model［J］.International Journal of Rock Mechanics and Mining Sciences，2004，41(3):436-436.

［12］Wei Zuoan，Li Shihai，J.G.Wang，et al.A dynamic comprehensive method for landslide control［J］.Engineering Geology，2006，84(1-2):1-11.

［13］Continuum-based Discrete ElementMethod and its Application.Li Shihai 2008.9，Beijing DEM’08.

［14］LI Shihai，ZHOU Dong.Progressive failure constitutive model of fracture plane in geomaterial based on strain strength distribution［J］.International Journal of Solids and Structures，2013，50:570-577.

［15］C.Geuzaine，J.-F.Remacle.A three-dimensional finite elementmesh generatorwith built-in pre-and postprocessing facilities［J］.International Journal for Numerical Methods in Engineering，2009，79(11):1309-1331.