泥石流巨石冲击下的钢构格栅坝动力响应分析

王秀丽，胡志明，崔晓燕

(1.兰州理工大学土木工程学院，甘肃兰州 730050;2.西部土木工程防灾减灾教育部工程研究中心，甘肃兰州 730050;3.兰州石化职业技术学院，甘肃兰州 730060)

0 引言

泥石流是山区常见的一种自然灾害，往往具有暴发突然、破坏性大的特点，成为大多数山地国家和地区造成经济损失和人员伤亡的灾害之一，因而受到众多国家的关注和重视［1］。我国备受泥石流灾害困扰，其中，舟曲8·8特大泥石流灾害共造成4496户、20227人受灾，共有1501人遇难，264人失踪，直接经济损失超过10×108元，是建国以来我国最严重的泥石流灾害事件。

目前，国内外关于泥石流拦挡坝的研究应用多侧重于重力实体坝，王秀丽等对普通实体坝加以改进，提出了新型泥石流拦挡结构，并对其进行研究对比［2］。然而实体坝对泥石流冲积物的拦截并无选择性，无形中加重了坝体负担。且泥石流对建筑物的冲击破坏主要由泥石流中巨石的冲击造成。钢构格栅坝具有“拦排皆备”的优点，可以有效的拦截泥石流中的巨石，减轻泥石流对建筑物的冲击破坏。国内外关于钢构格栅坝的研究只局限于其拦砂性能，拦石效果，腐蚀性以及对生态环境的影响［3-5］，而对钢格栅坝受泥石流巨石冲击作用下的动力响应并无相关分析。

为了有效抵抗泥石流巨石的冲击作用，确保钢构格栅坝在巨石冲击下仍能继续承载，发挥拦石作用，本文利用国际通用计算动力荷载的非线性有限元软件ANSYS/LS-DYNA进行数值模拟。用钢球冲击坝体模型来模拟泥石流中巨石对钢格栅的冲击作用，得到不同冲击位置下结构的动力响应，为钢构格栅坝结构性能的进一步研究奠定了基础。

1 冲击作用分析

1.1 巨石冲击脉冲形式

对于钢格栅坝而言，由文献4知，b/dmax≤1.5时(b为柱子之间的纯间隔，dmax为石块最大粒径)，能够非常有效地拦蓄泥石流巨石。本文模型中b=0.4m，则dmax≥0.267m，故对本格栅坝模型而言，将 d≥0.267m的石块定义为泥石流巨石，拦截效果最佳。

冲击荷载是指外荷载随时间迅速变化的荷载，是一种短时作用。国内学者陈洪凯、刘雷激等根据实测的泥石流冲击力过程曲线对泥石流冲击荷载进行了研究，将泥石流冲击荷载概化为锯齿形脉冲、矩形脉冲和尖峰型脉冲三类［6-7］。

钢格栅坝只对泥石流中巨石进行拦挡，以受巨石的冲击作用为主，属尖峰型脉冲(图1)。该类波形反映泥石流冲击作用时间短，全过程仅几毫秒到几十毫秒，认为是泥石流体中粒径较大的固相颗粒或块石动力作用的结果，能更精确的反应钢构格栅坝受泥石流巨石的冲击。

图1 冲击荷载Fig.1 Impact load

1.2 巨石冲击力计算方法

泥石流对钢格栅坝的冲击力包括泥石流整体冲击力和泥石流中巨石的冲击力［8］，由于格栅坝受力面积小，作用于坝体的整体冲击力将很小，主要以巨石的冲击力为主。

式中:Fb——泥石流巨石冲击力(kPa);

E——工程构件弹性模量(kPa);

J——工程构件截面中心轴的惯性矩(m4);

V——石块运动速度(m/s);

W——石块重量(kN);

g——重力加速度(取g=9.8(m/s2);

L——构件长度(m);

α——块石运动方向与构件受力面的夹角(°)。

1.3 钢球模拟巨石冲击

本文采用直径为0.3m的钢球模拟泥石流冲击过程中的巨石，在有限元软件ANSYS/LS-DYNA中建立钢球模型。钢球选取ANSYS/LS-DYNA中提供的刚体单元SOLID168单元，其本构关系采用刚体模型。钢球网格尺寸取为0.02m，其有限元模型网格划分如图2所示。

图2 钢球有限元模型Fig.2 The finite element model of steel ball

由邓虎、陈宁生等对三眼峪泥石流的动力特性参数的分析可知，通过对舟曲三眼峪沟泥石流堆积区巨石的实地测量，得到沟口堆积扇区堆积的最大颗粒直径为7.5 m，从而计算得出泥石流中巨石流速为10.95 m/s［9］。模拟中取钢球的初速度为 10 m/s。

1.4 钢球模拟巨石冲击结果

由式(1)，巨石对结构的冲击力与工程构件弹性模量、截面中心轴的惯性矩等拦挡结构的性能有关，且与石块的运动速度、重量等冲击物本身的特性有关。巨石对拦挡坝的冲击力随着冲击能量的增大而增大，筑坝体材料刚度越大冲击力也越大［10］。

LS-DYNA模拟过程中，将同样大小的钢球以相同的初速度作用于格栅坝中间榀顶层梁柱节点和中间榀顶层柱中部(图3)。本文中定义钢球作用于格栅坝中间榀顶层梁柱节点为冲击工况一，将钢球作用于格栅坝中间榀顶层柱中部定义为冲击工况二。冲击力模拟结果如图4所示。

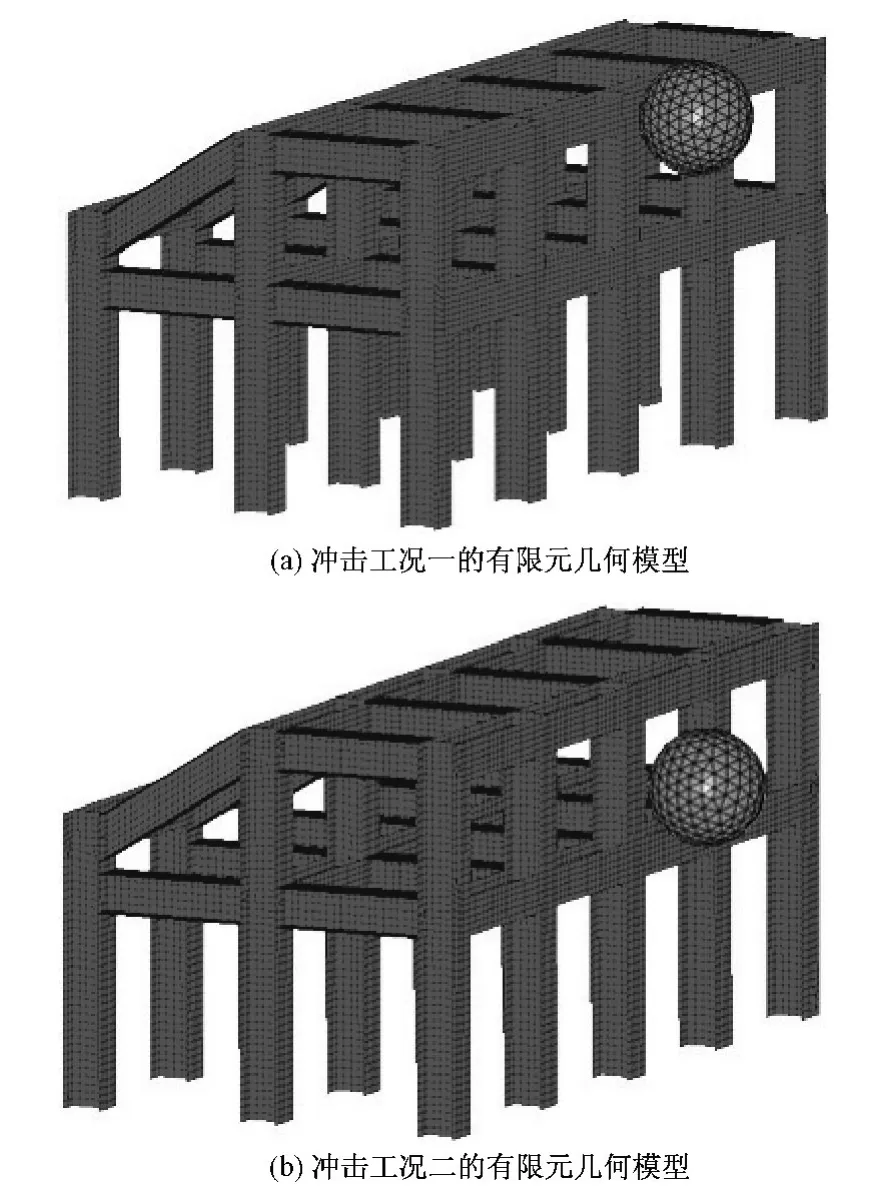
图3 有限元几何模型Fig.3 The finite element geometry model

结果显示钢格栅坝不同冲击位置的最大冲击力截然不同，且冲击力时程差别较大(图4)。冲击工况一作用下钢球最大冲击力为481.37kN，且冲击力随着作用时间逐渐削弱;冲击工况二作用下钢球最大冲击力为261.36kN，且冲击力会在作用后期增大，之后再减弱。

图4 冲击力时程Fig.4 The schedule of Impact

模拟过程中两种冲击工况只是冲击结构时冲击位置做了改变。冲击工况一位于格栅坝中间榀顶层梁柱节点处，结构传递冲击力性能较好且刚度较大;冲击工况二直接作用于格栅坝中间榀顶层柱中部，构件刚度较小。由以上分析可知钢球模拟泥石流巨石冲击钢格栅坝时，冲击力的大小与被冲击构件的刚度有关，构件刚度越大，冲击力越大，反之刚度越小，冲击力越小;且构件越刚冲击力时程曲线越接近于图1的尖峰型脉冲图形，构件较柔时，冲击力峰值不明显，且在冲击后期冲击力大小将出现回弹。

2 钢构格栅坝有限元分析

2.1 建立模型

2.1.1 单元类型

钢格栅坝有限元模型中，构件选用4节点空间薄壳单元SHELL163单元，单元厚度8mm，剪切因子取5/6。SHELL163单元共有12种算法供选择，本文采用程序默认的Belytschko(def)算法。

2.1.2 材料属性

本模型材料屈服强度 235MPa，弹性模量205GPa，泊松比0.3，密度 7.85 ×103kg/m3，本构关系采用双线性各向同性模型，材料的屈服遵循 Von Mises屈服准则。

2.1.3 网格划分

本文钢格栅坝由五榀钢架通过横梁及水平梁相连，各榀间距0.5m，每榀钢架为两跨两层，跨度均为0.5m，第一层高度0.61m，第二层高度0.4m。模型中钢构件均采用H100X100X8X8工字型钢，网格划分尺寸为20mm。钢构格栅坝的有限元网格划分如图3所示。

2.1.4 接触定义

本模型选择ANSYS/LS-DYNA程序提供的单面自动接触算法ASTS(Automatic Surface To Surface)。

2.1.5 边界条件

钢格栅坝柱脚采用外包式刚接柱脚，本模型边界条件采用全自由度固定约束。

2.2 有限元结果分析

2.2.1 Von Mises应力

钢格栅坝属对称结构，可给出一半结构的应力云图，在两种冲击工况作用下的应力云图如图5及图6所示。

由图5及图6可知，冲击作用点周围的应力会首先增大并达到屈服应力值，被冲击榀上构件的应力值最大，与被冲击榀相邻的结构各榀应力较大，各边榀构件应力相对较小;且梁柱节点处单元应力值比梁、柱构件中部应力值大，符合结构在冲击作用下的受力特征。两种工况下结构在支座处及冲击作用点处应力最大，且都已达到屈服强度。

对本结构按图7所示各控制点提取单元应力值(表1)。由表1可知，1、3、5点位于梁端处，其应力逐次增大;2、4点处于梁跨中，应力相对较小，且4点处的应力较2点处的大。5、7、9点处的应力均达到屈服强度，6点的应力小于8点处的应力值(冲击作用于6点处除外)。3、10、12点处3点较10点大，均大于12点处的应力值;同样的7、10两点处应力要大于11点处的值，且7点距作用点较近，应力大于10点处应力值。分析比较可知梁柱两端应力值与跨中应力值相比，明显较大;且节点处或跨中控制点距冲击作用位置越远，应力值越小。通过对两种冲击工况下结构各单元应力值的对比分析可知，除被冲击部位以外，冲击工况一作用下结构的应力值高于工况二的应力值。工况一作用下结构传力较为均匀，冲击作用传至结构支座处，使支座处钢柱均达到屈服，整体结构可能丧失承载能力;而工况二作用下结构在被冲击部位周围应力很大，构件已达到屈服，结构其他部位的应力值相对较小，结构在被冲击榀上破坏严重，其他部位仍可继续承载。

图5 工况一Von Mises应力云图Fig.5 Von Mises stress nephogram under the working condition one

表1 单元应力值Table 1 Unit stress value

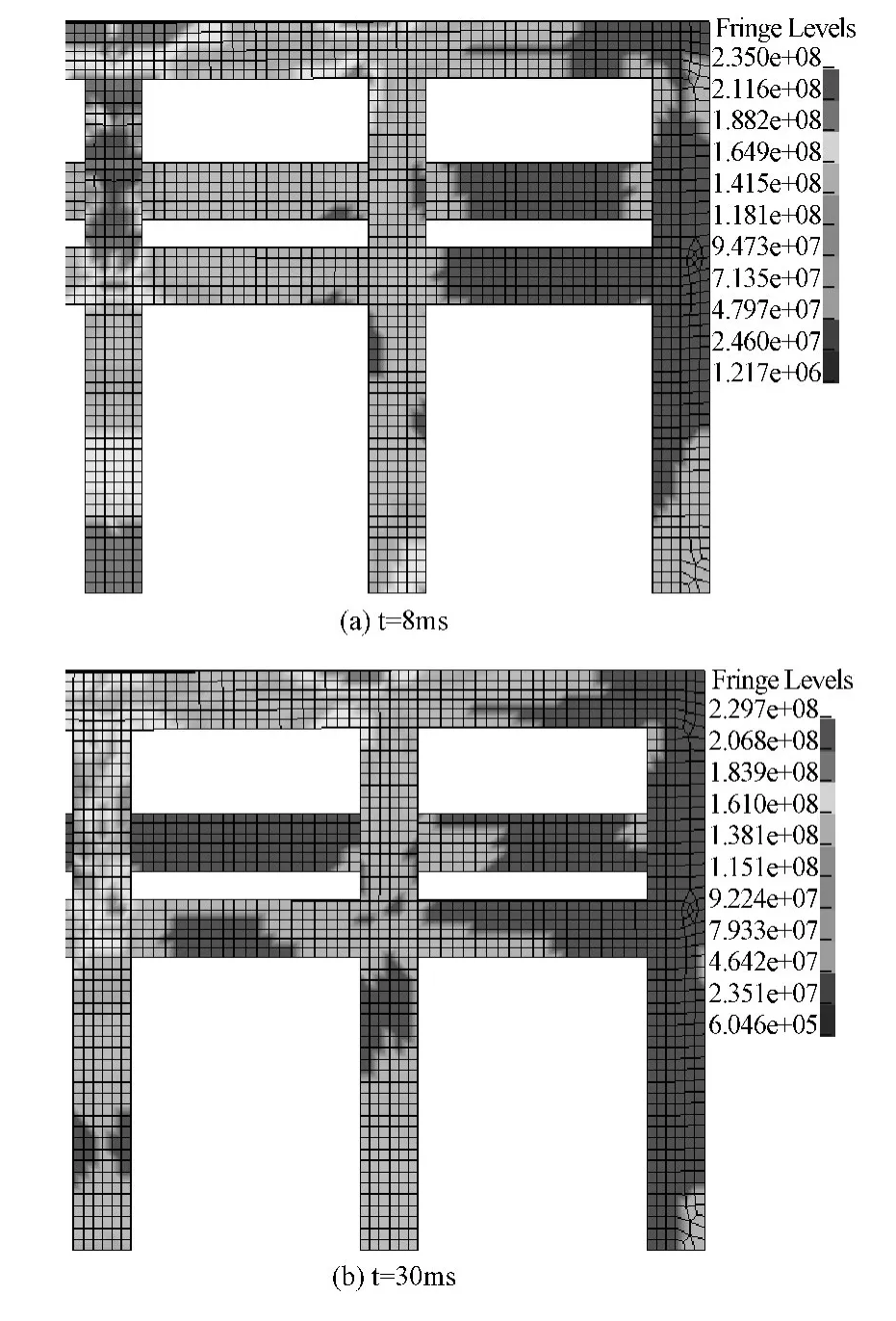
图6 工况二Von Mises应力云图Fig.6 Von Mises stress nephogram under the working condition two

图7 控制点布置图Fig.7 Arrangement of control points

2.2.2 位移

冲击作用下结构变形如图8所示。

图8 钢格栅坝变形图Fig.8 Deformation figure of steel grille dam

由于本结构模型属于对称结构，故只对格栅坝的一半进行取点并提取位移值，各控制点位置如图7所示，位移值见表2。

表2 各点最大位移值Table 2 Maximal displacement of each point

由各点位移值可知，在冲击荷载作用点周围结构构件的位移值最大，离冲击点距离越远构件位移越小，即构件位移在冲击点周围由近到远逐渐减小，且位移变化以冲击点为圆心呈辐射状。

通过对两种冲击工况下结构各点位移值的对比，由表2数据可知，冲击工况二下结构各点(冲击作用点除外)的位移明显小于工况一作用下的位移值。究其原因，由图3知，在工况二的冲击作用下，钢球冲击力明显小于工况一下的冲击力，故使得结构位移值较小;且在冲击工况二作用下，被冲击柱构件发生较大变形，其作为结构耗能段将冲击作用的能量消耗，致使结构整体的位移响应较小。比较图9及图10中1～9号控制点各点的位移时程，在冲击工况一作用下结构各点均产生了不可恢复的塑性变形，且距冲击作用点越近，塑性变形越大，冲击作用点处的塑形变形值将近6mm;冲击工况二作用下结构只在冲击点处产生塑性变形，可达到22mm，结构其他部位的构件仍处于弹性工作阶段，且位移值很小，只有2mm左右。

图9 工况一作用下各控制点位移时程Fig.9 Displacement schedule of all measuring points under the working condition one

图10 工况二作用下各控制点位移时程Fig.10 Displacement schedule of all measuring points under the working condition two

3 结论

本文就钢构格栅坝结构模型，利用非线性有限元软件ANSYS/LS-DYNA，用钢球模拟巨石对结构进行数值模拟。通过对冲击荷载作用下钢构格栅坝的全过程动力响应分析，得到以下结论:

(1)作用在结构上的冲击力大小与被冲击构件刚度大小密切相关，被冲击构件刚度越大，结构受到的冲击力越大，反之，冲击力越小;且构件刚性越强，冲击力时越接近理想时程曲线。

(2)钢构格栅坝在冲击作用下，冲击作用部位、结构支座部位及梁柱节点部位响应较大，破坏最严重，设计时应予以加强。冲击作用榀及与冲击作用榀相邻各榀的上述部位单元应力达到钢材的屈服强度，且比较之下冲击作用部位构件位移值最大，两种工况下位移峰值分别达到了14.5mm及25.4mm。

(3)钢构格栅坝不同位置遭受冲击作用时结构响应完全不同，与冲击力作用在梁柱节点时相比较，冲击力作用在构件中部时结构整体响应明显较小。冲击工况一时结构各点位移值约为工况二下位移值的2倍，且工况二下结构单元应力值明显减小。

［1］陈继华，王秋军，张彦林.泥石流防治研究［J］.科技广场，2011(2):20-22.CHEN Jihua，WANG Qiujun，ZHANG Yanlin.Debris flow prevention and control research［J］.Science and Technology Square，2011(2):20-22.

［2］王秀丽，黄兆升.冲击荷载下泥石流拦挡坝动力响应分析［J］.中国地质灾害与防治学报，2013，24(4):61-65.WANG Xiuli，HUANG Zhaosheng.Dynamic response analysis of the new debris flow block under impact load［J］.The Chinese Journal of Geological Hazard and Control，2013，24(4):61-65.

［3］懒户俊彦，葛西俊一郎，山口健太郎，等.采用格栅型钢结构过水大坝防止泥石流［J］.水土保持科技情报，2000(2):37-39.LANHU Junyan， GEXI Junyilang， SHANKOU Jiantailang，et al.Using grid steel structure in water dam to prevent mudslides［J］.Soil and Water Conservation Science and Technology Information，2000(2):37-39.

［4］中村.钢制格栅坝的性能设计［J］.水土保持科技情报，2001(5):14-16.ZHONG Cun.The performance of steel grille dam design［J］. Soil and Water Conservation Science and Technology Information，2001(5):14-16.

［5］李铁军，李晓华.日本有关透过型坝拦截泥石流的调查分析［J］.水土保持科技情报，2002(5):25-26.LI Tiejun，LI Xiaohua.Investigation and analysis of Japanese grille dam block debris flow［J］.Soil and Water Conservation Science and Technology Information，2002(5):25-26.

［6］陈洪凯，唐红梅，陈野鹰，等.公路泥石流力学［M］.北京:科学出版社，2007.CHEN Hongkai，TANG Hongmei，CHEN Yeying，et al.Highway debris flow force［M］.Beijing:Science press，2007.

［7］刘雷激，魏华.泥石流冲击力研究［J］.四川联合大学学报，1997，1(2):99-102.LIU Leiji，WEI Hua.Debris flow impact study［J］.Journal of Sichuan United University，1997，1(2):99-102.

［8］DZ/T0239-2004，泥石流灾害防治工程设计 规范［S］.北京:中国标准出版社，2010.DZ/T0239-2004，Debris flow disaster prevention and control of engineering design specifications［S］.Beijing:China Standard Publishing House，2010.

［9］邓虎，陈宁生，胡桂胜，等.甘肃舟曲三眼峪沟泥石流动力学特征参数计算［J］.重庆交通大学学报(自然科学版)，2011，30(4):833-838.DENG Hu，CHEN Ningsheng，HU Guisheng，et al.Dynamics characteristic parameters in third valley gully，Zhouqu county， Gansu province ［J］. Journalof Chongqing Jiaotong University(Natural Science Edition)，2011，30(4):833-838.

［10］何思明，吴永，沈均.泥石流大块石冲击力的简化计算［J］.自然灾害学报，2009，18(5):51-56.HE Siming，WU Yong，SHEN Jun.Simplified calculation of impact force of big stones in debris flow［J］.Journal of Natural Disasters，2009，18(5):51-56.