基于Monte Carlo法的滑坡稳定可靠性分析研究——以玉树西航电站H1滑坡为例

侯小强

（甘肃建筑职业技术学院，甘肃兰州 730050）

0 引言

滑坡的稳定性往往受到许多不确定性因素的影响，如岩土体结构的不均匀性、地震荷载、降雨等，强度参数受勘察和试验的人为因素，导致试验数据一定程度的离散，这样给滑坡稳定性准确评价带来了一系列困难[1-4]。目前，采用一些传统的计算方法，利用极限平衡原理对条块进行静力分析，求解抗滑力（矩）R和滑动力（矩）S，并将其比值F=R／S定义为安全系数，作为边坡稳定的评价指标，或者根据岩土性质和特征，建立有限元模型进行数值模拟并计算出安全系数。这些方法尽管已被工程界和学界所广泛采用，然而以安全系数作为滑坡稳定性的评价指标，是根据岩土参数的平均值进行求解，产生定值结论，忽视了岩土性参数离散性的影响，因而它的大小并不能完全表征滑坡的安全程度，就会出现分析是安全的但却发生滑坡[5-10]。鉴于此,要保证滑坡安全可靠，应引入可靠度理论和方法，将这些不确定性因素，如容重、内摩擦角及粘聚力等参数的离散性，利用Monte-Carlo法则，根据输入的参数及设定的要求，由随机函数随机生成服从变量分布规律的一系列参数组，重复计算n次，从而计算出失稳概率和安全系数进行定量的可靠性评价。

1 Monte Carlo法基本原理

蒙特卡洛（Monte Carlo）模拟是一种通过设定随机过程，反复生成时间序列，计算参数估计量和统计量，进而研究其分布特征的方法。蒙特卡洛模拟方法的原理是当问题或对象本身具有概率特征时，根据抽样计算统计量或者参数的值；随着模拟次数的增多，可以通过对各次统计量或参数的估计值求平均的方法得到稳定结论。

Monte Carlo法给出的解按大量的检测统计都达到了平均值，因此，该解中包含了平均值附近的浮动量，而且不可能达到100%的置信度。要计算Monte Carlo算法的统计偏差，就必须采用与统计变量相关的各种统计方法。

设对于一般的边坡稳定性问题,根据岩土体结构、破坏机理和受力状况,可以建立如下的状态函数:

式中：X1,X2,……Xn分别为容重、粘聚力、摩擦系数等随机变量,它们具有一定的分布(大多服从正态分布或对数正态分布),其统计值为己知。

设状态函数为安全系数,且随机地从各个随机变量Xi(i=,12,……,m)的母体中抽取一个具有相同分布变量,由式（3）、式（4）求得一个安全系数的随机样本K'。如此重复，直至达到预期精度的充分次数N，就可得到N个相对独立安全系数样本值K1，K2，.....,KN,安全系数所表征的极限状态为K=1。构造随机变量为：

设在N次试验中,出现Wi=1(i=1,2.....,N)，即K≤1的次数为M,则滑坡的破坏概率为:

当N足够大时，由安全系数的统计样本值K1，K2，.....KN可以较精确地拟合安全系数的概率分布F(k)，并估计其分布参数。其均值和标准差分别为：

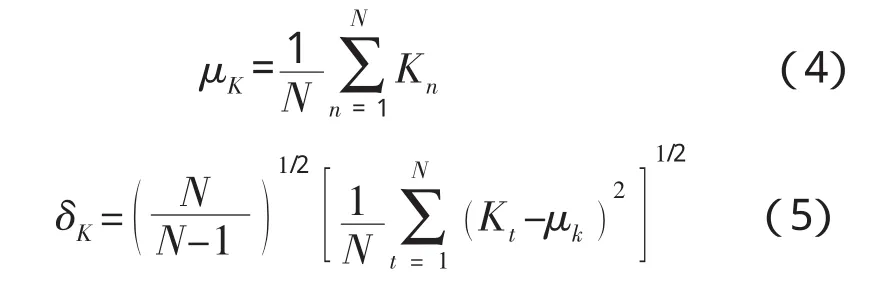
由计算边坡概率，可得到滑坡可靠性指标为：

破坏概率为：

2 案例分析

以玉树县结古镇应急燃油电站H1滑坡为例。

2.1 滑坡地形地貌

H1滑坡地貌类型为构造侵蚀中低山，地势总体西高东低，南高北低，坡高近200m，坡度40°～55°，坡向79°。滑坡后缘高程为3 910.20 m，前缘高程为3 719.7 m，相对高差为190.5 m，前缘原地貌较平缓，现为人工挖掘陡坎，近似南北向展布，坎高5～15 m。滑坡纵剖面形态为折线型，坡度较陡，整体上为上陡下缓,如图1所示。

图1 H1滑坡平面布置示意图

2.2 滑坡空间形态及规模

H1滑坡平面形态近似“舌”形，纵剖面形态为折线型，坡度较陡，整体坡度40°～55°，整体呈上陡下缓，滑坡分布高程3 719.7～3 910.2 m，轴线水平投影长265 m，斜长636 m，滑体厚度7.2～19.0 m，平均厚度15.4m，前缘宽175m，中、后缘宽80～140m，面积 3.89×104m2，体积 70.07×104m3，为中型土质滑坡。滑动方向约79°，前缘为不规则弧形，滑坡后壁高39.7 m，近于直立，呈圈椅状，冲沟发育，如图2所示。

2.3 滑体物质组成及结构特征

图2 H1滑坡模型和量危险滑弧条分图

根据Monte-Carlo法计算要求，保证取样的代表性，采取多钻孔，取样位置在滑体各个部位，详见图1和图2。本次共采用8个钻孔，12个探孔，取样36个，其中探孔深度一般在3～5 m，分别取样1个，钻孔深度达22～25 m不等。该钻孔基本穿过滑带，进入滑床，在滑床以上取样总数达24个，每个钻孔分上中下三处位置取样。根据钻探孔取样分析，滑坡区滑体主要由坡残积碎石土组成，滑体厚度7.2～19.0 m，以碎石土褐黄色、青灰色，稍湿，稍密～中密，最大粒径180 mm，一般粒径20～40mm，其中粒径大于20 mm者约占55%～65%,2～20 mm者约占20%～35%，余为土质及少量砂质，碎石磨圆度差，多呈棱角～次棱角状，主要成分为灰岩，分选性差。根据取样试验数据分析，Monte-Carlo法计算要求，分别计算平均值、标准差、最大值和最小值。天然状态下，容重16.12～18.28 kN/m3，标准差0.216，平均值17.20 kN/m3；粘聚力10.20～30.20 MPa，标准差 2.8，平均值 16.2 MPa；内摩擦角6.15°～37.75°,标准差 2.8，平均值 21.95°。降雨状况下，容重 18.45～19.55 kN/m3，标准差 0.10，平均值19.1 kN/m3；粘聚力 8.10～22.3 MPa，标准差 1.65，平均值 14.0 MPa；内摩擦角 7.92°～29.52°,标准差2.16，平均值 18.72°，如表 1。

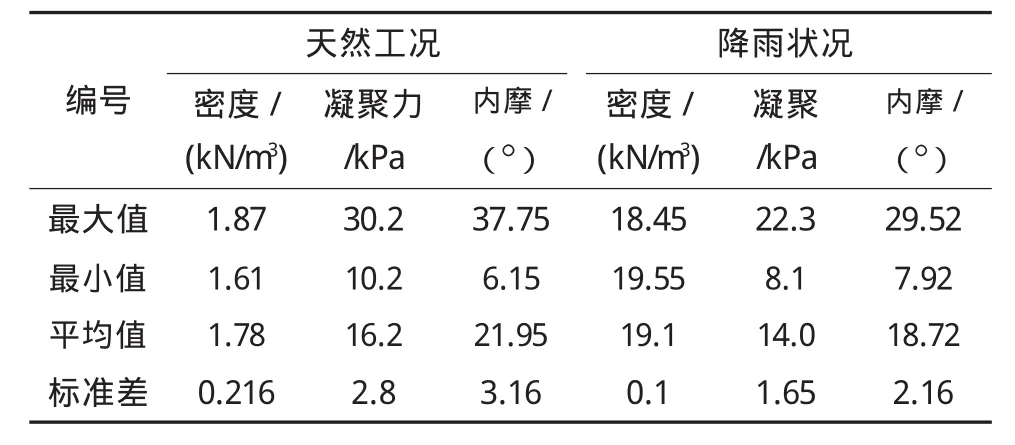
表1 计算采用岩土参数统计表

2.4 计算数据分析

由于该滑坡滑坡岩土组成的复杂性，试验数据存在一定程度离散性，符合正态分布规律，如图3～图6所示。选择主滑方向剖面，利用实测剖面，通过CAD中DXF导入计算软件SLOPE/W中，建立合理的计算模型进行分析，计算次数从500次、1 000次、3 000次、5 000次、7 500次、10 000次分别进行计算，计算结果如表2。

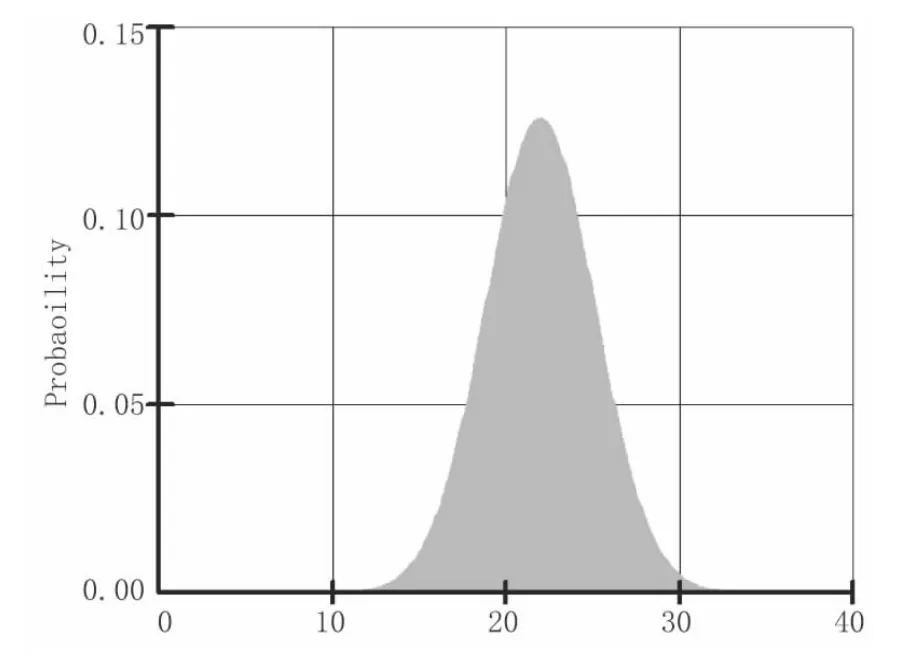
图3 天然状态下内摩擦角FOS概率分布

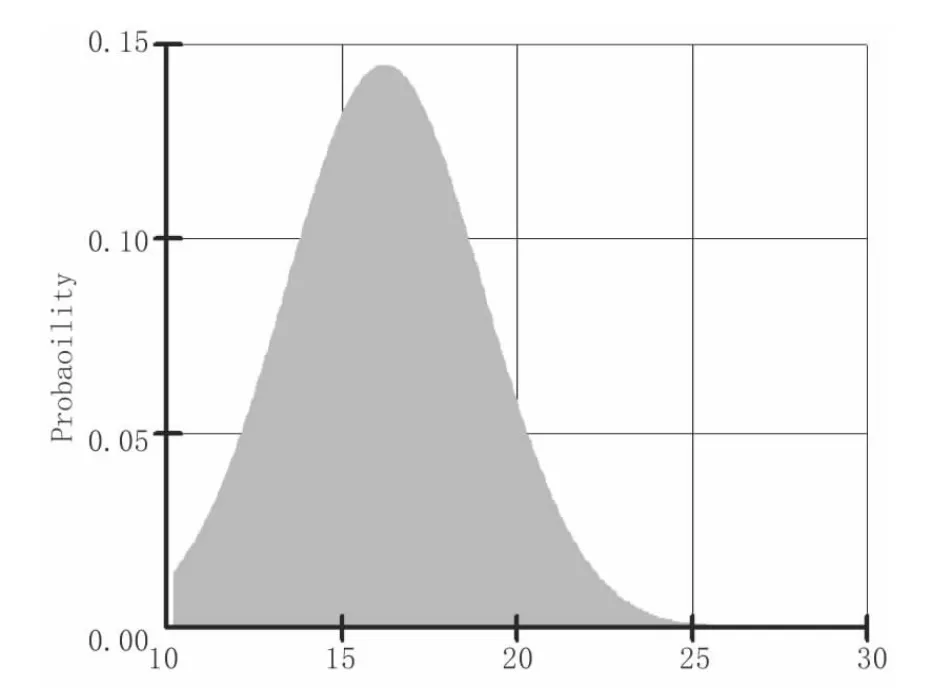
图4 天然状态下粘聚力FOS概率分布

图5 降雨状态下内摩擦角FOS概率分布

图6 降雨状态下粘聚力FOS概率分布

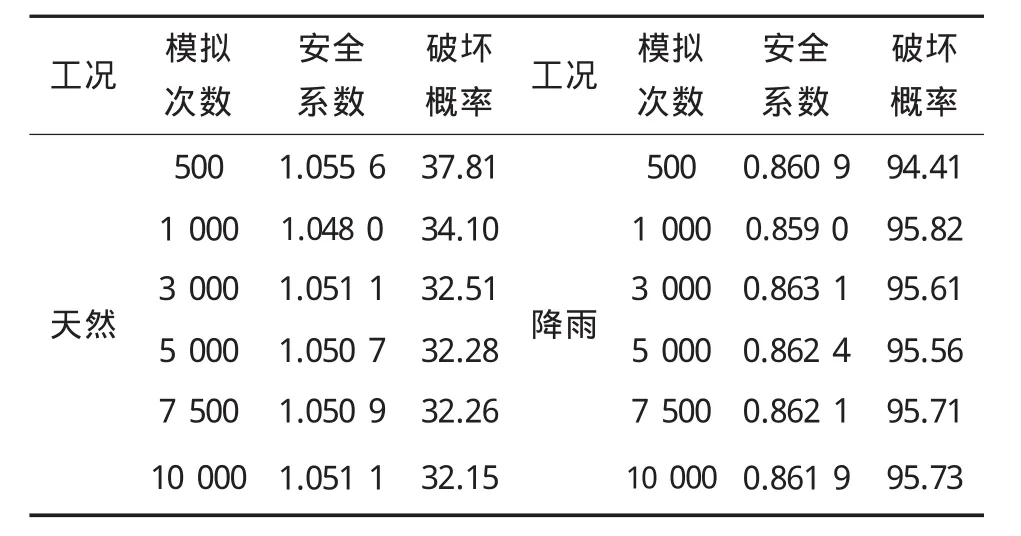
表2 两种工况下可靠性指标计算表

对玉树西航电站H1滑坡进行分析，从图7～图10可以得出，在两种工况下安全系数、破坏率数据，在模拟500～3 000次之间波动稍大，在3 000～10 000次之间，随着模拟次数增加，安全系数、破坏率趋于稳定，说明在模拟3 000次以上基本稳定。

图7 天然安全系数

图8 降雨安全系数

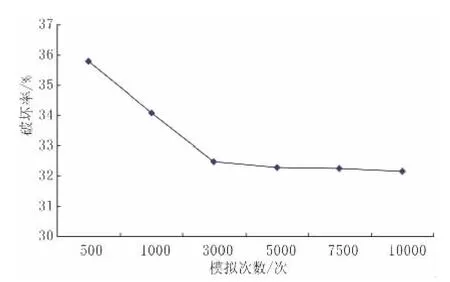
图9 天然状态下破坏率

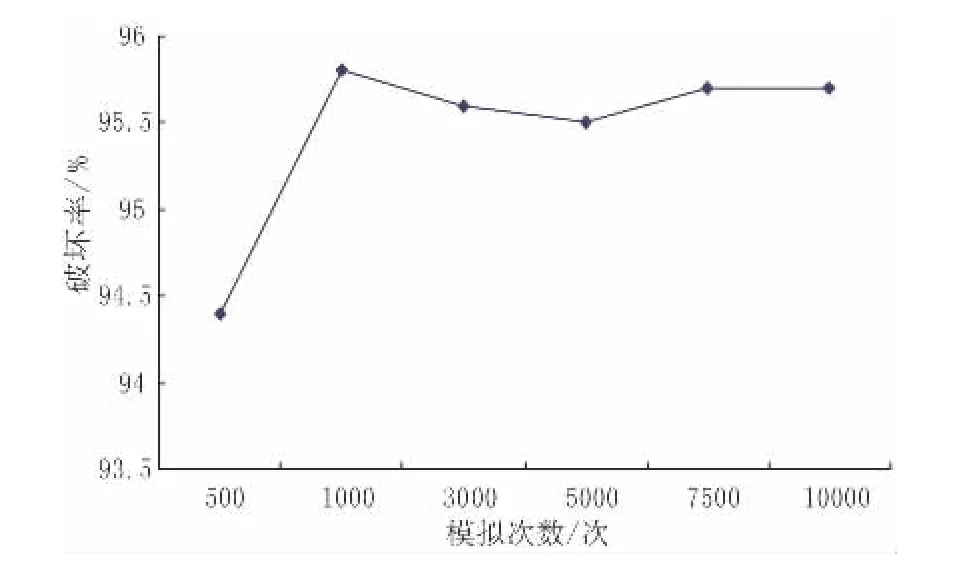
图10 降雨状态下破坏率

在天然状态下H1滑坡安全系数基本在1.05附近属于基本稳定，破坏率在32.15%～37.8%之间，在降雨状况下H1滑坡安全系数基本在0.863附近属于不稳定，破坏率在96.6%～95.7%之间。根据徐卫亚[11]对于边坡稳定性等级划分标准，如表3所示,天然工况下该滑坡属于中等危险，稳定等级属于3级，在降雨工况下该滑坡属于必然破坏，稳定等级属于1级。这说明天然状态下,H1滑坡基本稳定，在降雨工况下，必然失稳,对滑坡进行治理非常必要。

表3 边坡稳定性等级

3 结语

（1）传统稳定系数虽以数值表示安全度的指标，但并不是定量地表示安全性程度。采用Monte-Carlo法则，特别适合滑坡岩土的离散性，可以将内摩擦角φ、凝聚力c参数在离散范围内，每次可以采用新的随机变量进行滑坡的安全计算，从安全系数和破坏概率分析结果相结合作为可靠性判断指标。

（2）采用Monte-Carlo法则，玉树县结古镇应急燃油电站H1滑坡为例，在天然和降雨两种工况下，随着模拟次数增加，各项指标逐渐趋于稳定，由此说明，在滑坡稳定性分析时建议模拟3 000次以上各项指标更稳定。

（3）采用Monte-Carlo法则进行滑坡稳定性分析评价，能反映出滑坡的安全程度，确定稳定定级，可为滑坡治理是否必要提供更加可靠的依据。

[1]徐青，陈士军，陈胜宏.滑坡稳定性分析与安全系数取值研究[J].中国地质灾害与防治学报，2006，17(3)：58-62．

[2]赵寿刚，兰雁，沈细中，等.蒙特卡罗法在土质边坡可靠性分析中的应用[J].人民黄河，2006，28(5)：65-66，73．

[3]侯小强，田树涛.基于MIDAS/GTS高边坡开挖及加固施工稳定性分析[J],路基工程，2013，（6）：178-181.

[4]常亮，李萍，陶福平，等.黄土强度指标对边坡稳定性的影响研究[J].公路交通科技，2008，28(3)：20-24．

[5]李扬，杨继红，刘汉东.岩体结构控制下的边坡稳定性多因素敏感性分析[J].铁道建筑，201l(1)：88-90．

[6]郭长宝，张永双，陈情来，等．基于瑞典条分法数值解的边坡蒙特卡罗可靠性分析[J].水文地质工程地质，2007(4)：18-21．

[7]聂士诚.土质边坡稳定的可靠度分析及其土性参数的敏感性研究[D].长沙：中南大学，2003．

[8]罗文强，黄润秋，张倬元.斜坡稳定性概率分析的理论与应用[M]．武汉：中国地质大学出版社，2003．

[9]李萍，王秉纲，李同录，等.陕西地区黄土路堑高边坡可靠度研究[J].中国公路学报，2009，22(6)：18-25．

[10]徐,青，陈士军，陈胜宏．滑坡稳定分析剩余推力法的改进研究[J].岩土力学，2005，26(3)：465-470．

[11]徐卫亚.滑坡失稳破坏概率及可靠度研究[J].灾害学，1995，10(4)：33-37.