干旱半干旱区森林蓄积量高光谱遥感估测技术1)
2014-03-05王靖吴见
王 靖 吴 见
(滁州学院,滁州,239000)
森林是重要的自然资源,森林蓄积量标志着林业的经济效益,准确地估测森林蓄积量能够为森林规划和经营提供科学依据[1-2]。随着3S 技术的发展,利用遥感结合地面实测数据对森林蓄积量进行估测,成为了目前林业关注的焦点[3]。多数研究主要利用蓄积量和遥感光谱信息之间的相关关系来估测森林蓄积量[4-5],这类方法有线性、幂函数和对数等各种形式,而且自变量也不相同。多数学者根据植被的反射光谱特征,用原始波段及其派生波段、红光与近红外波段的反射率或其他因子及其组合所获得的植被指数(Ⅰ)与蓄积量的关系来估算森林蓄积量。但该方法的估测精度不高,使用范围局限性大,很难满足实际需求[6]。神经网络包含许多功能简单的神经元[7-8],能够自主学习,通过学习算法寻找网络最优的阈值和权值[9],具有计算速率高、精确逼近复杂非线性函数功能[10]。采用神经网络结合遥感数据进行森林蓄积量估测的研究正处于探索阶段[11-12]。另外,有一些研究采用了k-近邻法对森林蓄积量进行估测,取得了较好的效果[13]。
大多研究仅使用一种或者两种技术定量估测研究区的森林蓄积量,无法在同一研究区域系统地比较现有不同方法的优劣,难以确定研究区最优的蓄积量估测技术。为了对干旱半干旱区森林蓄积量估测方法进行系统地比较分析,本文以北京怀柔为研究区域,利用高光谱卫星影像数据比较了目前常用的几种蓄积量定量估测技术,旨在为更深入地研究干旱半干旱区森林蓄积量估测方法提供参考。
1 研究区概况
怀柔县位于北京市的东北部,是燕山山脉、内蒙古高原、华北平原的过渡地带,具有2 128.7 km2的土地面积。该区地形有平原、浅山、深山3 种类型,且南部为草原,北部环山.宜林山场森林面积41%,山地面积占88.7%。怀柔县海拔在34 ~1 661 m 之间,地势整体上为北高南低。该区气候春秋季节干旱多风且短暂,夏天温热湿润,受海洋气团影响大,冬天寒冷干燥,受西伯利亚冷空气影响较大。常年降水量470~850 mm,年平均气温在9 ℃。土壤类型主要包括风砂土、棕壤、褐土、草垫土等。
2 研究方法
2.1 数据获取及预处理
选取2001年5月19日北京怀柔部分地区的EO-1 Hyperion 高光谱数据。Hyperion 数据空间分辨率为30 m,光谱分辨率为10 nm,共有242 波段,其中可见光近红外波段(VNIR)为1 ~70 波段,短波红外波段(SWIR)为71~242 波段。
首先删除44 个未定标、20 个受水汽影响严重、2 个重复的波段,然后对剩余的176 个波段进行smile 效应去除、条纹去除、坏线修复等处理,最后检验处理后的影像,再删除7 个低质量波段。对剩余169 个波段(被删除的具体波段为:1 ~7;58 ~78;121~129;166~180;185~186;224~242),采用FLAASH软件进行大气纠正,获取反射率影像,进而以1 ∶50 000 地形图对大气纠正后的影像进行几何纠正,纠正平均误差为0.35 个像元。
在1 ∶50 000 地形图上,以2 km×2 km 进行系统样地点布设,设置30 m×30 m 的样地657 个,其中:落入森林中的样地有179 个,实际调查样地160 个,有19 个样地因自然条件限制无法调查。样地调查内容为优势树种、平均胸径、平均树高、冠幅、枝下高、坡向、坡度、样地中心点以及4 个顶角坐标等,采用平均标准木法测定标准地森林蓄积量,调查时间在2001年5—6月。
2.2 高光谱特征参数选取及相关性
2.2.1 高光谱特征参数选取
很多学者分析了高光谱遥感的特点,认为许多宽波段影像无法识别的对象信息能够被高光谱数据识别,且选取部分敏感波段要比选取全部波段的效果好。光谱微分技术一方面可以提取波长位置、宽度、深度等吸收峰参数,另一方面可以减弱辐射、散射、大气吸收等影响,以降低系统误差。采用前人研究的一阶微分法对高光谱数据进行处理:ρ'(λi)=[ρ(λi+1)-ρ(λi-1)]/2Δλ。式中:ρ'(λi)代表λi处一阶微分值;Δλ 代表λi与λi+1间的距离;ρ(λi+1)、ρ(λi-1)分别代表i+1 和i-1 波段的反射率;λi代表i波段的波长。
通过森林蓄积量与影像反射率相关性分析,在波长656、802、925 nm 处相关系数具有最大值(-0.671、0.745、0.762);通过森林蓄积量与一阶微分光谱相关性分析,在442、596、684 nm 处相关系数具有最大值(-0.757、-0.694、-0.723)。选取了森林蓄积量,与原始反射率、一阶微分光谱相关性较大的10 个波段或波段组合参数,另外参考前人研究成果[14],又选取了19 个参数,详细信息见表1。
2.2.2 蓄积量与高光谱参数相关性
随机选取30 块样地,分析森林蓄积量与29 个特征参数的相关关系(见表2)。从表2可以看出,光谱面积参数中仅SDb未达显著水平;植被指数参数中,除了Ⅰ3、Ⅰ4、Ⅰ5未达到极显著差异外,其他参数都达 到了极显著差异,其中Ⅰ10、Ⅰ7、Ⅰ2的相关系数达0.7 以上;光谱位置参数中,F925、D442、F802、D684的相关系数绝对值达0.7 以上。选取相关系数达到极显著差异水平的Ⅰ1、Ⅰ2、Ⅰ6、Ⅰ7、Ⅰ8、Ⅰ9、Ⅰ10、SDy、SDr、Rg、Rr、Dy、Dr、F656、F802、F925、D442、D596、D684等19 个参数对森林蓄积量进行估测。

表1 森林蓄积量高光谱估测模型特征参数的定义
2.3 森林蓄积量定量估测方法
2.3.1 主成分回归(PCR)和偏最小二乘回归(PLSR)法
PLSR 与PCR 方法的原理非常类似,PCR 首先把自变量信息进行分解,得到特征向量和得分矩阵,从而实现与因变量结合,构建回归估测模型。而PLSR 在对自变量信息进行分解的同时,也将因变量信息融入了进来,计算得到的不同因子的相关性,从高到底对各因子相关性进行排序,得到的矩阵权重体现了自变量信息和因变量的协方差结构。PLSR 的步骤[15]为:
1)将自变量矩阵X=(xij)n×p 和因变量矩阵Y=(yij)n×m 分别分解为特征向量:
X=TP+E;
Y=UQ+F。
式中:P(d×p 阶)与Q(d×m 阶)各代表X 与Y 的载荷阵,E(n×p 阶)与F(n×m 阶)各代表X 与Y 的残差阵,T、U 各代表X、Y 的特征因子矩阵(n×d 阶,d表示抽象组分数)。
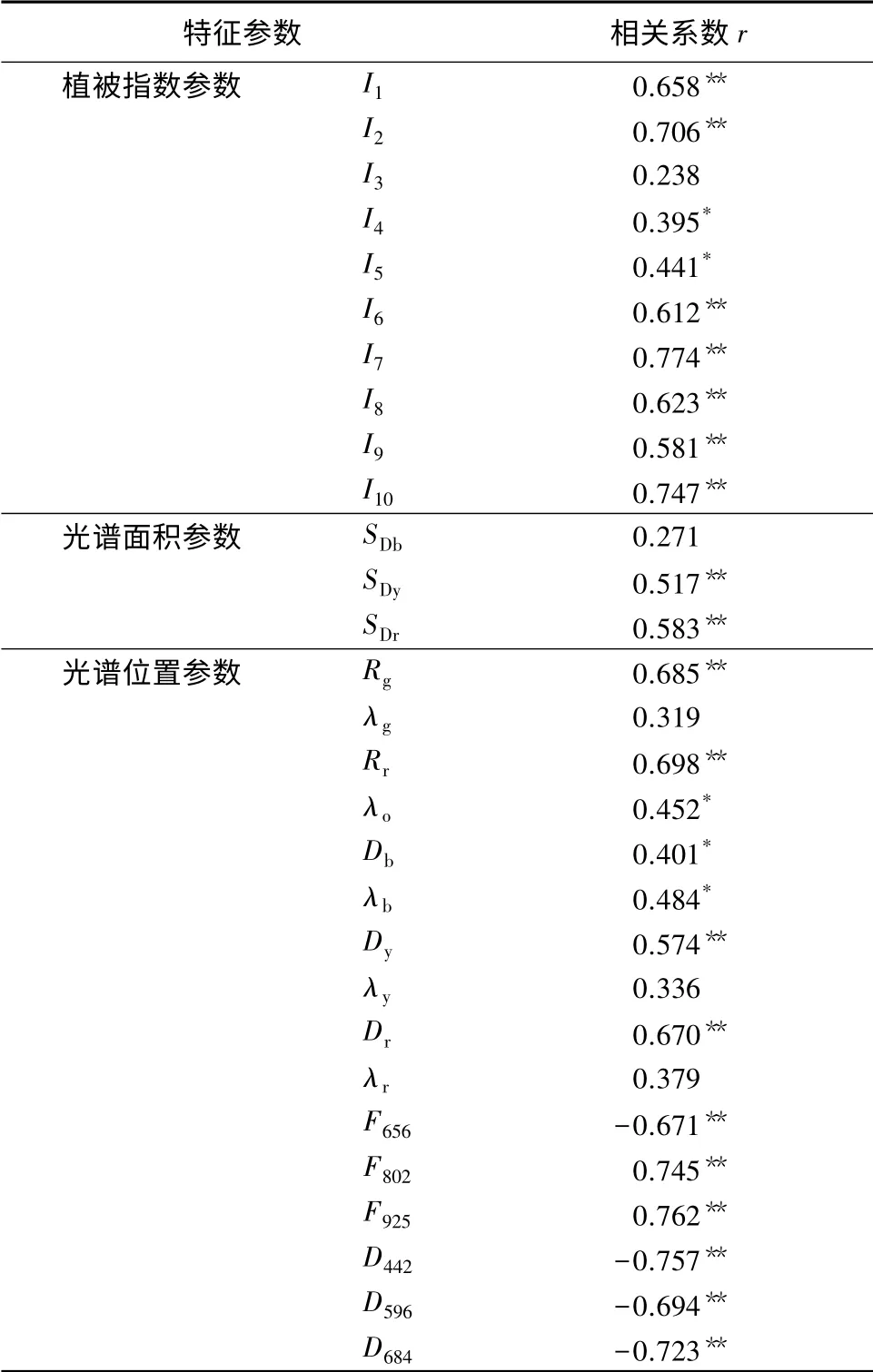
表2 高光谱估测模型特征参数与森林蓄积量的相关系数
2)将Y 和X 依据特征向量的相关性完成分解,进而建立回归模型:
U=TB+Ed。
式中:B 代表的是d 维对角回归系数阵,Ed代表的是随机误差阵,并且以交叉验证法来计算最佳维数d,最佳维数d 是最小均方根误差对应的维数。
以选取的19 个参数分别进行PLSR 与PCR 模型构建,其中验证样本80 个,建模样本80 个,根据均方根误差相关系数指标R2和相对误差对建模和验证结果进行检验。式中:yi是实测值,是预测值,n是样本数,RMSE越小说明预测效果越好,取P 的绝对值均值作为评价标准,值越小说明预测效果越好,R2取值0 ~1 之间,值越大说明预测效果越好。其中,对于参与建模变量个数的确定,首先允许被选取的全部变量进行建模,从第一个变量建模开始,计算出建模精度,当第二个变量加入时,如果建模精度提高,则继续加入第三个变量,以此类推,直至精度开始下降,则不再加入新的变量,此过程考虑因子之间的多重共线性,综合决定最后用于回归模型构建的自变量。
2.3.2 BP 和RBF 神经网络法
BP 神经网络具有输层、隐藏和输出三层,属于前向多层网络。当输入学习样本,激活函数通过输入、中间层传播至输出层,并从输出层向隐藏层根据实际误差修正连接权值,最终回归输入层。经过误差反向传播修正,网络得到的正确率随之上升。在网络连接值得到调整后,能够对新的样本进行非线性映像。BP 网络的学习速率一般为0.01 ~0.10,过低训练时间长,过高学习过程不稳定。该网络对神经元个数比较敏感,个数多不仅增加训练时间,而且会把噪声等混入,导致泛化能力下降,个数少会达不到训练精度要求。
RBF 具有对非线性函数全局最优和最佳逼近的优点,在输入和隐藏层之间具有非线性变化的性能,该网络一方面计算量小,另一方面泛化能力强。与BP 神经网络相比,RBF 网络加快了计算速度且避免了陷入局部极值。
假设将k 维向量X'={X'1,X'2,…,X'k}作为RBF 网络的输入层数据,D={D1,D2,…,Dl}作为隐含层的L 维向量,其一维输出向量f(X')为:
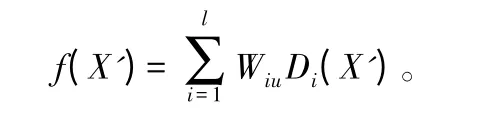
式 中:i是节点数,i=1,2,…,l;u是输出神经元数,u=1,2,…,h;Wiu是第i 个隐藏层单元至输出单元的权值,公式为:

Di(X')是隐藏层的径向基函数,公式为:
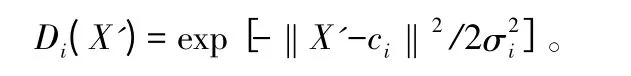
式中:‖X'-ci‖是欧式范数,ci是隐藏层节点中心,采用K-均值聚类法计算获取,σi是宽度或方程,可调节网络灵敏度,计算公式为
训练样本选取80 个,验证样本选取80 个,通过反复测试,确定神经元个数,BP 网络22 个,RBF 网络为40 个。
2.3.3 k-近邻法
k-近邻法是指根据与未知样本最近的k 个点来判断未知样本属于哪种类别。假设全部实例都是多维空间里面的点,采用标准欧式距离定义一个实例的最近邻,设:<a1p,a2p,…,arp,…,anp>为p 的特征向量,其中arp 为一个实例的第r 个属性值,则pi和pj两个实例的距离d(pi,pj)可表达为:
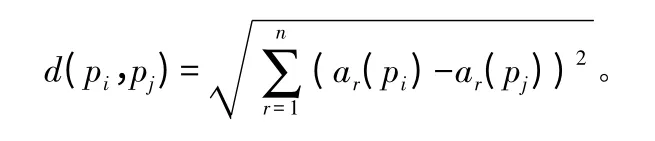
一般情况其中n 代表特征矢量的个数,若距离未知样本Si较近的样本点少,则该样本覆盖区域大,反之则小。该方法受噪声影响,特别是空间中的孤立点的影响较大,原因在于k 个最近邻样本点的作用是一样的。由于实际情况是近距离的样本作用较大,故采用距离加权法计算不同距离样本点的贡献,公式为:
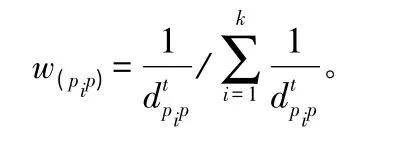
式中:t 值为2;pi为训练样本点;p 为待预测点,i=1,2,…,k;wpip为p 和pi的距离权重;d(pip)为p 和pi的距离。则点p 的蓄积量计算公式为:
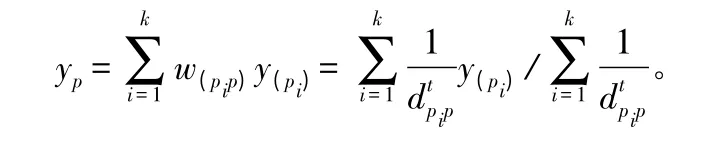
式中:y(pi)代表点pi的蓄积量,yp代表点p 的蓄积量。
3 结果与分析
3.1 主成分回归(PCR)和偏最小二乘回归(PLSR)法
3.1.1 PCR 模型估测蓄积量
从表3可以看出,仅采用植被指数参数作为变量估测蓄积量时,参与建模变量个数为3,R2为0.689,Rmse为12.54,P 为13.62%,Rmse为13.02;仅采用光谱面积和位置参数时,参与建模变量个数达7个,建模精度较高,R2为0.827,Rmse为9.37,但验证精度降低较大,P 为15.11%,Rmse为16.84,可见该参数模型不稳定,参与建模变量过多,导致过度拟合现象严重;当采用植被指数、光谱面积和位置参数同时估测蓄积量时,参与建模变量5 个,其验证精度最好,P 为12.97%,Rmse为12.70。PCR 模型估测蓄积量结果见图1。

表3 PCR 模型建模与验证结果
3.1.2 PLSR 模型估测蓄积量
从表4可以看出,仅采用植被指数参数作为变量估测蓄积量时,参与建模变量个数为4,R2为0.7 4 9,Rmse为1 1.5 6,验证P 为1 2.8 5%,Rmse为12.38,与PCR 相比,建模和验证效果均有所提高;仅采用光谱面积和位置参数时,参与建模变量个数达6 个,建模和验证精度均较低,由此反映出此类参数对森林蓄积量的估测效果较植被指数差;当采用植被指数、光谱面积和位置参数同时估测蓄积量时,参与建模变量6 个,建模R2为0.801,Rmse为10.16,P 为11.26%,Rmse为11.37,与PCR 相比,效果较好(见图2)。

表4 PLSR 模型建模与验证结果

图1 PCR 模型估测蓄积量结果

图2 PLSR 模型估测蓄积量结果
3.2 BP 和RBF 神经网络法
3.2.1 BP 神经网络模型估测蓄积量
从表5可以看出,仅采用植被指数参数作为变量估测蓄积量时,训练步长为55,时间为5 s,与其他参数变量相比,训练步长最大,时间最短,且验证效果最好,P 达10.06%,Rmse为11.06;仅采用光谱面积和位置参数作为变量估测蓄积量时,效果最差;当采用植被指数、光谱面积和位置参数同时估测蓄积量时,效果比仅采用光谱面积和位置参数好,但比仅采用植被指数参数差。分析原因可能是由于光谱面积和位置参数代入BP 网络训练时,对蓄积量的估测效果不理想,影响了整体估测结果。BP 模型估测蓄积量结果(见图3)。
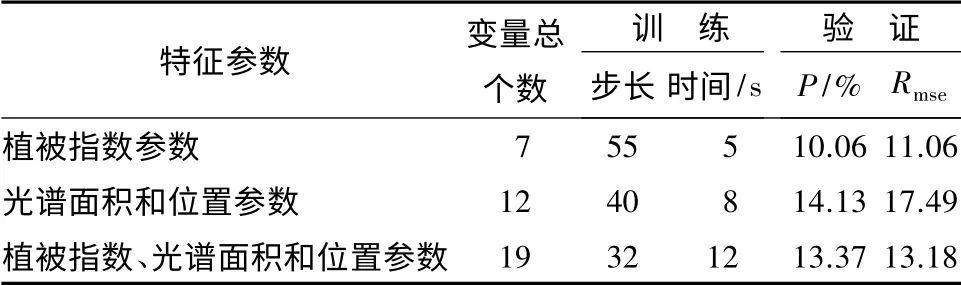
表5 BP 神经网络模型训练与验证结果

图3 BP 模型估测蓄积量结果
3.2.2 RBF 神经网络模型估测蓄积量
从表6可以看出,仅采用植被指数参数作为变量估测蓄积量时,训练步长为39,时间为10 s,P 为11.03%,Rmse为11.84,其效果比仅采用光谱面积和位置参数好,但比采用植被指数、光谱面积和位置参数同时作为输入参数效果差,但采用19 个变量同时作为输入参数时,训练步长为28,时间13 秒,P 为9.87%,Rmse为10.09,与BP 网络相比,验证精度稍有提高。RBF 模型估测蓄积量结果(见图4)。

表6 RBF 神经网络模型训练与验证结果

图4 RBF 模型估测蓄积量结果
3.3 k-近邻法
从图5可以看出,k 值从1 增大到8 时,Rmse不断降低,随后又有上升趋势,但总体变化不大,当k=8 时,Rmse的值最小,达9.38,P 值为8.56%。k-近邻法估测蓄积量结果(见图6)。
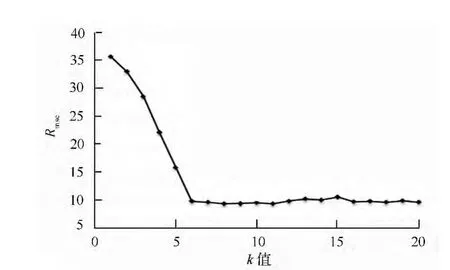
图5 不同k 值下的Rmse

图6 k-近邻法估测蓄积量结果(m3/hm2)
从上文对各方法的结果分析中可以看出,与本文其他方法相比,k-近邻法对森林蓄积量的估测效果最佳,以植被指数、光谱面积和位置参数同时作为输入参数的RBF 神经网络模型估测蓄积量的效果次之。
4 结论与讨论
以北京怀柔为例,对当前流行的多种高光谱遥感森林蓄积量估测技术进行了对比分析,得到如下结论:
1)与森林蓄积量达到极显著差异水平的Ⅰ1、Ⅰ2、Ⅰ6、Ⅰ7、Ⅰ8、Ⅰ9、Ⅰ10、SDy、SDr、Rg、Rr、Dy、Dr、F656、F802、F925、D442、D596、D684等19 个参数对森林蓄积量进行估测。
2)PCR 和PLSR 估测森林蓄积量时,采用植被指数、光谱面积和位置参数同时估测蓄积量时,验证精度最好。
3)BP 神经网络估测蓄积量时,采用植被指数参数作为变量效果最好;RBF 神经网络估测蓄积量时,采用19 个变量同时作为输入参数时,精度最高。
4)k-近邻法对森林蓄积量的估测效果最佳。估测蓄积量时,回归等数量化方法具有一定的缺陷,一方面此类方法采用的RS 和GIS 信息一般是建立在线性假设基础上的,对于非线性信息就无能为力了,另一方面参数回归是按照连续曲线或线进行拟合,总是下降或上升,造成较大误差。k-近邻法避免了上述缺陷,错误率在两倍贝叶斯决策方法的错误率范围之间。因此,在进行森林蓄积量遥感估测时,k-近邻法的精度最高,效果最佳,应当选取k-近邻法进行估测。
[1] 孙海鹏,包占青,姜志强.林木蓄积量预测[J].内蒙古林业调查设计,1999(3):106-109.
[2] 丛沛桐,祖元刚,王瑞兰,等.GIS 与ANN 整合技术在森林资源蓄积量预测中的应用[J].地理科学,2004,24(5):591-596.
[3] 李崇贵,赵宪文,李春干.森林蓄积量遥感估测理论与实现[M].科学出版社,2006.
[4] 侯长谋,杨燕琼,黄平,等.基于RS_GIS 的马尾松林分蓄积量判读模型研究[J].林业资源管理,2002(5):55-57.
[5] 国庆喜,张锋.基于遥感信息估测森林的生物量[J].东北林业大学学报,2003,31(2):13-16.
[6] 刘志华,常禹,陈宏伟.基于遥感、地理信息系统和人工神经网络的呼中林区森林蓄积量估测[J].应用生态学报,2008,19(9):1891-1896.
[7] Krasnopolsky V M,Chevallier F. Some neural network applications in environmental sciences. part II:advancing computational efficiency of environmental models[J]. Neural Networks,2003(16):335-348.
[8] 王改良,武妍.用入侵的自适应遗传算法训练人工神经网络[J].红外与毫米波学报,2010,29(2):136-139.
[9] 琚存勇,蔡体久.用泛化改进的BP 神经网络估测森林蓄积量[J].林业科学,2006,42(12),59-62.
[10] 高丹,迟道才,王铁良.基于MATLAB 神经网络的水稻需水量的预报模型[J].沈阳农业大学学报,2005,36(5):599-602.
[11] 邓立斌,李际平.基于人工神经网络的杉木可变密度蓄积量收获预估模型.西北林学院学报,2002,17(4):87-89.
[12] 李际平,邓立斌,何建华.基于人工神经网络的森林资源预测研究.中南林学院学报,2001,21(4):19-22.
[13] 许东,代力民,邵国凡,等.基于RS、GIS 及k-近邻法的森林蓄积量估测[J].辽宁工程技术大学学报:自然科学版,2008,27(2):195-197.
[14] 张凯,王润元,王小平,等.黄土高原春小麦地上鲜生物量高光谱遥感估算模型[J].生态学杂志,2009,28(6):1155-1161.
[15] 李晓松,李增元,高志海,等.基于NDVI 与偏最小二乘回归的荒漠化地区植被覆盖度高光谱遥感估测[J].中国沙漠,2011,31(1):162-167.
