露天转地下开采方案多目标决策分析
2014-03-04刘建东
陈 何,刘建东
(北京矿冶研究总院,北京100160)
矿山开采技术经济评价除了涉及一些可定量分析的指标外,还包括一些仅能定性分析的问题,如环境、安全等方面的评价指标,这就要求所选择的决策方法能适应各种可定量与不可定量的决策变量。多目标决策方法把目标体系结构予以展开,求得目标与决策方案的计量关系,在决策过程中认真考虑和衡量指标的相对重要性。露天转地下开采方案选择涉及多个决策变量,层次分析法(AHP)是一种较适宜的方法[1-2]。
1 多目标决策
1.1 决策变量的归一化处理方法
传统多目标决策时,数据一般采用线性函数转换法进行归一化处理[3]:

式中:x、y分别为转换前、后的值;MaxValue、MinValue分别为某项指标集中的最大值和最小值。
在仅有两个方案参与多目标决策的情况下,采用该方法时,无论两个方案的某项指标有多接近,只要其值不等,则归一化结果必为0或1,归一化结果为两种极端情况。显然,这种情况下的归一化过程中对指标的优劣性进行了“放大”,即得到了“好的更好、坏的更坏”的归一化结果,因此在实际应用中有一定的局限。鉴于此,引入 “差值比较算法”的概念,对指标进行归一化处理。
令I1= {越小越好的指标},I2= {越大越好的指标},I3={要求某一理想值的指标},I1∪I2∪I3=I,且Is∩It=φ(s≠t,s、t=1,2,3)。根据露天转地下开采方案决策问题的特点,以最终决策评分值最大者为最优方案,因此可令:
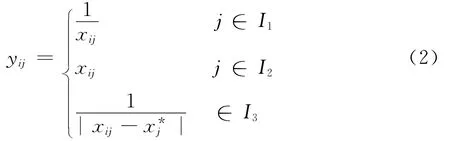


式中:Zst为优越度指标;ysj为s方案指标j的评分值;ytj为t方案指标j的评分值。
式(3)即为“差值比较算法”的归一化公式,式中|Zst|≤1。显然,Zst的符号代表了不同方案在某项指标上的优越性:若Zst>0,则在指标j上方案s优于方案t;若Zst=0,则在指标j上方案s同于方案t;若Zst<0,则在指标j上方案s劣于方案t。而|Zst|的值则代表了不同方案在某项指标上的优越度(即优越多少)。
因|Zst|≤1,可将区间[0,1]平分为9个等长度的区间,每个区间代表一个“优越等级”,依据|Zst|值所落入的区间选择相应的优越等级,如表1所示。

表1 优越等级标度区间Table 1 Superior rating scale interval
1.2 决策目标与变量
本次决策的目标是从无底柱分段崩落法开采方案和阶段连续崩落开采方案两种方案中,选取一种最优方案。
决策变量包括总投资、总利润、矿石成本、采场劳动生产率、矿块生产能力、矿石贫化率、矿石回收率、采切比、回采工艺难易程度、采场稳定性、作业安全性、采场通风条件等12个指标。这些指标均为开采方案所涉及的矿体开采范围和开采年限内的指标。
1.3 决策层次
决策层次共分四层。最上面为目标层,最下面为方案层,中间两层为准则层,如图1所示。
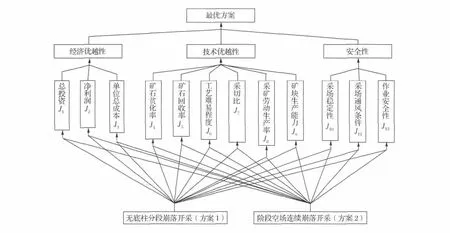
图1 多目标决策层次结构Fig.1 Multi-objective AHP decision structure
2 判断矩阵构建
2.1 第一准则层的判断矩阵
第一准则层包含经济优越性、技术优越性和安全性三个决策变量。矿山开采方案一般都建立在技术可行的原则上,而经济指标对矿山企业而言至关重要,但无论任何方案都应贯彻“安全第一”的原则。三个指标相比而言:安全性最重要、经济优越性次之、技术优越性居最后。依据指标的相对重要性建立判断矩阵,见表2。
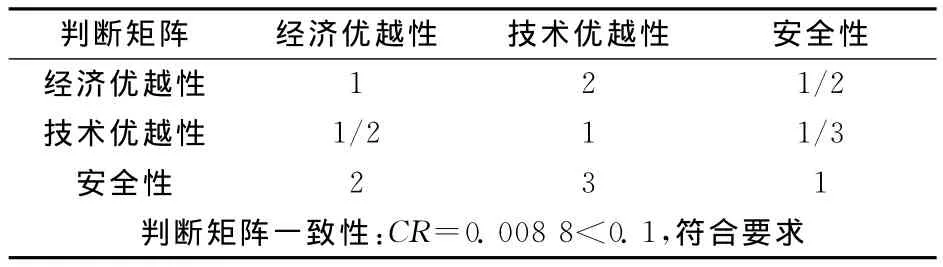
表2 最优方案判断矩阵Table 2 The judgment matrix of optimal scheme
2.2 第二准则层的判断矩阵
第二准则层受第一准则层支配,故可分为三部分内容:
1)经济优越性的判断矩阵:评判指标包含总投资、总利润、总成本。对于矿山企业而言,获取利润是其主要的目标,且企业对控制成本比较敏感。三项指标相比较而言:总利润最重要、总成本次之、总投资居最后。根据三个指标的相对重要性构建判断矩阵,见表3。
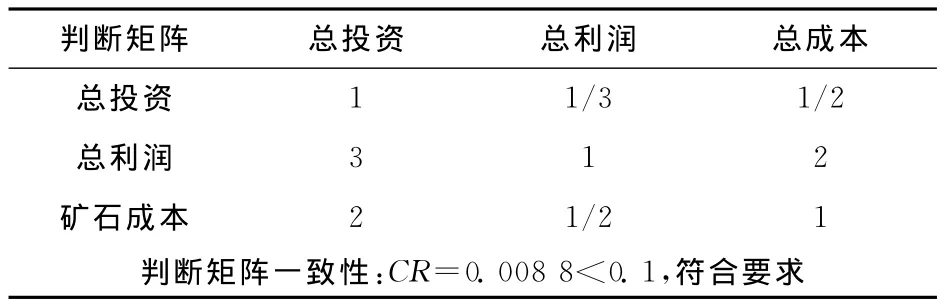
表3 经济优越性判断矩阵Table 3 The judgment matrix of economic superiority
2)技术优越性的判断矩阵:评判指标包含矿块生产能力、矿石贫化率、矿石回收率、采矿劳动生产率、采切比、工艺难易程度共6个指标。按照行业专家打分的方法,依次对各指标的重要程度进行评分,结果如表4所示。按各指标评分的大小构建技术优越性的判断矩阵,如表5所示。

表4 采矿技术指标重要程度评分Table 4 The importance ratings of mining technical index
3)安全性评价的判断矩阵:评判指标包括采场稳定性、采场通风条件、作业安全性共3个指标。采场稳定性属于可控的因素,其重要性比作业安全性应低一些;采场通风条件属辅助性因素,在三个指标中其重要性最低。三个指标的重要程度依次为作业安全性、采场稳定性、采场通风条件。按三个指标的相对重要性,构建安全性的判断矩阵,见表6。

表5 技术优越性判断矩阵Table 5 The judgment matrix of technology superiority
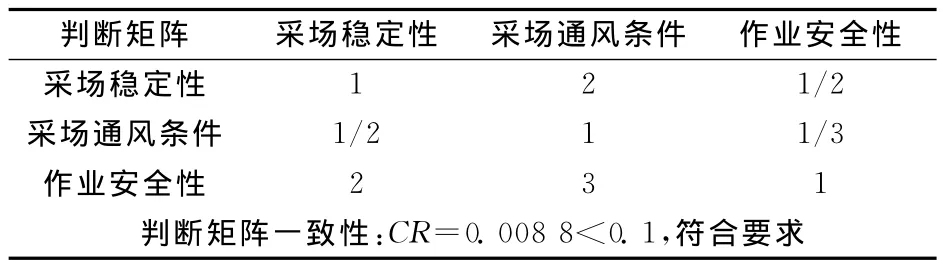
表6 安全性判断矩阵Table 6 Security judgment matrix
2.3 方案层决策指标计算及标度值
方案层为两种开采方案:即无底柱分段崩落开采方案和阶段空场连续崩落开采方案。对于可量化计算出的指标,需将其转化为可以用1~9标度的“重要程度”来描述的变量。露天转地下开采方案多目标决策(第二准则层)的12个评价指标中,矿石贫化率和回收率属于应尽可能靠近某一理想值(分别为0和1)的指标;其它可以量化的指标某些属于越高越好,某些则属于越低越好,各项指标按公式(1)至公式(3)进行归一化计算,结果得到Zst;对于工艺难易程度(J6)、采场稳定性(J10)、作业安全性(J11)和采场通风条件(J12)这四个无法直接定量计算的指标,主要采用定性分析的方法确定其标度。
工艺难易程度:无底柱分段崩落法应用广泛,技术较为成熟。阶段空场连续崩落采矿法技术要求相对较高,工艺更复杂。
采场稳定性:这一指标主要取决于矿岩条件。无底柱分段崩落法回采过程中不留矿柱,回采过程连续化;而阶段空场连续崩落采矿在初期回采矿房时暂留顶柱和间柱,在采场整体崩落时将顶柱和间柱一同崩落。阶段空场连续崩落采矿法的采场稳定性比无底柱分段崩落法略差些。
作业安全性:对于阶段空场连续崩落法,在专门设计或支护的凿岩硐室内作业,则安全性较好;无底柱分段崩落法工作面为巷道中,稳定性较好,但工作面处于经常移动状态,地压变化较快,对安全工作要求较高。
采场通风条件:阶段空场连续崩落采矿法的凿岩和出矿作业工作面均有贯通风流,通风条件较好;无底柱分段崩落法在独头巷道端部作业,通风条件较差。通风条件上阶段空场连续崩落法比无底柱分段崩落法要好得多。
将技术方案各项指标进行归一化计算,得到Zst,并根据表1选择判断矩阵值,分别列于表7中。

表7 决策指标标度值Table 7 AHP scale value
3 决策排序与结果
3.1 层次单排序
层次单排序就是指根据判断矩阵计算对于上一层某因素而言本层次与之有联系的因素的重要性次序的权值。可以归结为,求解矩阵的最大特征值和对应的特征向量,即对判断矩阵B,计算满足正式的特征根与特征向量:

式中,λmax为B的最大特征根;W为对应于λmax的正规化特征向量;W的分量Wi即是相应因素单排序的权值。
3.2 层次总排序
确定某层所有因素对于总目标相对重要性的排序权值过程,称为层次总排序。这一过程是最高层次到最低层次逐层进行的。对于最高层次下面的第二层,若上一层次A包含m个因素A1,A2,…,Am,其层次总排序权值分别为a1,a2,…,am,下一层次B包含n个元素B1,B2,…,Bn,它们对于因素Aj的层次单排序权值分别为bj1,bj2,…bjn(当Bi与Aj无联系时,bji=0),此时B层次总排序权值见表8。

表8 层次总排序表Table 8 Ordering for all hierarchy
3.3 一致性检验
为评价由判断矩阵求出的特征向量(权值)是否合理,对判断矩阵进行一致性随机检验。随机一致性比率:

式中,CI为判断矩阵的一致性指标;RI为平均随机一致性指标。
根据式(4)、式(5)及表8,决策结果如表9所示:方案1最终得分0.425 7,方案2最终得分0.574 3。因此,在综合考虑技术经济及安全性的情况下,阶段空场连续崩落开采方案要优于无底柱分段崩落开采方案。
4 结论
综合考虑技术、经济及安全等方面的评价指标,进行层次分析决策,认为阶段空场连续崩落法较无底柱分段崩落法更适用于露天转地下大规模开采。但从我国矿山生产实践看,无底柱分段崩落法与阶段空场连续崩落法均是适用于露天转地下大规模开采的采矿方法[4-5]。露天转地下开采是一项复杂的系统工程,涉及到过渡期产量衔接、覆盖层的形成、开拓系统衔接、露天残矿回采、坑内通风与排水等一系列问题,特别是矿山的投资情况、已有的开采技术条件等对最终决策起到重要作用,因而开采方案的选择需做大量的论证工作。
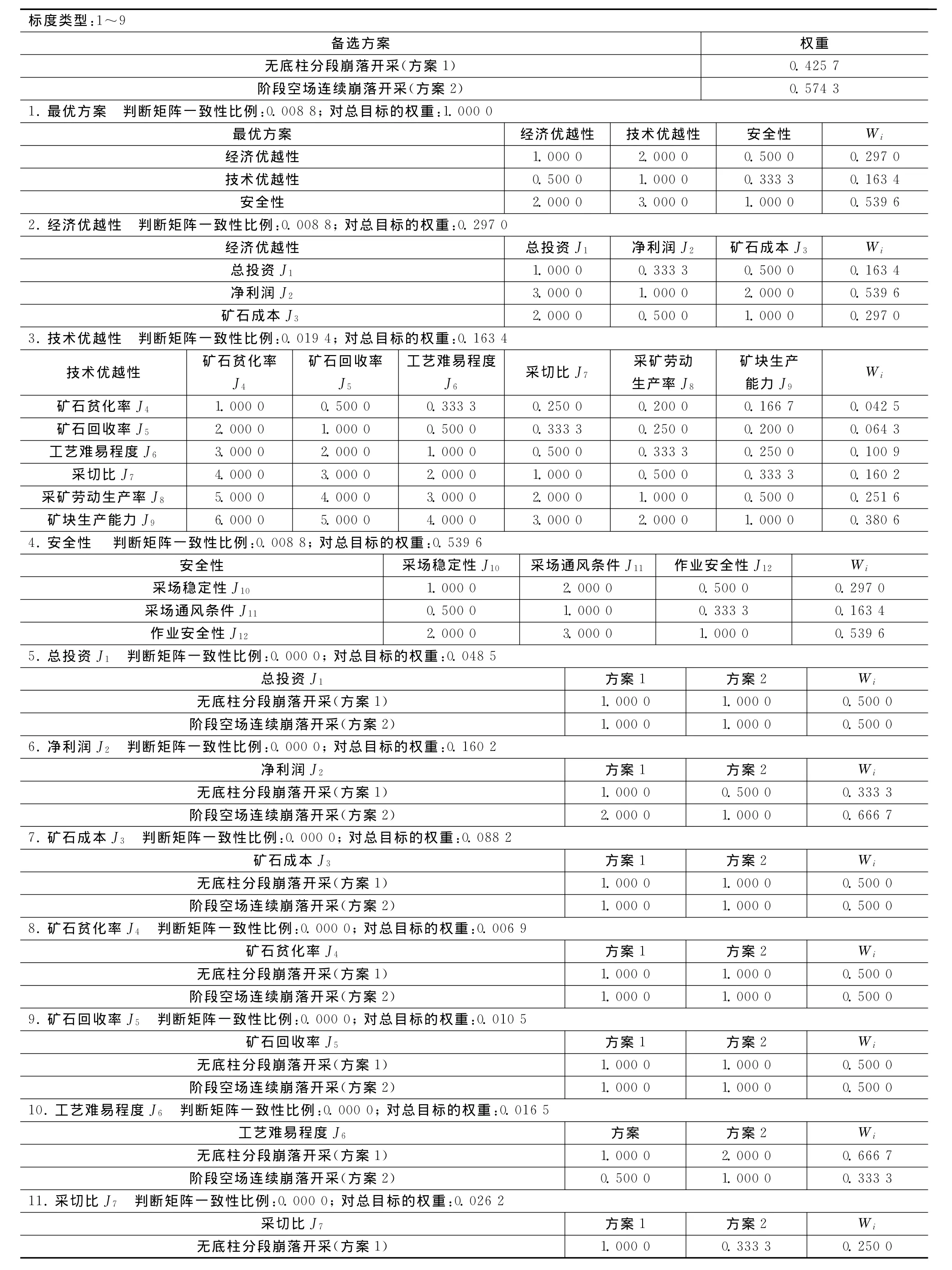
表9 多目标决策结果汇总表Table 9 Results of multi-objective decision

续表9
[1] 南世卿,任凤玉,宋爱东 .露天转地下开采过渡前期高效开采方案研究[J].中国矿业,2012,21(增刊1):343-346,383.
[2] 王新民,赵建文,张钦礼,等 .露天转地下最佳开采模式[J].中南大学学报:自然科学版,2012,43(4):1434-1439.
[3] 许树柏 .层次分析法原理[M].天津:天津大学出版社,1988:6-25.
[4] 卢宏建,高永涛,吴顺川,等 .石人沟铁矿露天转地下开采生产规模优化[J].北京科技大学学报,2008,30(9):967-971.
[5] 杨 力,王新民,赵建文 .石人沟露天转地下采矿方法优化选择[J].金属矿山,2011(7):19-23.
