应用P-Fibonacci加密的模糊自适应水印算法

冯祥斌，陈永红

（华侨大学 计算机科学与技术学院，福建 厦门361021）

随着互联网技术的不断发展，数字信息的非法复制已经开始对多媒体信息的所有权构成威胁.研究者提出了使用数字水印来证明多媒体信息的所有权［1］.根据原始图像在嵌入阶段的处理方式的不同，水印系统可以分为空间域水印［2-3］和变换域水印［4-7］.由于直接作用于空间域而不需要经过变换，使得空间域水印技术复杂度相对较低.对于频域水印，水印是通过修改经过离散余弦变换（DCT）或者离散小波变换（DWT）得到的频带进行嵌入的.DWT具有良好的空间定位、频率扩展和多分辨率特性.此外，随着图像加密技术的发展，图像置乱技术已经成为安全传输和保密存储的重要手段之一.为了对图像的（x，y）位置进行置乱，Sharinger［8］提出了一种基于混沌Kolmogorov流方法，Miyamoto等［9］提出了非连续Baker变换，Zou等［10-11］提出了限制域方法.然而，以上方法是周期性的且具有一定的针对性.基于此，本文提出了一种基于P-Fibonacci加密的模糊自适应水印新算法.

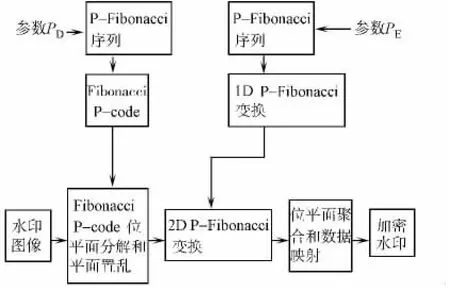
图1 仿真效果图Fig.1 Simulation effect diagram

1 置乱原理

借鉴递归序列的加密算法理念，对水印信息加密使用的是结合Fibonacci P-code位平面分解和P-Fibonacci变换的新型加密算法.该加密算法的流程图如图1所示.图1中：PD是分解参数；PE是加密参数.设计原理有如下3点.

1）将水印信息图像分解成Fibonacci P-code位平面，并打乱这些位平面的顺序.

2）基于2D P-Fibonacci变换对位平面的大小进行调整，对所有的位平面逐个进行加密.

3）结合所有已加密的位平面，并把这些图像数据映射回输入水印图像的原始数据范围内，得到最终的加密水印.

1.1 P-Fibonacci序列

P-Fibonacci序列是一种递归序列，其定义如下

式（1）中：i是序列的位置索引；非负数整数p是一个距离参数.

根据式（1），P-Fibonacci序列是随着p值变化而变化的，当p＝1时，其为经典Fibonacci数列.

1.2 1D P-Fibonacci变换

设Fp（i）和Fp（i＋1）是在式（1）中定义的P-Fibonacci序列的两个连续的元素.那么1D P-Fibonacci变换可以表示为

式（2）中：Fp（i）＋ε＜Fp（i＋1）提供了最小偏移量ε条件范围限定；N＝Fp（i＋1）-1指明了输入序列的最大值；非负整数i是P-Fibonacci序列的索引位置；常数ε是一个最小整数偏移量，使得Fp（i）＋ε和Fp（i＋1）的最大公约数是1.

1.3 2D P-Fibonacci变换

设A是一幅大小为M×N的2D图像，Cr与Cc分别表示行系数矩阵和列系数矩阵.那么2D P-Fibonacci变换可以表示为

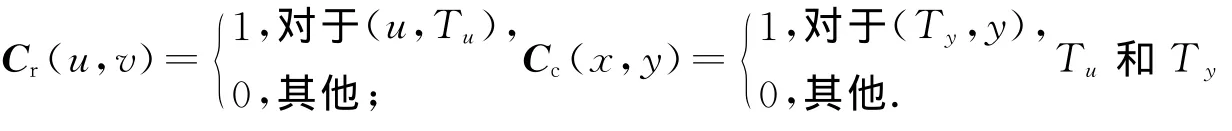
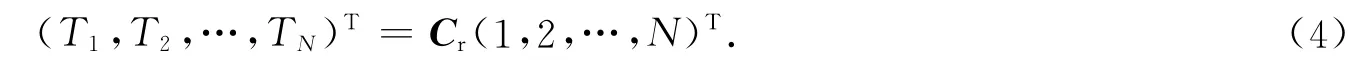
2D P-Fibonacci变换可以用于加密2D和3D图像.根据式（3）的定义，为了加密M×N的2D图像，行系数矩阵Cr必须是M×M矩阵，列系数矩阵Cr必须是N×N矩阵.

式（5）中：R为重构图像.

类似的，1D P-Fibonacci变换的逆变换可以定义为

2 Fibonacci P-code位平面分解

2.1 Fibonacci P-code

非负的十进制数D可以用以2为底的多项式表示为

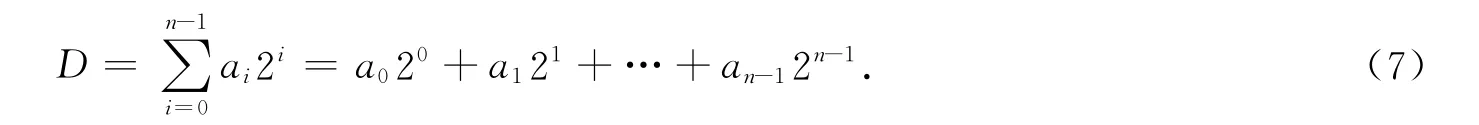
式（7）中：（an-1，…，a1，a0）是非负十进制数D的二进制表示.这个概念可以扩展到Fibonacci P-code，因此，Fibonacci P-code的定义为

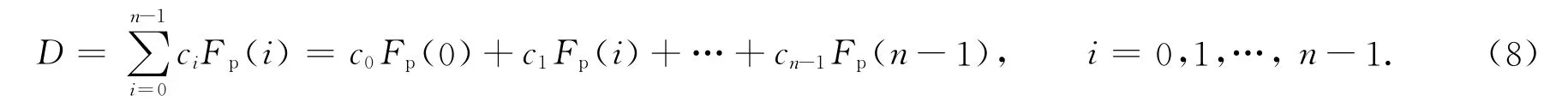
式（8）中：n和p是非负整数系数序列；ci∈（0，1）；（cn-1，…，c1，c0）成为D的Fibonacci P-code，即

式（9）中：p是式（1）中的P-Fibonacci序列的距离参数.

对于一个给定的p值，特定的十进制数的Fibonacci P-code并不是唯一的.为了使每个非负十进制数得到一个唯一的Fibonacci P-code，文中将采用文献［12］的规则来使Fibonacci P-code唯一，即

式（10）中：Fp（i）是式（1）在给定的p值下产生的P-Fibonacci序列的第i个元素（0≤i≤n）；非负十进制数s的前提是0≤s≤Fp（i-p）.

2.2 Fibonacci P-code位面分解

与传统的位平面分解方法类似，一幅图像也可以分解为多个Fibonacci P-code平面.Fibonacci P-code位平面的数量nB取决于图像的最大值Imax.为了使该分解方法能作用于所有的p值，设定p≤Imax，nB可以通过Imax计算得出；否则，如果p＞Imax，那么nB是通过p值进行计算得出.这表示在p＞Imax的情况下，Fibonacci P-code位面数仅由p值决定.对于一幅给定的灰度图像，Fibonacci P-code位平面分解的结果是由参数p的值决定的并且不同的p值对应的Fibonacci P-code位面的内容是不同的.这使得Fibonacci P-code位面分解更加适合于图像加密.

3 新型图像加密算法

P-Fibonacci加密算把原始图像分解成多个Fibonacci P-code位平面，打乱这些位平面的顺序，调整其大小以满足2D P-Fibonacci变换的大小要求，并通过2D P-Fibonacci变换对所有位平面进行加密.用式（7）定义的二进制码融合所有加密后的位平面，把这些图像数据映射回原始图像数据范围，可得到最终的加密图像.

用｛X0，X1，…，XL-1｝，X0＜X1＜…＜XL-1表示输入图像I（m，n）的离散强度级.当I（m，n）＝Xk，数据映射函数定义为

式（11）中：E为输出的加密图像；k＝0，1，…，L-1.

在重构加密图像时，授权用户必须拥有上述安全密钥和图像大小调整的方法.在解密过程中，P-Fibonacci加密算法首先把加密图像数据映射回原始数据范围；随后，将图像分解为二进制位平面（在加密过程中产生的Fibonacci P-code位平面），将所有位平面的顺序恢复到与原始顺序一致，使用2D Fibonacci变换对所有位平面进行解密，把所有位平面大小调整为原始大小；最后，组合所有解密后的位平面得到重构图像.

4 基于P-Fibonacci加密的水印算法

根据载体图像局部块纹理复杂度的不同，可以对水印的嵌入强度进行自适应的调整，这也能够使嵌入水印的鲁棒性和不可见性达到良好的平衡.因此，对图像块按照纹理复杂度的不同进行自适应模糊归类，可以分为3类：用S1表示纹理复杂度较低的类；用S3表示纹理复杂度较强的类；其他归类为S2.因为图像像素灰度的突变点可以用边缘点表示，图像块中的边缘点数量越多，纹理复杂度就越高.根据此性质，可以用边缘点的数量进行图像块的归类.

4.1 基于P-Fibonacci加密的水印嵌入流程

设水印的二值图像可以用矩阵表示为W＝｛w（x，y），1≤x，y≤M｝，其中w（x，y）表示水印图像在位置（x，y）的像素值.原始载体图像可以表示为F＝｛f（x，y），1≤x，y≤N｝，其中f（x，y）表示载体图像在位置（x，y）的像素值，并且N能被M整除.水印嵌入有如下4个步骤.

1）使用文中提出的P-Fibonacci新型图像加密算法对水印W进行加密，生成加密后的水印W′.

2）对载体图像F（x，y）进行分块处理，把原始图像分成N／（2M）×N／（2M）个大小为2M×2M的不相互覆盖的子图像，记作Bk，k＝0，1，…，N／（2M）×N／（2N）.每个子图像的边缘点数量为sum｛e（x，y）＝0，（x，y）∈Bk｝，其中e（x，y）是图像F（x，y）中提取的二值化边缘图的数学表示.分析每个子图像对3类的隶属程度，并根据最大隶属度原则进行归类，隶属函数表示为

式（12）中：i＝1，2，3.

根据各子块的边缘点数量进行统计并排序，用max表示边缘点数量最大值，用min表示数量最小值，T2为max和min的平均值；然后，根据各子块图像边缘点数量的分布情况设定T1和T3的阀值，并使得对S1类隶属度为1的数据都落在区间［min，T1］之内，对S3类隶属度为1的数据落在［T3，max］内，而用a1，a2，a3分别表示数据落在区间［T1，max］，［T1，T3］和［min，T3］的标准差.

3）对分类后的原始图像的子块Bk进行DWT变换，得到低频子带LLk，利用步骤2中的归类结果，根据人眼的视觉掩蔽特性，使嵌入水印的强度同图像子块的纹理复杂度成正比，达到自适应水印嵌入的效果，嵌入水印的方法可以为

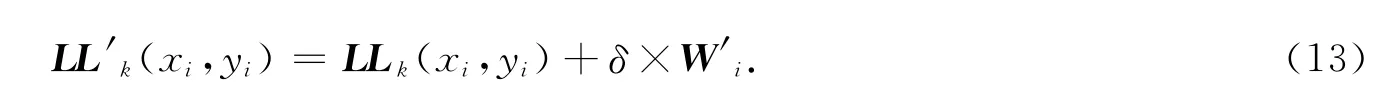
式（13）中：δ为自适应嵌入强度.

4）对各图像子块进行DWT反变换，重构得到嵌有水印的图像F（x，y）′.

4.2 基于P-Fibonacci加密的水印检测流程

作为水印嵌入的逆过程，水印的提取过程描述为以下5个过程.

1）对载入的原始图像进行分块分类处理，得到各分块的纹理复杂度隶属结果和相应的嵌入强度δ.

2）对原始图像的各个分块进行DWT变换，得到小波域的低频子带LLk.

3）对嵌入水印的图像F（x，y）′进行DWT变换，得到其小波域的低频子带LL′k.

4）利用假设检测的方法进行水印的检测，同时用前有水印的图像子块系数减去原始载体图像子块的系数再除以嵌入强度，从而提取出水印.

5）对水印信息图像实施P-Fibonacci算法的逆过程进行解密，得到加密前的水印信息，并把各个分块的N／（2M）×N／（2M）个水印进行叠加，对其进行求平均处理得到提取的水印图像.

5 实验仿真结果

实验采用的是大小为512 px×512 px的Lena的图像，如图2所示.水印信息使用的是64 px×64 px的二值灰度图像，如图3所示.

图2 仿真效果图Fig.2 Simulation effect diagram

图3 各种处理后的得到的水印Fig.3 Extracted watermark with various processing

通过统计各子块的边缘点数得到各类的嵌入强度，分别取δ1＝3，δ2＝5，δ3＝7.嵌有水印图像和原始图像的峰值信噪比RSN＝42.818 0，提取得到的水印和原始水印的相似度NC＝1，视觉掩蔽性良好.JPEG压缩处理后的数据图，如图4所示.从图4可知：即使在JPEG压缩因子小于20时（即压缩掉图像80%的信息），提取的水印信息仍然能够辨别并可以用来证明版权归属，此时对应的NC＝0.663 1.

添加椒盐噪声后的数据图，如图5所示.从图5可以看出：该算法对于椒盐噪声攻击具有良好的鲁棒性，即使在较大强度，如强度为0.12时，NC也能保持较大数值为0.905 6.

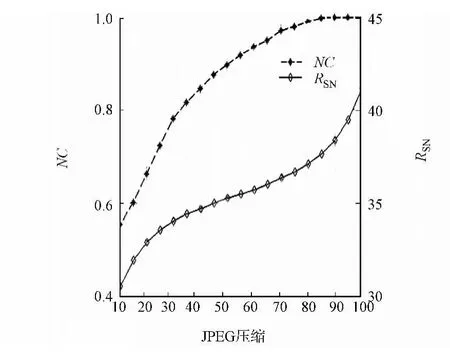
图4 JPEG压缩处理后的数据图Fig.4 Data figure with JPEG compression

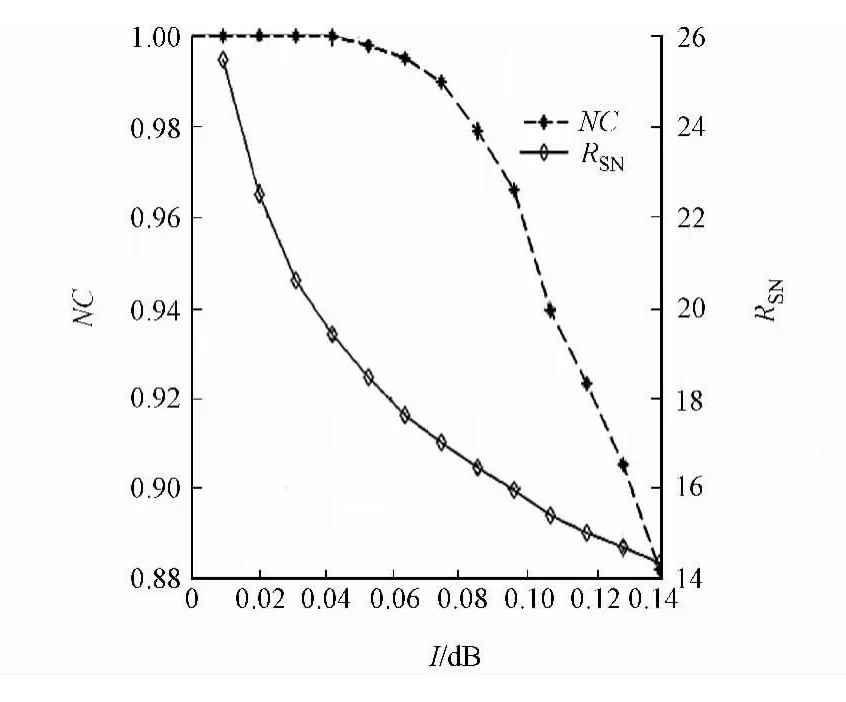
图5 添加椒盐噪声后的数据图Fig.5 Data figure with salt and pepper noise

常用攻击鲁棒性数据表，如表1所示.从表1可知：该算法对于中值滤波、高斯滤波、高斯噪声攻击具有很强的鲁棒性；水印提取后效果较好；对于几何攻击中的剪切有很好的抗攻击性能；当中心剪切为300×300的大小区域，NC值仍然能达到0.950 0；常用信号处理叠加后的攻击、常用信号处理与几何攻击（剪切）叠加后的攻击对嵌入水印后的图像进行攻击，提取的水印效果也较好，版权信息是可辨别的.

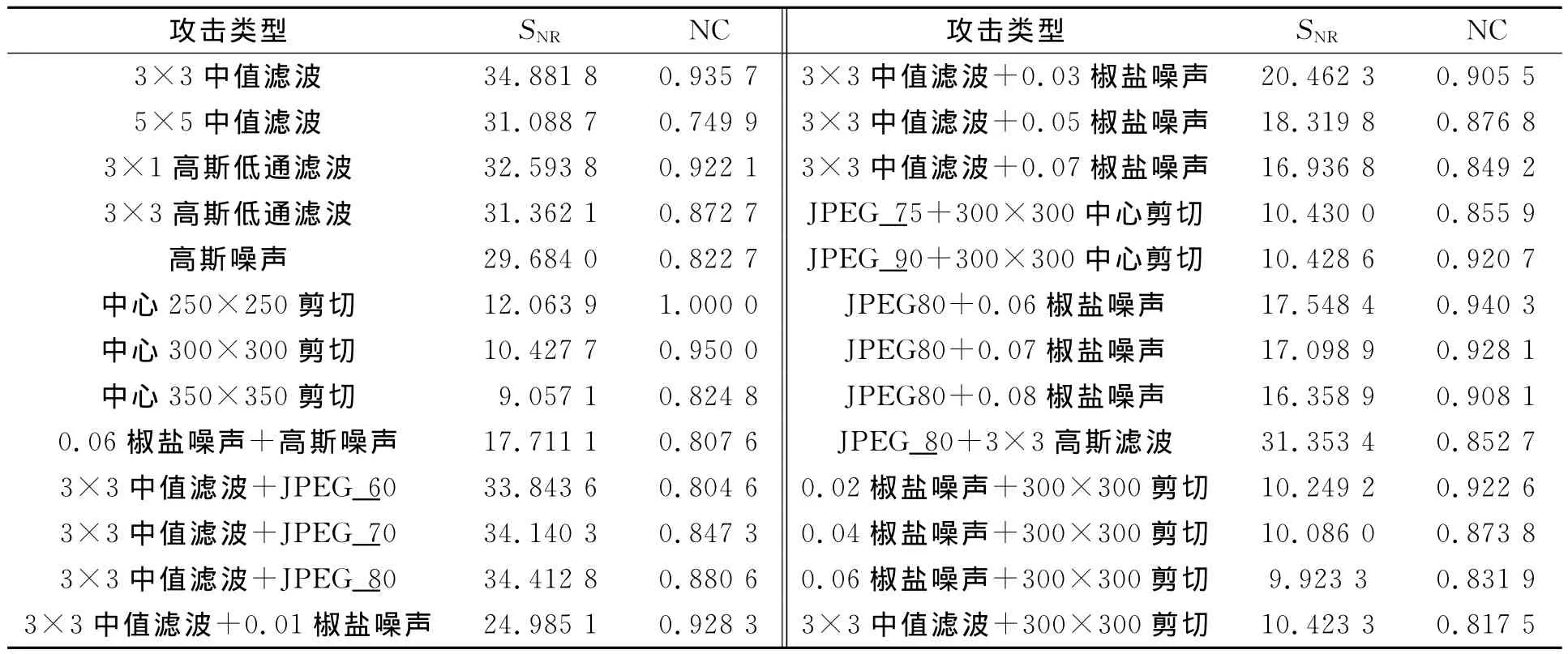
表1 常用攻击鲁棒性数据表Tab.1 Data table of the robustness with common attacks

6 结束语

P-Fibonacci算法对水印进行加密，极大地消除了二维数字水印图像的像素空间相关性，同时嵌入水印后的块效应降低，使算法抗攻击的能力和安全性增强.自适应模糊归类算法能够确定不同纹理复杂度的水印嵌入强度，使水印的不可见性保持良好的水平；而嵌入水印时采用重复嵌入的方式，也极大地增强了水印抗攻击的能力.实验结果表明：所提出的算法使不可见性和鲁棒性达到一个良好的平衡.

［1］ REZA M S，KHAN M S A K，ALAM M G R，et al.An approach of digital image copyright protection by using watermarking technology［J］.International Journal of Computer Science Issues，2012，9（2）：280-286.

［2］ MAO Jia-fa，ZHANG Ru，NIU Xin-xin，et al.Research of spatial domain image digital watermarking payload［J］.Eurasip Journal on Information Security，2011，2011（2011）：502748.

［3］ KIM J，WON S，ZENG Wen-jun，et al.Copyright protection of vector map using digital watermarking in the spatial domain［C］∥7th International Conference on Digital Content，Multimedia Technology and Its Applications.Busan：IEEE Computer Society Conference Publishing Services，2011：154-159.

［4］ HAN Wei-yuan，YAN Yang，ZHI Hui-lai.Digital watermark encryption algorithm based on Arnold and DCT transform［C］∥Proceedings of the 2011 International Conference on Electrical，Information Engineering and Mechatronics.Henan：Springer London Ltd，2012：613-621.

［5］ XU Tian-qi，CHANG Di，ZHANG Xia.A video digital watermarking algorithm based on DCT domain［C］∥2nd International Conference on Consumer Electronics，Communications and Networks.Three Gorges：IEEE Computer Society Conference Publishing Services，2012：1600-1603.

［6］ AGRESTE S，ANDALORO G，PRESTIPINO D，et al.An image adaptive，wavelet-based watermarking of digital images［J］.Journal of Computational and Applied Mathematics，2007，210（1／2）：13-21.

［7］ HABIBOLLAH D，MORTEZA M，AKHLAGIAN T F.Robust blind DWT based digital image watermarking using singular value decomposition［J］.International Journal of Innovative Computing，Information and Control，2012，8（7）：4691-4703.

［8］ SHARINGER J.Fast encryption of image data using chaotic Kolmogorov flows［J］.SPIE，1997，7（2）：318-325.

［9］ MIYAMOTO M，TANAKA K，SUGIMURA T.Truncated baker transformation and its extension to image encryption［C］∥Proceedings of SPIE on Advanced Materials and Optical Systems for Chemical.Boston：Society of Photo Optical，1999：13-25.

［10］ ZOU Jian-cheng，WARD R K.Some novel image scrambling methods based on chaotic dynamical system［C］∥Proceedings of the 9th Joint Inter Computer Conf.Zhuhai：IEEE Computer Society Conference Publishing Services，2003：188-191.

［11］ ZOU Jian-cheng，WARD R K.Introducing two new image scrambling methods［C］∥Proceedings of 2003 IEEE Pacific Rim Conference on Communications，Computers and Signal Processing.Victoria：IEEE Computer Society Conference Publishing Services，2003：708-711.

［12］ GEVORKIAN D Z，EGIAZARIAN K O，AGAIAN S S，et al.Parallel algorithms and VLSI architectures for stack filtering using Fibonacci P-codes［J］.IEEE Transactions on Signal Processing，1995，43（1）：286.