爆炸冲击波数值模拟及超压计算公式的修正

吴彦捷，高轩能

（华侨大学 土木工程学院，福建 厦门361021）

炸药爆炸的瞬时能释放巨大的能量并产生各种效应，但对建筑物破坏力最强、影响区域最大的是爆炸冲击波，而冲击波超压是评价炸药爆炸效应的重要参数之一.关于爆炸空气冲击波超压的计算，早期常用的经验公式有 GB 6722-2003《爆破安全规程》［1］、Henrych公式［2］、Sadovskyi公式［2-3］、Brode公式［4］、Aliansov公式［5］、Baker公式［6］等.20世纪末，不少学者也提出相应的计算公式［7-11］，但这些经验公式主要基于试验数据和理论分析结果得到，因爆炸作用的时程极短，爆炸冲击波迅速衰减，使实验结果的准确性受到影响.近年来，随着计算机技术的快速发展，数值模拟方法也愈来愈多地成为爆炸效应研究的重要手段，众多学者通过爆炸试验与数值模拟相结合的方法对冲击波超压进行一系列的研究，并提出相应的计算公式［12-21］.由前人的研究可知，爆炸数值模拟结果与理论值之间存在一定误差，且基于有限试验得到的若干爆炸冲击波经验公式适用范围和标准不一致，有必要对TNT炸药爆炸冲击波超压计算公式进行进一步修正.本文通过数值模拟结果与经验公式的对比分析，验证了计算模型及参数取值的可信性，提出爆炸冲击波修正计算方法.

1 爆炸冲击波超压ΔPf的计算

分别选取常用比例距离区段¯R＝0.3～1.0 m·kg-1／3及¯R＝1.0～15.0 m·kg-1／3，收集文献［1-21］中提到的冲击超压经验公式，对其进行对比分析，研究不同经验公式之间的误差.其中，文献［6-11］中的公式适用于高爆炸药的冲击波超压计算，文献［16-21］中的公式则是针对国防及核爆炸提出的，其余文献公式均适用于计算TNT炸药在无限空气中爆炸的冲击波超压.为便于参考比较，将各经验公式计算结果进行加权平均，设为平均值，并将平均值作为冲击波超压的中位值进行考虑，对比结果如图1所示.

冲击波超压平均值函数化表达式为

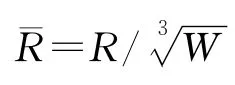
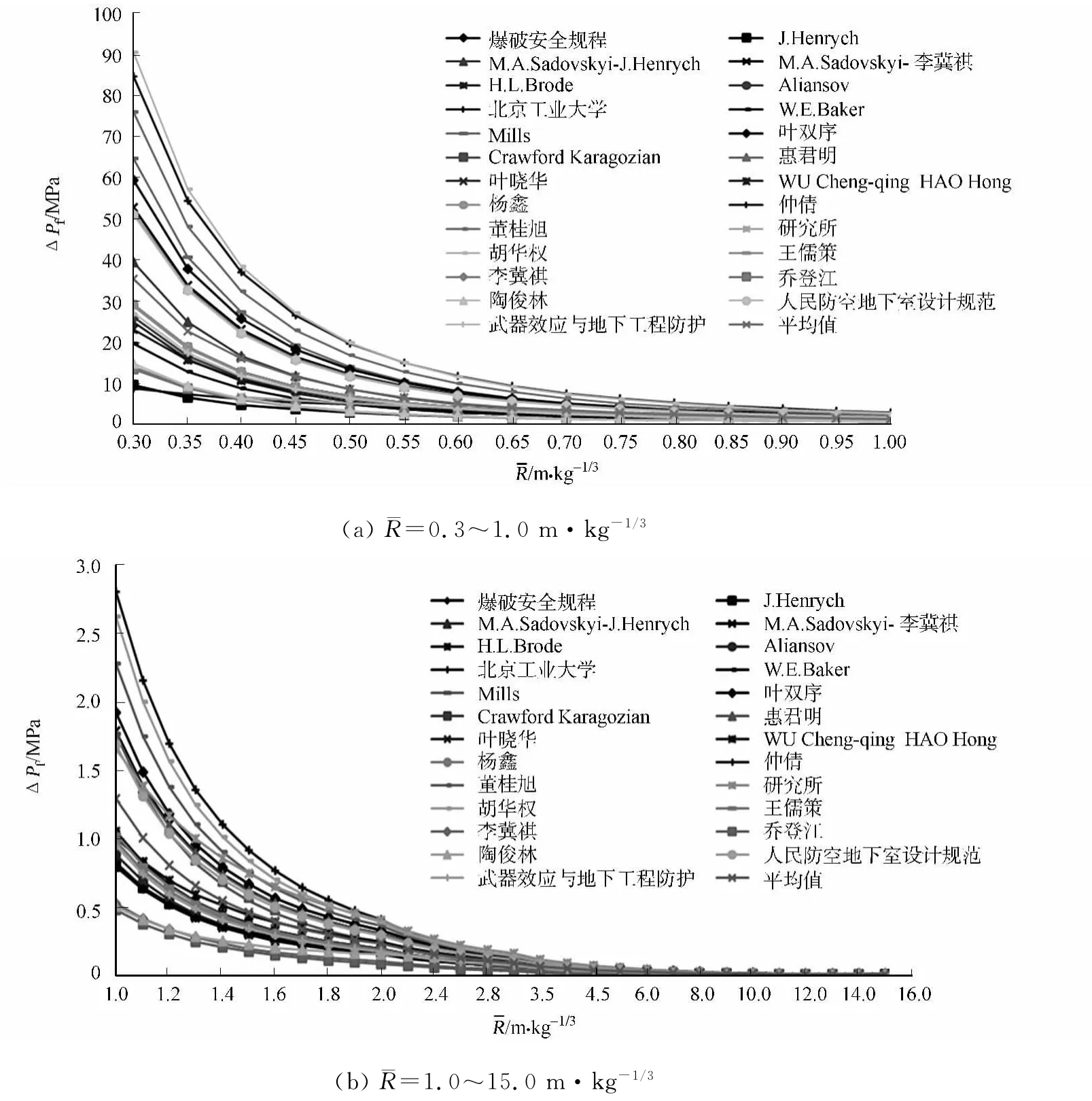
图1 经验公式的 ΔPf-¯R 曲线汇总Fig.1 ΔPf-¯R curves of all empirical formulae

由图1（a）可知：当比例距离为0.3～1.0 m·kg-1／3时，各经验公式总体变化趋势基本保持一致，随着比例距离¯R的增大，冲击波超压由于能量耗散而逐渐衰减.文献［6-11］提到的高爆炸药冲击波计算结果普遍大于平均值，而文献［16-21］针对国防及核爆炸公式计算结果则普遍低于平均值，这说明炸药性能及爆炸类型使冲击波超压计算结果之间存在偏差.当比例距离¯R＝0.3 m·kg-1／3时，各经验公式的最大值和最小值分别为90.5，8.69 MPa，之间相差近10倍，且与平均值35.3 MPa的相对误差达到-61.0%和75.4%，存在较大波动.在选取不同经验公式计算时，可能造成结果偏差过大，但Sadovskyi公式［2］计算结果与平均值较为吻合.因此，在比例距离¯R小于1.0 m·kg-1／3时，Sadovskyi公式［2］可以用于估算小范围内的爆炸冲击波超压.

由图1（b）可知：当比例距离¯R为1.0～15.0 m·kg-1／3时，早期常用经验公式的冲击波超压普遍低于平均值，处于经验公式的中位值或下位值.如果采用常用的经验公式对冲击波超压进行估算时，结果容易产生偏差，低估了爆炸冲击波的威力，导致计算结果安全性降低.当比例距离¯R＝1.0 m·kg-1／3时，各经验公式的平均值为1.29 MPa，而最大值和最小值分别为2.81，0.51 MPa，之间相对误差减小到-54.1%和60.5%.当比例距离¯R从0.3 m·kg-1／3变化到1.0 m·kg-1／3，相对误差呈现明显减小的趋势.随着比例距离¯R的增大，各经验公式计算结果逐渐趋于相近，相互之间的误差也逐渐减小.

通过以上分析可知：各冲击波超压经验公式之间均存在一定偏差，且适用范围不一致.这是因为早期的经验公式多数是通过爆炸试验测得，而在爆炸试验过程中，由于试验条件、测试范围的限制，以及地面或其他刚性物体产生的反射波效应，可能使冲击波超压得到增强，也使试验实测结果离散性较大.

2 TNT炸药爆炸数值模拟

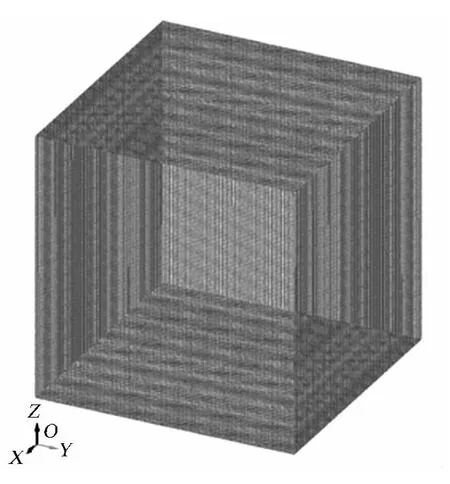
图2 空气与炸药的有限元模型Fig.2 Finite element model of explosive and air

2.1 材料参数取值

应用LS-DYNA有限元软件建立自由空爆模型.空气尺寸为20 m×20 m×20 m，炸药为立方体0.2 m×0.2 m×0.2 m，网格尺寸按0.2 m×0.2 m×0.2 m均匀划分.以炸药为中心取1／8模型进行计算，单元类型均为8节点3D-SOLID164，采用ALE（Arbitrary Lagrange-Euler）算法.在XOY，XOZ，YOZ平面采用对称约束，其他面采用透射边界以模拟无限空气域，空气与炸药有限元模型如图2所示.炸药和空气按均匀连续介质考虑，炸药采用MAT＿HIGH＿EXPLOSIVE＿BURN材料模型和JWL（Jones-Wilkins-Lee）状态控制方程，爆炸冲击压力［22］为

式（2）中：A，B，R1，R2，ω为输入参数；V为相对体积；E0为初始内能.TNT炸药的材料参数取值如下：炸药密度ρ为1 630 kg·m-3；炸药爆速D为6 713 m·s-1；爆压PCJ为18.5 GPa；A，B分别为540.9，9.4 GPa；R1，R2，ω分别为4.5，1.1，0.35；E0为8 GJ·m-3；初始相对体积V0为1.0.

空气采用MAT＿NULL空材料模型和线性多项式方程EOS＿LINEAR＿POLYNOMIAL，即

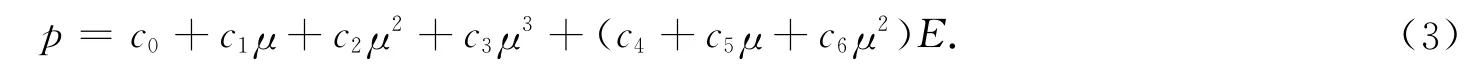
式（3）中：μ＝ρ／ρ0-1，ρ为空气质量密度，ρ0为参考质量密度；E为单位体积内能.线性多项式状态方程遵守 Gamma定律，c0，c1，c2，c3，c4，c5，c6为实常数.空气的材料输入参数如下：ρ为1.290 kg·m-3；c0～c3都为0；c4，c5都为0.4；c6为0；E0为0.25 MJ·m-3；V0为1.0.

2.2 数值模拟结果分析

由爆炸数值计算模型生成相应的K文件，将全部信息输入K文件，通过LS-DYNA求解器进行计算，运用常用后处理软件LS-PREPOST4.0对以上求解结果进行后处理；提取比例距离¯R＝0.6～1.0 m·kg-1／3及¯R＝1.0～6.0 m·kg-1／3范围内有限测点的冲击波超压.数值模拟结果，如表1所示.

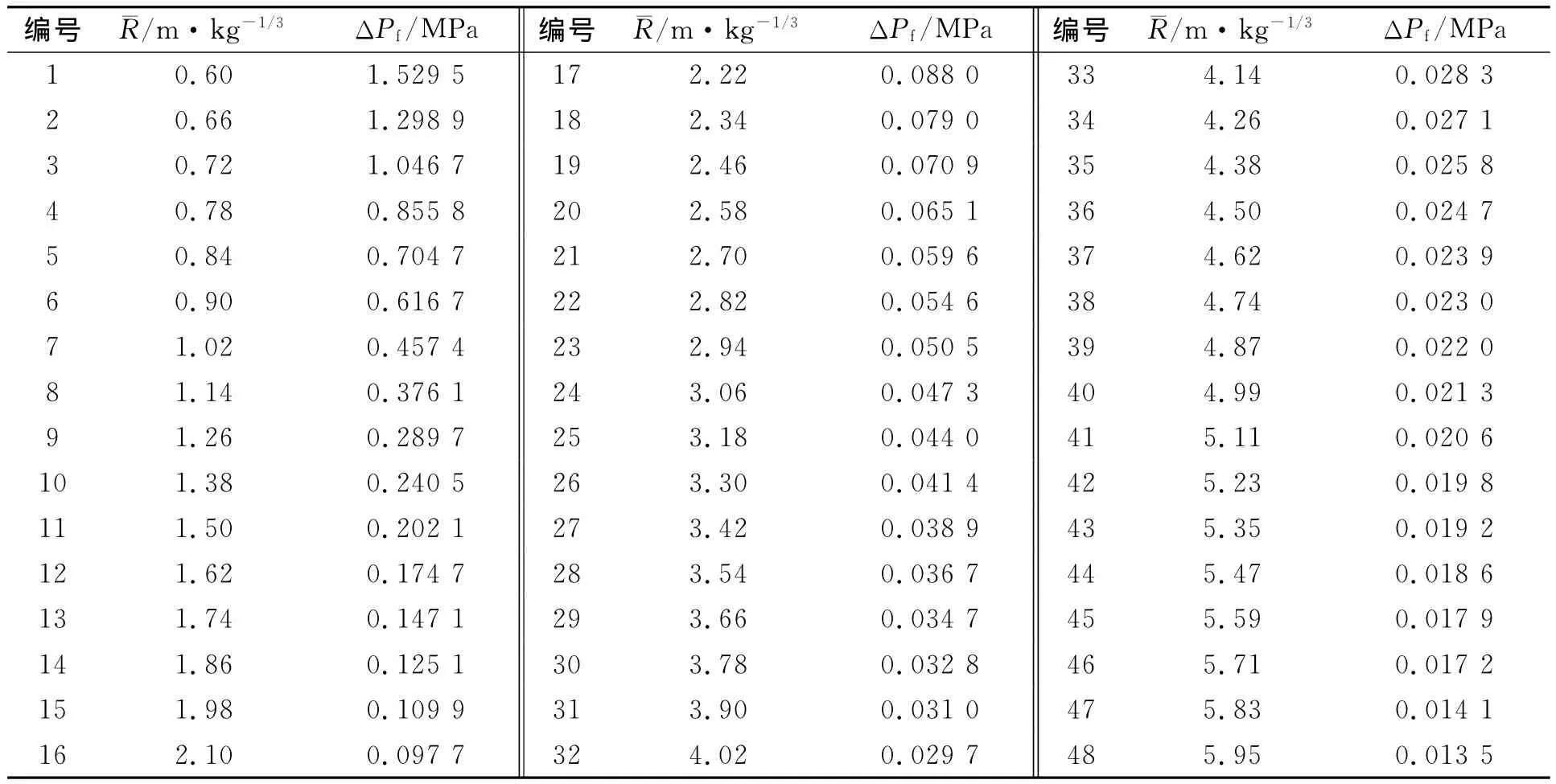
表1 冲击波超压数值模拟结果Tab.1 Numerical simulation results of shock wave overpressure

结合表1数值模拟结果，拟合得到冲击波超压计算公式，具体表达式为

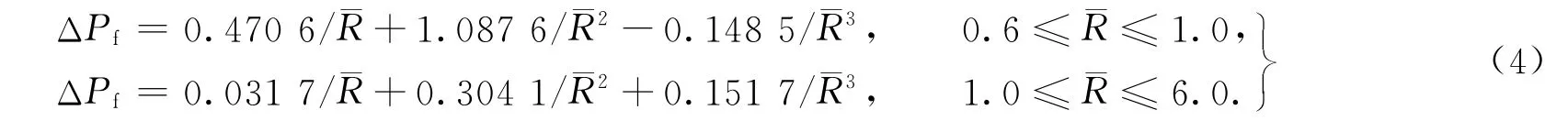
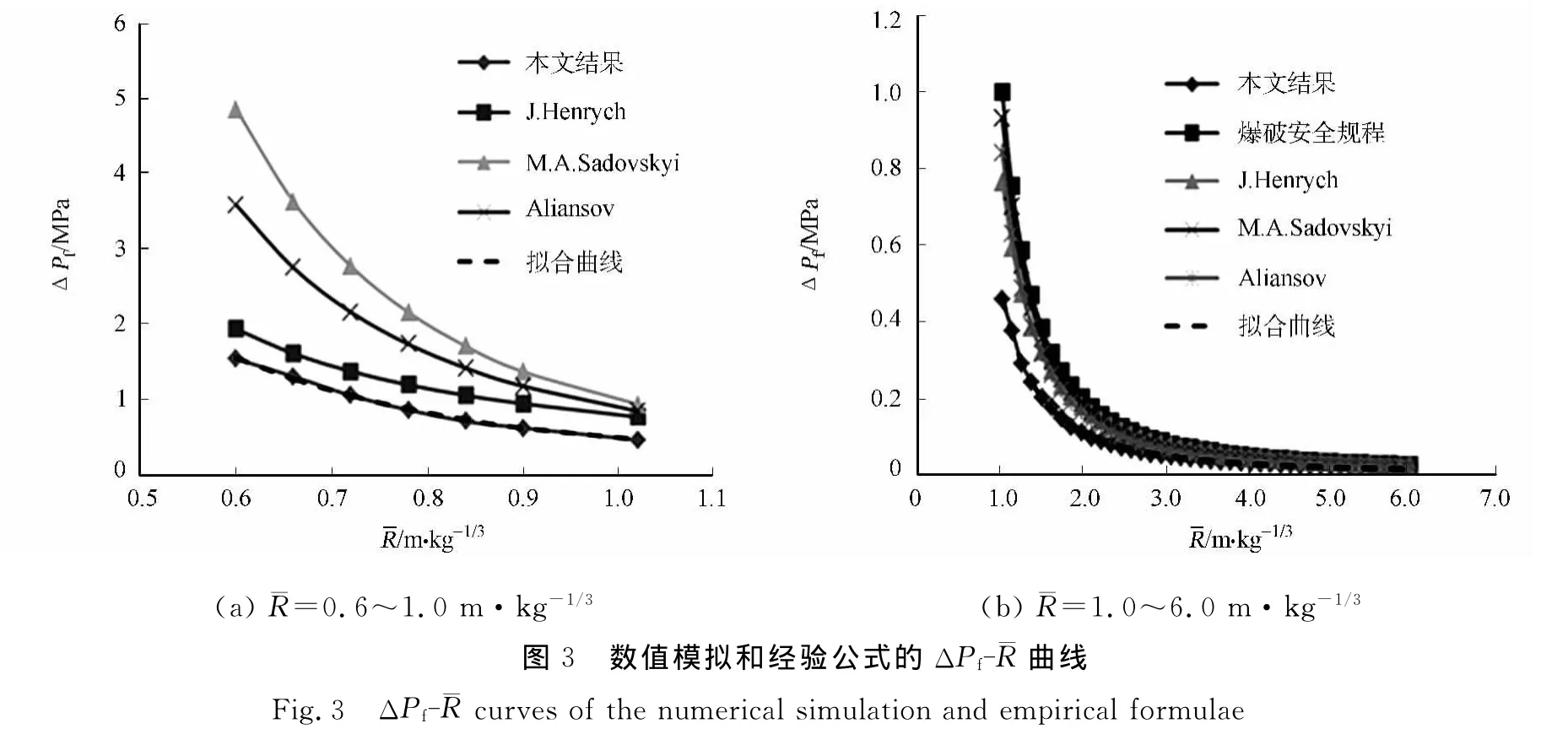
图3为冲击波超压数值计算结果与经验公式的比较，并给出了拟合曲线式（4）.由图3可知：数值模拟结果总体上与经验公式符合较好，且与Henrych公式最为接近，但均小于各经验公式计算结果.这是因为数值模拟计算基于理论状态方程建模，是理想状态的爆炸效应，得出的冲击波超压较试验数据偏小也是合理的.因此，数值模拟结果可以作为爆炸冲击波超压的下限值.随着比例距离¯R的增大，数值模拟结果与经验公式的误差逐渐减小.总体而言，数值模拟结果与经验公式的总体变化趋势一致且吻合较好，验证了计算模型与参数取值的可信性.

3 冲击波超压计算公式修正

已有的冲击波超压经验公式适用范围和标准不一致，且相互之间误差较大，通过数值模拟及经验公式计算结果进行对比分析，提出数值模拟的系数修正方法，并拟合出统一的爆炸冲击波超压计算公式.

3.1 冲击波超压修正计算方法

由图3可知：常用经验公式计算结果普遍处于冲击波超压的中位值或下位值，而数值模拟结果则处于下限值.与经验公式相比，数值模拟结果偏低，若抗爆设计过程中以数值模拟结果为依据进行设计时，有存在低估爆炸冲击波超压的危险.为了确保抗爆设计的安全性，在数值模拟结果ΔPf的基础上乘以一个修正系数ηp，得到修正后的冲击波ΔP′f，具体表达式为

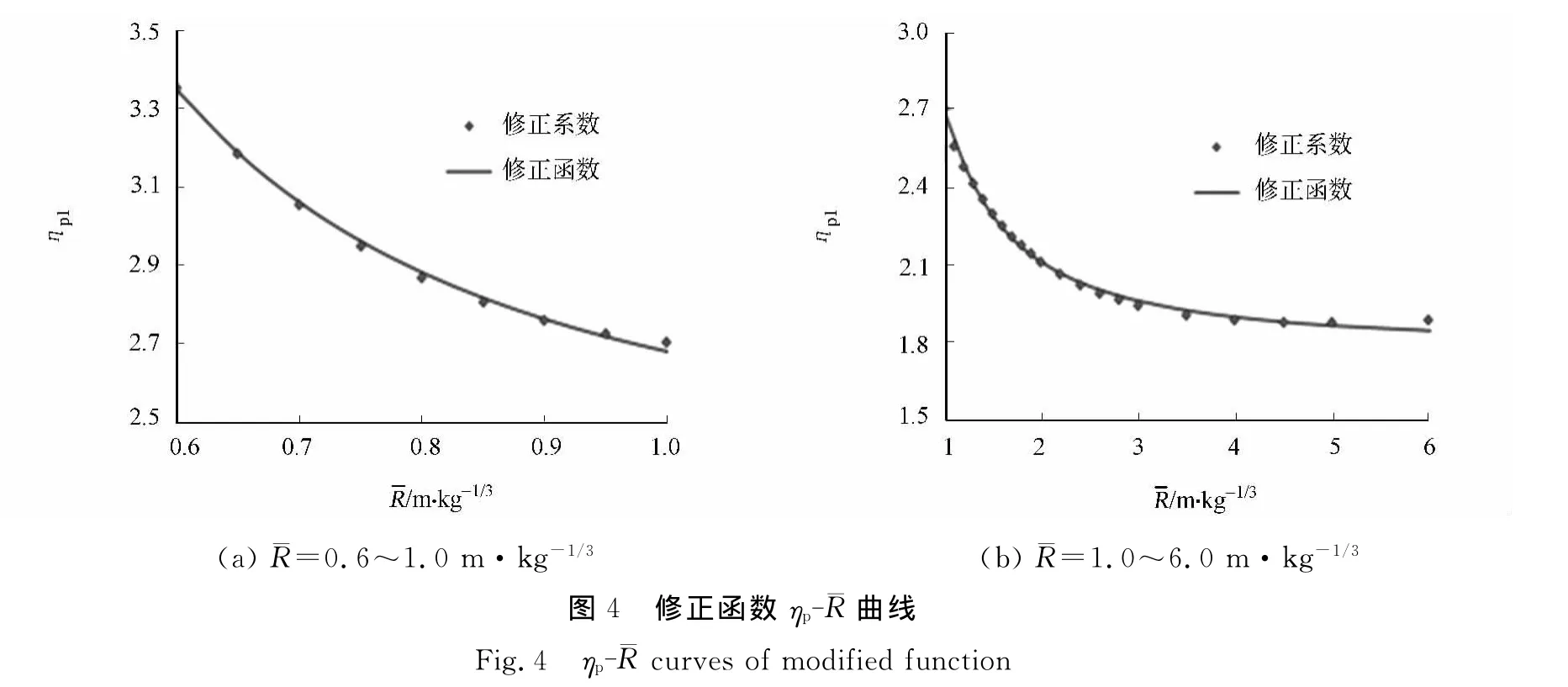
随着比例距离¯R的增大，数值模拟结果更为精确，即修正系数ηp与比例距离¯R成反比关系，且趋势逐渐平缓.因此，选用幂函数η＝a¯Rb＋c形式进行拟合能够准确地描述修正函数.

选取常用比例距离区段¯R为0.6～1.0及1.0～6.0 m·kg-1／3，对图1中的各经验公式进行加权平均，得到平均值ΔP′f，e，如式（1）所示.将ΔP′f，e作为参考，通过ΔP′f及ΔP′f，e求得ηp，利用修正系数对数值模拟计算结果进行修正，以求得到冲击波超压的中位值，使得修正后的ΔP′f接近ΔP′f，e.拟合得到修正函数如图4所示.

修正函数ηp具体表达式为

3.2 误差分析

作为参考，通过验证该修正计算方法的适用性，对修正函数进行误差分析，结果如表2所示.表2中：δ为ΔP′f和ΔP′f，e的相对误差百分比.从表2可知：相对误差δ基本控制在±1%范围内，只有少数超过±1%，拟合程度较高.说明通过上述修正计算方法能够有效地修正数值模拟计算结果，并得到冲击波超压的中位值，使得数值模拟结果能够有效地运用于抗爆设计中.

3.3 修正后的超压计算公式

通过以上提出的超压修正计算方法，得到统一的冲击波超压修正计算公式，具体表达式为

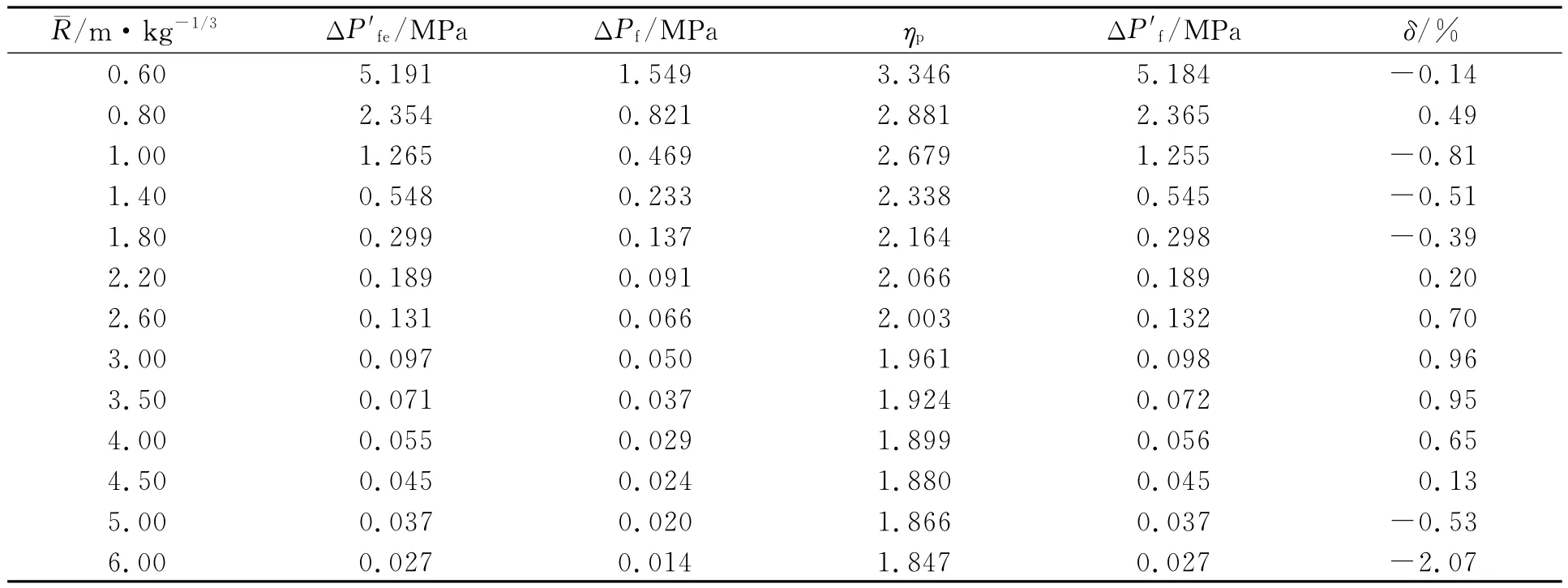
表2 修正函数ηp误差分析Tab.2 Error analysis of modified functionηp

4 结论

通过上述对TNT炸药爆炸数值模拟及冲击波超压计算公式的修正，可以得出以下3点结论.

1）早期常用的经验公式普遍处于经验公式的中位值或下位值，存在了低估爆炸冲击波的危险.在比例距离¯R小于1.0 m·kg-1／3时，Sadovskyi公式［2］可以用于估算小范围内的爆炸冲击波超压.

2）基于LS-DYNA有限元程序实现TNT炸药爆炸的数值模拟计算是可行的，且数值模拟计算结果可以作为爆炸冲击波超压的下限值.

3）通过冲击波超压公式修正计算方法对数值模拟结果进行修正，能够有效地提高数值模拟结果的可用性，提出统一的计算公式并得到冲击波超压中位值，为抗爆设计提供参考.

［1］ 国家质量监督检验检疫总局.GB 6722-2003爆破安全规程［S］.北京：中国标准出版社，2003：47.

［2］ 亨利奇J.爆炸动力学及其应用［M］.熊建国，译.北京：科学出版社，1987：127.

［3］ SADOVSKYI M A.Mechanical action of air shock waves of explosion，based on experimental data［M］.Moscow：Izd Akad Nauk SSSR，1952：1-2.

［4］ BRODE H L.Blast wave from a spherical charge［J］.Phys Fluids，1959，2（2）：217.

［5］ 李翼祺，马素贞.爆炸力学［M］.北京：科学出版社，1959：260.

［6］ BAKER W E.Explosions in air［M］.Austin：University of Texas Press，1974：6-10.

［7］ FAHMY A，TOLBA F.Response of FRP-retrofitted reinforced concrete panels to blast loading［M］.Canada：Carleton University，2001：12.

［8］ 叶序双，戴镇华，庄兆铃.非理想刚性地面球形装药爆炸冲击波超压的试验研究［J］.解放军理工大学学报：自然科学版，1988（4）：72-82.

［9］ 惠君明，陈天云.炸药爆炸理论［M］.南京：江苏科学技术出版社，1995：145-146.

［10］ 叶晓华.军事爆破工程［M］.北京：解放军出版社，1999：216-219.

［11］ WU Cheng-qing，HAO Hong.Modeling of simultaneous ground shock and air blast pressure on nearby structures from surface explosions［J］.Int J Impact Eng，2005，31（6）：699-717.

［12］ 杨鑫，石少卿，程鹏飞.空气中 TNT爆炸冲击波超压峰值的预测及数值模拟［J］.爆破，2008，25（1）：15-19.

［13］ 仲倩，王伯良，黄菊，等.TNT空中爆炸超压的相似律［J］.火炸药学报，2008，33（4）：32-35.

［14］ 董桂旭，杜茂华，黄雪峰.某型炸药的冲击波超压峰值计算公式参数的修正［J］.海军航空工程学院学报，2010，25（5）：542-544.

［15］ 胡华权，裴明敬，许学忠，等.燃料空气炸药爆炸威力评价方法研究［C］∥第四届全国爆炸力学实验技术学术会议.合肥：［出版者不详］，2006：313-318.

［16］ 王儒策，赵国志.弹丸终点效应［M］.北京：北京理工大学出版社，1993：45.

［17］ 乔登江.核爆炸物理概论［M］.北京：原子能出版社，1988：30-70.

［18］ 陶俊林，黎泽朋，陈小伟.核爆聚变电站发电时的冲击波超压传播规律［J］.高压物理学报，2012，26（2）：221-226.

［19］ 国家技术监督局，中华人民共和国建设部.GB 50038-2005人民防空地下室设计规范［S］.北京：中国建筑工业出版社，2006：161.

［20］ 王年桥.防护结构计算原理与设计［M］.南京：工程兵工程学院出版社，1998：176-178.

［21］ 樊海青.爆炸冲击波作用下多层多跨框架结构的塑性极限分析［D］.北京：北方工业大学，2009：21.

［22］ 段雷琳，高轩能，江媛.内爆炸下球面钢网壳结构的冲击波超压计算分析［J］.华侨大学学报：自然科学版，2013，34（5）：557-562.