基于Visual Basic编程对离心泵性能曲线的拟合

刘红明，孙 铁，刘 嵩，王 亮，魏佳广

（1. 辽宁石油化工大学 机械工程学院，辽宁 抚顺 113001； 2. 安阳工学院 工程训练中心，河南 安阳 455000；3. 中国石化沧州分公司，河北 沧州 061000； 4. 海洋石油工程股份有限公司，天津 塘沽 300452）

基于Visual Basic编程对离心泵性能曲线的拟合

刘红明1，孙 铁1，刘 嵩2，王 亮3，魏佳广4

（1. 辽宁石油化工大学 机械工程学院，辽宁 抚顺 113001； 2. 安阳工学院 工程训练中心，河南 安阳 455000；3. 中国石化沧州分公司，河北 沧州 061000； 4. 海洋石油工程股份有限公司，天津 塘沽 300452）

在分析拟合离心泵性能曲线必要性的基础上，以拟合离心泵流量和扬程性能曲线为例，介绍了利用最小二乘法使用visual Basic语言进行直接编程拟合曲线的方法；经实际使用本程序具有简单、易用、求解效率高、适用范围广等特点，有效解决了石化行业中离心泵选型、试验中曲线拟合的数据处理问题，可以在离心泵及容积泵性能曲线拟合中推广应用。

离心泵；性能曲线；最小二乘法；拟合曲线；Visual Basic

离心泵是石油化工行业中广泛使用的流体输送设备。在对离心泵系统优化运行分析和节能改造过程中， 常遇到离心泵的性能测定、选型计算和优化调度等问题。这些问题我们都需要以离心泵性能曲线为基础来解决。离心泵的性能曲线是在实验的基础上通过测定、绘制得到的。在绘制过程中由于实验过程以及实验设备存在误差会使曲线不平滑，出现畸变点，为绘制出准确的性能曲线常需要进行曲线拟合。离心泵的性能曲线反映了离心泵各性能参数之间的关系与变化规律，一般由离心泵设计部门或厂家以随机资料形式将采样点数据表格及绘制曲线提供给用户，但都没有给出性能曲线的函数表达式[1-3]。在具体研究中，已知性能曲线的前提下，当想知道性能曲线上具体点的对应值时就只能采用在曲线上取点估读的方法，这直接导致后续分析和研究的结果失真。因此为了得到更准确的结果，需要根据离心泵的试验数据即采样点数据表格中的数据进行性能曲线拟合以得到性能曲线的函数表达式从而得到准确的数据。

现以离心泵性能曲线中的流量和扬程曲线(Q-H曲线)为例，依据高斯马尔可夫定理—在给定经典线性回归的假定下，最小二乘估计量是具有最小方差的线性无偏估计量,所以运用最小二乘法拟合离心泵曲线。考虑到手工计算求解联立方程组工作量大，费时费力。实际研究中，多采用计算机利用MATLAB、SPSS 等计算软件进行求解，但这些软件多价格不菲，需经过专门学习不宜使用，且编程后计算以及曲线绘制仍必须依托其软件平台[4-7]；常用的C语言编程生成exe程序必须经过二次编译。所以这里笔者采用Visual Basic语言直接编程生成可直接在window系统下运行的exe文件，以求解并得到拟合后的曲线。

1 曲线拟合的方法

1.1 确定流量和扬程曲线(Q-H曲线)的形式

在使用最小二乘法拟合曲线时，确定曲线为何种形式是是整个过程的第一步也最重要，最关键得一步。离心泵的流量—扬程曲线的函数表达式主要有以下几种形式[1-4]:

式中：H ——离心泵扬程，m；

Q ——离心泵流量，m3/h；

a, k ——模型待定系数；

m ——列宾宗公式中指数。

式中：H ——离心泵扬程，m；

Q ——离心泵流量，m3/h；

k, m ——模型待定系数。

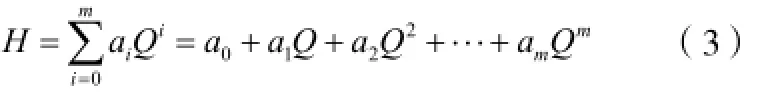
式中：H ——离心泵的扬程，m；

Q ——离心泵的流量，m3/h ；

ai——回归系数， i =0，1，2，…，n。

式(1)为幂函数形式，式(2)为指数函数形式，最小二乘法拟合函数时必须首先将函数线性化[8-10]，这在实际编程中，将使得变量定义及求解变得更复杂，工作量将变得较式(3)多项式形式更大；而由文献[2]采用多项式函数形式为数学模型得到的拟合曲线在工作区内与实测特性曲线基本重合，而公式1的误差则为2%左右。故本文选取离心泵的流量-扬程函数表达式的多项式形式建立数学模型，对求解从而得出离心泵的流量-扬程函数表达式。

1.2 确定采样点数据数量即变量对应的数据

选定拟合曲线的形式为多项式形式后，则变量数据为流量Q，扬程H，确定需要拟合的采样点数据数，采样点不能少于5组。

1.3 确定所要拟合曲线所建立的法方程组

依据最小二乘法的一般提法[8-10]：对给定的一组数据（xi,yi）及权系数wi（i=0,1,2,…,m）在函数类中，则相当于求该函数的最小值问题，由多元函数求极小值的必要条件最终求解最即为所求。

1.4 使用Visual Basic语言编程实现曲线拟合及方程求解

当用多项式做最小二乘法时，用高次（一般大于等于7时），往往会使得法方程是病态方程组，这会使得方程组的解有较大误差[8]；而拟合次数为1次时，曲线为直线，这显然不符合离心泵性能曲线的曲线形式。所以笔者在采用Visual Basic语言编程时将拟合次数限定于7次至2次拟合，并设计程序窗口使拟合次数可调，使用者可以根据自身需要以及绘图框生成的拟合后曲线是否良态来选取适当的拟合次数。

1.4.1 编程过程

文中考虑到篇幅关系程序代码从略。

(1) 在 VB 6.0环境中新建一个标准工程，然后对窗口进行设计。为满足设计的基本目标，窗口分为绘图框PictureBox、求解公式显示框TextBox、求解次数选框ComboBox等。考虑到离心泵性能曲线的采样点数据通常较多，将数据处理窗口设计为载入txt文件，采样点数据显示在MSFlexGrid框中。这样每次试验后，只需用txt文档记录数据，简单易用、占用内存小而且便于数据处理。

(2)窗口设计好后，就需要依据已选定的函数形式建立数学模型，以设计程序代码以求解数据。为使程序代码尽可能简洁，且减少对其他程序模块的依赖性，程序核心的函数即算法部分笔者采用自己设定而不是调用其它程序中的函数及功能模块。笔者对此程序中函数部分采取了如下编程思路：

a. 定义方程中各变量，形成法方程组中的各元素；

b. 写出法方程组；

c. 求解法方程组并输出至窗口。

(3)考虑到曲线是基于采样点经方程求解后得出，笔者将采样点的线宽设置为5且为绿色，而将曲线设置为1，这样点在图像中醒目且当曲线偏离采样点时即说明误差较大，可以考虑舍去不在线上的畸点。绘制曲线的具体代码属于VB语言中的picture命令，相对定义并求解法方程组代码较为简单。

1.4.2 输出 exe文件

在结束上述编程过程后，对工程进行调试运行，对发现的问题进行修改，并对工程窗口界面进行仔细调整，设置程序图标。最终输出可执行exe文件。

2 应用实例

2.1 对EH100-80-2315型离心泵的曲线拟合

2.1.1 全数据拟合

在对某石化厂常减压装置EH100-80-2315型离心泵进行节能改造过程中，为得到准确的Q，H值，现应用本程序对其性能曲线进行拟合并求解出方程。离心泵在工作转速下实验数据如表1。

表1 离心泵流量扬程采集值表Table 1 Centrifugal pump Q – H measured value table

使用程序载入txt格式原始数据文件，选取拟合次数为3次，4次，5次，6次；分别点击曲线拟合按键，可直接得到拟合后的曲线及本型号离心泵流量和扬程曲线方程。由拟合曲线的形式我们可以看出3点为畸点，当拟合次数高于4次时，曲线畸形(图1）。

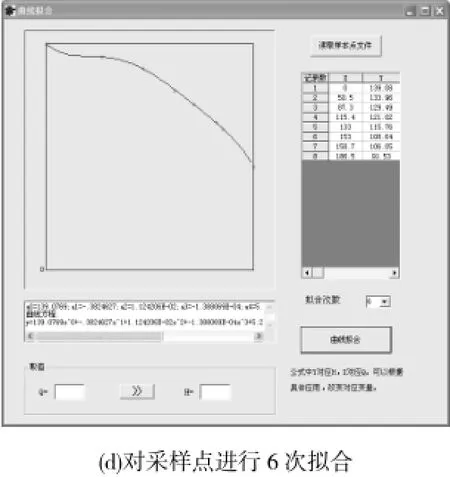
图1 拟合次数为3～6次后的程序界面Fig.1 Program interface fitted 3～6 times

2.1.2 去掉畸点拟合

去掉畸点3，再次对曲线进行拟合，重复上述步奏，可以看出曲线更加平滑且拟合次数直至7次，也没有发生病态(图2）。

图2 去掉畸点后拟合7次的程序界面Fig.2 The program interface fitted 7times after removing the abnormal point

最终所得7次方程为：

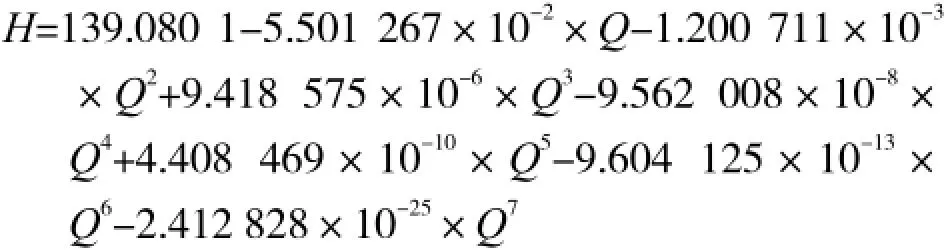
2.2 拟合值与测定值误差计算

对拟合后的H值与测定值进行比较计算，误差如表2。

综上，除去畸点3后，拟合曲线方程求解值与实测值误差全部在10的负4次幂以下，即便是畸点3验证后误差也仅为1.23×10-3，这说明本程序的求解值是较精确的。

表2 离心泵流量扬程采集值与拟合值误差表Table 2 Centrifugal pump Q - H acquisition and fitted values error table

3 结 语

通过上述基于VB 语言开发的程序，最终实现了最小二乘法拟合曲线这一复杂的数值计算以及绘图过程，轻松解出了离心泵流量和扬程曲线性能曲线的表达式。本程序具有如下优点:

（1）程序简单、易用、求解效率高；

（2）程序小巧、独立、占用内存小，对数据形式无特殊要求;

（3）程序适用范围广。由于本程序所采用的数学模型为多项式形式，所以本程序还可用于拟合各种容积泵的特性曲线方程，实际使用过程中只需要对变量进行相应的替换即可；

（4）拟合次数可由用户自选，人机交互界面友好;

（5）将拟合次数控制在多项式方程组多数良态以内，且拟合次数可由用户依据实际情况自选，拟合误差小，计算精度比较高。

［1］石一民. 离心泵性能曲线多项式拟合的一种简单方法[J]. 石油库与加油站, 2005, 14( 2): 40- 42.

［2］宋生奎，齐永生，等. 快速拟合离心泵性能曲线的两种方法[J] . 油气储运，2000，19 (7)：49-51: 57.

［3］商建平，俞树荣，等. 基于矩阵运算的离心泵性能曲线拟合方法[J].兰州石化职业技术学院学报, 2008, 8( 3)：14-15.

［4］陈乃祥，吴玉林. 离心泵[M]. 北京：机械工业出版社, 2003.

［5］魏佳广, 孙铁, 赵志海. 基于MATLAB GUI 技术的离心泵装置特性绘制软件二次开发[J]. 计算技术与自动化, 2010, 39(3)：27-30.

［6］王宏伟，王蕊，商德勇，于治福. 基于VB和Matlab混合编程的离心泵测试数据分析[J]. 煤矿机械, 2008, 29(5)：192-193.

［7］肖燕，孙崇浩，袁宗明，鞠兰. 离心泵流量-扬程性能曲线的拟合方法探讨[J]. 石油机械, 2006, 34（5）:68-69．

［8］宋岱才, 路永洁, 刘国志, 陈明明. 数值计算方法[M]. 北京：中国经济出版社，2006.

［9］李庆扬，王志超，易大义. 数值分析[M].第三版. 武汉：华中科技大学，1986.

［10］Burden，R.L. and Fairces J.D. Numerical Analysis Prindle[M]. Boston Weder Schmidt，1989.

Fitting Centrifugal Pump Performance Curve Based on Visual Basic

LIU Hong-ming1，SUN Tie1，LIU Song2，WANG Liang3，WEI Jia-guang4
（1. College of Mechanical Engineering，Liaoning Shihua University，Liaoning Fushun 113001，China；2. Engineering Training Center，Anyang Institute of Technology，Henan Anyang 455000，China；3. China Petroleum & Chemical Corporation Cangzhou Branch，Hebei Cangzhou 061000，China；4. COOEC Offshore Oil Engineering Co,.Ltd.，Tianjin 300452，China）

Centrifugal pump performance curve is the basis of measuring the performance, type selection calculation and optimal operation of the centrifugal pump. After the test，in order to get more accurate data based on the sampling point, curve of experimental data needs to be fitted. In this paper, taking fitting flow and head curve of centrifugal pump as an example, the method to fit the curve by programming based visual basic with the least square method was introduced. The practical application has proved that the method has many advantages, and can effectively solve data processing problems in centrifugal pump type selection and curve fitting in petrochemical industry.

Centrifugal pump；Performance curve；Least square method；Fitting curve；Visual Basic

TQ 018

： A

： 1671-0460（2014）04-0648-04

辽宁省教育厅科技基金项目，项目号：L2010250。

2013-10-10

刘红明（1986-），男，河北沧州人，硕士研究生，研究方向:离心泵及管路系统节能优化。E-mail：hope-victory@163.com。