Excel在非参数检验中的应用

2014-03-02何桂娟黄守婷杨建敏王景伟福建农林大学动物科学学院福州350002

福建畜牧兽医 2014年1期

关键词：参数检验秩次孵化率

何桂娟黄守婷杨建敏王景伟福建农林大学动物科学学院福州 350002

Excel在非参数检验中的应用

何桂娟黄守婷杨建敏王景伟福建农林大学动物科学学院福州 350002

本文以畜牧生产中两个具体实例，介绍了符号秩和检验法与Mann-Whitney秩和检验法的相关原理及利用Excel电子表格进行检验的计算方法和操作步骤。该方法具有直观、便捷和操作简单等特点，在实际畜牧生产中有较大的实用性。

Excel配对样本非配对样本秩和检验

在畜牧生产过程中，许多资料总体分布类型未知，且样本容量又较小，无法用参数统计法来解决，这时就可以采用非参数检验法（non-parametric test）。非参数检验在检验时不需利用总体参数（如平均数、标准差等）信息，主要利用样本数据之间的差值比较及大小顺序来检验数据资料是否来自同一个总体假设的检验方法，主要包括中位数检验、Wilcoxon符号秩和检验、Mann-Whitney秩和检验、Kruskal-Wallis检验等［1］。相对参数检验等方法，非参数检验对检验的限制较少，更能避免先见偏差；减少了应用中对假设条件的依赖，直观性强，易于接受［2］。

与大型专业统计软件如SAS和SPSS等相比较，Excel是一个统计功能丰富、操作方便、高效的统计软件。Excel在畜牧生产中已广泛运用于饲料配方优化计算，试验数据记录处理，绘制统计图等。利用Excel实现非参数检验，主要是利用其公式与函数等功能，逐一实现理论算法的每一步骤，具有操作简单，直观易懂等特点。因此，以畜牧生产中两个具体实例，介绍Excel的统计函数功能，实现样本资料的秩和检验，为解决生产实际问题提供参考。

1 利用Excel实现配对样本Wilcoxon符号秩和检验

1.1 配对样本 Wilcoxon符号秩和检验原理Wilcoxon符号秩和检验在符号检验法的基础上进一步考虑了差值绝对值的大小。绝对值的秩和能较明确地看出在数据的散布程度。设x1，x2，…xn，和y1，y2，…yn分别为来自总体X、Y的样本，X、Y的分布函数分别为连续函数F1（x）和F2（x），建立假设：

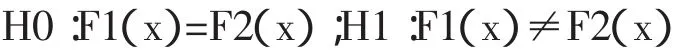
差值Zi=xi-y i（i=1，2，…n），取差值绝对值的秩，记为Ti。若Zi＞0，记其秩为Ti+，称为正秩，若Zi＜0，记其秩为Ti-，称为负秩。秩和绝对值较小者即为检验统计量T，再根据样本容量数查符号秩和检验表得5%水平的显著性临界T0.05，当检验统计量T小于该临界值时，就表明在这一显著水平下可以否定原假设［3］。

1.2 实例分析

1.2 .1 数据来源资料来源于某奶牛场利用两种方法检测10个奶样的乳脂率（%）（表1）。

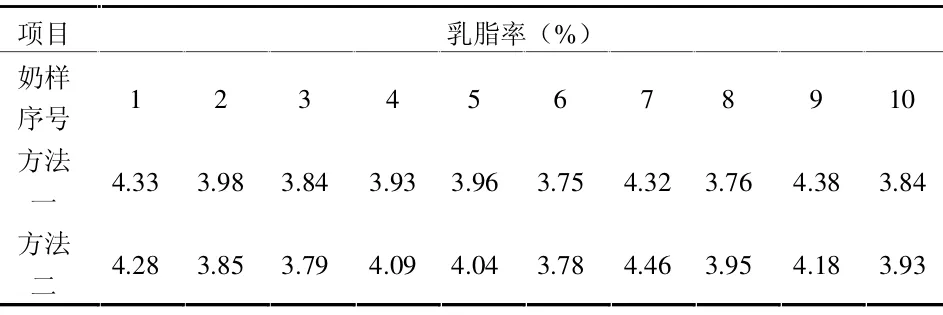
表1 两种方法检测的奶样乳脂率

1.2 .2 数据输入打开Excel工作表，将数据输入到电子表格（图1）。

1.2 .3 分析步骤根据输入数据计算两方法测定结果的差值，利用函数“ABS”得出各差值的绝对值，利用Excel排序功能，将绝对值的大小按从小到大顺序排列，每一差值绝对值对应的顺序号为该差值的秩次，若遇绝对值相同的情况则先求平均秩次，最后将秩次标上原差值符号，完成秩次的编辑（图1）。

点中G2单元的空白框后，在“公式”菜单栏中选择“插入函数”条目，点击“SUMIF”分析工具，弹出函数参数对话框（图2），点中表格秩次数据栏开始的F2单元，并拖动鼠标至F11单元，此时秩次数据自动进入变量区域，在“Criteria”选项中输入“＞0”的条件，点击“确定”按钮，即求得正秩次和T+，输入“＜0”的条件，则求得负秩次和T-（图1）。

图1 数据输入格式及秩次和计算结果

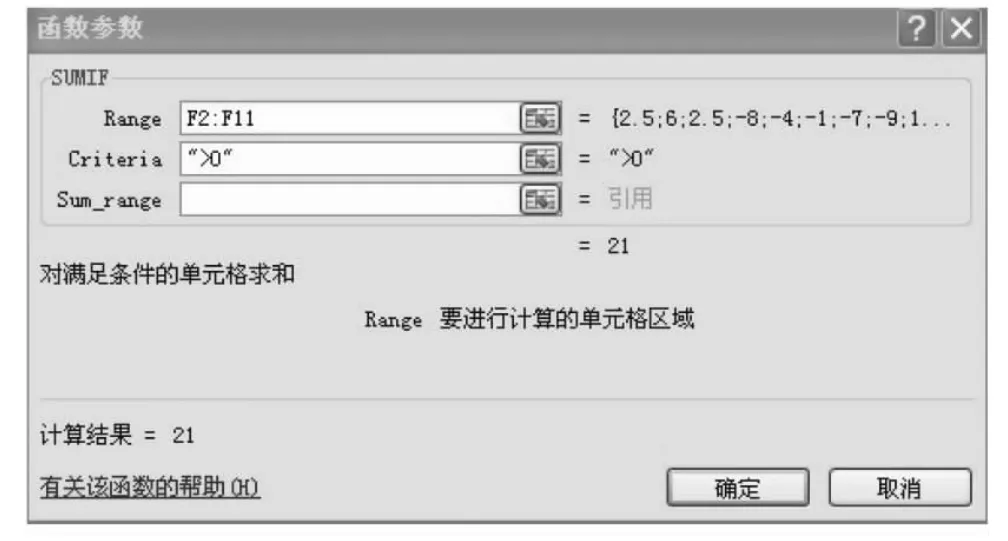
图2 条件求和参数对话框

1.2 .4 结果分析根据样本含量对子数n（n=10），查符号秩和检验表，得显著性水平为5%的临界值为T0.05（10）=8。由图1可知，秩和绝对值较小者为T+=21＞T，不能否定两种检测方法结果无差异的假设，表明两种检测方法结果在5%水平下差异不显著。

2 利用Excel实现独立样本符号秩和检验

2.1 独立样本符号秩和检验法独立样本秩和检验是抽自两个独立总体的两个独立样本之间的比较，该检验法又称为曼-惠特尼（Mann-Whitney）秩和检验。其基本原理是设两个总体X和Y，它们的分布函数分别为F1（x）和F2（x），建立假设：

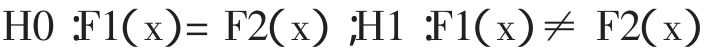
分别从这两个总体X、Y抽取容量为n1、n2的样本，n1+n2=n。计算取自总体X的样本秩次和为T1，取自Y的秩次和为T2，抽样较小的总体秩和即为检验统计量T值。如果两个总体的分布没有显著性差异，则T值不会太大或太小，而是靠近最大值和最小值的中间，于是可以将T值作为秩和检验的统计量，当T的实际值超过临界值时，就可以否定两总体的分布没有显著性差异的原假设［2］。

2.2 实例分析

2.2 .1 数据来源资料来源于某种禽公司孵化室对该公司2个养殖分场2012年1-8（9）月海兰蛋鸡的孵化率（表2）。

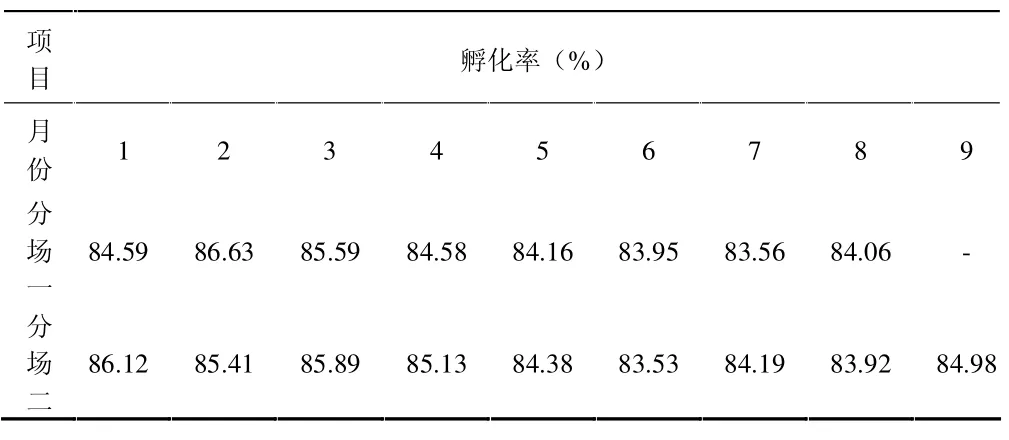
表2 海兰蛋鸡的孵化率

2.2 .2 数据输入打开Excel工作表，将数据输入到电子表格（编号1-8为分场一的孵化率，编号9-17为分场二的孵化率）（图3）。

2.2 .3 分析步骤将两组数据合并，按数值大小由小至大顺序排列，数值最小的秩次为1，数值最大的秩次为两组样本容量之和，相同数值计算平均秩次（图3）。点中D2单元区域的空白框，在“公式”菜单栏中选择“插入函数”条目，点击求和函数“SUM”，弹出求和函数参数对话框，点中电子表格该列数据开始的C2单元，并拖动鼠标至C9单元，此时秩次数据自动进入变量区域。点击“确定”按钮，即输出计算结果。用同样的方法求出分场二孵化率秩次和（图3）。

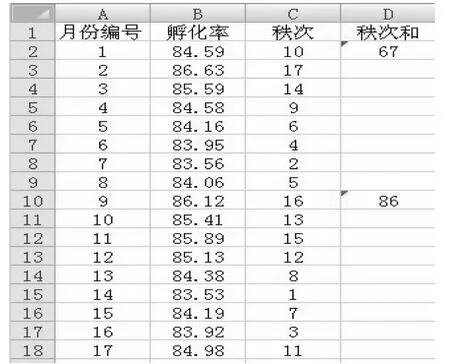
图3 数据输入格式及秩次和计算结果图

2.2 .4 结果分析根据样本含量令较小一组为n1，样本含量较大一组为n2，查非配对资料的秩和检验表可知，5%显著水平的上限与下限两个临界值T1= 54，T2=90。由图3可知，样本含量较小组的秩和T= 67＜T2，不能拒绝两总体分布没有显著性差异的原假设，即该公司两分场海兰蛋鸡孵化率在5%水平下差异不显著。