一类二部图生成的广义格子图的邻点可区别边染色
2014-03-02刘信生刘元元
刘信生,缑 艳,姚 兵,刘元元
(西北师范大学数学与统计学院,甘肃 兰州730070)
1 预备知识
图的染色问题是图论的重要研究内容之一,具有重要的理论价值和实际意义.由不同实际问题引出了不同的染色概念,如仓库数的研究、地图染色、有线通信网、无线通信网等引出的邻点可区别边染色问题,得到国内外图论研究者的关注.近些年来,虽然许多学者在这一领域已经取得了很多成果[1-8],但这方面的研究工作尚属开始,许多猜想的解决处于特殊图的验证阶段.本文定义了一类2维广义格子图H2(G,n,m;k1,k2),且通过从图的结构出发,利用构造染色的方法,得到了图H2(Kp,p,n,m;p,p)的邻点可区别边色数.从而验证了邻点可区别边色数猜想.
定义1[1]设G(V,E)是阶数至少为3的简单连通图,k-是正整数.若G(V,E)是一个k-正常边染色f 满足:∀uv∈E(G),S(u)≠S(v),其中S(u)={f(uv)|uv∈E(G)},则称f 为G 的一个k-邻点可区别边染色,简记为k-AVDPEC,且称χ′a(G)=min{k|G 存在k-AVDPEC}为G 的邻点可区别边色数.
猜想[1]设图G 是阶数至少为3的简单连通图,若G≠C5,则χ′a(G)≤Δ+2.
定义2 把一个根图G 做n 个拷贝,记做G(1),G(2),…,G(n).连接每相邻两个G(i)与G(i+1)(i=1,2,…,n-1)间的k1对顶点,所得的图记做H1(G,n;k1),并称为1 维广义格子图,见图1.然后把H1(G,n;k1)做m 个拷贝,记做H(1)1(G,n;k1),H(2)1(G,n;k1),…,H(m)1(G,n;k1).将H(j)1(G,n;k1)中的每个根图记为G(1,j),G(2,j),…,G(n,j)(j=1,2,…,m).连接G(i,j)与G(i,j+1)(i=1,2,…,n;j=1,2,…,m-1)间的k2对顶点,所得的图记做H2(G,n,m;k1,k2),并称为2维广义格子图,见图2.
注 定义2中的2维广义格子图不难推广到t维广义格子图Ht(G,n1,n2,…,nt;k1,k2,…,kt).

图1 1维广义格子图H1(G,n;k1)
引理1[1]对阶数不小于3的简单连通图G,有χ′a(G)≥Δ.若G 中存在相邻的最大度点,则

其他的相关术语和记号,可参见文献[9].

图2 2维广义格子图H2(G,n,m;k1,k2)
2 主要结果
定理1 对n≥3,m≥3,有χ′a(H2(Kp,p,n,m;p,p))=p+6.
证明 把根图Kp,p做n 个 拷 贝,记 做Kp(1,p),Kp(2,p),…,Kp(n,p).且 记V(Kp(i,)p)=Xi∪Yi,Xi∩Yi=∅,|Xi|=|Yi|=p,其 中Xi={v1(i),v2(i),…,vp(i)},Yi={u1(i),u2(i),…,up(i)}(i=1,2,…,n).连 接vj(i)与vj(i+1),uj(i)与uj(i+1)(i=1,2,…,n-1;j=1,2,…,p)后所得的图记做H1(Kp,p,n;p).然后把H1(Kp,p,n;p)做m 个拷贝,记做H1(1)(Kp,p,n;p),H1(2)(Kp,p,n;p),…,H1(m)(Kp,p,n;p).其中,H1(j)(Kp,p,n;p)中的每个根图记为Kp(1,p,j),Kp(2,p,j),…,Kp(n,p,j)(j=1,2,…,m).且 记V(Kp(i,,pj))=Xi,j∪Yi,j,Xi,j∩Yi,j=∅,|Xi,j|=|Yi,j|=p,其中Xi,j={v1(i,j),v2(i,j),…,vp(i,j)},Yi,j={u1(i,j),u2(i,j),…,up(i,j)}(i=1,2,…,n;j=1,2,…,m).连接vt(i,j)与vt(i,j+1),ut(i,j)与ut(i,j+1)(i=1,2,…,n;j=1,2,…,m-1;t=1,2,…,p)后所得到的图记做H2(Kp,p,n,m;p,p),见图3.

图3 2维广义格子图H2(Kp,p,n,m;p,p)
由于图H2(Kp,p,n,m;p,p)中存在相邻的最大度顶点,且Δ(H2(Kp,p,n,m;p,p))=p+4,由引理1可知,χ′a(H2(Kp,p,n,m;p,p))≥p+5,如果χ′a(H2(Kp,p,n,m;p,p))=p+5,那么不失一般性,可设(在这里,我们用(u)表示S(u)在颜色构成的集合{1,2,…,p+6}中的补集).那么点vt(i,j)的所有邻点的补集合里都必须包含色q.由于无论p是奇数还是偶数,由图H2(Kp,p,n,m;p,p)的结构可知,这些点中的任意两点之间都只有偶数条边相连,故不存在这p+4个点的完美匹配.因此,用p+5种颜色不能对图H2(Kp,p,n,m;p,p)进行邻点可区别边染色,故χ′a(H2(Kp,p,n,m;p,p))≥p+6,为证χ′a(H2(Kp,p,n,m;p,p))=p+6,只需给出H2(Kp,p,n,m;p,p)的一个p+6-AVDPEC即可.我们分两种情况来证明结论.
情况Ⅰ 当p≡1(mod 2)时,分以下四个步骤给出具体染色f:
ⅰ 对拷贝H1(1)(Kp,p,n;p)的边进行染色,令f 为:
当h≡1(mod 2)时,f(vi(h,1)uj(h,1))=[j+2(i-1)]p+2(i=1,2,…,p;j=1,2,…,p;h=1,2,…,n).
当h≡0(mod 2)时,f(vi(h,1)uj(h,1))=[j+2(j-1)]p+2(i=1,2,…,p;j=1,2,…,p;h=1,2,…,n).

ⅱ 对拷贝H1(2)(Kp,p,n;p)的边进行染色,令f 为:
当h≡1(mod 2)时,f(vi(h,1)uj(h,1))=[j+2(j-1)]p+2(i=1,2,…,p;j=1,2,…,p;h=1,2,…,n).
当h≡0(mod 2)时,f(vi(h,1)uj(h,1))=[j+2(i-1)]p+2(i=1,2,…,p;j=1,2,…,p;h=1,2,…,n).
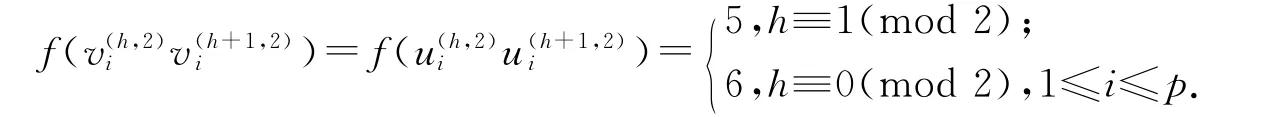
ⅲ 拷贝H(j)1(Kp,p,n;p)(j≡1(mod 2)且3≤j≤m)的边染色与H(1)1(Kp,p,n;p)的边染色完全一致,拷贝H(j)1(Kp,p,n;p)(j≡0(mod 2)且4≤j≤m)的边染色与H(2)1(Kp,p,n;p)的边染色完全一致.
ⅳ 对每相邻两个拷贝H(j)1(Kp,p,n;p)与H(j+1)1(Kp,p,n;p)(1≤j≤m-1)之间的边进行染色,令f 为:

下证明以上染色是邻点可区别的:
由图H2(Kp,p,n,,m;p,p)的结构可知,只需证明中的各顶点是邻点可区别的即可.因此,当i≡0(mod 2)且j≡0(mod 2)或当i≡1(mod 2)且j≡1(mod 2)时,对f 有当i≡0(mod 2)且j≡1(mod 2)或当i≡1(mod 2)且j≡0(mod 2)时,对f有
综上,易看出当p≡1(mod 2)时,图H2(Kp,p,n,m;p,p)中任意相邻两顶点的色集合均不同,故f是图H2(Kp,p,n,m;p,p)的一个p+6-AVDPEC.且满足邻点可区别边色数猜想.
情况Ⅱ 当p≡0(mod 2)时,分以下四个步骤给出具体染色f:
ⅰ 对拷贝H(1)1(Kp,p,n;p)的边进行染色,令f 为:



ⅱ 对拷贝H(2)1(Kp,p,n;p)的边进行染色,令f 为:


ⅲ 拷贝H(j)1(Kp,p,n;p)(j≡1(mod 2)且3≤j≤m)的边染色与H(1)1(Kp,p,n;p)的边染色完全一致,拷贝H(j)1(Kp,p,n;p)(j≡0(mod 2)且4≤j≤m)的边染色与H(2)1(Kp,p,n;p)的边染色完全一致.
ⅳ对每相邻两个拷贝H(j)1(Kp,p,n;p)与H(j+1)1(Kp,p,n;p)(1≤j≤m-1)之间的边进行染色,令f为:
下面证明以上染色是邻点可区别的:
由图H2(Kp,p,n,,m;p,p)的结构可知,只需证明中的各顶点是邻点可区别的即可.因此,当i≡0(mod 2)且j≡0(mod 2)或当i≡1(mod 2)且j≡1(mod 2)时,对f 有且且6≤t≤p.当i≡0(mod 2)且j≡1(mod 2)或当i≡1(mod 2)且j≡0(mod 2)时,对f 有且0(mod 2)且
综上,易看出当p≡0(mod 2)时,图H2(Kp,p,n,m;p,p)中任意相邻两顶点的色集合均不同,故f是图H2(Kp,p,n,m;p,p)的一个p+6-AVDPEC,且满足邻点可区别边色数猜想.
