考虑隐性故障时电网二级连锁过载的风险水平分析方法研究

邓慧琼，徐 刚，张 颖

（1.福建工程学院信息科学与工程学院，福建福州 350108；2.河北科技大学电气工程学院，河北石家庄 050018）

考虑隐性故障时电网二级连锁过载的风险水平分析方法研究

邓慧琼1，徐 刚2，张 颖2

（1.福建工程学院信息科学与工程学院，福建福州 350108；2.河北科技大学电气工程学院，河北石家庄 050018）

针对电网的二级连锁过载现象，并结合继电保护隐性故障，提出了一种风险水平研究方法：首先结合直流潮流法定义了二级连锁过载模式下的风险指标，然后从初始故障和剩余系统受扰支路的不同角度给出了3种进行风险水平统计的模型，进一步结合IEEE39节点系统，通过模拟计算对风险的统计结果及隐性故障中的参数对风险统计的影响进行了分析。所提出的方法可为分析具有不确定因素的电网连锁过载现象提供一定的借鉴。

电力系统；连锁故障；相继开断；隐性故障；统计规律

邓慧琼，徐 刚，张 颖.考虑隐性故障时电网二级连锁过载的风险水平分析方法研究［J］.河北科技大学学报，2014，35（2）：164-171.

DENG Huiqiong，XU Gang，ZHANG Ying.Research on risk level analysis method of cascading overload in power grid with two stages considering recessive faults［J］.Journal of Hebei University of Science and Technology，2014，35（2）：164-171.

电网连锁过载跳闸现象在大停电事故中经常出现，已经引起了越来越多的关注［1－4］，文献［5］研究了连锁过载深度发展所形成的多重故障的概率表示方法，文献［6］研究了基于潮流转移灵敏度的用于防止连锁过载的距离保护算法，文献［7］提出了基于地理信息系统的连锁过载分析算法并在实际电网中予以应用，文献［8］研究了基于广域信息的防止连锁过载跳闸的距离保护原理，等等。这些研究为进一步研究电网的连锁过载现象及其防治策略提供了很好的借鉴。

从当前的一些研究成果和已发生的停电事故来看，大规模的潮流转移和继电保护的隐性故障是引起电力系统连锁故障的重要因素［9－13］。由于隐性故障的存在，电网支路的连锁过载跳闸将呈现一定的不确定性，而采用确定性的分析方法将不利于把握这种不确定性，所以有必要建立针对这种不确定性的概率统计方法，以取得对隐性故障的进一步认识。就此，本文针对文献［14］中的一类继电保护隐性故障模型，定义了支路相继开断的风险统计指标，从统计初始故障支路和剩余系统支路的不同角度，给出了3种统计模型，并结合IEEE39节点系统进行了模拟计算，对隐性故障模型中各参数的影响作用进行了分析。

1 基本分析

由潮流转移引起的连锁过载事件本质上也是一种连锁故障，其一般表现为当电网中的某一支路发生初始故障后，该支路原来所传输的功率通过潮流转移分配到其他支路上去，如果某些支路发生过载时，这些支路就有可能跳闸。其跳闸的可能形式是：由于过载，线路的电气测量值进入某些III段保护的动作区内而被跳开；或被专门的过负荷保护跳开；或因其传输的功率超过了线路热稳定所允许的极限，致使导线软化进而与其下方的物体短路而被保护跳开。本文主要针对线路传输功率超过其热稳定极限的形式，并结合继电保护隐性故障对潮流转移产生的脆弱性问题进行分析，主要是针对初始故障支路开断到其引起潮流转移结束这一段场景展开研究，对于多级连锁过载，因为系统可能会出现复杂的动态行为，本文不考虑这种情况。

设电网的支路Lj发生了初始故障并被跳开，当潮流转移结束后，由直流潮流法可知，剩余系统中的支路Li的传输功率为［15］

式中：Pi（0）和Pj（0）分别为支路Li和Lj原来传输的功率；ΔPi（j）是支路Li的功率增量；λj（i）是支路Lj故障前支路Li的功率增量系数。

在考虑继电保护隐性故障时，支路Li的跳闸可能性可根据隐性故障的模型用概率来表示。对于继电保护的隐性故障模型，目前尚未有权威的统一标准，而且各种模型还需要实践的检验。对此，本文作如下考虑：1）任何符合实际的模型，其模型中的各种参数对电网的影响都需要进行研究考证；2）本文后面的算例需要结合一种模型进行模拟计算。所以本文暂采用文献［11］提出的隐性故障模型，并对该模型中的各个参数给出一个基本的分析。该模型目前在中国的文献中得到了较为普遍的采用，其具体形式如式（2）所示：

式中：Plimit为支路Li的允许潮流限值；Pi为支路Li的传输功率；PHF（i）为支路Li的动作概率；PM为继电保护正确动作概率；PH可看作是继电保护的基础隐性故障概率［9］。

对于式（2）所给出的模型，当Pi＞1.4Plimit时，PHF（i）是一个固定的正确动作率，以下主要针对前两种情况进行讨论。

1）当支路Li的Pi＜Plimit时，若Plimit值不变，PHF（i）与PH的变化呈线性关系；当PH值固定，随Plimit值的增加，PHF（i）保持等于PH值不变；当PH和Plimit值同时增加时，PHF（i）的变化主要受制于PH值的变化。

为了直观说明这种现象，在IEEE39节点系统通过模拟计算得到了1组结果，如图1所示。图中给出了某一初始开断故障发生后某一条满足Pi＜Plimit条件的支路其PHF（i）值随PH和Plimit变化的情况。其中，图1 a）给出的是固定Plimit值时PHF（i）值随PH值变化的曲线；图1 b）给出的是固定PH值时，PHF（i）值随Plimit值变化的曲线，可见其是一条水平的直线；图1 c）和图1 d）给出的是PH和Plimit从某一点开始同时增加时，PHF（i）值分别关于PH值和Plimit值的变化关系。由图1 c）可见，其变化关系和图1 a）的变化关系完全相同。由于这种情况下，Plimit值和PHF（i）值之间并无直接的代数关系，所以图1 d）所示出的关系是一种虚关系，结合图1 c）表明此种情况下PHF（i）值的变化主要决定于PH的值。

2）当支路Li满足Plimit＜Pi＜1.4Plimit的条件时，PHF（i）值与PH和Plimit值之间的关系略显复杂。类似地，为了直观地说明，图2示出了在IEEE39节点系统通过模拟计算得到的另一组结果。

图2 PH及Plimit取值与PHF（i）值之间的关系示例2Fig.2 Second example for the relationship between PHF and PH and Plimit

图2 a）给出的是固定Plimit值，且满足Plimit＜Pi＜1.4Plimit时PHF（i）值随PH值变化的曲线，显然该曲线呈线性变化趋势。图2 b）给出的是固定PH值时，PHF（i）值随Plimit变化的曲线，为了清晰显示，其Plimit的取值在一个较大的范围内滑动，f点和f＇点之间的一段是满足Plimit＜Pi＜1.4Plimit条件的曲线，可见随Plimit值的增加，PHF（i）值呈下降趋势。图2 c）是图2 a）和图2 b）的综合，其PH值的变化范围和图2 a）的相同，其Plimit值的变化范围和图2 b）的相同，图中g点和g＇点之间的一段是满足Plimit＜Pi＜1.4Plimit条件的曲线，其总体上呈下降的趋势。图2 c）中g点左边是满足Pi＞1.4Plimit条件的一段直线，PHF（i）的值由PM值决定；其g＇点右边是满足Pi＜Plimit的一段曲线，此时其表现和图1 c）完全类似。图2 c）表明Plimit的变化会给PHF（i）的变化带来转折效应，只要Plimit的取值能够在Pi＜Plimit，Plimit＜Pi＜1.4Plimit和Pi＞1.4Plimit这3种条件范围内滑动，图2 c）中以g点和g＇点为转折点的3段曲线必定会出现。而PH的作用则不同，除Pi＞1.4Plimit条件外，在其他2种条件下，其值的增加均会使PHF（i）出现增加的趋势，具有连续的刚性特征。图2 c）中从g点到g＇点之间的这一段曲线在总体上一定会呈下降趋势，但在这段曲线的局部也可能会出现波动，随着PH和Plimit值的增大，PHF（i）局部值的增减主要决定于其对PH和Plimit各自的灵敏度以及PH和Plimit各自的增加方式。为了说明这种情况，图2 d）给出了图2 c）中g和g＇两点间某一段与图2 c）不同的PH和Plimit增加方式，可见，PHF（i）出现了明显的波动，这也说明即便增加Plimit的值，但如果其增加值不适当的话，也会出现PHF（i）值较高的情况。

以上的讨论只限于针对某一特定的初始开断故障对电网其余部分的单一支路的影响而言，当样本数量增加时，在统计意义下，其情况究竟如何需要进一步研究。

2 统计模型及仿真分析

当支路Li发生连锁开断后，支路Li所传输的功率Pi将进一步在电网中扩散，所以可以采用如下的指标来表示支路Li开断后的风险：

下面分3种情况分别定义均值、样本差和统计离散度等指标，并给出分析方法。

1）某一支路Li在其他任一支路Lj分别作为初始开断支路情况下的统计表现。其风险的均值、样本差和统计离散度分别定义为

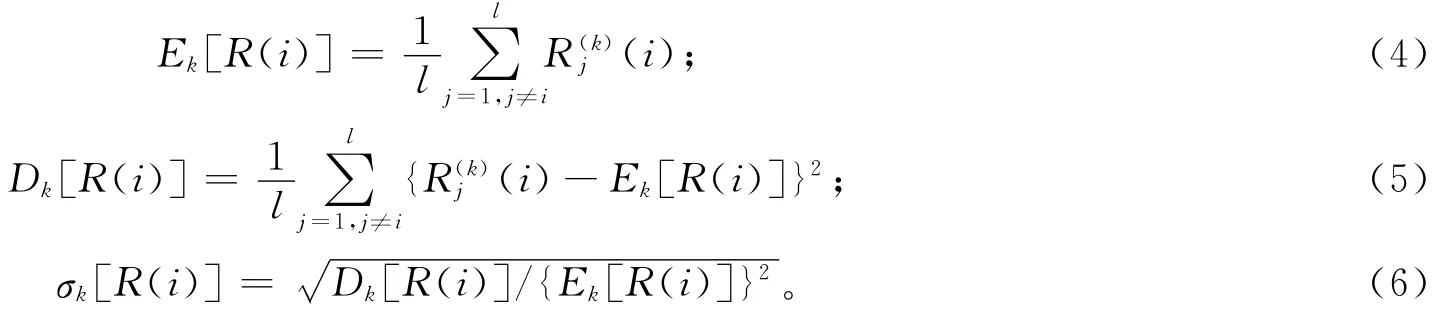
式（4）、式（5）中l为待考察初始故障支路总数；k表示第k次改变PH或Plimit的值进行模拟计算。

图3示出了按上述原则在IEEE39节点系统计算后的几组典型结果。其中图3 a）示出的是固定Plimit值得到的2组计算结果；图3 b）示出的是固定PH值得到的2组计算结果。图中，为了将所有的参量变化曲线示于同一图上，部分参量按一定比例作了缩放，以下其他图中也按类似办法处理。

由图3可见其风险的均值、样本差和统计离散度的总体变化情况以及隐性故障中各参数对其的影响。

图3 统计分析算例1Fig.3 First example for statistic analysis

图3 a）中画出的2组曲线，一组是被考察的支路在任何其他支路作为初始开断支路的情况下都满足Pi＜Plimit，这一组曲线如图中E1，D1和σ1所示，此时，PHF（i）完全由PH决定，故而，其E值呈线性增长趋势，D值按平方趋势增长，而σ表现为水平直线，表明D值开方后和E值的增长趋势完全一致。另一组是被考察的支路在任何其他支路作为初始开断支路的情况下，有一部分满足Plimit＜Pi＜1.4Plimit的条件，这一组曲线如图中E2，D2和σ2所示，由图可见，此时，其E值随PH值的增加仍呈线性增长趋势，而D值和σ值均呈下降趋势，这种情况说明随着PH值的增加，支路被连锁开断的风险向着一个较高的平均水平集中，这种情形是较为危险的。另外，对于被考察的支路在任何其他支路作为初始开断支路的情况下均满足Pi＞1.4Plimit条件的情形，图中未予画出，在此种情形中，E值、D值和σ值不随PH值而变化，反映在图中则为3条水平直线，因为此时的支路开断风险决定于PM值。

图3 b）中画出的2组曲线，一组是被考察的支路在任何其他支路作为初始开断支路的情况下其功率波动较大的情形，如图中E3，D3和σ3所示。另一组是被考察的支路在任何其他支路作为初始开断支路的情况下其功率波动较大的情形，如图中E4，D4和σ4所示。在计算时，让Plimit的值在一个较大的范围内变化（实际中某些较小的或较大的Plimit取值可能不会出现，此处主要是为了完整地展示Plimit的作用，以下其余的算例分析也按此处理）。由图可见，这两组的E值随Plimit值的变化，出现明显的分段转折现象，其中的2条水平直线分别满足Pi＞1.4Plimit和Pi＜Plimit条件，其支路开断的风险由PM值和固定的PH值决定，另外的一条呈下降趋势的曲线则是Plimit＜Pi＜1.4Plimit的条件。这和前述单一初始开断的情形十分相似，说明随着Plimit值增加支路连锁开断的风险水平将会下降。这两组结果的主要差别在于其D值和σ值，其中D4和σ4的变化趋势基本相似，经分析发现，该被考察支路在其他支路初始开断的情况下其功率值波动很小。而D3和σ3的变化趋势相比有较大的波动，经分析发现，该被考察支路在其他支路初始开断的情况下其功率值波动很大，如图4所示。

图4 支路功率波动较大示例Fig.4 An example for larger power fluctuation of a certain branch

2）任一支路Lj开断后，其在其他支路上所引起的风险统计表现，即其风险的均值、样本差和统计离散度分别定义为

式（7）、式（8）中l为待考察的剩余系统支路总数；其余变量的定义同前。按上述原则，图5示出了在IEEE39节点系统计算后的几组典型结果。其中图5 a）示出的是固定Plimit值得到的2组计算结果；图5 b）示出的是固定PH值得到的一组计算结果。

图5 a）中画出的2组曲线，一组是被考察的支路在任何其他支路作为初始开断支路的情况下都满足Pi＜Plimit，如图中的E1，D1和σ1所示。另一组示出的是部分支路满足Plimit＜Pi＜1.4Plimit的条件的情形，如图中的E2，D2和σ2所示。这两组的表现和图3 a）中的表现完全相似，另外，对于支路功率均满足Pi＞1.4Plimit条件的情形，图中未予画出，此时的支路连锁开断的风险决定于PM值，其E值、D值和σ值在图中表现为水平直线。

图5 b）的一组曲线，其表现和图4 b）中的第2组曲线的表现基本类似，随着全部支路从满足Pi＞1.4Plimit的条件，然后逐渐到有部分支路满足Plimit＜Pi＜1.4Plimit的条件，直至所有支路Pi＜Plimit的条件，其E值的变化呈分段转折变化，不过其转折点较为光滑，这是因为在转折处只有部分支路满足下一段的要求，这同时也影响到了D值和σ值的表现，如图所示，D值和σ值有较大的波动，这说明在不同条件之间的过渡阶段，不同支路的开断风险表现出较大的差异。

图5 统计分析算例2Fig.5 Second example for statistic analysis

3）综合考虑所有的初始故障和每一初始故障作用后的剩余系统支路的表现，其风险的均值、样本差和统计离散度分别定义为

式（10）、式（11）中l1和l2分别为待考察的初始故障支路总数和每一初始故障发生后待考察的剩余系统支路总数；其余变量的定义同前。按上述原则，图6示出了在IEEE39节点系统计算后结果。其中图6 a）示出的是固定Plimit值得到的一组计算结果；图6 b）示出的是固定PH值得到的一组计算结果。

图6 统计分析算例3Fig.6 Third example for statistic analysis

在固定Plimit值时，PH值对连锁开断风险的影响与图5 a）中的完全相似，图6 a）只画出了有部分支路满足Plimit＜Pi＜1.4Plimit条件的情形，由图可见，其E值随PH值的增加而增加。图6 a）中示出的D值是增加的情形，实际上D值也可能随PH值的增加而减小，这与Plimit值有关，若逐渐减小Plimit的值，随着满足Plimit＜Pi＜1.4Plimit条件的支路数量的增多，D值会逐渐由上升变为下降。但不论D值增减，计算表明σ值均呈下降或水平趋势，这说明在这一阶段，随着E值的增加，各支路的连锁开断风险的差异逐渐被掩盖了。

图6 b）的一组曲线和图5 b）的一组曲线基本相似，显示了Plimit的分段转折效应。

综合以上可见，在统计意义上，在Pi＜1.4Plimit的范围内，PH值的增大会导致支路连锁开断风险的平均水平持续增加，具有刚性特征；而Plimit的表现为若其在较大范围内变动时，对支路连锁开断风险平均水平的影响具有分段转折效应，并会造成较强的波动。为了进一步说明这些基本特征，图7示出了在IEEE39节点系统上同时增大PH值并减少Plimit值且按式（10）、式（11）和式（12）进行计算的另一组结果。

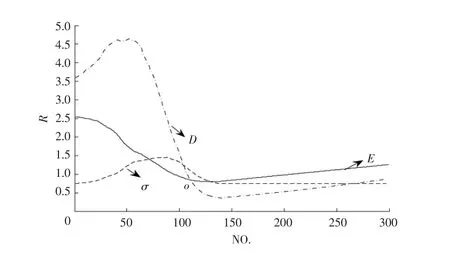
图7 统计分析算例4Fig.7 Fourth example for statistic analysis

由图7可见，随着Plimit值在较大范围内的变化，其支路连锁开断风险的平均水平的变化趋势及D值和σ值的变化情况与图6 b）的情况基本一致，只是随着Plimit值的增大，其E值主要决定于PH值，如图中o点右边的一段曲线所示。

3 结 语

针对继电保护隐性故障模型，将R（i）定义为支路相继开断的风险统计指标，对IEEE39节点系统进行模拟计算，结合了初始故障支路、剩余系统支路及两者相结合的角度，得到了3种统计模型，初步得到部分结论。支路的传输功率的增大会刚性地导致支路连锁开断风险的平均水平持续增加；支路的允许潮流极限值的变化，会受到各个支路对系统的敏感程度不同而表现出分段效应，支路连锁开断风险显示出波动结果；系统产生连锁开断的风险主要由支路传输功率决定。由潮流转移引起的电网连锁性支路相继开断现象，在考虑继电保护隐性故障时，由于受到较多因素及其相互耦合作用，其表现行为比较复杂，需要建立一些统计方法对其进行研究，这样可对其中隐性故障的影响因素以及电网在统计意义下的风险水平有一个比较清晰的把握。

［1］ 袁季修.防御大停电的广域保护盒紧急控制［M］.北京：中国电力出版社，2007.

YUAN Jixiu.Wide Area Protection and Emergency Control to Prevent Large Scale Blackout［M］.Beijing：China Electric Power Press，2007.

［2］ 邓慧琼，王 帅，孙克军，等.一种考虑二级连锁过载的电网故障关联区域划分方法［J］.河北科技大学学报，2012，33（3）：237-243.

DENG Huiqiong，WANG Shuai，SUN Kejun，et al.Consider a secondary chain overload of power grid failure correlation region partition method［J］.Journal of Hebei University of Science and Technology，2012，33（3）：237-243.

［3］ 邓慧琼，苏爱宁，孙克军.考虑潮流水平变化的电网二级连锁过载中的涨落现象研究［J］.河北科技大学学报，2012，33（4）：313-318.

DENG Huiqiong，SU Aining，SUN Kejun.Research on fluctuation phenomenon of cascading overload with two stages in power network considering power flow level［J］.Journal of Hebei University of Science and Technology，2012，33（4）：313-318.

［4］ 陈哲星，宋 玮，董 卓，等 电网故障序列预测［J］.河北工业科技，2010，27（6）：471-472.

CHEN Zhexing，SONG Wei，DONG Zhuo，et al.Fault sequence forecast of power grid［J］.Hebei Journal of Industrial Science and Technology，2010，27（6）：471-472.

［5］ 韩学军，石 磊，朱 岩，等.考虑多重故障的连锁过载分析［J］.电网技术，2008，32（16）：86-89.

HAN Xuejun，SHI Lei，ZHU Yan，et al.Analysis on cascading overload considering multiple failures［J］.Power System Technology，2008，32（16）：86-89.

［6］ 张亚迪，陈柏超，邢海英，等.基于转移潮流反应灵敏度的新型距离保护算法［J］.电力自动化设备，2008，28（11）：35-39.

ZHANG Yadi，CHEN Baichao，XING Haiying，et al.Algorithm of distance protection based on transfer power flow sensibility［J］.Electric Power Automation Equipment，2008，28（11）：35-39.

［7］ 闫丽梅，赵国成，陈 娟，等.基于GIS的大庆油田电力系统连锁过负荷故障分析系统［J］.电力系统保护与控制，2010，38（23）：75-81.

YAN Limei，ZHAO Guocheng，CHEN Juan，et al.GIS based overload cascading failure analysis system in Daqing oil-field power system［J］.Power System Protection and Control，2010，38（23）：75-81.

［8］ 王 艳，张艳霞，徐松晓.基于广域信息的防连锁过载跳闸保护［J］.电力系统自动化，2008，32（10）：37-41.

WANG Yan，ZHANG Yanxia，XU Songxiao.A protection scheme against chain over-load trip based on wide-area information［J］.Automation of Electric Power Systems，2008，32（10）：37-41.

［9］ 杨明玉，田 浩，姚万业.基于继电保护隐性故障的电力系统连锁故障分析［J］.电力系统保护与控制，2010，38（9）：1-5.

YANG Mingyu，TIAN Hao，YAO Wanye.Analysis of power system cascading failure based on hidden failures of protective relaying［J］.Power System Protection and Control，2010，38（9）：1-5.

［10］ 邓慧琼，李 争，孙丽华，等.电网连锁故障的激发因素研究［J］.河北科技大学学报，2010，31（3）：222-226.

DENG Huiqiong，LI Zheng，SUN Lihua，et al.Research in triggering factors of power network cascading failure［J］.Journal of Hebei University of Science and Technology，2010，31（3）：222-226.

［11］ 边肇祺，张学工.模式识别［M］.北京：清华大学出版社，2000.

BIAN Zhaoqi，ZHANG Xuegong.Pattern Recognition［M］.Beijing：Tsinghua University Press，2000.

［12］ 范九伦，吴成茂，丁 夷.基于样本最大分类信息的聚类有效性函数［J］.模糊系统与数学，2001，15（3）：68-73.

FAN Jiulun，WU Chengmao，DING Yi.A cluster validity function based on maximum classification information［J］.Fuzzy Systems and Mathematics，2001，15（3）：68-73.

［13］ 沈晓凡，舒治淮，吕鹏飞，等.2006年国家电网公司继电保护装置运行情况［J］.电网技术，2008，32（3）：18-21.

SHEN Xiaofan，SHU Zhihuai，LYU Pengfei，et al.Operation situation of protective relayings of state grid corporation of China in 2006［J］.Power System Technology，2008，32（3）：18-21.

［14］ CHEN J，THORP J S，DOBSON I.Cascading dynamics and mitigation assessment in power system disturbances via a hidden failure model［J］.Electrical Power and Energy Systems，2005，27（4）：318-326.

［15］ 吴际舜.电力系统静态安全分析［M］.上海：上海交通大学出版社，1985.

WU Jishun.Power System Static Security Analysis［M］.Shanghai：Shanghai Jiaotong University Press，1985.

Research on risk level analysis method of cascading overload in power grid with two stages considering recessive faults

DENG Huiqiong1，XU Gang2，ZHANG Ying2
（1.School of Information Science and Engineering，Fujian University of Technology，Fuzhou Fujian 350108，China；2.School of Electrical Engineering，Hebei University of Science and Technology，Shijiazhuang Hebei 050018，China）

In order to solve the two-stage cascading overload problem considering the hidden failure in relay protection，a risk level research method is presented.Firstly，using the DC power flow method to define the risk indicators in the two-stage cascading overload mode，and three statistical risk models from different angles for the initial fault system and the remaining failure branches in power network are proposed.Then，integrated with the IEEE39 node system，the effects of the statistical results and risk parameters in hidden failures on the risk statistics are analyzed by simulation.The proposed method can provide a reference for the analysis of power grid cascading overload phenomenon with uncertainties.

power system；cascading failure；successive failure；hidden failure of relay；statistical rule

TM711

A

1008-1542（2014）02-0164-08

10.7535／hbkd.2013yx06009

2013-04-24；

2014-02-23；责任编辑：李 穆

福建省教育厅基金（JB13143）；福建工程学院科研项目（GY-Z13104）

邓慧琼（1972-），男，山西大同人，副教授，博士，主要从事电网连锁故障分析方面的研究。

E-mail：denghuiqiong72＠126.com