基于均值迁移的粒子滤波算法研究

黄莉静，于乃文，王敬涛

（1.河北科技大学信息科学与工程学院，河北石家庄 050018；2.河北科技大学理工学院，河北石家庄 050018；3.石家庄学院计算机系，河北石家庄 050035）

基于均值迁移的粒子滤波算法研究

黄莉静1，于乃文2，王敬涛3

（1.河北科技大学信息科学与工程学院，河北石家庄 050018；2.河北科技大学理工学院，河北石家庄 050018；3.石家庄学院计算机系，河北石家庄 050035）

针对弱观测噪声环境下的粒子退化现象，特别是观测噪声较小时非线性非高斯的粒子滤波问题，提出了一种基于均值迁移的粒子滤波算法。首先，将核密度估计的无参快速模式匹配算法引入到粒子滤波中，并迭代计算概率密度估计。然后，利用均值迁移估计粒子梯度的方向，计算每个粒子移向其样本的均值。当粒子位置发生改变时，对重采样粒子进行加权处理。最后，根据本算法采样更新粒子集，有效地克服了粒子退化现象并提高了状态估计精度。

后验分布；密度估计；均值迁移；加权值；粒子滤波

黄莉静，于乃文，王敬涛.基于均值迁移的粒子滤波算法研究［J］.河北科技大学学报，2014，35（2）：184-188.

HUANG Lijing，YU Naiwen，WANG Jingtao.Particle filter algorithm based on mean-shift［J］.Journal of Hebei University of Science and Technology，2014，35（2）：184-188.

粒子滤波是一种基于蒙特卡洛方法和递推贝叶斯估计的统计滤波方法［1－3］，根据大数定理采用蒙特卡洛的方法来求解贝叶斯估计中的积分运算，国内外已经取得了一定的进展。文献［4］提出了似然粒子滤波（LPF），它使用似然函数作为建议分布，考虑了最新观测信息，而且保证大部分的粒子位于高似然区，从而提高了粒子的利用效率，使得状态估计更加准确。文献［5］利用卡尔曼粒子滤波来产生建议分布。文献［6］提出自适应粒子群优化的新型粒子滤波算法，该方法实现简单，但是对于最新粒子的观测值却容易偏离真实的后验概率。上述文献中的粒子滤波均存在一个主要问题是粒子的退化现象，尤其是当观测噪声较小并且似然粒子滤波形状尖锐时，粒子的退化现象比较严重。

针对粒子退化现象的常用解决方法是对粒子进行重采样，但是经过重采样之后，权值大的粒子会被多次复制，导致粒子集失去多样性，出现样本枯竭现象。针对这一问题文献［7］提出高斯粒子滤波算法，利用高斯分布近似于状态后验概率密度这一特点进行高斯化的粒子滤波，当高斯假设成立时该算法是渐进的最优。文献［8］提出了粒子滤波与均值漂移相结合的算法，该算法从后验分布的连续近似中重采样来更新粒子集，从而增加粒子的多样性。文献［9］在似然粒子滤波的基础上提出了正则似然粒子滤波（R-LPF）算法，通过构建状态的连续后验概率密度来获得新的样本粒子。

本研究针对弱观测噪声条件下的非线性非高斯的动态系统的滤波问题，提出了基于加权均值迁移的粒子滤波算法。该算法首先将核K－密度估计的无参快速模式匹配算法引入到粒子滤波中，并迭代计算概率密度估计。然后利用均值迁移估计粒子梯度的方向，计算每个粒子移向其样本的均值，当粒子位置发生改变时，对粒子采样进行加权处理。实验证明了本算法的可行性和有效性。

1 传统粒子滤波算法

1.1 重要密度函数

1.2 粒子滤波算法

粒子滤波算法选择最易于实现的先验概率密度作为重要密度函数，即

将式（7）代入到式（6），则可将重要性权值可简化为

将权值做归一化处理可得

则后验概率密度可表示为

当Ns→＋∞，有大数定理可以保证式（10）的后验概率密度逼近与真实的后验概率密度p（xk｜z1：k）。

综上所述，粒子滤波算法表述如下。

1）粒子初始化：有先验概率p（x0）产生粒子群集，所有粒子权值为

2）权值更新：在时刻k，对粒子权值进行更新，更新结果为

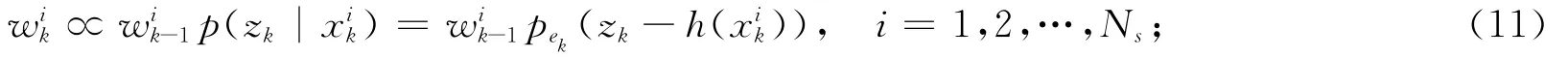
3）重采样：重新得到新的粒子集合｛xi＊0：k，i＝0，1，2，…，Ns｝；

4）结果输出：在时刻k，未知参数x的最小均方估计为

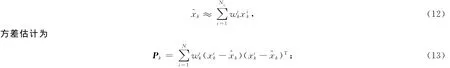
5）状态预测：利用方程预测未知参数xik＋1；

6）在下一个时刻k＝k＋1时，转到第2）步循环执行，直到结束为止。

2 对传统粒子滤波算法分析

当重要性函数近似接近于后验概率分布时，则可以用重要性函数代替后验概率分布作为采样函数，但是此时要求重要性函数的方差基本为0，即

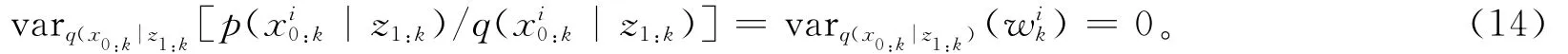
由于传统的粒子滤波算法选择先验概率作为重要性密度函数，如果是在量测精度要求低的场合，这种选取方法能够获得较好的结果。但是对于量测精度要求高的场合，由于在进行更新时没有考虑当前观测值，使得从重要性概率密度中取样得到的样本与从真实后验概率密度采样得到的样本有较大偏差，尤其是当似然函数位于系统状态转移概率密度的尾部或似然函数程尖峰状态时，这种偏差更加明显。

3 均值迁移粒子滤波算法

3.1 核K－ 密度估计

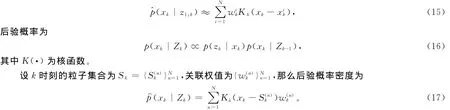
3.2 加权粒子均值迁移

本研究的均值迁移是将核K－密度估计的无参快速模式匹配算法，引入到粒子滤波中的一种迭代计算概率密度估计的方法。

利用均值迁移估计粒子梯度的方向，通过式（18）计算每个粒子移向其样本的均值：

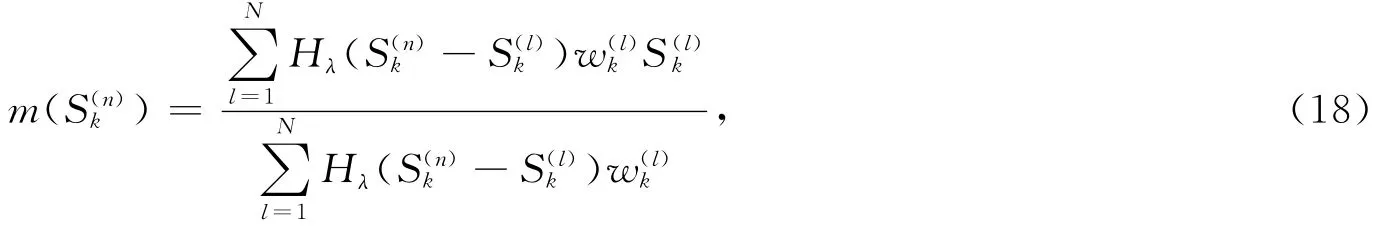
其中H是任意的核K值。

在均值迁移算法中，需要对每个粒子重复使用，但是当粒子位置发生改变时，新采样粒子并不流向后验分布，因此本研究对粒子采用加权处理的方法。

设在k时刻粒子第i次均值迁移后的粒子集合为｛S（n）k，i｝，利用式（19）中的粒子概率密度平衡系数估算新粒子位置：

4 实验仿真

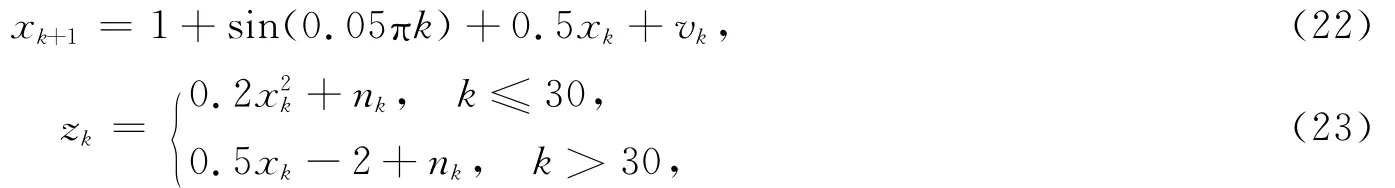
其中：vk为系统过程噪声，服从Gamma分布；nk为弱观测噪声。

为了验证算法的有效性和准确性，实验选取具有代表性的标准测试视频序列进行实验验证。实验平台为Pentium 4，2.53 GHz的CPU，2GB内存的PC机，编程环境是采用Matlab R2009a实现，粒子数为60。

本研究实验分别使用传统粒子滤波（PF）、似然粒子滤波（LPF）、正则似然粒子滤波（R-LPF）以及本研究提到的加权均值迁移粒子滤波4种粒子滤波算法进行比较实验中迭代步长为T＝60。重采样阈值为Nth＝N／5。

由图1可以看出，本研究算法的估计效果优于标准粒子滤波，更接近于实际状态值。

为了更进一步的验证本研究算法的有效性，进行100次蒙特卡罗仿真实验，对各种算法计算粒子状态的

本研究以弱观测动态模型作为实验对象，系统状态转移方程和观测方程为均方根误差（RMSE），图2中所示为各个算法的均方根误差的曲线图。

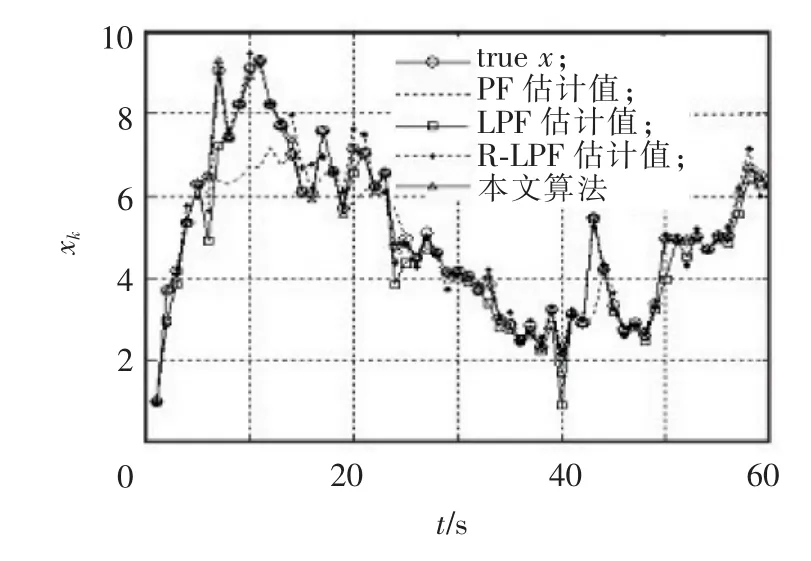
图1 不同算法状态估计值Fig.1 State estimation of different algorithm

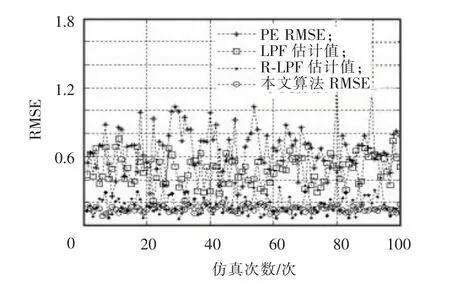
图2 不同算法的RMSEFig.2 RMSE of different algorithm

不同算法估计结果的RMSE均值、方差及各算法平均运行时间如表1所示。

由表1可以看出，本研究算法的均方根误差和方差较其他3种算法更小，经过图2的100次仿真得到的很小的RMSE均值也验证了本文算法的收敛性，运行时间与R-LPF算法相比时间复杂度更低。

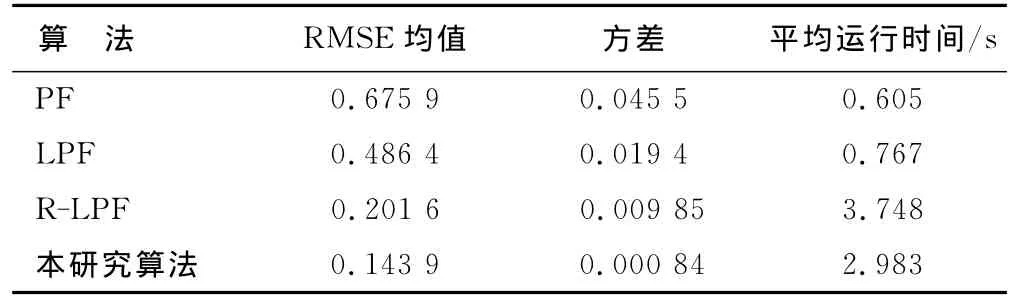
表1 不同算法的状态估计比较结果Tab.1 State estimation comparison results

5 结 语

本研究针对弱观测噪声条件下的非线性非高斯的动态系统的滤波问题，提出了基于加权均值迁移的粒子滤波算法。本研究算法相对于其他算法优越之处在于算法中涉及的所有粒子均参与了任意时刻的粒子更新，每一个粒子都进行均值迁移和加权后的粒子概率密度平衡系数估算新粒子位置，使得粒子集中包含了更多相异的粒子路径，从而改善了粒子集的多样性。

［1］ 刘曙光，刘明远，何 钺.机器视觉及其应用［J］.河北科技大学学报，2000，21（4）：11-15.

LIU Shuguang，LIU Mingyuan，HE Yue.The machine vision and its application［J］.Journal of Hebei University of Science and Technology，2000，21（4）：11-15.

［2］ 李 科，徐克虎，黄大山.改进的均值漂移和粒子滤波混合跟踪方法［J］.计算机应用，2012，32（2）：504-506.

LI Ke，XU Kehu，HUANG Dashan.Improved object tracking method based on mean shift and particle filter［J］.Journal of Computer Applications，2012，32（2）：504-506.

［3］ HU X L，SCHON T B，LJUNG L.A basic convergence result for particle filtering［J］.Signal Processing，2008，56（4）：1337-1348.

［4］ ARULAMPALAM M S，MASKELL S，GORDON N，et al.A tutorial on particle filters for online nonlinear／non-Gaussian Bayesian tracking［J］.Signal Processing，2002，50（2）：174-188.

［5］ 夏 楠，邱天爽，李景春，等.一种卡尔曼滤波与粒子滤波相结合的非线性滤波算法［J］.电子学报，2013，41（1）：148-152.

XIA Nan，QIU Tianshuang，LI Jingchun，et al.A nonlinear fitering algorithm combining the Kalman filter and the particle filter［J］.Acta Electronica Sinica，2013，41（1）：148-152.

［6］ 陈志敏，薄煜明，吴盘龙，等.基于自适应粒子群优化的新型粒子滤波在目标跟踪中的应用［J］.控制与决策，2013，28（2）：193-200.

CHEN Zhimin，BO Yuming，WU Panlong，et al.Novel particle filter algorithm based on adaptive particle swarm optimization and its application to radar target tracking［J］.Control and Decision，2013，28（2）：193-200.

［7］ SHAN Caifeng，WEI Yucheng，TAN Tieniu，et al.Real time hand tracking by combining particle filtering and mean-shift［A］.Sixth IEEE International Conference on Automatic Face and Gesture Recognition［C］.Seoul：IEEE Computer Society，2004.669-674.

［8］ 韩 明，刘教民，王震洲，等.适用于多目标跟踪的 MSPF算法研究［J］.河北工业大学学报，2012，41（5）：15-19.

HAN Ming，LIU Jiaomin，WANG Zhenzhou，et al.Research on MSPF algorithm for multi-target tracking［J］.Journal of Hebei University of Technology，2012，41（5）：15-19.

［9］ JULIER S J，UHLMANN J K，DURRAN W H F.A new method for nonlinear transformation of means and covariances in filters and estimators［J］.IEEE Trans Automatic Control，2000，45：477-482.

Particle filter algorithm based on mean-shift

HUANG Lijing1，YU Naiwen2，WANG Jingtao3
（1.School of Information Science and Engineering，Hebei University of Science and Technology，Shijiazhuang Hebei 050018，China；2.Polytechnic College，Hebei University of Science and Technology，Shijiazhuang Hebei 050018，China；3.Department of Computer Science，Shijiazhuang University，Shijiazhuang Hebei 050035，China）

To cope with particle degeneracy with weak measurement noise，especially the particle filter problems of nonlinear／non-Gaussian when the measurement noise is smaller，a particle filter algorithm is proposed based on mean-shift.Firstly，non-parametric fast pattern matching algorithm of Kernel density estimation is introduced for particle filter，and the probability density estimation is iteratively calculated.Then，particle gradient direction and the mean value for each particle that moves to the sample are estimated by mean shift.When the position of particles is changed，the re-sampled particles are weightily processed.Finally，using the method to update particle sets overcomes the particle degradation effectively and improves the accuracy of state estimation.

posterior distribution；density estimation；mean-shift；weighted value；particle filter

TP391

A

1008-1542（2014）02-0184-05

10.7535／hbkd.2014yx02013

2013-09-12；

2013-11-03；责任编辑：张 军

河北省自然科学基金（F2012208004）；河北省科技支撑计划项目（12210807）

黄莉静（1977-），女，河北张家口人，硕士，主要从事网络与数据库、数据挖掘方面的研究。

E-mail：rnhlj＠hebust.edu.cn