均值分组块补零P码直捕算法原理及实现

于国庆，靳 蕊，李永伟

（1.河北科技大学信息科学与工程学院，河北石家庄 050018；2.河北科技大学电气工程学院，河北石家庄 050018）

均值分组块补零P码直捕算法原理及实现

于国庆1，靳 蕊1，李永伟2

（1.河北科技大学信息科学与工程学院，河北石家庄 050018；2.河北科技大学电气工程学院，河北石家庄 050018）

P码是长周期精密测距码，主要用于提供精确定位服务。提出了基于FFT的均值分组块补零P码直捕算法，通过直接平均法来降低运算量，用分段重叠补零法将连续的相干积分分解成普通的循环相关，对接收码和本地码的FFT结果缓存，用FFT结果的圆周移位代替多普勒频移搜索。硬件实现时采用双DDR2 SDRAM缓存，32 K点FFT单核复用的架构，详细描述了算法在FPGA上实现时的逻辑功能划分、核心子模块功能及具体实现方案。通过ModelSim仿真验证，算法提高了数据利用率，减少了捕获时间。

FFT；P码直捕；FPGA实现；双DDR2缓存；分段重叠补零法

于国庆，靳 蕊，李永伟.均值分组块补零P码直捕算法原理及实现［J］.河北科技大学学报，2014，35（2）：172-178.

YU Guoqing，JIN Rui，LI Yongwei.Principle and implement of P-code direct acquisition based on average block zero padding［J］.Journal of Hebei University of Science and Technology，2014，35（2）：172-178.

传统的P码捕获方法是通过接收机先捕获、跟踪C／A码，获得导航电文的转换字HOW，从中获得P码信息以捕获P码［1－5］。但是C／A码的码速率低，码长短，容易受到干扰和攻击，采用直接捕获P码的方式才能充分发挥P码抗干扰和抗截获能力强的特点。针对P码码速率高、码长长的特性，国内外相继提出了很多算法，如：DAVID等和LIN等提出了基于分段补零的循环相关法以及非相干循环相关法［6－7］；YANG等提出的XFAST方法［8］；PANG等提出的重叠平均法［9－10］；近年来国内外很多学者采用基于FFT的伪码相位并行搜索来实现捕获［11－13］。针对大时间不确定度情况下，提出了一种基于FFT的算法，充分利用FPGA的资源和性能，采用外部存储器缓存的高效灵活的P码直捕方法，直接应用Altera的IP核缩短开发时间，并给出了基于该方法的系统实现。

1 基本原理

1.1 基本算法原理

P码的码速率为10.23 MHz，码周期为7 d，传统捕获算法采用时域逐位进行自相关运算，需要大量的串行、并行数据处理，捕获时间长、硬件资源耗费大，不适合于P码的直接快速捕获。基于FFT的捕获由时域转化到频域，利用FFT运算代替相关运算来进行捕获。利用圆周相关定理，如式（1）所示：

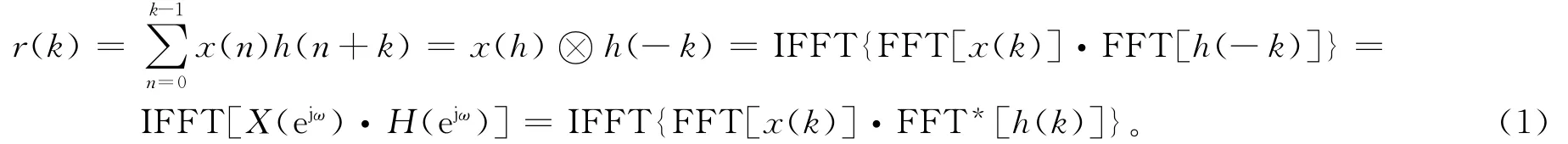
式中：x（n）为接收的信号；h（n）为循环移动的本地码；k为采样点数。很显然直接计算相关值r（k）的计算量很大，而用快速傅里叶变换来计算时，不用将本地码相位一次次移动，而是利用两次FFT和一次IFFT运算求出伪码周期内所有采样点对应的相关值，这样可以大大减少捕获过程的乘法运算，从而大幅度缩短运算时间。这种方法减少了硬件规模，提高了捕获速度，还能抑制窄带干扰，提高接收机的抗干扰性能。

1.2 改进算法原理

在FFT算法的基础上，提出均值分组块补零的算法，充分利用FFT算法的优点，将长码分解成短码并做相应处理，由式（2）可知频域的圆周移位等效于时域的序列调制，所以用FFT结果的循环移位替代多普勒频移搜索，有效提高数据利用率，减少捕获时间。

为了减少FFT运算的长度和次数，加快对时间不确定度的搜索速度，用均值法分别对本地码和接收码进行降速处理。在相同的FFT计算量下，可以将不确定范围扩大至M倍（M点平均），但是均值的点数越多，引入的噪声就会越大，峰值检测性能就会越差，信噪比相应降低。为满足信噪比要求并能有效计算，取M＝4，对本地码和接收码分别进行4点平均。

由于P码周期长，不能直接用相关技术进行计算，必须通过分段补零的方法将超长序列相关运算转化为一系列的子序列的相关，并用FFT循环相关实现序列的线性运算。取2T的接收码和1T的本地码，对本地码补零后再与接收码作相关，结果的前1T数据就为这一子序列的相关值。其中对本地码补零是为了防止无效码的相关引入额外的噪声而降低增益。方案中取T＝1 ms，即相干积累时间为1 ms。

采样频率fs＝62 MHz，经4点平均处理后，等效的采样频率f′s＝15.5 MHz，32 K点FFT变换后，最小分辨频率约473 Hz。即将数据码FFT结果每圆周左（右）移一位数据，相当于进行了473 Hz的下（上）变频。将数据码FFT结果分别左移和右移11次，可以满足多普勒搜索频率范围±5 k Hz。

基于FFT的P码直捕原理框图见图1。

首先连续采集9个1 ms数据段D1—D9，首尾重叠，形成8个2 ms数据段：D1D2，…，D8D9。按照当前时刻，生成8 ms连续本地码C1—C8，在每1 ms本地码后补1 ms的零，最后形成本地码段C10，…，C80。将上述数据段和本地码采用逐次4点平均的方法，将数据量由124 K变换为31 K，再分别补零至32 K，做FFT运算，并将结果分别存储在2个外部存储器DDR2 SDRAM中。

将本地码段C10的32 K点FFT运算结果取共轭与数据段D1D2的FFT结果相乘，再取IFFT变换，取前1 ms数据为二者的相关结果，即相干积累结果，计算其模方并存储。对C20和D2D3，…，C80和D8D9做类似处理，得到的模方求和，即为8次非相干积累的结果。将结果与检测门限相比较，判决是否有信号存在。如果无信号存在，将所有数据段D1D2—D8D9的FFT结果左移（或右移）一位后（改变多普勒频点），再重复上述相关过程，直至判决有信号存在或左移与右移次数各为11次（1 ms的相位搜索），如果未检测到信号，那么需要将本地码相位移至下1 ms。即将C90移入，将C10移出。对新移入的本地码段C90做FFT变换，并将结果存入原C10的FFT结果存储器中。在逻辑上形成C20—C90的连续8 ms的本地码数据。重复上述过程直到捕获到信号或±1 s不确定度时间范围的所有相位均完成搜索。

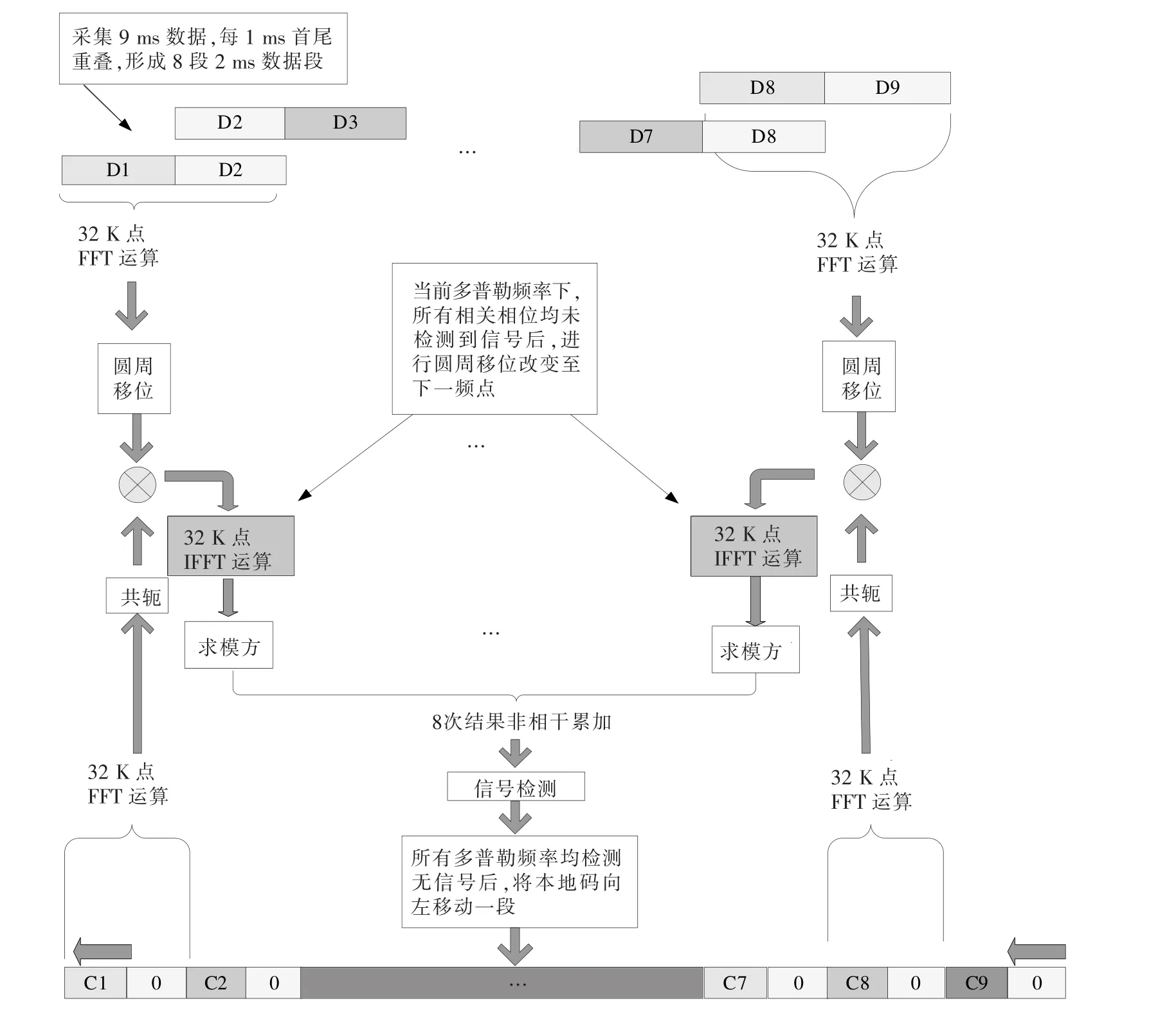
图1 基于FFT的P码直捕原理框图Fig.1 Principle of P-code direct acquisition based FFT

本方案通过直接平均法来降低运算量，用分段重叠补零法将连续的相干积分分解成普通的循环相关进行计算，设计最佳的FFT参数，用傅里叶变换计算循环相关，将接收码和本地码的FFT结果缓存，用FFT结果的圆周移位代替多普勒频移搜索，数据的复用减少了重复采样及变换的时间，提高了数据的利用率，减少了捕获时间。

1.3 数据量分析

A／D转换数据为2位，FFT IP核输入输出数据均采用8位，而且FFT IP核采用块浮点表示法，可以充分利用有限位数据的动态范围。由数字信号处理理论得出式（3）：

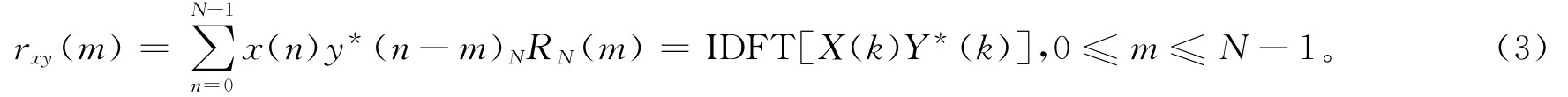
导航中的相关是圆周相关，这里x（n）是接收的导航信号数据，y（n）指本地码数据。y（n）后补一半的零是避免做圆周相关运算时，1 ms之外的数据对结果产生影响。IFFT结果的前一半数据为实际的1 ms相关结果，后一半结果数据舍掉。

载波频率fc＝1 268.52 MHz，采样频率fs＝62 MHz，模拟中频fIF＝46.52 MHz，码速率fp＝10.23 MHz。当相干积累时间TC＝2 ms时，采样点数L＝fs×TC＝124 K。经4点平均处理后，FFT变换的长度N＝31 K，故可在数据后补零至32 768点，用32 K的FFT IP核完成循环相关运算。非相干积累次数M＝8，需要存储总的数据点数为32 K×8＝256 K。与此匹配，本地码的FFT变换结果存储器也需要256 K。数据实部和虚部均用8 bit数据表示，拼成16 bit数据共用一个单元。为了使读写的流程更加顺畅，外挂两片DDR2 SDRAM存储器，将其包装成FFT核读写数据流的格式，选用64M×16结构1 Gbit的DDR2 SDRAM存储器。

2 算法的FPGA实现及仿真结果

2.1 状态机与逻辑控制

根据算法原理，在FPGA中规划设计方案如图2所示。用状态机的思想完成整个设计，算法中用到的FFT和IFFT都是基于1个FFT IP核分时复用实现［14］。为方便处理，设置2片DDR2 SDRAM存储器，且DDR2 SDRAM存储器在同一状态的数据只有一个流向［15］。

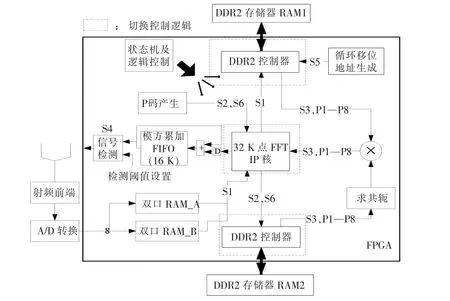
图2 基于FPGA的P码直捕实现框图Fig.2 FPGA based P-code direct acquisition implementation diagram

状态机与逻辑控制模块实现系统主状态机的状态切换，为其他模块提供必要的控制信号。模块各状态描述如表1所示，状态转换图如图3所示。

表1 状态机状态描述Tab.1 State machine described

2.2 接收码采样控制

当状态切换到S1时，对读入的数据码进行A／D变换，并逐次4点平均，为保证实时存储，以15.5 MHz的存储速率存入双口“乒乓”RAM中，然后用高倍速的124 MHz速率首尾重叠的读出数据，每2 ms的数据后面补零到32 K，送入FFT核进行FFT变换，同时生成DDR2写信号，按写信号中的地址将FFT结果存入到DDR2 RAM1相应地址中，当所有需要的数据完成上述过程后向状态机输出结束信号Acquition＿over，状态变为S2。接收码采样处理波形如图4所示。

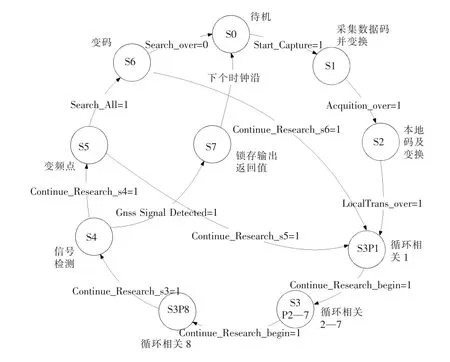
图3 状态转换Fig.3 State transition

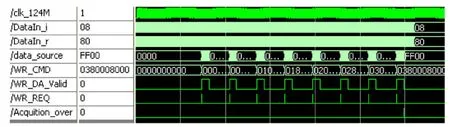
图4 接收码采样处理波形Fig.4 Receiving codes sampling and processing

2.3 本地码采样控制

当状态转换到S2时，从准备好本地码仿真文件中将数据以62 MHz的速率读出，扩位成8位数据，同时采用4点平均的方法降速率至15.5 MHz。将有效的8位数据用FIFO缓冲，以适应FFT IP核需要的124 MHz流入要求。将FIFO中数据读出，每读出1 ms数据后面补零到32 K，送入FFT IP核，同时生成DDR2写信号，按写信号中的地址将FFT结果存入到DDR2 RAM2相应地址中，当所有需要的数据完成上述过程后向状态机输出结束信号Local Trans＿over，状态变为S3。

当状态转到S3时，判断是否取够±1 s时间不确定度的本地码，如果没取够，用62 MHz频率读入下1 ms本地码，将其扩成8位有符号数，进行4点平均，存入FIFO中，如果取够，FIFO中不再存入数据。

当状态转到S6时，对本地码变换的次数进行计数，当计数没有遍历±1 s时，从FIFO中取数，送入FFT核（同S2过程中），同时计算在DDR2中存放本地码的首地址，将FFT结果（8位实部＆8位虚部）和首地址都送给DDR2控制器写端口，FFT输出包尾信号后发出Continue＿Research信号，同时向S3输出本地码的首地址；当计数遍历±1 s时，直接发出Search＿over信号。本地码采样处理波形如图5所示。

2.4 循环移位控制与相干积累控制

按既定的频点生成规律，采用循环移位指针的方法，实现数据FFT结果的左移或右移代替多普勒频移搜索，并在某个确定的码相位下，检测是否所有的频点均已搜索完毕。

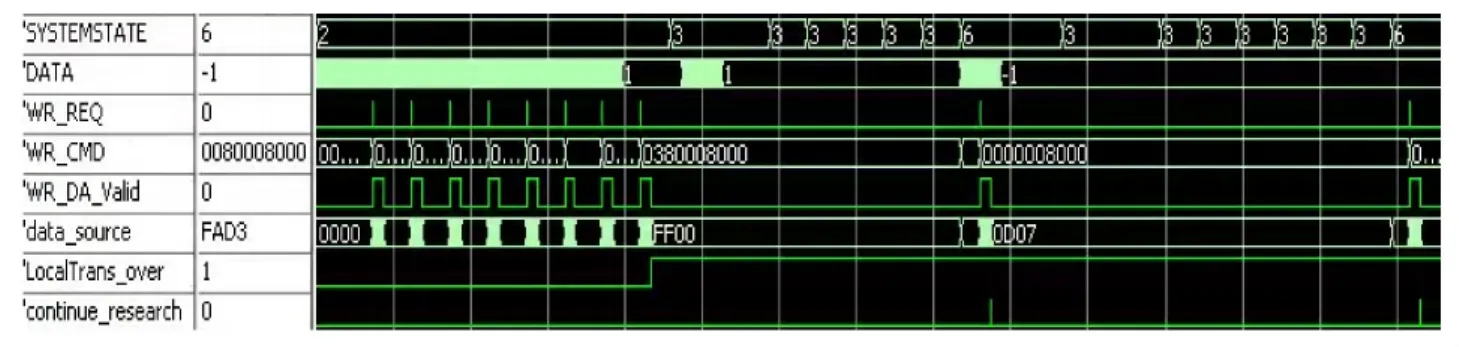
图5 本地码采样处理波形Fig.5 Local code sample processing

按照频点偏移量生成从DDR2中取数的地址，使其能够完成搜索±5 k Hz的多普勒频移，根据地址从DDR2中取出对应数据码和本地码的FFT结果，将本地码FFT结果取共轭后同数据码FFT结果相乘，取出有效位，送入FFT核做逆运算，从而完成相关运算。改变频点偏移量，直至搜索完±5 k Hz或得到想要的相关峰。

2.5 非相干积累与峰值检测

在S3各子状态下，能够通过FIFO的方法，对IFFT的前16 K结果的模方进行累加。

在S4状态下，启动信号检测，将积累结果从FIFO中找出，并逐个与阈值相比较，若大于阈值则认为检测到导航信号存在，向状态机发出GnssSignal＿Detected信号，状态转换到S7，输出相应的值并结束捕获状态；若16 K数据依次与阈值进行比较都不大于阈值，则向状态机发出Continue＿Research信号，状态转换到S5，继续检测。检测大于阈值波形如图6所示。

图6 检测大于阈值波形Fig.6 Accumulated results larger than the threshold

从系统编译综合报告可以看到本文使用的为Cyclone V的5CGXFC7C7F23C8芯片，快速捕获模块系统使用Total block memory bits：8992740 bits，PLLs：2。

3 捕获时间分析

P码直捕模块的内部时钟为124 MHz，调用Altera的IP核采用流式对32 K点的FFT／IFFT进行运算，需要32 768个时钟周期，即完成一次FFT／IFFT运算的时间T1＝32 768／124 MHz＝264.26μs，每缓存1 ms的数据接收数据码和本地码需要T2＝1 000μs。在S1状态时，需要采集9 ms接收数据码进行首尾重叠，由于用流水线的形式采集数据并做FFT运算，所以所用时间TS1≈T2×9＋T1＝9 264.26μs；在S2状态时，需要采集8 ms的本地码后面补零，所以所用时间TS2≈T2×8＋T1＝8 264.26μs；在S3—S5状态只要将缓存的FFT结果按频移等效的地址取出数据做共轭相乘并求IFFT，由于移位次数N＝±11＝23，非相干积累次数M＝8，所以所用时间TS3≈T1×M×N＝48 623.84μs。这样完成第1 ms搜索需要时间TA＝TS1＋TS2＋TS3＝66 152.36μs。在上述过程同时将下1 ms本地码读入，当没有搜索到时需要进入S6状态将下1 ms本地码进行FFT变换，用时T3＝T1，再对当前的数据进行多普勒频移搜索，用时T4＝T1×M×N，完成1 ms检测搜索的P码时间不确定范围为4 ms，搜索±1 s的时间不确定范围需要搜索的码相位段数为500，需要时间TB≈（T3＋T4）×500＝24 444 050μs，所以总的捕获时间约为T＝TA＋TB＝24.5 s。

4 结 语

设计了基于FPGA的P码直捕解决方案，采用均值分组块补零的P码直捕算法，减少直接捕获时间，可大大缩短P码接收机的首次定位时间，充分利用FPGA特性，占用硬件资源少，适合流片。在ModelSim仿真环境下对算法进行验证，结果证实：均值分组块补零的P码直捕算法能够在25 s内完成对多普勒频移为±5 k Hz、时间不确定度为±1 s的P码的搜索，满足系统指标对捕获时间的要求，且比在相同条件下采用基于16 K点FFT重叠平均算法捕获时间减少22 s。

［1］ PETOVELLO M G，DRISCOLL C O，LACHAPELLE G.Carrier phase tracking of weak signals using different receiver architectures［A］.ION NTM 2008 Conference［C］.San Diego：［s.n.］，2008.1023-1033.

［2］ DRISCOLL C O，GERARD L.Comparison of traditional and kalman filter based tracking architectures［A］.European Navigation Conference 2009［C］.Naples：［s.n.］，2009.967-976.

［3］ BORRE K，AKOS D M，BERTELSEN N，et al.A Software-Defined GPS and Galileo Receiver［M］.Boston：Springer Verlag，2006.

［4］ PSIAKI M L.Smoother-based GPS signal tracking in a software receiver［A］.ION GPS［C］.Salt Lake：［s.n.］，2001.2900-2913.

［5］ KAPLAN D E.The Principle and Application of GPS［M］.Beijing：Publishing House of Electronics Industry，2007.

［6］ DAVID M L，JAMES B Y T.Comparison of acquisition methods for software GPS receiver［A］.ION GPS［C］.Salt Lake：［s.n.］，2000.2385-2390.

［7］ LIN D M，TSUI J B Y.A software GPS receiver for weak signals［J］.IEEE MTT-S International Microwave Symposium Digest，2001，3：2139-2142.

［8］ YANG C，JUAN V，JAMES C.Fast direct P（Y）-code acquisition using XFAST［A］.ION GPS［C］.Nashville：［s.n.］，1999.317-324.

［9］ PANG J，FRANK V G，JANUSZ S，et al.Fast direct GPS P-code acquisition［J］.GPS Solutions，2003，7（3）：168-175.

［10］ PANG J，JANUSZ S.Fast direct GPS signal acquisition using FPGA［A］.ECCTD［C］.Kraków：［s.n.］，2003.284-287.

［11］ 张新波，张 扬，刘 田.GPS接收机P（Y）码直捕方法研究 ［J］.电子科技大学学报，2008，37（sup）：62-65.

ZHANG Xinbo，ZHANG Yang，LIU Tian.The GPS receiver P（Y）code direct acquisition method［J］.Journal of University of Electronic Science and Technology，2008，37（sup）：62-65.

［12］ 谢 钢.GPS原理与接收机设计［M］.北京：电子工业出版社，2009.

XIE Gang.Principle of GPS and Design of Receiver［M］.Beijing：Publishing House of Electronics Industry，2009.

［13］ 李玉红，寇艳红，张其善.微弱 GPS信号捕获算法研究［J］.遥测遥控，2009（7）：61-65.

LI Yuhong，KOU Yanhong，ZHANG Qishan.Study on acquisition algorithm of weak GPS signal［J］.Telemetry and Remote Control，2009（7）：61-65.

［14］ 杨伟才，侯 洁，刘玉坤，等.基于FPGA的FFT处理器设计［J］.河北工业科技，2013，30（2）：112-116.

YANG Weicai，HOU Jie，LIU Yukun，et al.Design of FFT processor based on FPGA［J］.Hebei Journal of Industrial Science and Technology，2013，30（2）：112-116.

［15］ 张 阳，王中阳，王红胜，等.基于FPGA的多端口存储控制器设计［J］.河北工业科技，2010，27（6）：401-405.

ZHANG Yang，WANG Zhongyang，WANG Hongsheng，et al.Design of multi-port memory controller based on FPGA［J］.Hebei Journal of Industrial Science and Technology，2010，27（6）：401-405.

Principle and implement of P-code direct acquisition based on average block zero padding

YU Guoqing1，JIN Rui1，LI Yongwei2
（1.School of Information Science and Engineering，Hebei University of Science and Technology，Shijiazhuang Hebei 050018，China；2.School of Electrical Engineering，Hebei University of Science and Technology，Shijiazhuang Hebei 050018，China）

The long period precise ranging code（P-code）is mainly applied to precise positioning service.A new P-code direct acquisition method based on average block zero padding and FFT is provided to reduce the amount of calculation by direct average method.Using piecewise overlapping zero to make continuous coherent integration decomposed into a common cyclic correlation and cache the FFT result of the

code and local codes，and FFT results circumference shift replaces the Doppler shift search.The hardware adopts double DDR2 cache and reuse of one 32 K Point FFT＿IP core.Logic algorithm is implemented on the FPGA，and the function partitioning，and the core sub-module functions and specific implementation plan are described in details.ModelSim simulation shows that it can improve the use ratio of data and decrease the acquisition time.

FFT；P-code direct acquisition；FPGA implementation；double DDR2 cache；piecewise overlapping zero

TN911.7

A

1008-1542（2014）02-0172-07

10.7535／hbkd.2014yx02011

2013-12-26；

2014-02-23；责任编辑：陈书欣

国家自然科学基金（61076052）

于国庆（1969-），男，山东宁津人，副教授，硕士，主要从事测控技术方面的研究。

E-mail：hbkdygq＠163.com