半解析高阶有限谱元法及其在波导介质层PBG结构滤波器优化设计中的应用*

朱宝 钟万勰

(1.大连理工大学材料科学与工程学院表面工程实验室，大连 116023)(2.大连理工大学工程力学系工业装备结构分析国家重点实验室，大连 116023)

引言

电磁模拟中的层状结构经常在许多领域遇到，比如集成光学，地质勘探，电子封装，滤波器［1-3］.由于限元法(FEM)的几何建模灵活性，有限元法被应用于层状结构的全波分析，从而获得层状结构的电磁特性.然而，随着层数的增加，直接使用有限元离散整个结构可能会导致耦合方程的未知数非常庞大，从而使传统的有限元计算效率变得非常低.沿纵向方向的分段均匀性的层状结构，可以被利用来改善传统的有限元分析的效率.数值模态匹配法(NMM)［4］，将3维层状结构分成N个区域.通过二维有限元获得每个区域的本征模态，然后通过引入广义反射和传输算子求解波传播问题.数值模态匹配法可以将3维问题降低成若干二维问题，从而大大减少了未知数，从而降低内存的需要和计算时间.这种方法已经被应用到各种地下探测遥感问题和波导不连续性问题［5-7］.分层有限元法(LAFE)是另一种有效的分析分层结构的有限元方法［8-10］.这种方法可用于在时域和频域模拟.

在这里，我们采用了层状结构的半解析高阶谱元法(SEM).将分段均匀的三维层状结构分为几个沿纵向均匀子结构.采用2维高阶谱单元［11-13］对其横截面进行半解析离散，谱单元是特殊类型的高阶有限单元.然后将半离散的系统从拉格朗日系统转化到哈密顿系统，利用基于Riccati方程的精细积分(HPI)［14-16］方法生成出子结构口刚度矩阵.无论子结构的长度是多少，精细积分法(HPI)都可以达到计算机精度.出口子结构刚度矩阵可以直接组装成具有三对角块状的矩阵形式总体刚度阵.

微波滤波器在微波毫米波通信、卫星通信、雷达、导航、制导、电子对抗、测试仪表等系统中都有着广泛的应用.波导型滤波器是微波滤波器的一个非常重要的分支.近年来微波技术的快速发展对该滤波器的尺寸、阻带特性等指标都提出了越来越高的要求.PBG结构属多谐振结构，优化设计时目标函数和约束函数很难用显式函数表示出来.本文将在辛体系下利用半解析高阶谱元法对矩形波导纵向排列介质层PGB结构(图1)的高精度高效率的分析的基础之上，应用遗传算法对滤波器模型进行全局优化设计，得到滤波性能最优的设计参数.算例表明本文方法相对于其它文献［19-20］给出的算法具有更大的优势.

1 控制方程及变分原理

考察电磁波导的一个区段，其横截面为Ω，而纵向长度有限，两个端面的z轴坐标分别为za、zb.矢量波动方程如下:

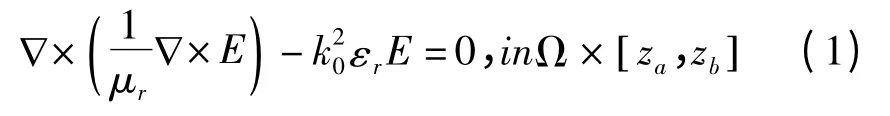
其中εr和μr分别表示相对介电常数和相对磁导率.k0表示在真空中的波数.子结构环向为理想导体边界条件(PEC)和理想磁导体边界条件(PMC)

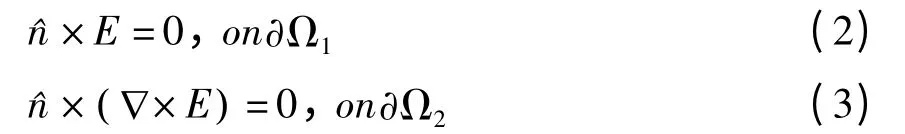
控制方程对应的单变量变分原理为

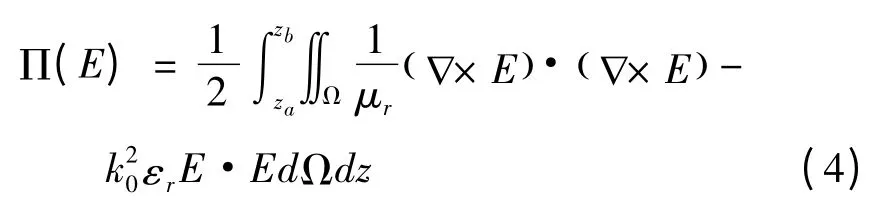
电场E可以分解成横向分量和纵向的分量。

其中

算子∇也可以分解成横向算子和纵向算子

其中

将(5)和(7)代入变分原理，得到

其中

2 分层结构横截面的二维高阶谱单元

二维谱单元用来离散分层结构的子结构横截面.谱单元［11-13］是一种特殊类型的高阶有限元，谱单元采用Gauss-Lobatto-Legendre(GLL)多项式的根作为插值结点，而不是采用间距相等的网格点做为单元的插值结点，这样谱单元可避免著名的龙格现象［17］实现谱精度，这意味着谱单元的数值精度能随着基函数的阶数的增加呈指数级提高.二维标量m阶谱单元基函数为

2D矢量谱单元的基函数包含两个分量

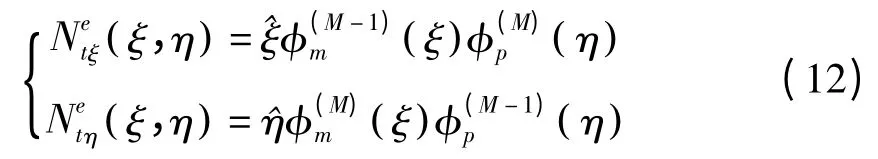
其中

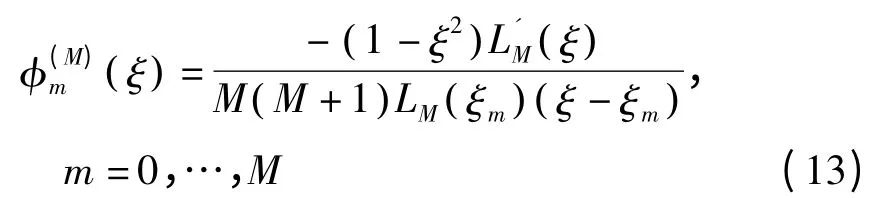
每个单元内的横向场分量和纵向场分量可表示为:

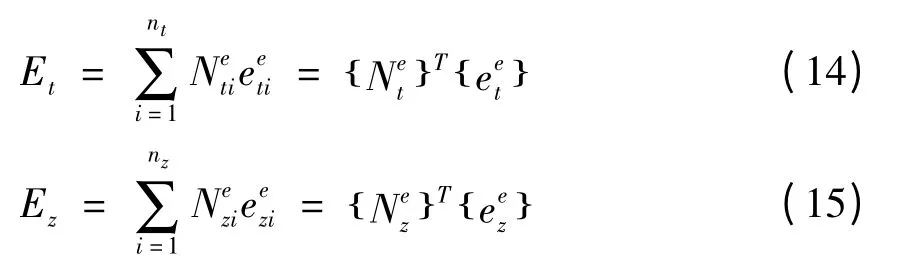
3 半解析系统的出口刚度阵

由上述高阶谱单元离散的子结构横截面，得到

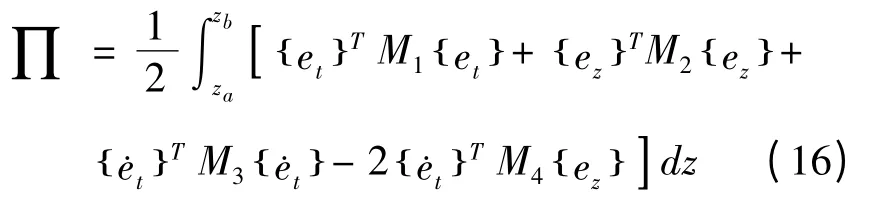
其中

导入Hamilton体系之前，先施加环向的边界条件，然后完成对的变分，有

将其代入(16)，得到Largrangian系统

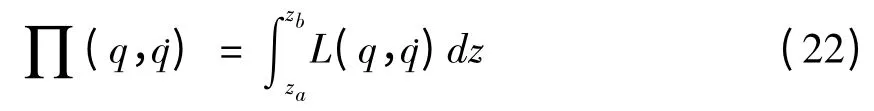
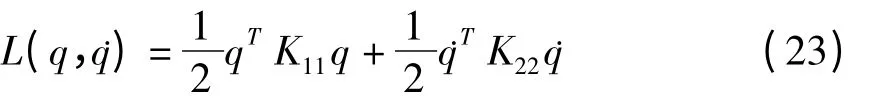
其中

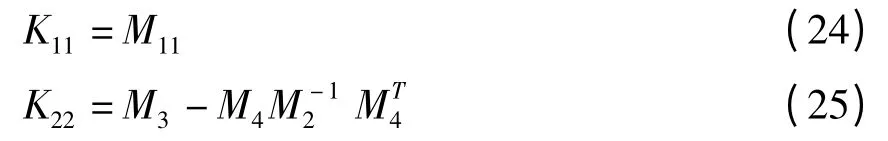
因为环向边界条件已经被加入.根据唯一性理论［18］，如果两端边界条件确定，那么结构中的所有未知量都将确定.

区段势能应该是两端切向电场向量的二次型函数，即

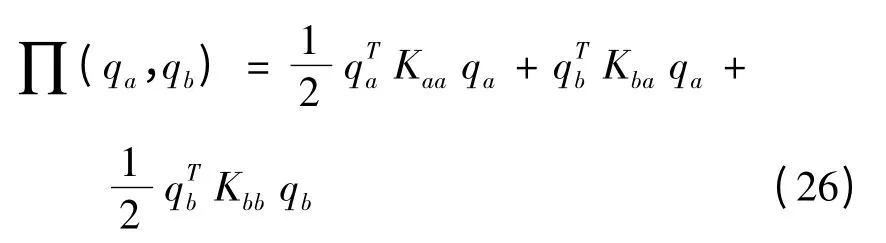
Kaa，Kba和Kbb就是子结构的出口刚度阵.

4 Hamilton系统和Riccati方程

关于(26)的积分并不容易，只能借助于数值积分技术，但这样无法保证积分过程的效率与精度，也失去了半解析有限元的意义.一个可行的思路是将Largrangian系统导入Hamilton系统，再利用Riccati方程精细积分方法进行求解.首先引入对偶变量

这样我们就得到了Hamilton函数

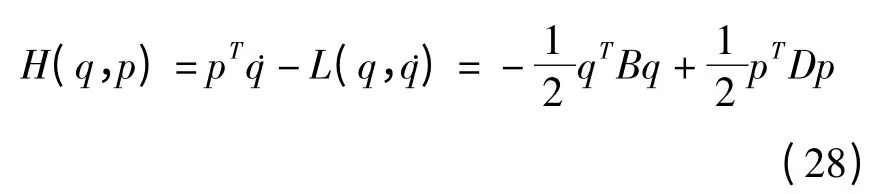
其中

选用波导两端的变量qa，pb作为基本未知量，通过对区段势能的Legendre变换引入波导的区段混合能［13］

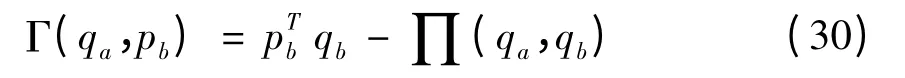
通过对上式的变分可以看出

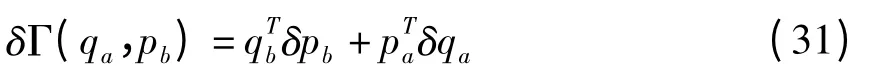
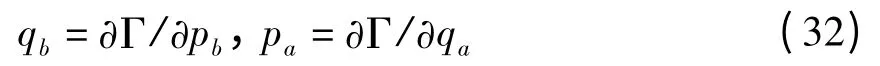
由式(31)可知区段混合能同样是二次型函数，可表达为

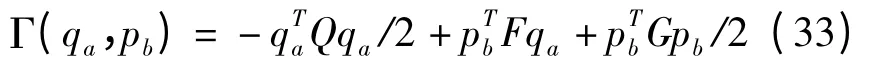
综合(28)、(29)、(30)、(33)即可知矩阵Kaa、Kba、Kbb与Q、F、G是可以相互转化的，其关系如下

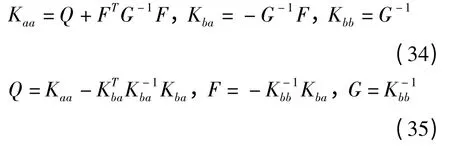
当考虑的波导区段为沿z方向均匀，也即其几何与材料参数沿z坐标不变时，矩阵函数仅是波导的区段长度

的函数，即有Q(η)、F(η)、G(η).相应于区段混合能的矩阵Q(η)、F(η)、G(η)可由相应于区段混合能密度的矩阵B、D积分得到，其关系满足联立Riccati微分方程

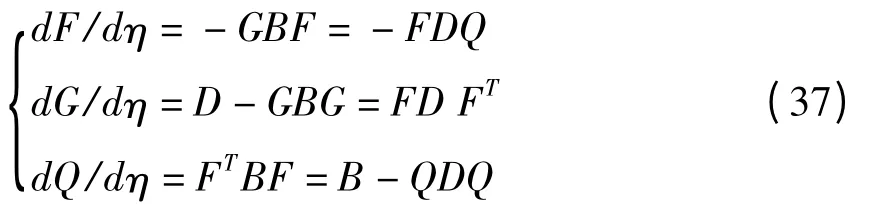
其初始条件为

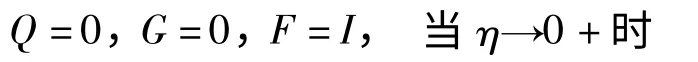
方程(44)看起来很复杂，但可以采用Riccati微分方程的精细积分算法进行求解.精细积分虽然也是一种数值积分方法，但其计算精度可以超过现有计算机字长所决定的精度范围，从某种意义上说，也就是得到了计算机上的解析解.限于篇幅，其详细的公式推导及精度分析可以参考文献［14］.

5 PBG结构滤波器的优化设计

由于光子晶体具有带阻特性，可用于带阻滤波器，而且通常人们希望在阻带内的光透过率越小越好，而在阻带以外的区域透过率越大越好.在阻带宽度一定的情况下，透过率越小，透射系数曲线与横坐标轴(频率坐标轴)所围成的面积应该最大.因此建立优化控制模型［19，20］:

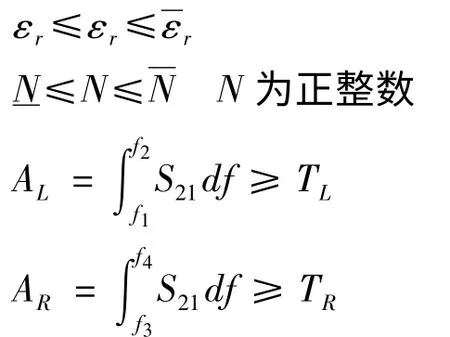
其中空气层厚度a、介质层厚度b、介质相对介电常数εr以及周期个数N为设计变量.向量x=( a，b，εr，N)T表示设计变量向量;f2、f3为阻带边界上下两个频率，f1为阻带所研究频率范围的下边界，f4为阻带所研究的频率范围的上边界;S21为透射系数，为频率f2到f3区间内透射系数曲线与横坐标所围成的面积.AL、AR为相应频率区间内电磁波的透射量.TL、TR为相应频率区间内电磁波的透射量所允许的最小值四个设计变量的上、下限.

6 数值算例

对图1所示的滤波器，设计参数设定为文献［19-20］的优化结果.运用半解析高阶有限谱单元计算该滤波器的散射参数.滤波器横截面分别采用常规有限元和高阶有限谱单元进行离散，所需要的未知数个数、cpu时间、相对误差如表1所示.很显然，高阶有限谱单元无论在精度和效率上都比传统的有限元有更大的优势.也就是说，在达到相同精度的条件下，高阶有限谱单元所需要的计算时间要比传统有限元少很多.半解析高阶谱单元的精度与谱单元阶数的关系如图2所示，表明谱单元的数值精度能随着基函数的阶数的增加呈指数级提高.表明高阶有限谱单元可以达到任意需要的精度.

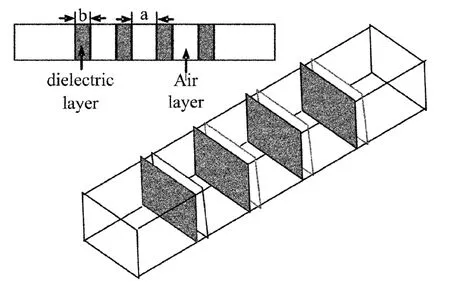
图1 介质层PBG结构滤波器Fig.1 Dielectric layer PBG structures in waveguide

表1 高阶谱元法与传统有限元精度和效率比较Table 1 Semi-analytical SEM with different interpolation orders for transverse discretization

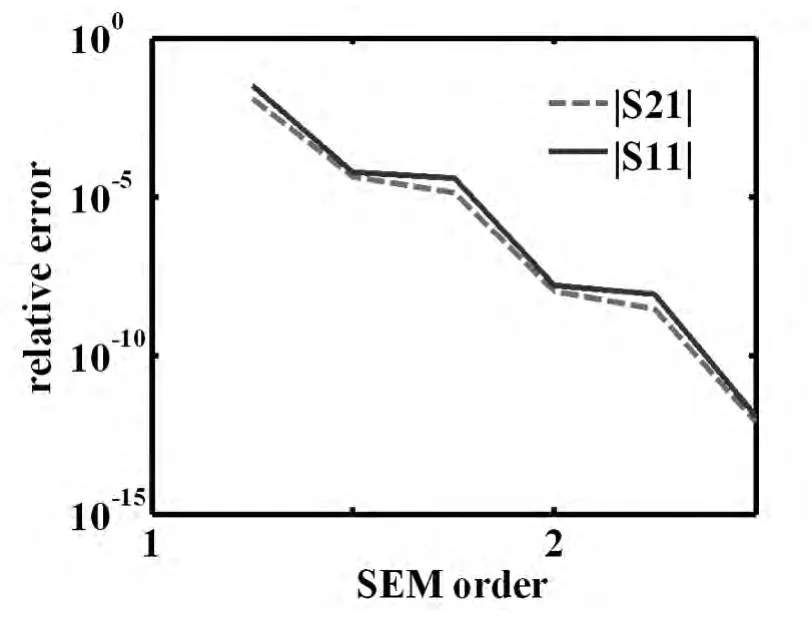
图2 半解析高阶谱单元的精度与谱单元阶数的关系(对数坐标)Fig.2 Relative errors of reflection and transmission coefficients of the microwave filter by the semianalytical SEM with different interpolation orders for transverse discretization

对图1所示的滤波器，设计阻带中心频率约为6GHz、带宽为2GHz的PBG滤波结构.取矩形波导的横向截面尺寸为57mm×23mm，设f1=3GHz，

优化后的设计变量为:a=11.4245mm，b=8.93683mm，εr=2.7354，N=15.目标函数值和设计变量随迭代步的变化规律如图3和图4所示.图5给出了文献［19-20］给出的优化后的结构的阻带特性以及应用本文方法优化后的阻带特性.从图5中可看出文献［19-20］给出的优化后的结构所对应的阻带中心频率大约在6GHz附近，但其阻带不够深;而本文优化后滤波器的阻带中心频率约为6GHz、阻带宽度约为2GHz，且阻带特性好，达到了预期的设计.

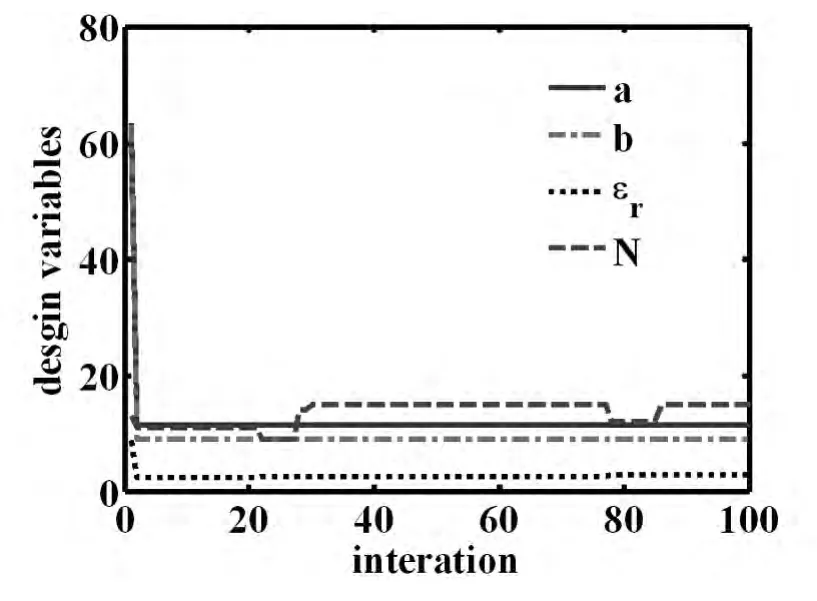
图3 设计变量随迭代次数的变化Fig.3 Design variables versus iteration numbers

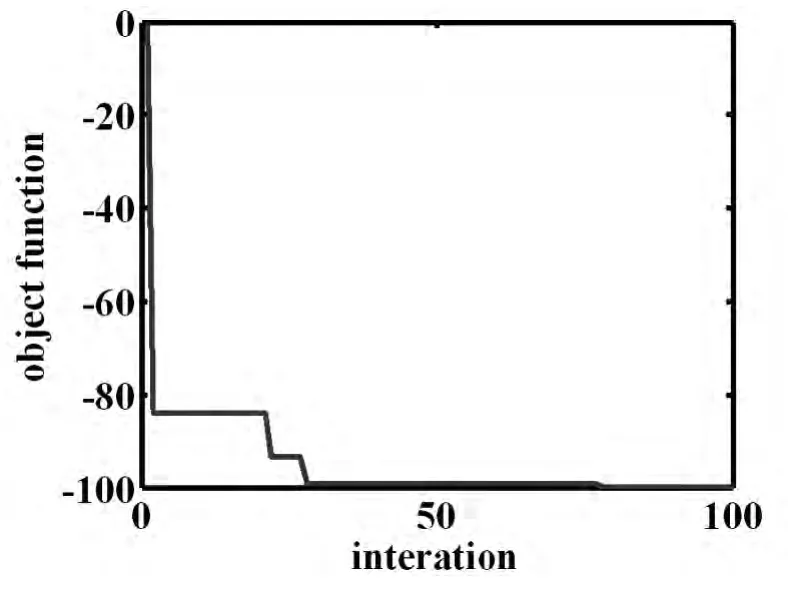
图4 目标函数随迭代次数的变化Fig.4 Object function versus iteration numbers

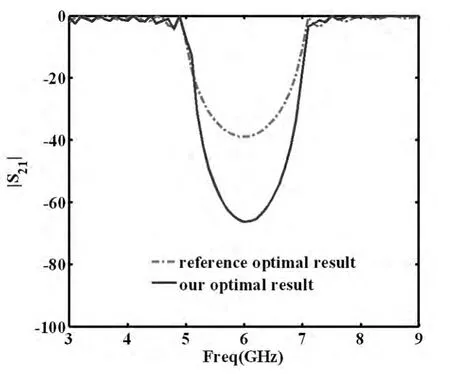
图5 本文优化结果与其它［19，20］优化结果比较Fig.5 Stop-band characteristic for our optimization and other optimization［19，20］

7 结论

本文阐述了高阶有限谱元法结合Riccati方程的精细积分算法求解分层结构的电磁模拟问题的思路，并通过数值算例展示了这种方法具有的谱精度，即谱单元的数值精度能随着基函数的阶数的增加呈指数级提高.以半解析有限谱单元的高精度高效率分析作为基础，应用遗传算法对PBG结构滤波器进行优化.得到了PBG结构滤波性能全局最优的设计参数.表明这种方法在微波器件、集成光学网路的分析和设计中可以发挥很大的作用.

1 Wait J R.Electromagnetic waves in stratified media.New York:Oxford University Press，1970

2 Johnson SG，Joannopoulos J D.Three-dimensionally periodic dielectric layered structure with omnidirectional photonic band gap.Applied Physics Letters，2000，77(22):3490～3492

3 Meuris P，Schoenmaker W，Magnus W.Strategy for electromagnetic interconnect modeling.IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems，2001，20(6):753～762

4 Liu Q H，Chew W C.Numerical mode-matching method for the multiregion vertically stratified media.IEEE Transactions on Antennas and Propagation，1990，38(4):498～506

5 Liu Q H，Chew W C.Analysis of discontinuities in planar dielectric waveguides:an eigenmode propagation method.Transactions on Microwave Theory and Techniques，1991，39(3):422～430

6 Liu Q H.Electromagnetic field generated by an off-axis source in a cylindrically layered medium with an arbitrary number of horizontal discontinuities.Geophysics，1993，58(5):616～625

7 Fan G X，Liu Q H，Blanchard S P.3-D numerical modematching(NMM)method for resistivity well-logging tools.Transactions on Antennas and Propagation，2000，48(10):1544～1552

8 Jiao D，Chakravarty S，Dai C H.A layered finite element method for electromagnetic analysis of large-scale high-frequency integrated circuits.Transactions on Antennas and Propagation，2007，55(2):422～432

9 Gan H，Jiao D.A time-domain layered finite element reduction recovery(LAFE-RR)method for high-frequency VLSI design.Transactionson Antennas Propagation，2007，55(12):3620～3629

10 Gan H，Jiao D.A recovery algorithm of linear complexity in the time-domain layered finite element reduction recovery(LAFE-RR)method for large-scale electromagnetic analysis of high-speed ICs.Transactions on Advanced Packaging，2008，31(3):612～618

11 Kirsch A，Monk P.A finite element/spectral method for approximating the time-harmonic Maxwell system in R3.SIAM Journal on Applied Mathematics，1995，55(5):1324～1344

12 Cohen G.Higher-order numerical methods for transient wave equations.Berlin:Springer，2002

13 Lee J H，Xiao T，Liu Q H.A 3-D spectral-element method using mixed-order curl conforming vector basis functions for electromagnetic fields.Transactions on Microwave Theory and Techniques，2006，54(1):437～444

14 Zhong W X.Duality system in applied mechanics and optimal control.Norwell，MA:Kluwer，2004

15 Zhong W X.On precise integration method.Journal of Computational and Applied Mathematics，2004，163(204):59～78

16 Chen J，Zhu B，Zhong W X.On the semi-analytical dual edge element and its application to waveguide discontinuities.Acta Physica Sinica，2009，58(2):1091～1099

17 Gottlieb D，Hesthaven JS.Spectral methods for hyperbolic problems.Journal of Computational and Applied Mathematics，2001，128(1):83～131

18 Balanis C A.Advanced engineering electromagnetics.New York:Wiley，1989

19 杨红卫，隋永康.波导介质层PBG结构滤波器的优化设计.电讯技术，2007，47(1):60～63(Yang H W，Sui Y K.Optimized design of dielectric layer PBG structure in waveguide filter.Telecommunicat Engineering，2007，47(1):60～63(in Chinese))

20 杨红卫，钟万勰，隋永康.基于响应面方法的波导介质层PBG结构滤波器的优化设计.动力学与控制学报，2007，5(3):193～198(Yang H W，Zhong W X，Sui Y K.Optimal design of dielectric layer PBG structure in waveguide filter on the response surface methodology.Journal of Dynamics and Control，2007，5(3):193～198(in Chinese ))