链式回转弹仓的自适应鲁棒控制
2014-03-01邹权钱林方徐亚栋蒋清山刘艳辉
邹权,钱林方,徐亚栋,蒋清山,刘艳辉
(1.南京理工大学 机械工程学院,江苏 南京210094;2.齐齐哈尔北方机器有限公司,黑龙江 齐齐哈尔161000)
0 引言
链式回转弹仓由各弹筒串联而成,其作用是存储弹丸并根据指令把指定弹丸转送至弹仓取弹口。如果弹仓定位精度较差,将会给取弹带来困难,甚至无法可靠取出弹丸,弹仓的定位精度对取弹可靠性有较大的影响。
随着弹仓中弹丸数量的变化,弹仓的转动惯量、库伦摩擦力矩等将会发生较大的变化,满载时弹仓的转动惯量约为空载时的2 倍,库伦摩擦力矩约为空载时的5 倍。即使在弹丸数量不变的情况下,弹仓的转动惯量也会随其角位置的变化而变化[1],摩擦力矩也会随润滑条件、工作环境等的变化而变化。此外,弹仓采用链传动结构,多边形效应以及轮齿啮合冲击将会产生附加扰动力矩,且链轮齿数越少,附加扰动力矩越大。文献[1]对链式回转弹仓的动力学方程进行了线性化,提出了一种最优保性能控制算法,使用MATLAB 的LMI 工具箱获得了定常状态反馈控制律。文献[2]根据满意控制理论,通过状态反馈配置闭环系统极点,使用MATLB 的NCD 工具箱对控制器参数进行优化,实现了旋转弹仓的鲁棒控制。当弹仓参数发生较大变化时,采用线性定常状态反馈的控制性能可能会有所下降。
目前,处理模型不确定性的方法有H∞最优控制[3]、扰动观测器[4]、滑模控制[5]等。自适应鲁棒控制[6-7](ARC)综合了自适应控制技术和鲁棒控制技术的优点,通过参数在线估计补偿系统参数变化的影响,同时采用鲁棒控制技术处理非线性不确定性的影响,能够获得期望的动态性能和稳态性能。文献[8]针对一类具有参数时变以及非线性不确定性的直线电机位置伺服控制系统,考虑了高频未建模动态的影响,设计了ARC 控制器,获得了渐进跟踪性能。文献[9]针对一类直流力矩电机控制系统,考虑了库伦摩擦和黏性摩擦的影响,通过参数在线估计补偿了非线性摩擦,改善了控制性能。文献[10]针对一类参数大范围变化的直线电机控制系统,考虑了非线性摩擦的影响,针对不同情况分别设计了ARC 控制器,获得了较好的控制效果。文献[11]针对一类非线性不确定多输入多输出(MIMO)系统,设计了一种具有积分型滑模面的滑模控制器,减小了系统的稳态误差。
本文受文献[10 -11]的启发,提出了一种具有积分型滑模面的自适应鲁棒控制算法(ARC-ISS)。在常规ARC 的基础上引入了积分型滑模面,减小了系统的稳态误差。常规ARC 采用定常鲁棒反馈增益,反馈增益大,系统响应快,但容易引起振荡;反之,反馈增益小,系统稳定性好,但响应较慢。为了改善系统的控制性能,当误差较大时,应采用较大的反馈增益以快速减小误差;当误差较小时,应采用较小的反馈增益以防止产生超调并抑制振荡。本文在常规定常鲁棒反馈增益的基础上提出了一种非线性鲁棒反馈增益,改善了系统的动态性能以及稳态性能,获得了较好的控制效果。
1 数学建模及问题描述
链式回转弹仓由工作在力矩控制模式下的永磁直流无刷电机驱动,忽略电流环动态,不考虑永磁直流无刷电机内部的工作方式,链式回转弹仓的动力学方程可以写为
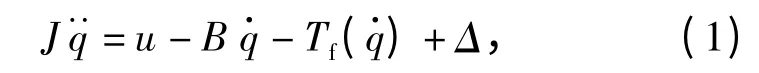
式中:q 为弹仓主动链轮的角位移;u 为控制输入力矩;J 为系统等效转动惯量;B 为系统等效黏性摩擦系数;Δ 为不确定之和,包括高频未建模动态、建模误差、未知外部扰动以及其他难以建模的动态等;Tf()为非线性摩擦,一种工程上常用的非线性摩擦模型[8,10]可以表示为
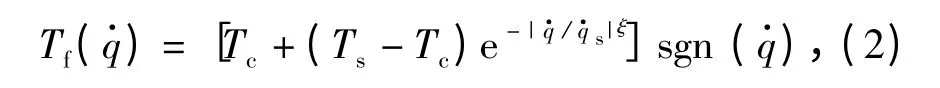
式中:Tc为库伦摩擦力矩;Ts为最大静摩擦力矩;和ξ 为描述Stribeck 效应的参数;sgn(·)为符号函数,可以表示为


假设参考输入信号yd有界,且满足1 阶导数和2 阶导数均连续且有界,则本文研究的问题可看作:设计有界的控制输入u,使得链式回转弹仓的输出角位移y 能够跟踪参考输入信号yd,并且跟踪误差尽量小。
2 模型变换及基本假设
由(2)式可知,非线性摩擦在x2=0 处不连续,而永磁直流无刷电机不能输出不连续力矩,因此无法使用(2)式补偿非线性摩擦。为了解决上述问题,可以采用连续函数(x2)逼近(2)式[9-10],(x2)定义为
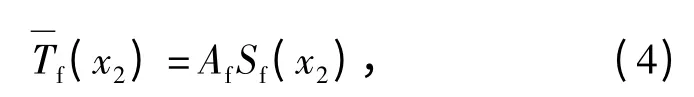
式中:Af>0为未知参数;Sf(x2)=2arctan(100x2)/π. 定义等效扰动则(3)式中的第2 个式子可写为
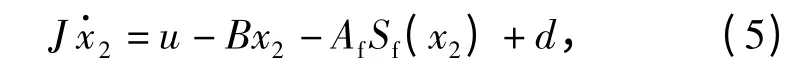
假设等效扰动d 的标称值为dn,定义未知参数向量集合

则由(3)式、(5)式和(6)式可得线性化模型:

考虑到实际系统中J、B、Af、d 均有界,且其边界一般可知或可测,因此有如下假设:
假设1:未知参数集合θ 有界且其边界已知,即存在已知常数θimin、θimax,使得
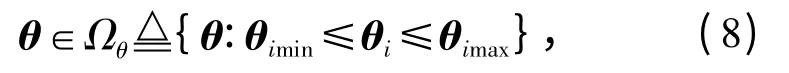
式 中:θimin= [θ1min,θ2min,θ3min,θ4min]T;θimax=[θ1max,θ2max,θ3max,θ4max]T;不失一般性,θ1min>0,θ2min>0,θ3min>0.
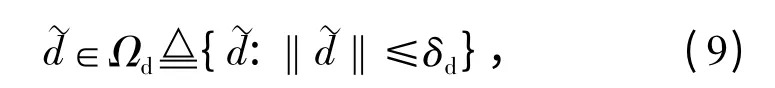
式中:‖·‖表示·的欧几里德范数。
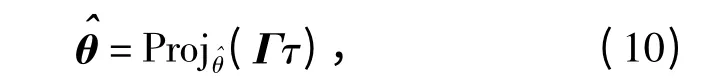
式中:Γ 为待定的正定对角矩阵;τ 为任意的自适应律;Proj^θ(θi)=[Proj^θ(θ1)…Proj^θ(θ4)]T为向量不连续投影算子[8,10],其定义为

对于任意的自适应律τ,不连续投影算子(11)式具有以下性质[6-7]:
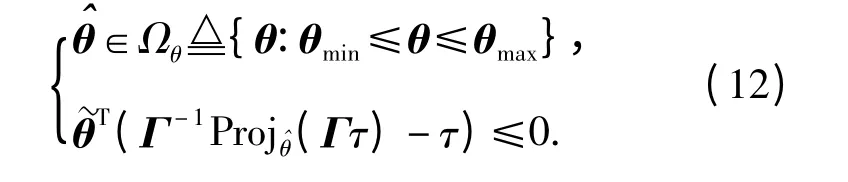
3 控制器设计
定义如下的积分型滑模面

式中:e=y-yd为位置误差;λ >0 为待设计的控制器参数。由(13)式可知从滑模函数p 到位置输出误差e 的传递函数为
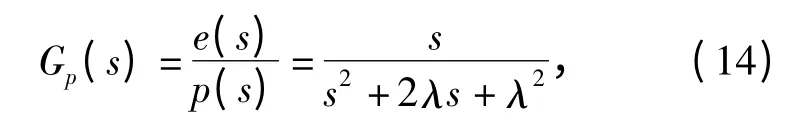
(14)式是一个稳定的传递函数,因此只要p 趋近于0,则e 也趋近于0,且其动态性能可由λ 调整。由(7)式和(13)式可得
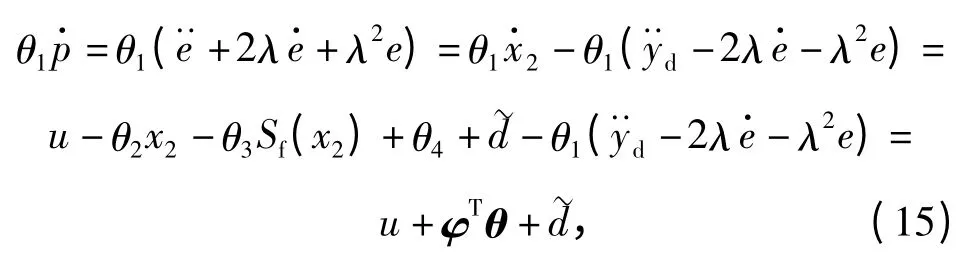
考虑如下的ARC-ISS 控制律:
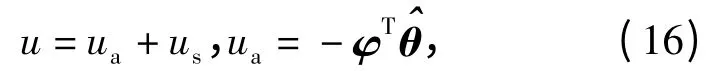
式中:ua为自适应模型补偿项;us为待设计的鲁棒控制项。把(16)式代入(15)式可得
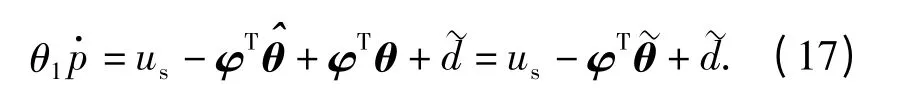
鲁棒控制律us由两部分组成,可以表示为
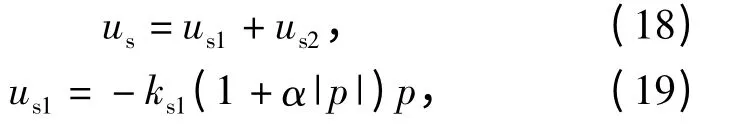
式中:us1为鲁棒镇定项;ks1>0,α >0 为待设计的控制器参数。由(19)式可知,非线性鲁棒反馈增益ks1(1 +α|p|)与滑模函数p 有关,当p 远离零点时,反馈增益增大以使p 快速减小;当p 接近零点时,反馈增益减小以避免剧烈的振荡,因此能够改善系统的动态系能。us2为鲁棒反馈项,用于消除模型不确定性的影响,满足以下条件:
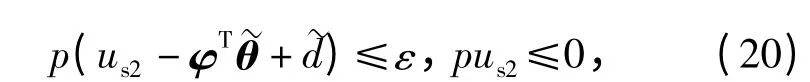
式中:ε >0 为任意大的常数。一种满足(20)式的us2[6,10]可选为

式中:h = (‖φT‖‖θmax-θmin‖)2+ ‖δd‖2. 把(21)式代入到(20)式,可得
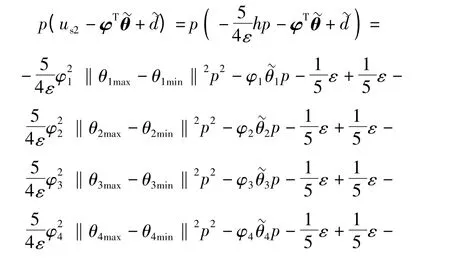
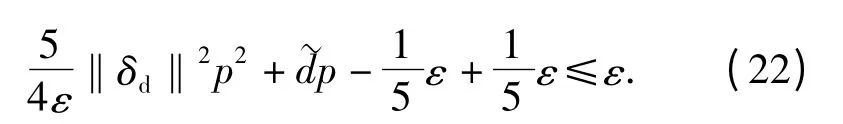
取如下的Lyapunov 函数

注意到(17)式~(19)式和(22)式,(23)式对时间求导可得
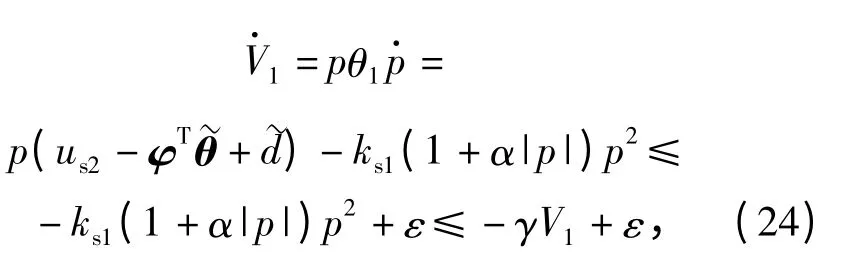
式中:γ=2ks1(1 +α|p|)/θ1max. 因为γ≥2ks1/θ1max,所以当滑模函数p 远离0 时,采用(19)式的非线性鲁棒反馈增益将比常规ARC 具有更快的收敛速度;同时当滑模函数p 接近于0 时,(19)式所示的非线性鲁棒反馈增益约等于常规ARC 中的反馈增益ks1,避免了由于反馈增益过大而引起的振荡。由(24)式可知,V1有界,且其边界满足
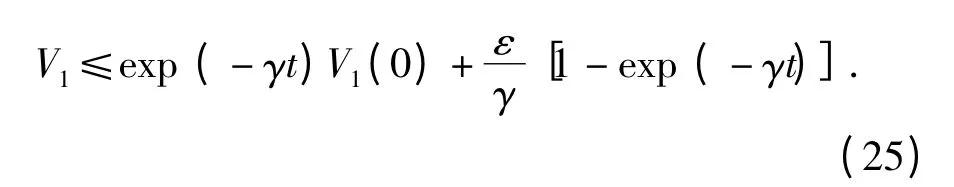
由于V1和θ1有界,由(23)式可知p 有界;由(19)式可知us1也有界;因为参考信号及其导数有界且未知参数的估计值有界,由(16)式和(21)式可知ua和us2有界,所以控制输入u 有界;因此系统所有信号有界。由(25)式可知,当控制律取为(16)式,并且us由(18)式、(19)式以及(21)式给出时,对于任意的自适应律(10)式,系统所有信号有界,且以指数速率收敛于0 的某个邻域内,收敛速度不小于γ,稳态误差的上界可由设计参数ks1、α 和ε 预先设定。
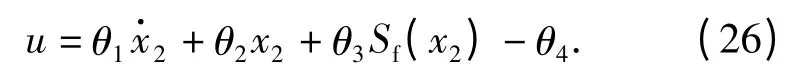
取如下的Lyapunov 函数

假设未知参数θi(i =1,2,3,4)是常数或慢时变的,即≈0(i =1,2,3,4)。注意到(20)式、(27)式对时间求导得
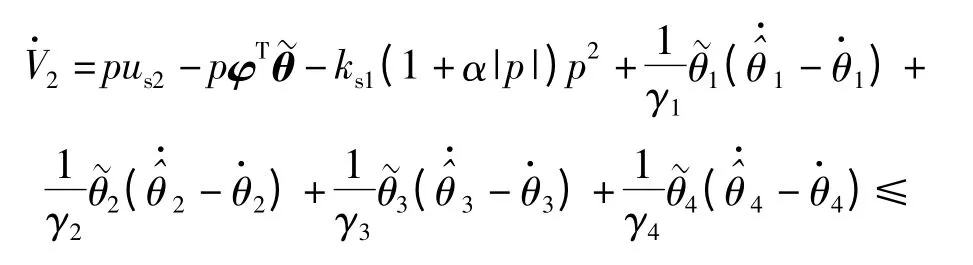
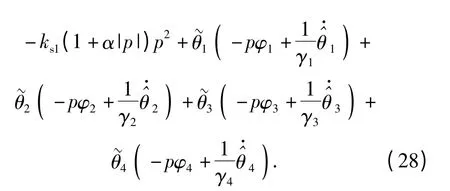
如果自适应律取为
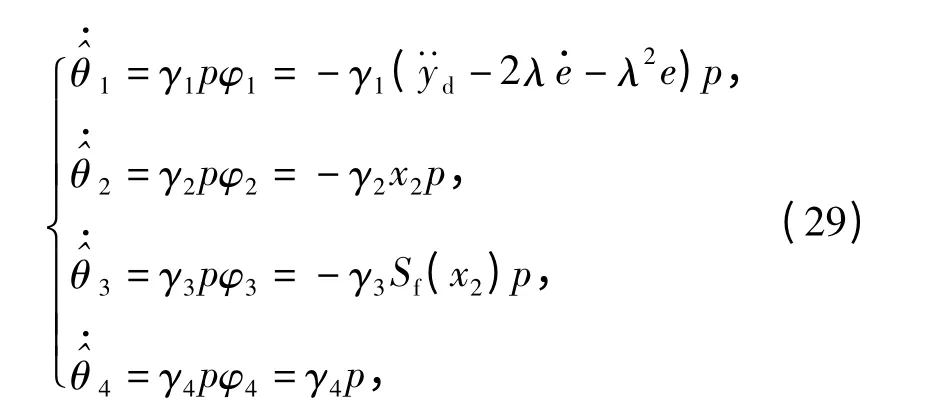
把(29)式代入(28)式,可得
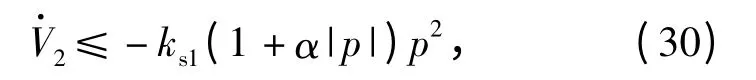
由(30)式可知,当自适应律取为(29)式时,由(7)式、(16)式、(18)式、(19)式以及(21)式构成的闭环系统是稳定的。
4 仿真分析
某链式回转弹仓由永磁直流无刷电机驱动,位置误差要求小于0.4°,控制系统采样周期1 ms. 电机力矩常数为0.057 N·m/A,电机转子转动惯量为1.54× 10-4kg·m2;减速装置等效转动 惯量为0.36×10-4kg·m2,传动比为219.4;弹丸质量为48 kg,弹筒质量为10 kg,满载时弹丸数量为20 个,主动链轮节圆半径为95 mm. 由以上参数可得未知参数集合的边界为θTmin=[10.5,1,50,-100]T,θTmax=[20,30,250,100]T,未知参数初始值取为(0)=[15,20,50,0]T. 非线性摩擦模型(2)式中的参数取为s=0.1°/s,ξ=2. 由(25)式可知,系统动态误差与初始状态有关,为了减小动态误差,有必要对参考信号进行规划以满足:x1(0)= yd(0),x2(0)=本文中采用点到点(PTP)运动轨迹规划,期望位移120°,最大速度66.67°/s,最大加速度333.34°/s2. 由于弹仓中弹丸数量的情况较多,本文仅考虑3 种特殊情况,即:空载(弹仓不装弹丸),半载(弹仓装载10 发弹丸且连续排列),满载(弹仓装载20 发弹丸)。为了验证本文提出的ARC-ISS 算法的有效性,针对上述3 种特殊情况分别对常规ARC 以及ARC-ISS 进行了仿真测试。常规ARC 控制器采用PD 型滑模面,即滑模函数取为p=+λe,控制器参数设置为:λ=10,ks1=1,α=0,ε=10 000,γ1=0.2,γ2=1,γ3=20,γ4=10;ARCISS算法采用积分型滑模函数(13)式,控制器参数设置为:α=5,其余参数同常规ARC.
图1~图3分别为空载、半载、满载时链式回转弹仓的位置跟踪误差,可见常规ARC 和ARC-ISS 均可以获得满意的控制性能;与常规ARC 相比,ARCISS 不仅减小了系统的稳态误差,并且明显地改善了系统的动态性能,具有更快的收敛速度以及更好的控制性能。此外还可以看出,系统参数变化对ARC-ISS 的影响较小,在空载、半载、满载3 种情况下的位置误差均小于常规ARC.
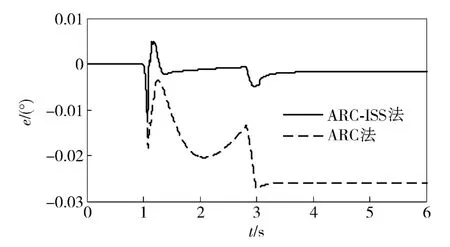
图1 空载时弹仓位置跟踪误差Fig.1 Position tracking errors of shell magazine for empty-loading
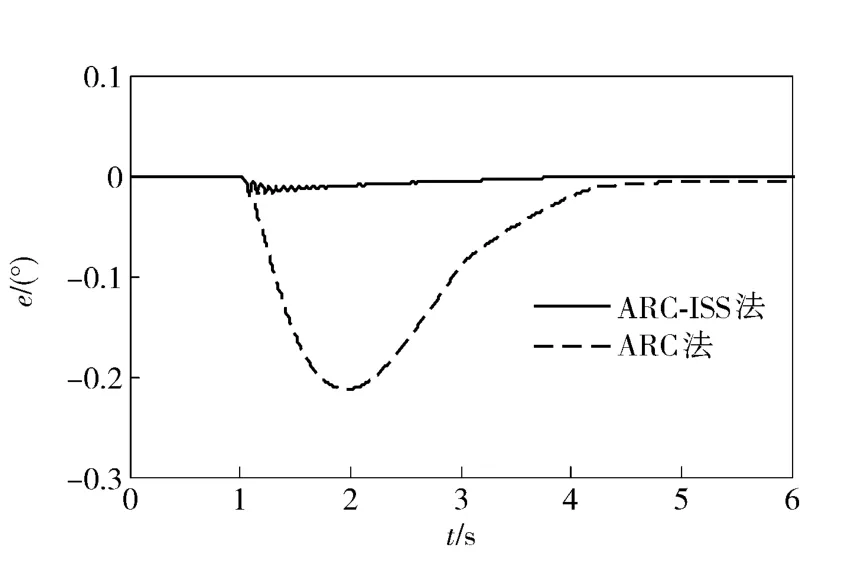
图2 半载时弹仓位置跟踪误差Fig.2 Position tracking errors of shell magazine for half-loading
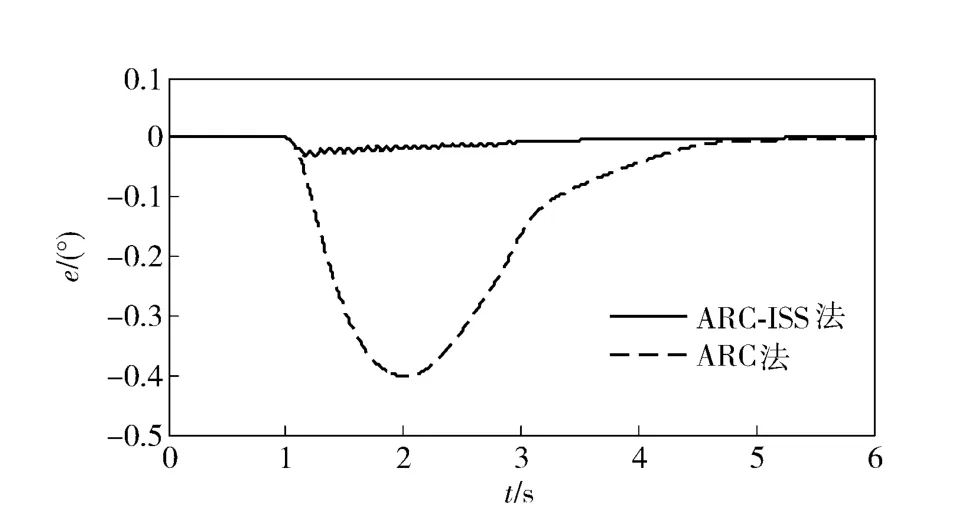
图3 满载时弹仓位置跟踪误差Fig.3 Position tracking errors of shell magazine for full-loading
图4~图7分别为系统未知参数θ1、θ2、θ3、θ4的估计值,可以看出,在空载、半载、满载3 种情况下参数估计值均能保持在有界闭集Ωθ之内,保证了系统的稳定性。
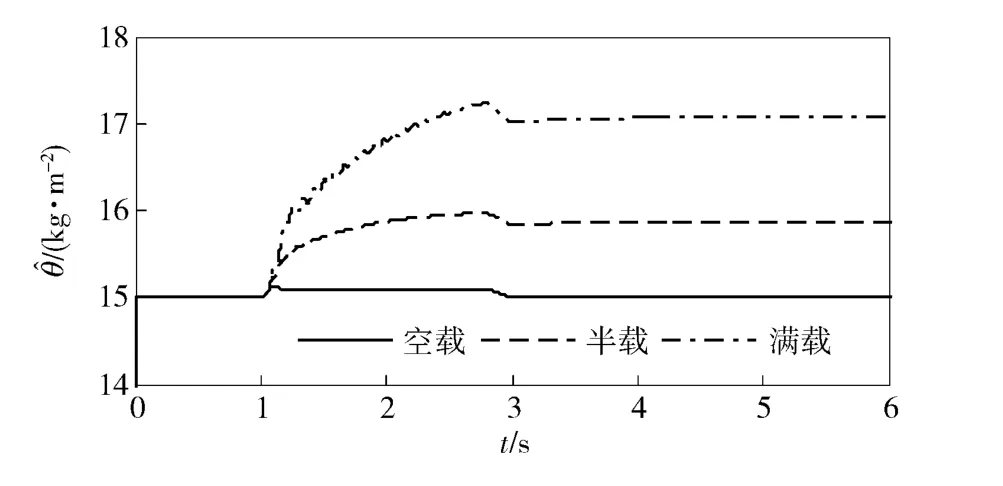
图4 θ1的估计值Fig.4 Estimated values of θ1

图5 θ2的估计值Fig.5 Estimated values of θ2
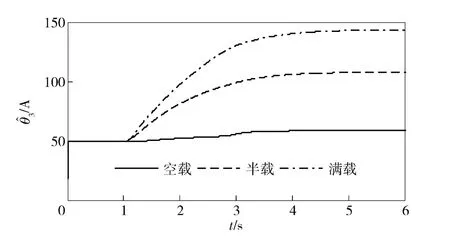
图6 θ3的估计值Fig.6 Estimated values of θ3
由仿真结果可知,与常规ARC 相比,ARC-ISS采用非线性鲁棒反馈增益,当误差较大时,通过引入附加的鲁棒反馈项-α|p|p 使误差快速减小,而当误差趋近于0 时,ARC-ISS 退化为常规ARC,有效避免了高增益可能引起的振荡,ARC-ISS 具有更好的控制性能。在常规ARC 中,需要采用较大的自适应速度以便有效地补偿模型不确定性,但自适应速度过大时,容易引起参数估计不收敛,而ARC-ISS 采用非线性反馈增益,有效地克服了这一缺点,即使采用较小的自适应速度也能够获得满意的控制效果。
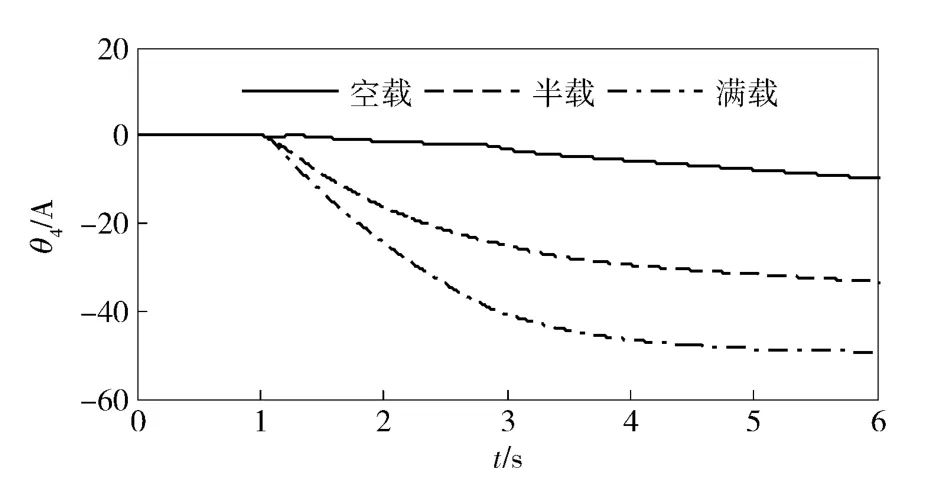
图7 θ4的估计值Fig.7 Estimated values of θ4
5 结论
在自行火炮弹药自动装填系统中,随着弹丸数量的变化,链式回转弹仓的转动惯量、摩擦力矩等将会发生较大的变化;在弹仓高速转动过程中,齿轮与链轮啮合冲击以及链传动的多边形效应会产生附加扰动力矩;为了解决上述问题,本文提出了一种具有积分型滑模面的自适应鲁棒控制算法,采用积分型滑模面减小了系统的稳态位置误差;使用非线性增益鲁棒反馈技术,改善了系统的控制性能,大大提高了系统的响应速度。由于非线性鲁棒反馈增益的作用,即使采用较小的参数估计速度,也能有效地抑制模型不确定性的影响,明显地减小了系统动态跟踪误差。针对空载、半载和满载3 种典型情况进行了仿真实验,结果表明ARC-ISS 比常规ARC 具有更好的控制精度以及更快的响应速度。
References)
[1] 侯保林,马建伟. 链式自动化弹仓的最优保性能控制算法[J]. 兵工学报,2009,30(9):1164 -1169.HOU Bao-lin,MA Jian-wei. Optimal guaranteed cost control algorithm for automatic chain shell magazine[J]. Acta Armamenarii,2009,30(9):1164 -1169.(in Chinese)
[2] 马建伟,郭治,侯保林. 旋转弹仓的鲁棒控制器设计[J]. 火力与指挥控制,2006,31(10):783 -785.MA Jian-wei,GUO Zhi,HOU Bao-lin. Robust controller design for mechanized eddy magazine[J]. Fire Control and Command Control,2006,31(10):783 -785. (in Chinese)
[3] Liu Z Z,Luo F L,Rahman M A. Robust and precision motion control system of linear motor direct drive for high-speed XCY table positioning mechanism[J]. IEEE Transactions on Industrial Electronics,2005,52(5):1357 -1363.
[4] Liu H,Li S. Speed control for PMSM servo system using predictive functional control and extended state observer[J]. IEEE Transaction on Industrial Electronics,2012,59(2):1171 -1183.
[5] Li Y M,Xu Q S. Adaptive sliding mode control with perturbation estimation and PID sliding surface for motion tracking of a piezodriven micromanipulator[J]. IEEE Transactions on Control Systems Technology,2010,18(4):798 -810.
[6] YAO B. High performance adaptive robust control of non-linear systems:a general framework and new schemes[C]∥The 36th IEEE Conference on Decision and Control.San Diego,California,US:IEEE,1995 :2500 -2505.
[7] YAO B,Tomizuka M. Adaptive robust control of SISO non-linear systems in a semi-strict feedback form[J]. Automatics,1997,33(5):893 -900.
[8] Chen Z,Yao B,Wang Q F. Adaptive robust precision motion control of linear motors with high frequency flexible modes[C]∥The 12th IEEE International Workshop on Advanced Motion Control.Sarajevo:IEEE,2012:25 -27.
[9] Chen Z P,Gan M G,Fang H,et al. Adaptive robust dynamic surface control of DC torque motors with true parameter estimates[C]∥2010 American Control Conference. Baltimore,Maryland,US:AACC,2010:3524 -3529.
[10] YAO B. Advanced motion control:from classical PID to nonlinear adaptive robust control[C]∥The 11th IEEE International Workshop on Advanced Motion Control. Nagaoka:IEEE,2010:815 -829.
[11] Zeinali M,Notash L. Adaptive sliding mode control with uncertainty estimator for robot manipulators[J]. Mechanism and Machine Theory,2010,45(1):80 -90.
