谐振子势阱下二维氢原子的运动
2014-02-28许宁
许宁
(遵义师范学院物理与机电工程学院,贵州遵义563002)
谐振子势阱下二维氢原子的运动
许宁
(遵义师范学院物理与机电工程学院,贵州遵义563002)
运用龙格-库塔法解决了被囚禁在谐振子势阱下的二维氢原子的运动情况,得到了氢原子的轨迹图。由运动轨迹图得出:不同能量值的氢原子的运动有不同特性,并且同一能量值下不同初始条件的氢原子的运动也呈现不同特性。
四阶龙格-库塔法;谐振子势阱;二维氢原子
数学物理学是以研究物理问题为目标的数学理论和数学方法。它探讨物理现象的数学模型,即寻求物理现象的数学描述,并对模型已确立的物理问题研究其数学解法,然后根据解答来诠释和预见物理现象,或者根据物理事实来修正原有模型。物理问题的研究一直和数学密切相关。在工程科学中,处处需要精确地求解物理问题,所以数学物理对于技术进步也有非常重要的意义。
1 模型的建立[1-3]
1.1 问题描述
一个氢原子核固定在偏离坐标轴中心O的某位置,核外有一个电子受到其作用力,该电子在谐振子势为中运动,研究该电子的运动情况。假定该氢原子的能量E是恒定的,即为定态。经典力学中,在稳定约束下,哈密顿量H就等于力学体系下的总能量E。其中分别为电子的横坐标和纵坐标。
2.2 模型描述

由谐振子模型可以得到:

对式(8)进行四阶龙格库塔方法处理;已知:

由于式(9)为二元方程,而式(8)为五元方程组,所以需对式(9)进行拓展变形。

则根据上面可以得到Z1,Z2,Z3,Z4:分别对应四个K值,共16个K值;我们不妨设:

同理可以设其他K值。即:

这里i取1,2,3,4;分别代表Z1,Z2,Z3,Z4的下标。
于是有:

其中i=1,2,3,4;j为迭代次数,j=0,1,2,......;
确定步长为h,也就是分别对应Zi(j)和Zi(j+1),可以通过求得Zi(j)的值来求出Zi(j+1),其中上面的i=1,2,3,4;i=0,1,2,3,4……。由龙格库塔方程表达式可知:

3 谐振子势阱下二维氢原子的运动[4-5]
分别取三组不同的初始值
(1)设置初始值,输入程序中,得到数据,画出轨迹图如图1。

图1 E=1,60s轨迹图
从图1可以看出,电子在初始条件x0=1,y0=0,下运动60s,电子被限制在一定范围(-0.75<x<1.25;-1.5<y<1.5)内运动,并且轨迹几乎充满了整个被限制区域。左右两侧边缘形似双曲线。
(2)设置初始值

图2 E=1,700s轨迹图
从图2可以看出,电子在初始条件x0=0,y0=0,x0=下运动700s,电子几乎在几个方向上做来回直线摆动运动。
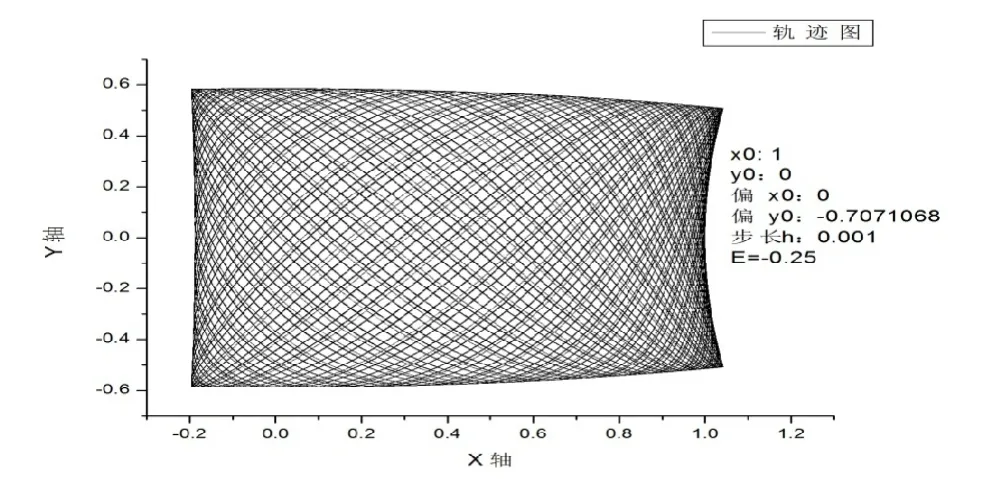
图3 E=-0.25,700s的轨迹图
从图3可以看出,电子在初始条件x0=1,y0=0,下运动700s,电子被限制在一定范围(0.2<x<1.1;-0.6<y<0.6)内运动,且轨迹充满了整个被限制区域。右侧边缘形似双曲线。
4 结论
从轨迹图可以看出,氢原子的运动被囚禁在谐振子势阱中,不同能量值,运动轨迹不同。不同能量值氢原子的运动有不同特性,并且同一能量值下不同初始条件氢原子的运动也呈现不同特性。
[1]Boiteux M.The three-dimensional hydrogen atom as a restrictedfour-dimensionalharmonicOscillator[J].Physica,1973,65:381.
[2]Cornish F H J.The hydrogen atom and the fourdimensional harmonic oscillator[J].J Phys,1984,A17:323.
[3]HARONOVY,ANANDAN J.Phase change during a cyclic quantum[J].Phys Rev Lett,1987,58:1593.
[4]ONES J A,VEDRL V,EKERT A,et al.eometic quantum computation using nuclear magnetic resonance[J].Nature,2000, 403:869.
[5]BULGAC A.On the effective action for a nonadiabatic quatum process[J].Phys Rev,1988,A37:4084.
(责任编辑:朱彬)
Two-Dimensional Hydrogen Atoms Under Harmonic Oscillator Potential Trap
XU Ning
(School of Physics and Mechanical&Electrical Engineering,Zunyi Normal College,Zunyi 563002,China)
The Runge Kutta method has been used to solve the motion of two dimensional hydrogen atom under the harmonic oscillator potential trap,and the hydrogen atom trajectory and Poincare diagram has been gotten.We have drawn a conclusion:the motion of the hydrogen atoms with the different energy values have different characteristics,and the motion of the hydrogen atoms also show different characteristics with the same energy values and different initial conditions.
Fourth-order Runge-Kutta method;Harmonic oscillator potential trap;Two-dimensional hydrogen atoms
O411
A
1009-3583(2014)-0086-03
2014-07-15
许 宁,男,贵州遵义人,遵义师范学院物理与机电工程学院副教授。
