制导系统设计参数多准则优化决策方法研究

张一航，侯明善

( 西北工业大学自动化学院，陕西西安 710072)

0 引言

制导系统作为制导武器系统的核心，其设计性能在很大程度上也决定了武器系统的性能。制导系统的性能与各子系统的设计和参数有着密切的关系，从系统和成本的观点看，在满足制导回路总体性能的基础上，制导系统设计应同时兼顾系统精度高、子系统的协调性好、成本低等多种要求。

制导系统通常包含弹目运动学、导引头、制导指令计算、控制系统和动力学环节等。制导系统属于本质非线性系统，因此系统的设计、优化与决策十分复杂。为减少系统设计的难度，传统上制导系统采用由内向外分别设计的方法，即先设计控制回路再设计制导回路。这种设计方法的基础是需要预先确定各子系统的指标要求，即制导系统子系统设计指标要由系统总体设计预先确定。

采用理论方法进行制导系统总体指标和分系统指标制定几乎难以实施，一般采用系统总体框架设计、子系统建模和仿真计算相结合的方法确定指标。在系统仿真过程中，需要考虑大量不同的初始拦截条件、目标机动方式、子系统模型参数变化范围等因素，这些因素的排列组合会导致仿真计算量激增，而根据大量仿真计算结果决策出一组最优设计参数，或从备选方案中决策出符合要求的系统方案也由于因素众多面临重重困难[1－2]。

近年来，系统工程领域的多准则决策方法在复杂系统设计中受到普遍重视。多准则决策方法能够综合考虑和处理多个相互制约的决策准则，是多属性条件下进行多设计方案比较、排序和选择的有效方法。1981 年，Hwang 等提出了处理多因素决策的优劣解距离法(TOPSIS)[3].TOPSIS 后来得到充分发展和广泛应用，Andrew 等将此方法用于高速导弹DKM119 的设计决策[4]，文献[5 －6]则研究了该方法在高速民航飞机项目(HSCT)的技术评估与方案选择中的应用，Bao 等结合TOPSIS 方法和模糊理论，对道路安全性能进行了设计和评估[7]，Chen 等用TOPSIS 方法设计移动终端的用户界面[8]，都取得了良好的效果。

本文针对制导系统设计参数优化决策问题，提出将多参数、非线性系统的优化设计问题转化为多准则决策问题，为系统设计参数的一体化决策奠定了良好的基础。通过对制导系统性能和成本的需求分析，确定了优化决策准则。以TOPSIS 决策方法结合平面拦截制导系统为例，对提出的方法进行了决策验证。

1 制导系统设计参数决策问题描述

1.1 制导系统模型

考虑平面拦截制导问题，弹目运动关系如图1所示。

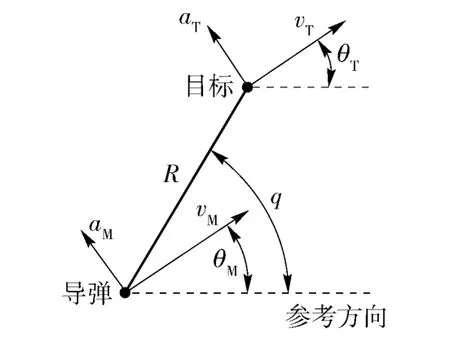
图1 平面拦截几何Fig.1 Plannar intercept geometry

根据图1，弹目相对运动关系为

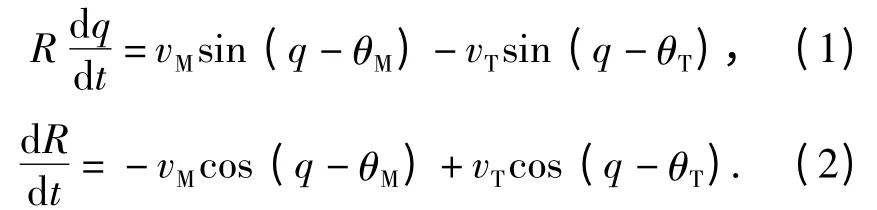
式中:R 表示弹目距离;q 表示弹目视线角;vM和vT分别表示导弹和目标的速度;θM和θT分别表示导弹的弹道倾角和目标的航迹角。

导弹弹道倾角θM与其法向加速度aM、目标航迹角与其法向加速度aT满足关系:

考虑如图2 所示的制导系统结构，它由目标动力学、弹目相对运动关系、导引头动力学、制导律、制导指令限幅和导弹动力学组成。

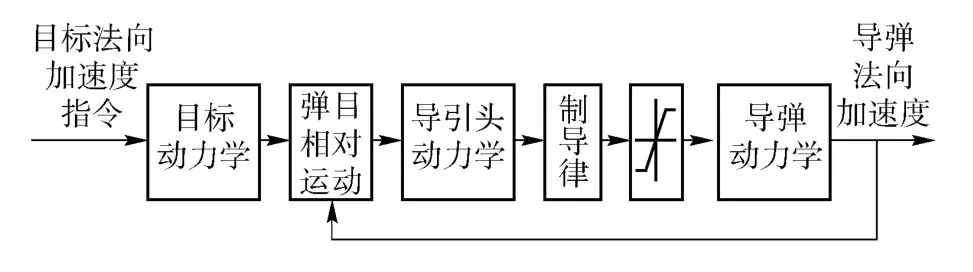
图2 制导系统结构图Fig.2 Block diagram of guidance system

设制导系统制导律为比例导引，则导弹的法向加速度指令aMC的表达式为

式中:N 为比例导引导航比。导弹法向加速度指令受弹体最大可用过载约束，设过载限幅值为nzm，则附加限幅的加速度指令为

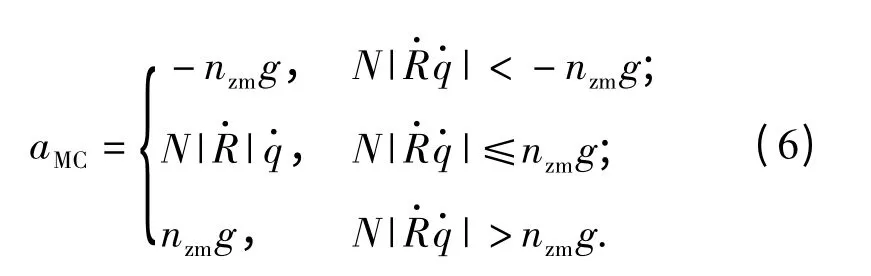
导引头动力学特性用带延迟环节的一阶惯性环节描述，其传递函数为

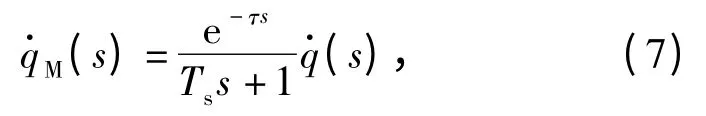
式中:τ 是纯延迟环节的延迟时间;TS表示导引头动力学时间常数是导引头测量的视线角速率，其输入是弹目视线角速率

导弹弹体动力学等效模型用二阶环节描述，其传递函数为

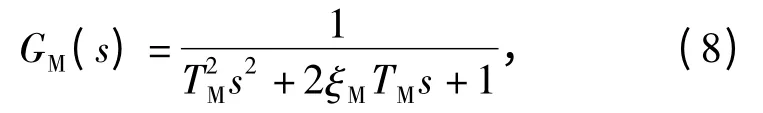
式中:TM、ξM分别表示弹体动力学模型的时间常数和阻尼比。

目标动力学模型同样用二阶环节来描述，传递函数为

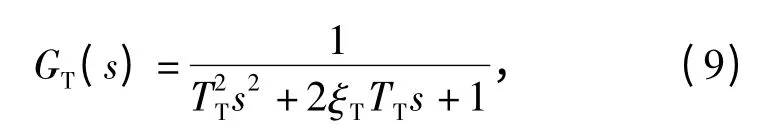
式中:TT和ξT分别表示目标动力学模型的时间常数和阻尼比。

1.2 设计参数和决策准则的选取

前面给出了导弹制导系统的模型，系统共涉及5 个主要设计参数，分别是弹体等效时间常数TM和阻尼比ξM，导引头延迟时间τ，比例导引导航比N 和导弹法向加速度指令限幅值nzm.这5 个设计参数的每一种取值组合，就是制导系统设计中的一种备选设计方案。利用多准则决策方法对不同备选方案进行排序，可决策出多准则意义下的最优方案。

在决策准则的确定中，主要考虑以下3 个因素:

1)制导系统不同发射初值条件下的脱靶量应尽可能小。由于脱靶量的散布，需要建立两个决策准则:脱靶量样本均值d 和样本方差应最小。

2)比例导引导航比N 不应过大。导航比N 过大容易造成制导系统耦合加重，稳定性降低。据此可建立决策准则:在保证命中精度前提下，导航比N应在一定范围内应取较小值。

3)应尽量降低制导控制系统的成本，减少控制能量消耗。导引头的延迟时间τ 越小，对导引头的性能要求就越高，成本也越高;导弹法向加速度指令限幅值nzm的幅值越大，控制过程中消耗的能量也越大，成本也越高。因此，考虑成本问题，建立两个决策准则:导引头延迟时间的倒数1/τ 应尽量小，弹体法向加速度指令的限幅值nzm尽量小。

基于上述5 个决策准则，当有m 个备选方案时，可建立如下m×5 的决策矩阵DM.

式中:Alti是第i 个备选方案;d、N、1/τ、nzm是5 个决策准则。每个备选方案中，N、1/τ、nzm可由设计参数直接得到，而需要通过仿真计算得到。

2 TOPSIS 方法决策过程

TOPSIS 方法基于如下思想:在决策问题的一个有限解集中，最优解与理想最优解(Ideal Solution，IS)的欧氏距离应最近，与理想最劣解(Negative－Ideal Solution，NIS)的欧氏距离应最远[6]。TOPSIS 方法通过对确定性决策问题的有限解集进行排序得到“最优解”。同时，在给定置信度条件下也能对随机决策问题的解集进行排序。

根据文献[6]，TOPSIS 方法对DM 进行了如下六步操作:

步骤1 建立归一化决策矩阵，使得不同决策准则之间具有可比性。方法是将DM 中的每个元素除以该元素所在列向量的2 范数，如(11)式所示:

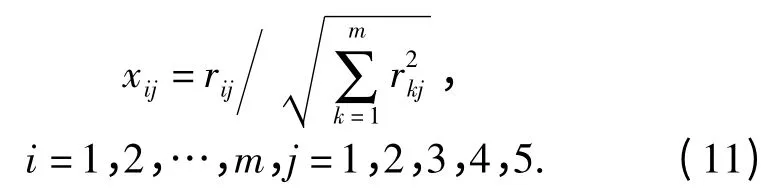
步骤2 建立加权归一化决策矩阵。决策过程往往受决策者主观偏好的影响，决策者的主观偏好通过权值向量引入到每个决策元素，权值向量w 形式如下:

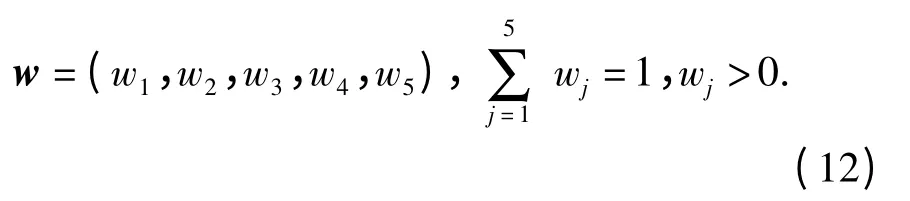
对步骤1 中得到的归一化决策矩阵的每个列向量乘其对应的权值wj，就得到加权归一化决策矩阵:

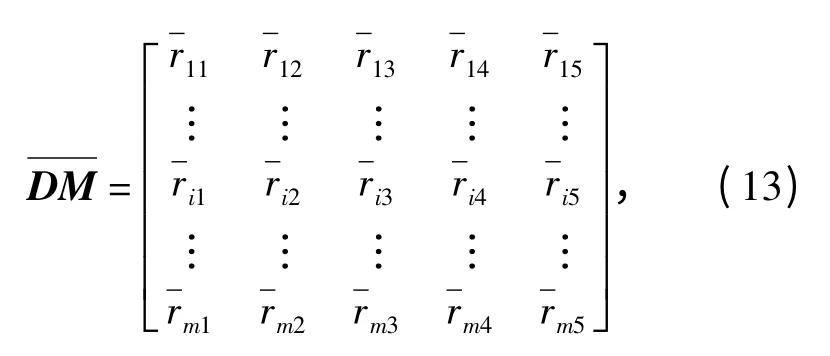
步骤3 确定IS 和NIS.IS 中A*对应的各决策准则使得系统性能最优，成本最低;而NIS 中A－对应的各决策准则使得系统性能最差，成本最高。对选定的5 个决策准则而言，参数值均是越小性能越好，成本越低;反之则性能越差，成本越高。对DM因为有因此

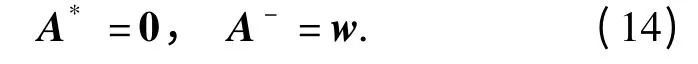
步骤4 计算各备选方案与IS 和NIS 之间的欧氏距离。备选方案与IS 的距离为

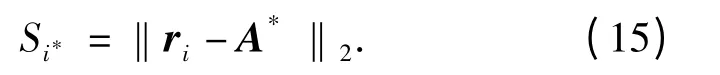
备选方案与NIS 的距离为

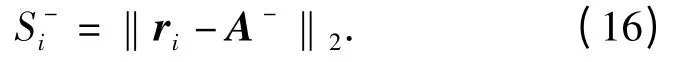
步骤5 计算备选方案与IS 的相对接近度。相对接近度定义为

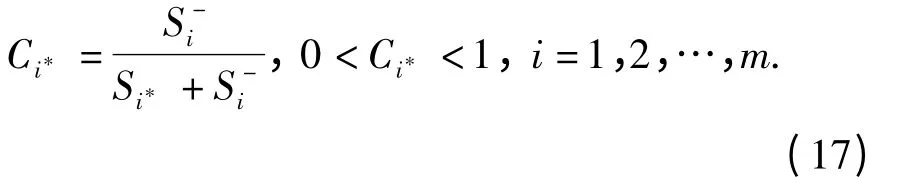
当Ci*=1 时，ri= A*;当Ci*=0 时，ri= A－.备选方案与A*越接近，Ci*越接近1.

步骤6 对每个备选方案所对应的Ci*值降序排列，得到备选方案的优先级排序。

3 设计参数备选方案及仿真

3.1 参数备选方案设计

设制导系统5 个设计参数的取值范围为:弹体时间常数TM取0.1 ～0.2 s;弹体阻尼比ξM取0.6 ～0.8;导引头延迟环节的延迟时间τ 取15 ～20 ms;导航比N 取4 ～8;导弹法向过载指令限幅nzm取40 ～50 g.

按照上述设定的取值范围，除导航比和弹体阻尼比取3 种值外，其余参数均取两种典型值，通过排列组合并去掉不合理参数组可得到34 组备选方案，每个方案的设计参数随方案编号的变化情况如图3 ～图7 所示。

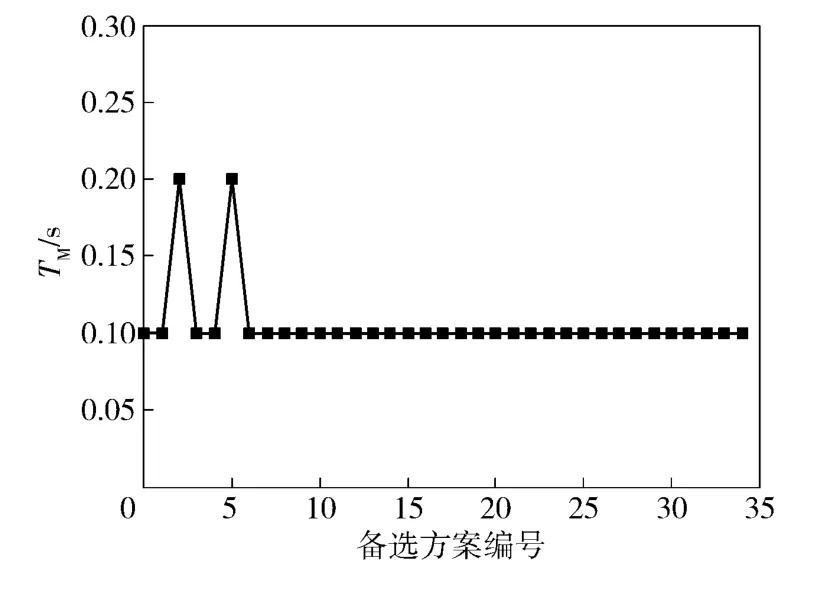
图3 导弹弹体时间常数方案Fig.3 Alternative for time constant of missile dynamics

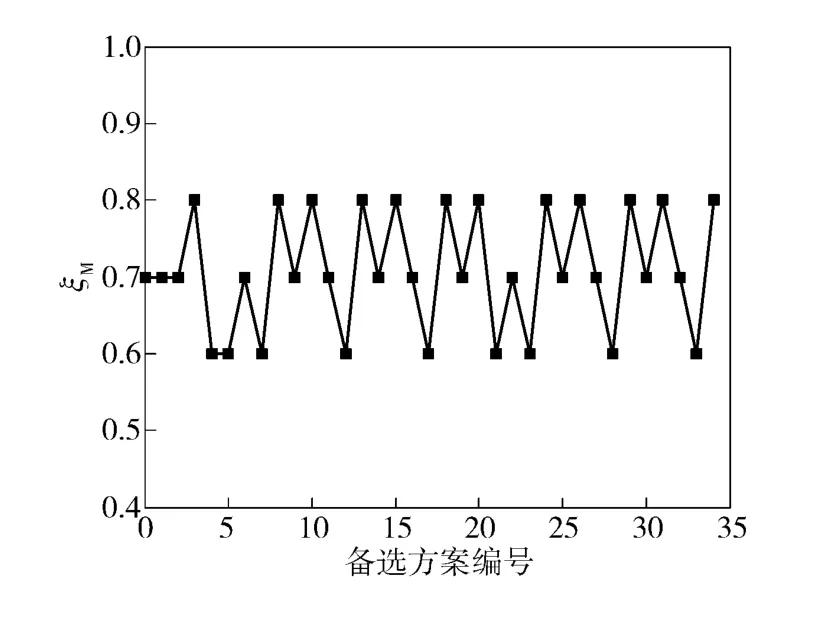
图4 导弹弹体阻尼比方案Fig.4 Alternative for damping ratio of missile dynamics

3.2 仿真条件设定

制导仿真中，取目标速度vT的Ma 数为1.2，目标机动加速度指令取幅值为9 g 的方波，角频率为0.5π rad/s.目标动力学特性参数ξT=0.7，TT=0.1 s.

导弹速度(Ma 数)取变速形式，表达式如下:

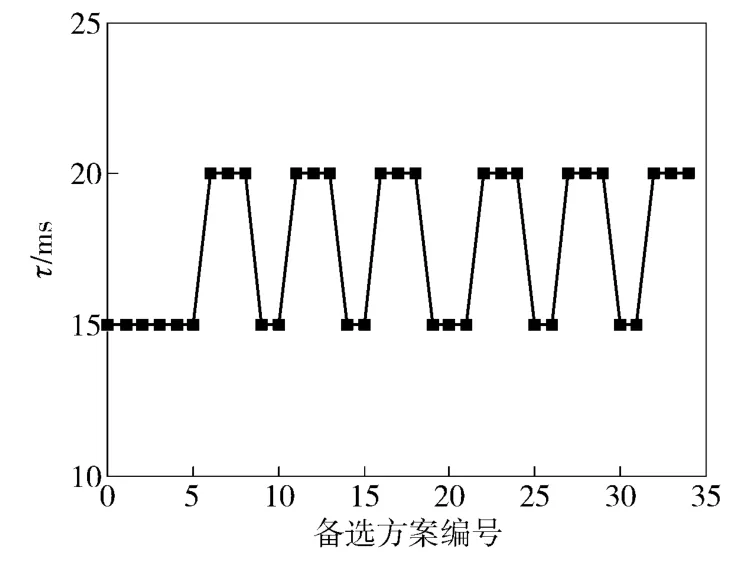
图5 导引头延迟时间方案Fig.5 Alternative for time delay of seeker

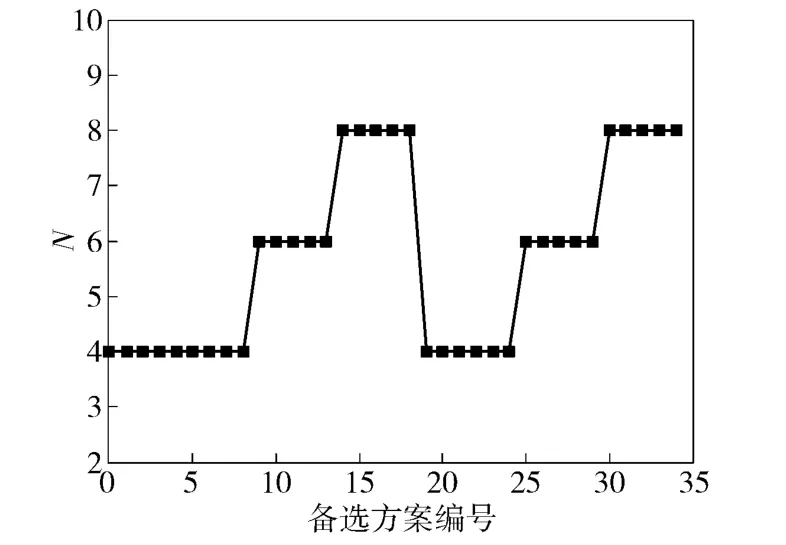
图6 比例导引导航比方案Fig.6 Alternative for navigation ratio of proportional navigation

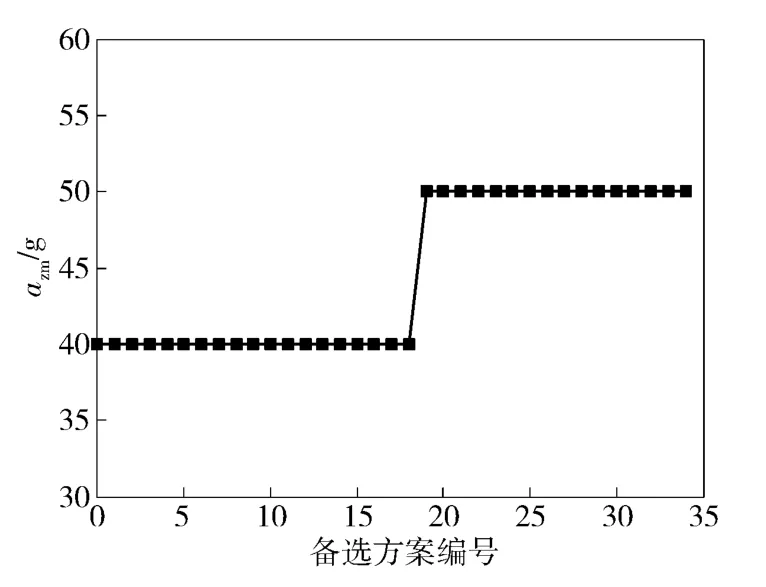
图7 法向过载限幅方案Fig.7 Alternative for maximum normal overload of missile

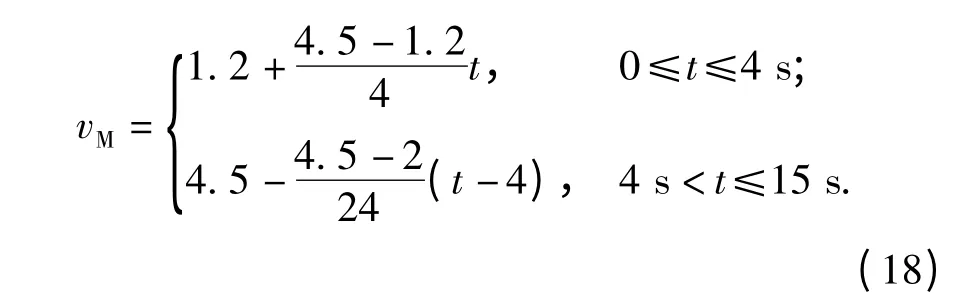
初始视线角固定取为q0=0°，导弹的初始速度倾角θM0取40°，目标初始航迹角θT0取0°、－30°和－120°三个值，弹目初始相对距离取6 000 m，这样一共有3 组初始条件，如表1 所示。

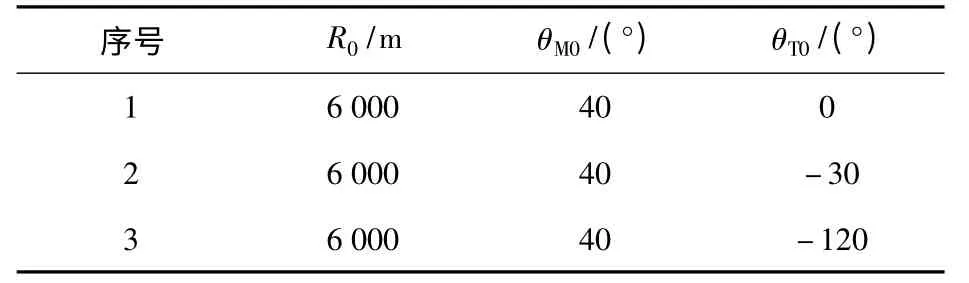
表1 仿真初始条件Tab.1 Initial conditions for simulation

3.3 备选方案脱靶量仿真结果

根据制导系统模型，仿真计算得到34 组备选方案在3 种初值下的脱靶量样本，脱靶量样本的均值和方差如图8 和图9 所示。

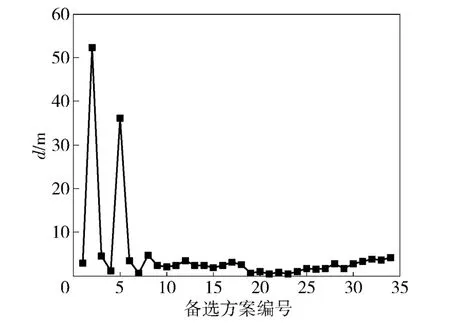
图8 备选方案脱靶量样本均值Fig.8 Mean value of miss distemces sample under different alternatives

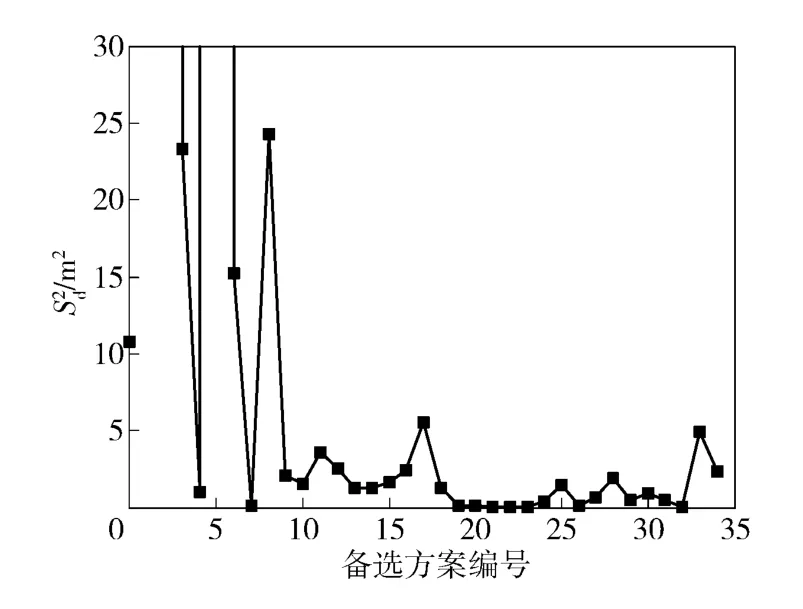
图9 备选方案脱靶量样本方差Fig.9 Variance of miss distance samples under diffidrent alternatives

4 设计方案决策与分析

根据前面给出的设计方案与仿真结果，(10)式DM 计算需要的全部信息已经得到，由此可计算出决策矩阵元素并进行归一化处理。

(12)式中权值向量w 的引入使得决策者能够根据不同的决策需求对各个决策准则重要性进行排序，使得决策方法具有较强的适用性。在实际应用中，w 的取值往往采用主观定性分析与客观定量分析相结合的方法确定。通常，决策者很难直接给出w 的具体取值，但根据需求给出各决策准则间的相对重要性是比较容易的。根据环比评分法的思想，两个决策准则对应的权值之比体现了他们之间的相对重要性[9]。因此，可以根据以下3 点原则，结合决策需求给出不同的权值向量w:

1)重要性高的决策准则对应的权值较大。权值越大，其对应准则对相对接近度的影响就越大，即该准则越重要。决策者可据此给出权值的大小关系;

2)两两比较决策准则间的相对重要性，确定权值两两之比，并根据约束条件，确定权值向量w;

依据以上原则，表2 给出了6 种不同的权值向量w 选择方法。表2 中，权值向量的取值从左到右代表了决策方式由性能优先到成本优先逐渐变化的过程。

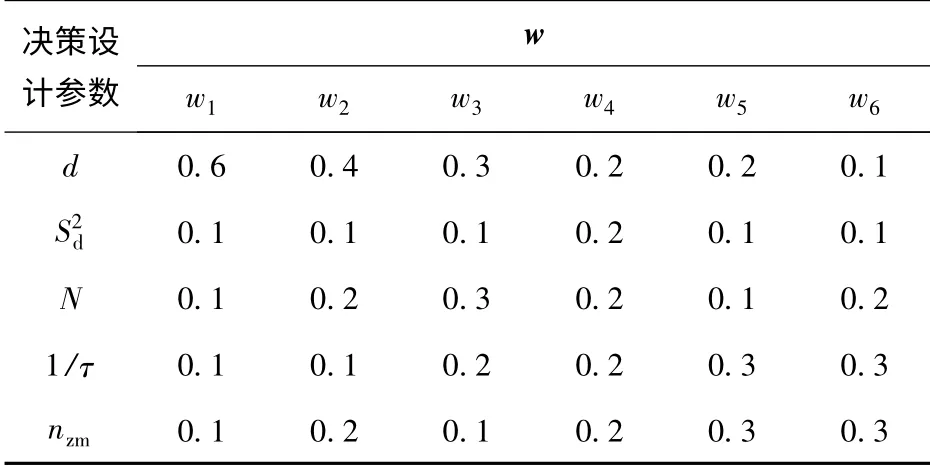
表2 权值向量取值Tab.2 Values of weight vectors

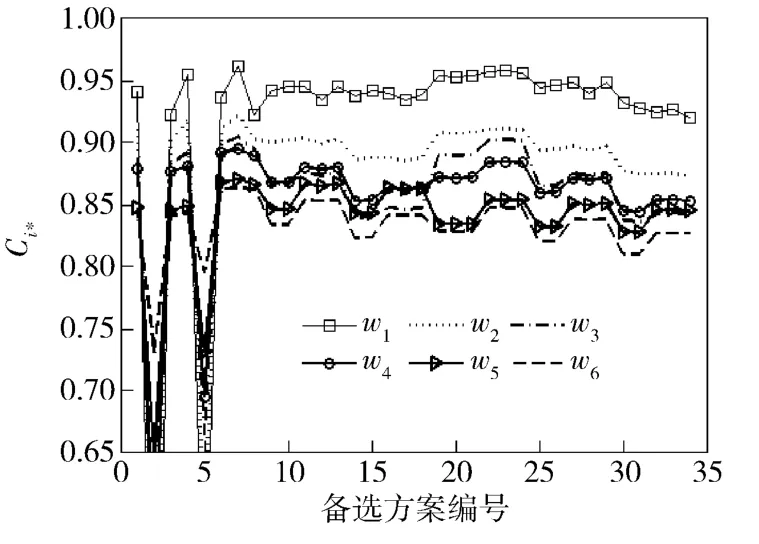
图10 不同权值方案相对接近度曲线Fig.10 Relative closeness under diffierent weighting schemes

根据归一化决策矩阵和表2 的权值向量，计算不同权值向量下备选方案的相对接近度Ci*见图10.按照6 种不同权值分别对Ci*进行降序排序，找出7 组具有典型意义的备选设计方案见表3.

由表3 可知，编号为4、6、7 和23 的备选方案基本能保持在较高的排位(前5 ～前10)，当成本指标1/τ 和nzm的权值增加时，编号为11 和13 的备选方案也进入排位前5，而编号为2 的备选方案一直排在最后一位。

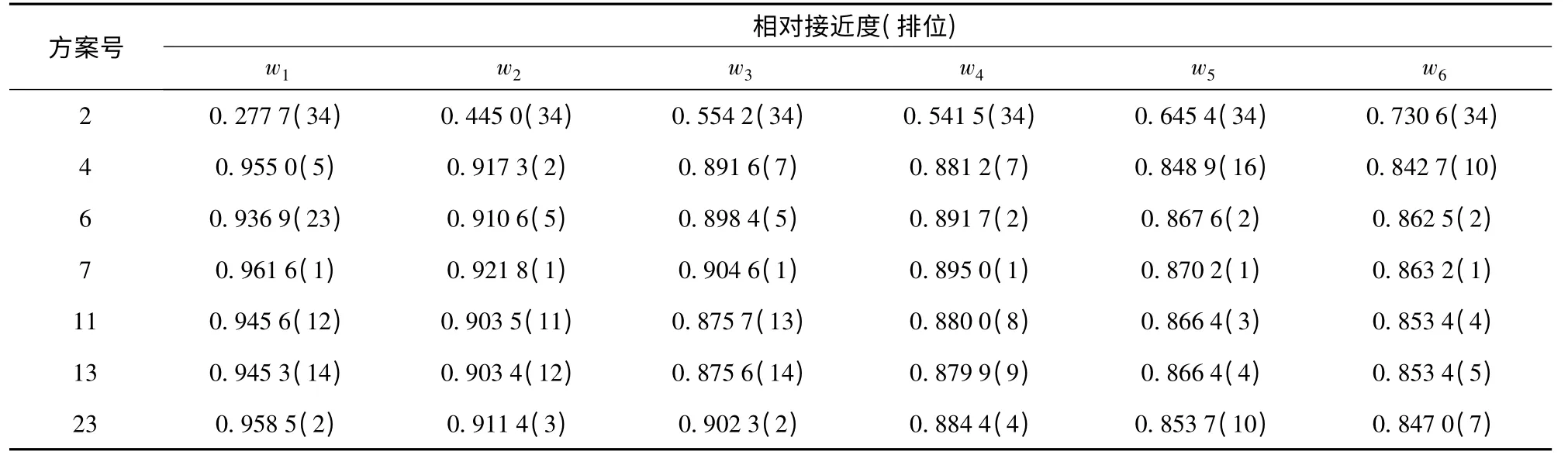
表3 典型备选方案相对接近度结果和排位Tab.3 Relative closeness and ranking of typical alternatives

结合图10 和表3 可以看出，在所有方案中备选方案7 均排位第一，而备选方案2 排位最末。依决策数据知，方案7 导引头延迟时间较大，弹体法向过载幅值较小，脱靶量均值及方差也很小，这说明方案7 属于成本较低、系统性能较高的方案。所以，不论决策者侧重性能还是成本，方案7 均能成为优先方案。相反，方案2 脱靶量均值远高于其他方案，成本准则也无优势，因此在每种排序结果中成为最差方案。虽然方案23 的性能准则d 和S2d优于方案7，但其法向过载幅值大，方案成本高。

应用TOPSIS 方法进行制导系统设计参数决策，能够有效排除不合理备选方案，决策出兼顾性能与成本等多项决策准则的设计方案。

5 结论

本文将导弹制导控制系统一体化设计参数决策问题转化为对系统设计参数的离散多准则决策问题，选取表征系统性能和成本等因素的多个指标作为决策准则，利用TOPSIS 方法对备选方案进行决策获得多准则优化方案。

利用本文的方法不但能够充分考虑制导系统的精度特性，而且能兼顾系统的成本因素等，对提高系统设计决策的最优性和鲁棒性十分有益。当然，对复杂的制导系统进行较为全面的参数准则决策需要大量的仿真分析和计算，但本文的方法和解决问题的思路无疑具有重要的参考意义。

References)

[1]雷虎民，刘文江，楼顺天.导弹稳定回路的一种简便自适应设计方法[J].西北工业大学学报，2002，20(2):306 －309.LEI Hu－min，LIU Wen－jiang，LOU Shun－tian.A simplified adaptive design method for the stable loop of missile[J].Journal of Northwestern Polytechnical University，2002，20(2):306 －309.(in Chinese)

[2]梁冰，徐殿国，段广仁.导弹俯仰通道带有落角约束的制导与控制一体化设计[J].科学技术与工程，2008，8(1):70 －75.LIANG Bing， XU Dian－guo， DUAN Guang－ren.Integrated guidance and control with terminal angular constraint for the missile’s pitch plane[J].Science Technology and Engineering，2008，8(1):70 －75.(in Chinese)

[3]Hwang C L，Yoon K.Multiple attribute decision making:methods and applications:a state－of－the－art survey[M].Berlin:Springer－Verlag，1981:186 －190.

[4]Andrew F，Brian G，Peter H，et al.DKM119 fast attack，air launched air to ground missile[R]∥The 1999 AIAA MSTC Graduate Missile Design Competition Request for Proposals.US:AIAA，1999.

[5]Kirby M R.A methodology for technology identification，evaluation，and selection in conceptual and preliminary aircraft design[D].Georgia:Georgia Institute of Technology，2001.

[6]Bandte O.A probabilistic multi－criteria decision making technique for conceptual and preliminary aerospace systems design [D].Georgia:Georgia Institute of Technology，2000.

[7]Bao Q，Ruan D，Shen Y，et al.Improved hierarchical fuzzy TOPSIS for road safety performance evaluation[J].Knowledge－Based Systems，2012，32:84 －90.

[8]Chen M S，Lin M C，Wang C C，et al.Using HCA and TOPSIS approaches in personal digital assistant menu－icon interface design[J].International Journal of Industrial Ergonomics，2009，39(5):689 －702.

[9]陆明生.多目标决策中的权系数[J].系统工程理论与实践，1986，6(4):77 －78.LU Ming－sheng.Weighting coefficient in multi－objective decision making[J].Systems Engineering－Theory ＆ Practice，1986，6(4):77 －78.(in Chinese)