车载防空导弹行进间发射过程动力学数值分析

钟洲，姜毅，刘群

(1.北京理工大学 宇航学院，北京100081;2.中国航天科工集团公司 二院 二部，北京100854)

0 引言

随着科技的发展，当今军事大国的侦察技术和精确打击力度逐渐提高，行进间发射能力已经成为车载防空导弹总体设计的一项重要指标。武器系统行进发射时导弹不仅受到弹射力影响，同时受到由于路面不平度激励造成的载车车体振动作用，这些因素严重影响了导弹的发射精度。

针对行进间发射问题，文献[1 －2]基于多刚体动力学理论的Kane－Huston 方法研究了自行火炮行进间射击的动力学问题，但是由于计算条件的较多简化处理并且忽略了结构件的柔性效应，计算精度不高。本文使用多体动力学软件搭建了车载防空导弹的刚柔耦合动力学模型，分别对随机路面上的行驶动力学和行进间发射动力学进行了完整动态特性模拟，获得了战车的振动响应和导弹的姿态参数。根据战车行进间振动特性，分析了车载防空导弹以3 种车速在B、C 等级路面工况行进下的发射精度，保证了发射任务的安全性。

1 路面不平度

国内外许多测量分析表明，作为车辆振动输入的路面不平度是具有零均值，各态历经平稳Gauss随机过程[3－4]。国际标准协会在文件ISO/TC108/SC2N67 中提出的《路面不平度表示方法草案》中，建议路面功率谱密度函数用下式作为拟合式[5]:

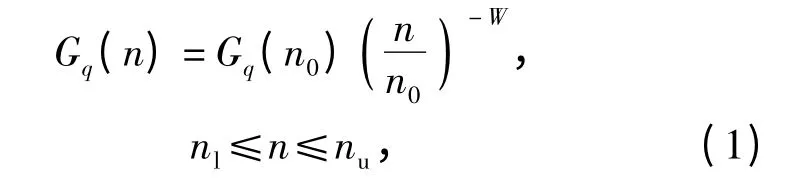
式中:n 为空间频率;nl和nu分别表示路面谱的上、下限空间频率;n0为参考空间频率，n0=0.1 m－1;W为决定路面谱频率结构的频率指数，取W = 2;Gq(n0)为路面不平度系数，根据《GB/T 7031—2005机械振动 道路路面谱测量数据报告》，B 级路面为64 mm2/m－1，C 级路面为256 mm2/m－1.

针对路面不平度的数值模拟问题，本文使用自回归(AR)模型的方法。AR 系统相当于一组数字滤波器，将白噪声变成近似具有目标谱密度或相关函数的离散随机场。设空间路面不平度用随机过程q(k)表示，满足以下AR 模型:

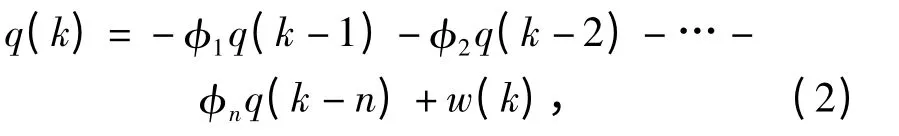
根据空间域平稳过程q(k)的自相关函数Rq(τ)的性质，可以得到k 阶AR 模型的Yule－Walker 方程为

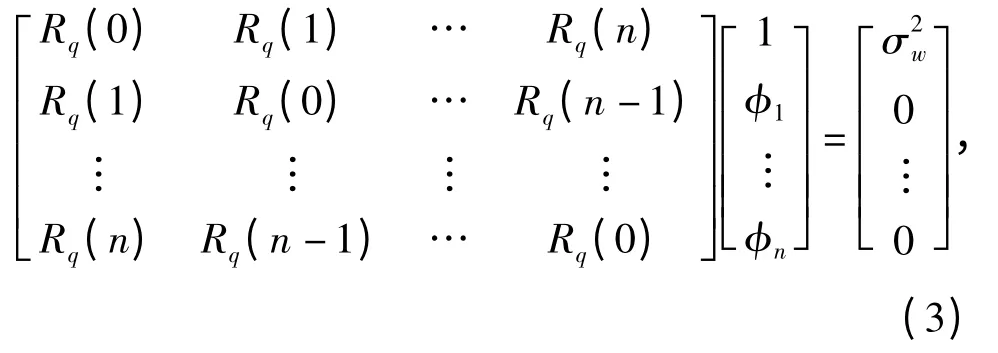
式中:自相关函数公式为

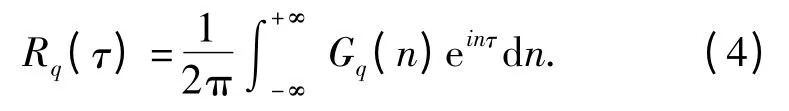
联合(1)式～(4)式，可求解得AR 模型的参数φi(i=1，2，…n)和σ2w.

路面模型的距离采样间隔Δl 和采样阶数n 对AR 模型的精确性和稳定性有重要的影响。若采样点数为N，则采样距离为L =NΔl，空间频率分辨率为Δn =1/L，为避免频率混叠和保证仿真模型的有效空间频率下限nl准确，应满足:

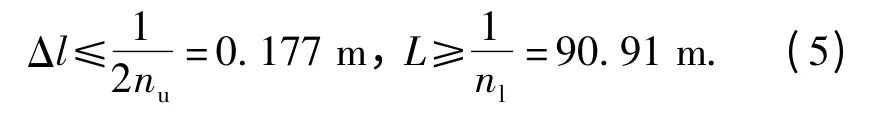
同时，对于采样阶数n 的选择，采取最小信息准则(AIC)进行最优判断，计算公式定义为

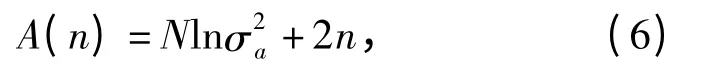
式中:A 为AIC(n)准则;σa是残差方差，

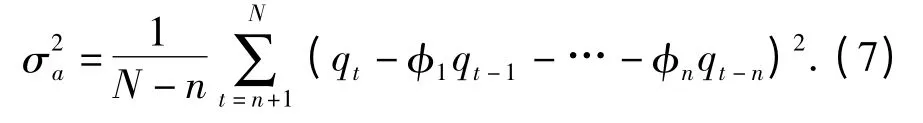
设定最高阶数25，按阶数从小到大的顺序使用Matlab 软件对B、C 级路面进行仿真建模，模拟频率范围为0.011 ～2.83 m－1，采样间隔为0.1 m，采样次数为1 000 次，这样可以得到各阶模型下能够形成100 m 长度路面的数据点，分别计算各模型的A(n)，取值最小时的n 作为最佳阶数。经计算对比，本文的AR 模型阶数定为20.图1 为仿真所得C 级路面不平度曲线，根据周期图法估计，将生成路面的功率谱密度与理论功率谱密度对比，如图2 所示。功率谱密度图采用双对数坐标，由图可知，仿真路面有着较高拟合精度。

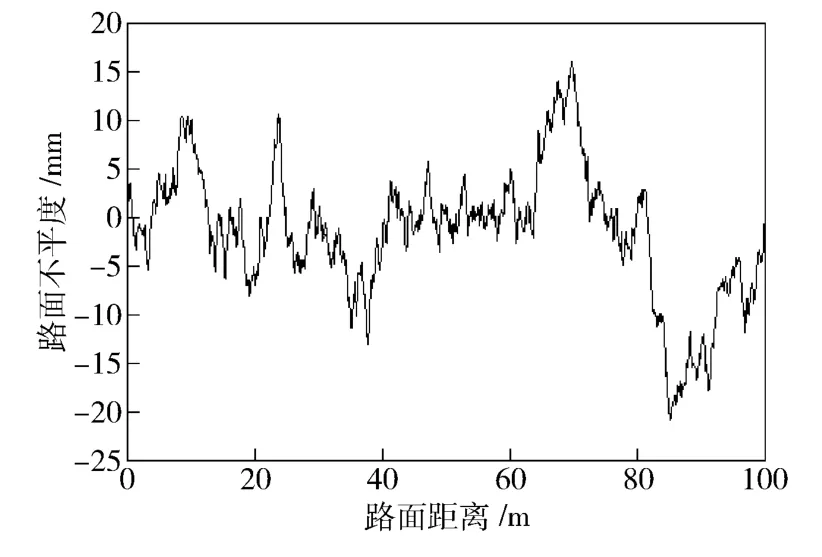
图1 C 级路面不平度曲线Fig.1 Roughness curve of C－grade road

2 行进间发射动力学仿真建模

2.1 武器系统组成分析与假设

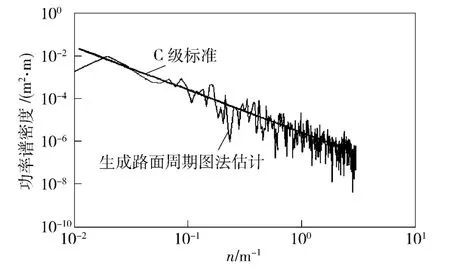
图2 路面谱验证Fig.2 The verification of road spectrum

根据武器系统的子部件功能关系，武器系统分为载车和上装发射装置。上装发射装置通过支架和支撑杆固定在车体，包括弹射装置，发射箱，导弹，导轨和闭锁机构等，系统主要部分拓扑连接为图3 所示。考虑到系统各结构特性对发射过程的影响程度，本文将底盘，支架、支撑杆和弹体作为柔性体。利用有限元软件对欲处理成柔性体的构件实体模型进行网格划分，定义好附着点(施加力与约束副的外部节点)和构件间实际连接处节点的关系，通过宏命令得到模态中性文件，导入机械系统动力学自动分析(ADANS)生成柔性体，共有72 个附着点和1 324 578个节点数。

车载防空导弹行进间发射时的力学环境非常复杂，为了描述武器系统在行进间发射时的动力学特性，特作如下假设:

1)不考虑连接铰的间隙，均设为理想约束;

2)悬挂系统简化成旋转或平移的弹性元件，利用线性和非线性曲线描述其刚度和阻尼特性(仿真中利用Vforce 力元模拟);

3)不考虑发射过程中导弹的变质量特性。

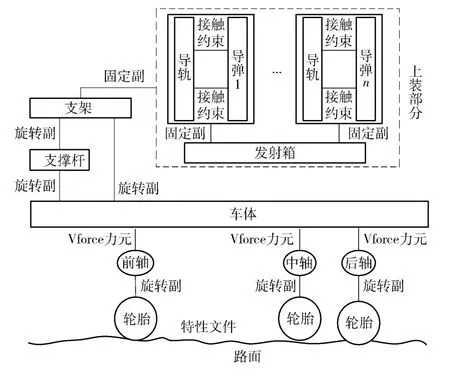
图3 拓扑连接图Fig.3 Topological connection graph

2.2 轮胎路面模型

轮胎选择FTire 模型[6－7]，其本质是柔性环模型，能描述胎内振动和胎外特性;胎体在圆周方向离散成多个单元，相互之间以弹簧连接，轮辋和胎体以三向弹簧相连，弹簧刚度与轮胎转速相关;橡胶轮胎的表面摩擦系数是一个与压力和滑移速度相关的函数。Ftire 模型的这些特点能很好地仿真轮胎复杂的非线性特性，同时Ftire 模型不需要对路面数据做预处理，可用于短波不平路面，甚至存在高或锋利的障碍物路面。建立该模型需要轮胎具体几何参数、质量属性、静刚度和模态参数等。

将轮胎相关的各参数试验数据写入轮胎文件和多次仿真获取的路面不平度数据写入路面谱文件，通过ADAMS 系统中Tire 模块导入可以生成相应轮胎路面模型。

2.3 激励

车辆行驶驱动力由发动机提供，仿真通过对车体和主动轮间施加驱动力矩来模拟车体匀速运动，驱动力矩在时间t 内先由0 增至Mmax，让车体加速到所需速度，然后瞬时降至Mmax－ΔM，达到受力平衡状态，此后匀速行驶。驱动力矩拟合函数为step(time，0，0，t，Mmax)+ step(time，t，0，t +0.001，－ΔM).

由于导弹发射采用冷发射方式，发射过程导弹所受主要激励为弹射力，闭锁挡弹器的闭锁力以及导弹定向钮与导轨的接触碰撞力。其中闭锁力的效果采用传感器激发，当弹射力大于闭锁力时开始让导弹解锁运动;由于弹体为柔性体，发射过程中的接触碰撞作用利用Flex body to solid contact 约束，其参数值与接触材料有关，可根据试验数据和软件提供的经验数据设定;弹射力由提拉杆式弹射装置提供，采用随体单向力模拟该载荷，作用点位于提弹梁质心，方向近似平行于导轨，载荷大小为

式中:p(t)为试验测量所得各时刻燃气压强;S 为活塞筒截面积，采用AKISPL 函数拟合。

2.4 整车刚柔模型

整个系统模型由路面激励、轮胎、车轴、悬挂系统、发射箱、导轨和14 个柔性体组成，共有314 个自由度。图4 为按照图3 所示拓扑连接建立的刚柔耦合动力学模型，系统的惯性坐标系如图中所示。

3 仿真结果与分析

3.1 行驶动力学仿真分析

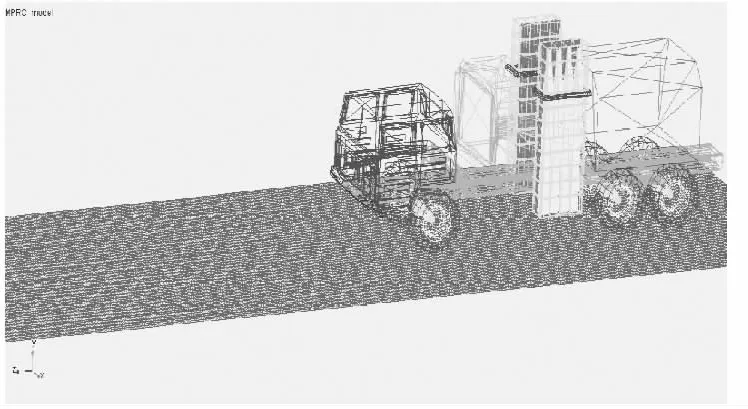
图4 刚柔耦合模型Fig.4 Rigid－flexible coupling model

由图4 所示车载防空导弹系统离散模型可知，导弹发射箱垂直装置在车体左右两侧。为了凸显发射的更恶劣工况，模型中弹装载情况为左侧发射箱弹满载，右侧空载。受路面不平度激励和不同车速行进发射时刻不同的影响，会形成导弹发射的初始条件不同，为了分析行进间导弹的发射精度，需要先通过行驶动力学仿真找出极限发射时刻。

本文根据建立的多柔体模型，完成了行驶动力学仿真。武器系统先在足够长度的仿真路面上进行静平衡，然后由车速0 加速至行驶速度，接着车辆以稳定车速行驶，整个仿真过程持续20 s.图5 和图6分别为相同车速、不同路面和不同车速、相同路面上的车体质心垂直振动位移;图7 为其中一种工况下(25 km/h 车速，C 级路面)的车体侧倾角时间历程曲线。

由图5 和图6 可知，防空导弹发射车的振动随着路况好坏和车速的改变，曲线峰值反映出相应的变化。C 级路面造成的最大振动幅度比B 级工况大了7 mm;30 km/h 行驶速度下引起的最大振动幅度比20 km/h 工况大了11 mm，增加了将近90%.考虑到随机路面的偶然性，表1 列出了车体垂直振动位移的均方根值随车速和路面等级的变化情况，可见，为了改善车体振动响应，路况越糟糕，行驶速度越应该得到控制。

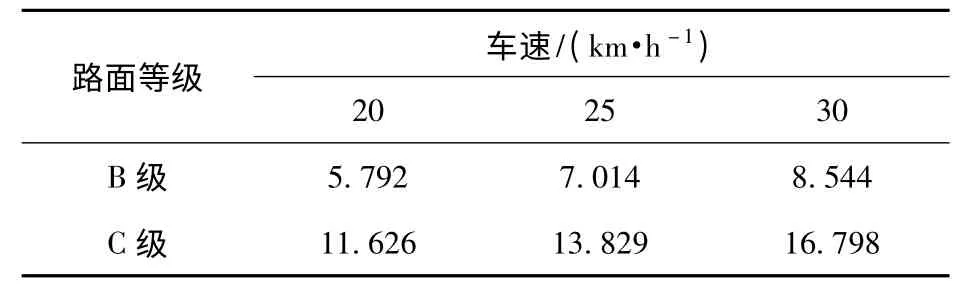
表1 车体垂直振动位移均方根值Tab.1 Root mean square value of vehicle vertical displacement mm

由图7 可看出，随机路面激励使车体在20 s 的行驶过程中呈现出多次幅度不同的摇摆震荡运动。由于测量坐标系和系统惯性坐标系一致且弹装载情况仅为左箱满载，根据图4 中的系统惯性坐标系可知，此工况下的极限发射时刻确定为车体侧倾角负向绝对值最大处，即图中标示的13.1 s，此时侧倾角绝对值为2.13°.

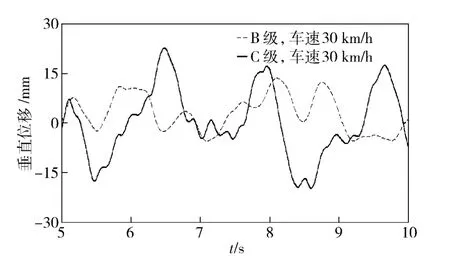
图5 不同路面上车体垂直振动位移Fig.5 Vehicle vertical displacement in different road conditions

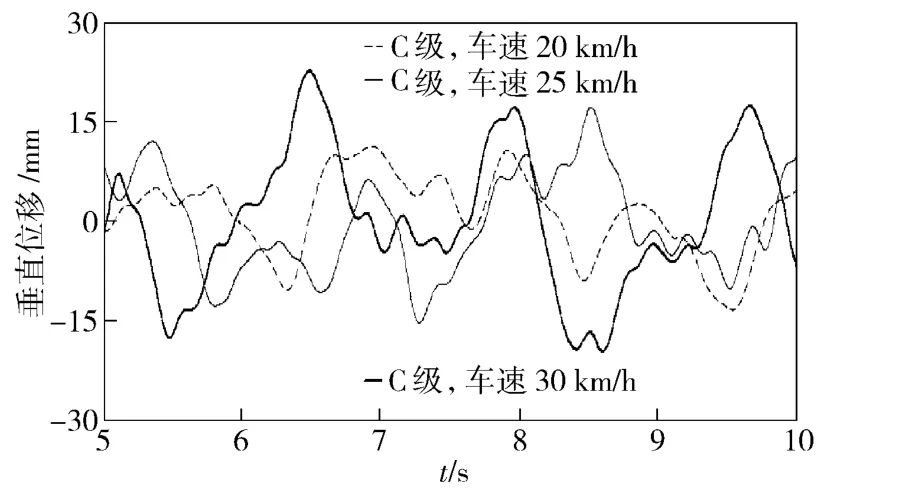
图6 不同速度下车体垂直振动位移Fig.6 Vehicle vertical displacement at different speeds

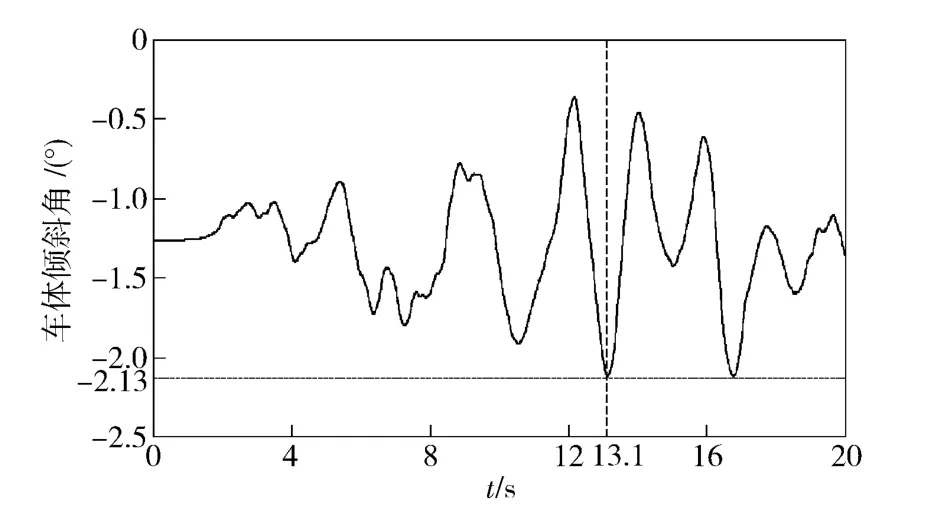
图7 车辆25 km/h 时的车体侧倾角Fig.7 Vehicle roll angle at 25 km/h

3.2 行进发射动力学仿真分析

根据行驶动力学仿真分析结果，通过传感器设置好导弹发射时刻，进行行进发射动力学仿真。受篇幅所限，仿真后处理中各项测量时间历程曲线不予罗列，仅提供主要的具体离轨时刻数据。6 种工况下极限发射时刻、对应车体侧倾角、导弹出筒时刻姿态和发射过程中导弹姿态均方根值如表2 所示。

由表2 中极限发射时刻和导弹姿态均方根值变化可看出，由于路面激励的随机性，引起的车体振动情况不一致，发射时刻也表现出随机特征，需要具体工况具体分析;车速和路况对导弹滚转姿态影响规律不明显，因为滚转姿态还直接受到弹箱结构和装配特征影响，但是，对于决定起控精度的俯仰和偏航姿态而言，其数值随着路况越差和车速越高显现出显著增大的趋势，可见二者都起着重要影响;其中车速影响程度较大，这是由于随着车速提高，车体振动加剧，当外力激励频率接近于武器系统固有频率时，能引起共振，放大了来自于路面不平度的激励作用。

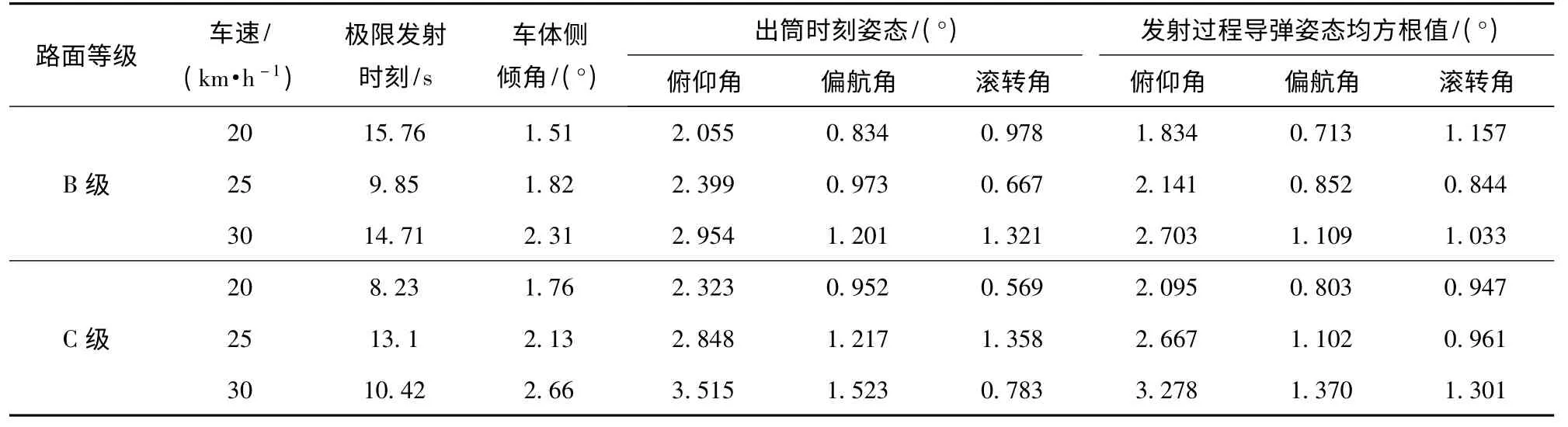
表2 导弹姿态Tab.2 Missile attitude

依据相关制导要求，对比仿真结果中出筒时刻姿态数据，可以对不同路况和车速行进间发射安全性做出有效的参考结论。

4 结论

1)利用AR 方法可以完成具有较高精度的路面不平度仿真模拟;基于多柔体动力学理论，在虚拟样机平台上建立的车载防空导弹行驶和行进发射动力学模型是高效的，对武器系统设计具有参考价值。

2)结合武器系统行驶和行进间发射动力学仿真，可以完成导弹发射精度分析，保证导弹发射安全性。仿真结果表明，路面质量越差，车体的振动就越大，造成导弹发射时的初始条件也越恶劣，导致内弹道结束后导弹的离轨姿态偏差越大，影响发射安全可靠性;相同路况时，发射车行驶速度越高，导弹发射和起控精度也越低。因此，要保证行进间发射精度，不同路况下有最高车速限制。

3)基于本模型假设和最大3.5°的出筒姿态设计指标要求，武器系统在B 级路面上以3 种速度行进发射时，导弹离轨参数都在要求制导范围内，能安全完成发射任务。但是，在C 级路面下车速受限于25 km/h.

References)

[1]冯长根，温波，李才葆.自行火炮行进间射击动力学研究[J].兵工学报，2002，23(4):407 －410.FENG Chang－gen，WEN Bo，LI Cai－bao.Dynamic analysis of a self－propelled gun firing on the move[J].Acta Armamentarii，2002，23(4):407 －410.(in Chinese)

[2]闵建平，谭俊杰，李剑锋.行进间射击时的动力学研究[J].振动与冲击，2003，22(4):88 －92.MIN Jian－ping，TAN Jun－jie，LI Jian－feng.Study on dynamics of self－propelled guns at firing on the move[J].Journal of Vibration and Shock，2003，22(4):88 －92.(in Chinese)

[3]金睿臣，宋健.路面不平度的模拟和汽车非线性随机振动的研究[J].清华大学学报:自然科学版，1999，39(8):76 －79.JIN Rui－chen，SONG Jian.Simulation of road irregularity and study of nonlinear random vibration of the automobile[J].Journal of Tsinghua University:Science and Technology，1999，39(8):76 －79.(in Chinese)

[4]Schiehlen W，Hu B.Spectral simulation and shock absorber identification[J].International Journal of Non－Linear Mechanics，2003，38(2):161 －171.

[5]余志生.汽车理论[M].北京:机械工业出版社，2006.YU Zhi－sheng.The theory of automobile[M].Beijing:China Machine Press，2006.(in Chinese)

[6]MSC Software.ADAMS 2007r1/help:ADAMS/Tire[G].US:MSC Software，2007.

[7]Gipser M.FTire_2008[R].Germany:Esslingen University of Applied Sciences，2008.